2次元電位分布の数値計算
概要 †
与えられた境界条件を満たす2次元電位分布を数値計算により求めたい。
基礎方程式 †
電位決定の基礎方程式 †
物質中におけるマクスウェル方程式において
を仮定すれば、
(*)
第1式より電位の存在が導かれ、
とともに第3式に代入すれば、
特に、真電荷のない領域では
これが基礎方程式となる。
電場の z 成分がゼロのとき 、成分に分けて書けば
媒質が等方的 ( ) かつ 均質 ( ) であれば、
いわゆるポアソン方程式( ならラプラス方程式)に帰着する。
シート状伝導体における基礎方程式 †
(*) 式の第2、第3式から電荷保存則
が導かれる。
定常状態では より、
ここにシート状伝導体におけるオームの法則
電場と電位の関係式
を代入すると、
これがシート状伝導体における電位の基礎方程式となる。
成分に分けて書けば、
こちらも、コンダクタンスが等方的かつ一様であればポアソン方程式になる。
中心軸対称な電場分布に対する円柱座標の基礎方程式 †
基礎方程式
を円柱座標
で書き表すと、
より、
この場合には第1項の中に現れる r のため、単純なポアソン方程式にはならず、 方程式は座標 r に依存する
ラプラス方程式を差分方程式に直す †
2次元空間を を単位として格子状に分けて、
とする。 が十分に小さい時、
などが成り立つことを利用すると、ラプラス方程式を差分方程式に直すことができて、
を得る。
つまり、この差分方程式を満たすような は、元の方程式の近似的な解となる。
ヤコビ法 †
前項の最後に得た式を漸化式に置き換える。すなわち、
何らかの方法により試行的な電位分布 を定め、 上記の漸化式で分布を更新していった結果、もしこれが に収束したならば、
が成り立ち、この収束値が近似的に求めた電場分布を与えることになる。
このような手法はヤコビ法と呼ばれ、 の係数が比較的大きい場合にはよく収束することが知られている。
LANG:C
double calc_new_value(double t, double r, double b, double l)
{
return 0.25 * (t + r + b + l); // Laplace
}
参考:https://ja.wikipedia.org/wiki/%E3%83%A4%E3%82%B3%E3%83%93%E6%B3%95
1つ飛ばしのヤコビ法 †
上記の漸化式では はその上下左右の4つの格子点に依存しているが、 その他の点には依存していない。
すなわち、このような格子を考えれば、
赤いマスは白いマスに、白いマスは赤いマスにしか依存していない。
そこで、すべての格子点を一度に漸化式にかけるのではなく、 赤いマスと白いマスと交互に漸化式で更新してやれば、 回目と 回目とに別々の記憶領域を取る必要がなくなる。
しかも恐らく、普通の2倍くらいの収束速度が得られそう???
境界条件 †
領域の端では などが領域外に出てしまうため、 何か条件を定めないと計算ができない。
領域の端を固定端とするには、領域外の値としてその固定値を入れてやれば良い。
領域の端を自由端とするには、領域外の値として と同じ値を入れてやれば、 などの条件を満たすことができる。
収束条件 †
更新前と後とを比べて、変化が小さくなれば収束したと見なす。
具体的には、もっとも変化の大きかった格子点での変化量が規定値を下回れば収束したことにする。
もっといい方法があるかもしれないけれど、とりあえず、これで。
加速・減速 †
通常のヤコビ法に比べて収束を早くしたければ、
LANG:c new_value = calc_new_value(); new_value = old_value + (new_value - old_value) * speed;
のように、変化量を線形に増加 (1 < speed) させたり、減少 (0 < speed < 1) させたりすることも効果がある場合がある。
計算手法上は上記のままでは new_value - old_value の部分で桁落ちが心配されるため、
LANG:c new_value = calc_new_value(); new_value = (1-speed) * old_value + speed * new_value;
と計算する方が良い。
このような方法を SOR 法と呼ぶ。https://ja.wikipedia.org/wiki/SOR%E6%B3%95
- 加速させると、うまく行けば収束が速くなるが、発散しやすくなる。
- 減速させると、通常のヤコビ法 (speed = 1) では発散してしまう場合にも解を得られる可能性がある。
コードの概要 †
LANG:C
// n x n の正方領域を考える
// even_or_odd = 1 or 0 が与えられる
// pixel(p,q) で現在の値を得る
// set_pixel(p,q,v) で値を更新する
// mask(p,q) で固定端を判別する
// 更新差分の相対値の最大値を diff に残す
double half_step(int even_or_odd)
{
int p, q, nm1 = n-1;
int pstart = 1 + (even_or_odd ^ (q % 2));
double result = 0;
for(q = 1; q < nm1; q += 1 ){
for(p = pstart; p < nm1; p += 2 ){
if(mask(p, q)) continue; // 固定端は更新しない
double value = pixel(p, q);
if(isnan(value)) continue; // 自由端も更新しない
double new_value = calc_new_value(
replace_nan(pixel(p , q-1), value),
replace_nan(pixel(p+1, q ), value),
replace_nan(pixel(p , q+1), value),
replace_nan(pixel(p-1, q ), value)
);
// 速度を調整しつつ値を更新
set_pixel(p, q, (1-speed) * value + speed * new_value);
// 変化量を記録
double diff = fabs(new_value-value);
if( !isnan(diff) && diff > result ) result = diff;
}
}
return result;
}
double replace_nan(double value, double replace)
{
return isnan(value) ? replace : value;
}
徐々に粒度を上げる †
精確な電位を求めるには格子間隔 を小さくするのが望ましいけれど、 初めから小さくすると精確な解が得られるまでに多大な時間がかかってしまう。
そこで、細かい粒度で計算を始めるにあたり、粗い粒度で計算した結果を初期値として使うのが賢いやり方になる。
すなわち、まず粗い粒度で計算しておいて、徐々に粒度を上げていくのである。
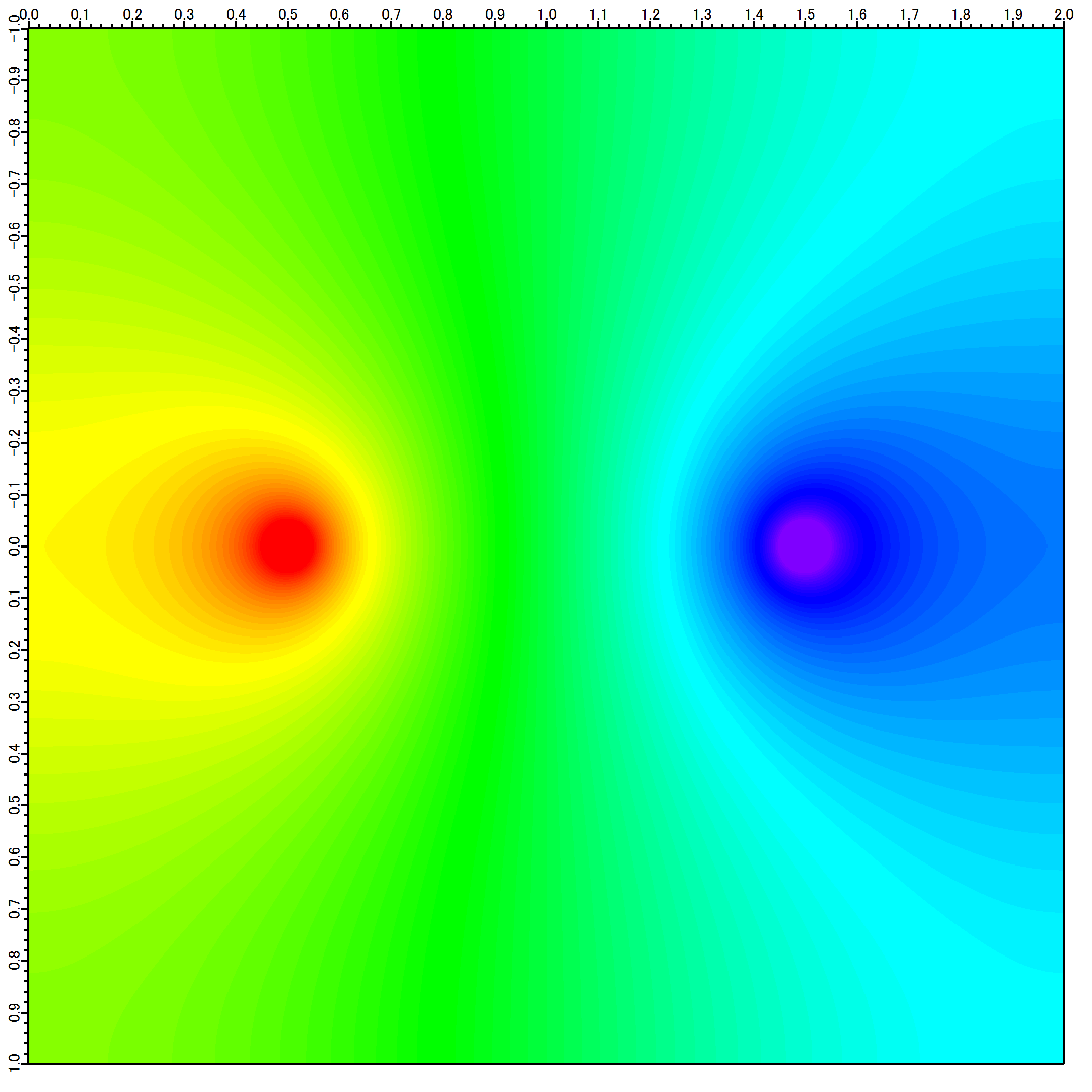
例:一様な抵抗を持つ2次元伝導体への電流注入 †
- 計算領域は x, y ともに±1の範囲 = 一辺2の正方領域
- (±0.5, 0.0) を中心に、半径0.05の円形領域から電流を注入した
- 電位を±1とした
33pixel †
65pixel †
129pixel †
257pixel †
計算ライブラリ †
計算効率はあまり追求しない方針で。
pdesolver2d.h †
LANG:cpp
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <memory.h>
#include <float.h>
#include <algorithm>
#include <time.h>
#include <signal.h>
#ifndef __PDESOLVER2D
#define __PDESOLVER2D
// 2D正方領域で偏微分方程式 (PDE: Partial Differential Equation) を
// 解くためのクラス
//
// 領域サイズは n ピクセル x n ピクセル
// pixel に NaN を書き込むと、そこは自由端になる
// mask に非ゼロを書き込むと、そこは固定端になる
// 領域の周囲は必ず自由端もしくは固定端にしておかなければならない
//
// PDESolver2D 自体は抽象クラスなので、子クラスにて calc_new_value
// を実装して、周囲4点の値から新しい値を求める漸化式を与えないと
// 実体化できない
//
class PDESolver2D
{
protected:
int n;
double *pixels; // NaN を代入すると自由端になる
int *masks; // 非ゼロを代入すると固定端になる
int interrupted; // 強制終了する
double speed; // 加速、減速定数 (speed > 1 で加速)
public:
PDESolver2D(int n); // n x n の正方領域を確保する
virtual ~PDESolver2D();
int size() { return n; }
double pixel(int p, int q)
{ return pixels[n*q+p]; }
void pixel(int p, int q, double v)
{ pixels[n*q+p] = v; }
int mask(int p, int q)
{ return masks[n*q+p]; }
void mask(int p, int q, int v)
{ masks[n*q+p] = v; }
void clear() { memset(pixels, 0, n*n*sizeof(double));
memset(masks, 0, n*n*sizeof(int)); }
void interrupt(){ interrupted = 1; }
void set_speed(double s) { speed = s; }
// 全ピクセルで更新差分の相対値が delta 未満になるまで繰り返し計算する
// 更新差分の相対値とは更新差分をピクセル値で割った値のこと
// 計算が終了すれば非ゼロを返す
// 途中でキャンセルされればゼロを返す
// log がゼロでなければ stderr に表示する進行状況を log にも出力する
int solve(double delta, FILE *log = NULL);
// 指定されたファイルにデータを書き込む
void dump(const char *file_name);
// 現在の計算値を引き継いで2倍の解像度の領域を確保する
virtual PDESolver2D *create_double(int delete_this = 0);
protected: // 子クラスで実装すべき virtual 関数
// 自身の値 (c) と上下左右 (t, b, l, r) と座標値 (p,q) より、新しい値を計算して返す
virtual double calc_new_value(double c, double t, double r, double b, double l, int p, int q) = 0;
// サイズ n のインスタンスを作成して返す
virtual PDESolver2D *create_instance(int n) = 0;
protected: // 内部で用いるヘルパー関数
// create_double 内から呼ばれる。2倍領域のピクセル座標を
// 元画像に与えると、元画像のピクセル値を補完した値を返す
double interpolate(int p, int q);
// 自由端処理のためのヘルパー関数
double replace_nan(double value, double replace)
{ return isnan(value) ? replace : value; }
double replace_nan(int p, int q, double replace)
{ return replace_nan(pixel(p, q), replace); }
// 進行状況を表示する
void log_step(int i, double diff, time_t started_at, FILE *log);
// 奇数ピクセルあるいは偶数ピクセルだけを計算する
// ピクセル値の更新差分の相対値の最大値を返す
double half_step(int even_or_odd);
// 計算を1回分進める
// 内部では half_step を2回呼ぶ
// ピクセル値の更新差分の相対値の最大値を返す
double step();
};
#endif
pdesolver2d.cpp †
LANG:cpp
#include "pdesolver2d.h"
PDESolver2D::PDESolver2D(int n)
{
speed = 1;
this->n = n;
interrupted = 0;
pixels = new double[n*n];
masks = new int[n*n];
clear();
}
PDESolver2D::~PDESolver2D()
{
delete pixels;
delete masks;
}
int PDESolver2D::solve(double delta, FILE *log)
{
time_t started_at = time(NULL);
int i;
double diff = -1;
int how_often = 53;
for(i = 1; !interrupted; i++) {
diff = step();
if(log && (i % how_often == 0))
log_step(i, diff, started_at, log);
if(diff < delta) break;
}
if(log) log_step(i, diff, started_at, log);
return !interrupted;
}
void PDESolver2D::log_step(int i, double diff, time_t started_at, FILE *log)
{
if(log!=stderr)
fprintf(log, "step (%6d, %e, %5.1fs)\n", i, diff, difftime(time(NULL), started_at));
fprintf(stderr, "step (%6d, %e, %5.1fs)\r", i, diff, difftime(time(NULL), started_at));
}
double PDESolver2D::half_step(int even_or_odd)
{
int p, q, nm1 = n-1;
double result = 0;
for(q = 1; q < nm1; q += 1 ){
for(p = 1 + (even_or_odd ^ (q % 2)); p < nm1; p += 2 ){
if(mask(p, q)) continue; // 固定端
double value = pixel(p, q);
if(isnan(value)) continue; // 自由端
double new_value = calc_new_value(
value,
replace_nan(p , q-1, value),
replace_nan(p+1, q , value),
replace_nan(p , q+1, value),
replace_nan(p-1, q , value),
p, q
);
pixel(p, q, value + speed * (new_value-value));
double diff = fabs(new_value-value)/(fabs(new_value)+fabs(value));
if( !isnan(diff) && diff > result ) result = diff;
}
}
return result;
}
double PDESolver2D::step()
{
return std::max( half_step(0), half_step(1) );
}
PDESolver2D *PDESolver2D::create_double(int delete_this)
{
int p, q;
PDESolver2D *result = create_instance(2*(n-1)+1);
for(p = 0; p < result->size(); p++){
for(q = 0; q < result->size(); q++){
result->pixel(p, q, interpolate(p, q));
}
}
if(delete_this) delete this;
return result;
}
double PDESolver2D::interpolate(int p, int q)
{
double i = 0;
double result = 0, pix;
int p2 = p/2, q2 = q/2;
if(p % 2){ // need interpolation for p
if(q % 2){ // need interpolation for q
if (!isnan(pix = pixel(p2 , q2 )) ) { result += pix; i++; }
if (!isnan(pix = pixel(p2+1, q2 )) ) { result += pix; i++; }
if (!isnan(pix = pixel(p2 , q2+1)) ) { result += pix; i++; }
if (!isnan(pix = pixel(p2+1, q2+1)) ) { result += pix; i++; }
return i > 0 ? result / i : NAN;
} else { // not need interpolation for q
if (!isnan(pix = pixel(p2 , q2 )) ) { result += pix; i++; }
if (!isnan(pix = pixel(p2+1, q2 )) ) { result += pix; i++; }
return i > 0 ? result / i : NAN;
}
} else { // not need interpolation for p
if(q % 2){ // need interpolation for q
if (!isnan(pix = pixel(p2 , q2 )) ) { result += pix; i++; }
if (!isnan(pix = pixel(p2 , q2+1)) ) { result += pix; i++; }
return i > 0 ? result / i : NAN;
} else { // not need interpolation for q
return pixel(p2, q2);
}
}
}
void PDESolver2D::dump(const char *file_name)
{
FILE *f = fopen(file_name, "w");
fwrite(pixels, sizeof(double), n*n, f);
fclose(f);
}
利用コード †
main.cpp †
LANG:cpp
#include "pdesolver2d.h"
class SheetConductorSolver : public PDESolver2D
{
public:
SheetConductorSolver(int n)
: PDESolver2D(n)
{ }
PDESolver2D *create_instance(int n)
{ return new SheetConductorSolver(n); }
double calc_new_value(double c, double t, double r, double b, double l, int p, int q);
};
double SheetConductorSolver::calc_new_value(double c, double t, double r, double b, double l, int p, int q)
{
return 0.25 * (t + r + b + l); // Laplace
}
////////////////////////////////////////////////////////
double sqr(double v) { return v*v; }
void set_boundary(PDESolver2D *solver)
{
for(int p = 0; p < solver->size(); p++){
for(int q = 0; q < solver->size(); q++){
// outer boundary
if( p==0 || q==0 || p==solver->size()-1 || q==solver->size()-1 )
solver->pixel(p, q, NAN); // free edge
// current injection
double x = 2.0 * p / ( solver->size() - 1 ) - 1.0;
double y = 2.0 * q / ( solver->size() - 1 ) - 1.0;
// circular electrodes
if ( sqr(x+0.5) + sqr(y) < sqr(0.05) ) {
solver->mask(p, q, 1); // fixed edge
solver->pixel(p, q, -1.0);
}
if ( sqr(x-0.5) + sqr(y) < sqr(0.05) ) {
solver->mask(p, q, 1); // fixed edge
solver->pixel(p, q, +1.0);
}
}
}
}
PDESolver2D *solver = NULL;
// ^C が押されたら現在の計算を中断する
void signal_received(int sig)
{
if(solver)
solver->interrupt();
}
int main(int argc, const char *argv[])
{
int initial_size = 17;
solver = new SheetConductorSolver(initial_size);
// ^C が押されたら signal_received へ飛ぶ
signal(SIGINT, signal_received);
// 徐々に解像度を上げながら計算する
char fname[256];
double delta = 1e-6;
FILE *log;
// 0 1 2 3 4 5 6
// 17, 33, 65, 129, 257, 513, 1025
for(int i = 0; i < 7; i++) {
solver->set_speed(1);
set_boundary(solver);
sprintf(fname, "solver%dbefore.data", i);
solver->dump(fname);
sprintf(fname, "solver%d.log", i);
log = fopen(fname, "w");
int success = solver->solve(delta, log);
fclose(log);
if(success){
sprintf(fname, "solver%dafter.data", i);
} else {
sprintf(fname, "solver%dinterrupted.data", i);
}
solver->dump(fname);
fprintf(stderr, "\n*********** writing %s \n", fname);
int delete_original = 1;
solver = solver->create_double(delete_original);
}
}
コンパイル&実行 †
LANG:console $ ls main.cpp pdesolver2d.cpp pdesolver2d.h $ g++ -O4 main.cpp pdesolver2d.cpp $ ls *a.out main.cpp pdesolver2d.cpp pdesolver2d.h $ ./a.out step ( 337, 9.730739e-07, 0.0s) *********** writing solver0after.data step ( 948, 9.985805e-07, 0.0s) *********** writing solver1after.data step ( 3011, 9.996066e-07, 1.0s) *********** writing solver2after.data step ( 5274, 9.995926e-07, 1.0s) *********** writing solver3after.data step ( 464, 9.984991e-07, 1.0s) *********** writing solver4after.data step ( 958, 9.997507e-07, 5.0s) *********** writing solver5after.data step ( 1402, 9.997880e-07, 29.0s) *********** writing solver6after.data $
この系は素性がいいので、speed = 1.5 にするとさらに 1.5 倍速くなるけれど、 speed = 2 では発散する。
計算結果ファイル †
solver?after.data
のような名前のファイルが格段の計算結果となる。
LANG:cpp double pixels[n*n];
の内容を単にダンプしたものなので、sqrt( (ファイルサイズ)/8バイト ) で n を求めて、 n*n の二次元配列として double 値を読み込み、グラフソフトで表示することになる。
Igor Pro なら、
LANG:igor
function show(filename)
string filename;
GBLoadWave/B/T={4,4}/W=1/O filename
variable n = sqrt(numpnts(wave0))
make/O/N=(n,n) image
wave wave0, image
image = wave0[p+q*n]
setscale x,0,2,image
setscale y,-1,1,image
end
を使って、
LANG:command
*show("z:/electric-field2/solver6after.data")
*newimage image
*ModifyImage image ctab= {*,*,Rainbow,0}
とすればカラー表示できる。
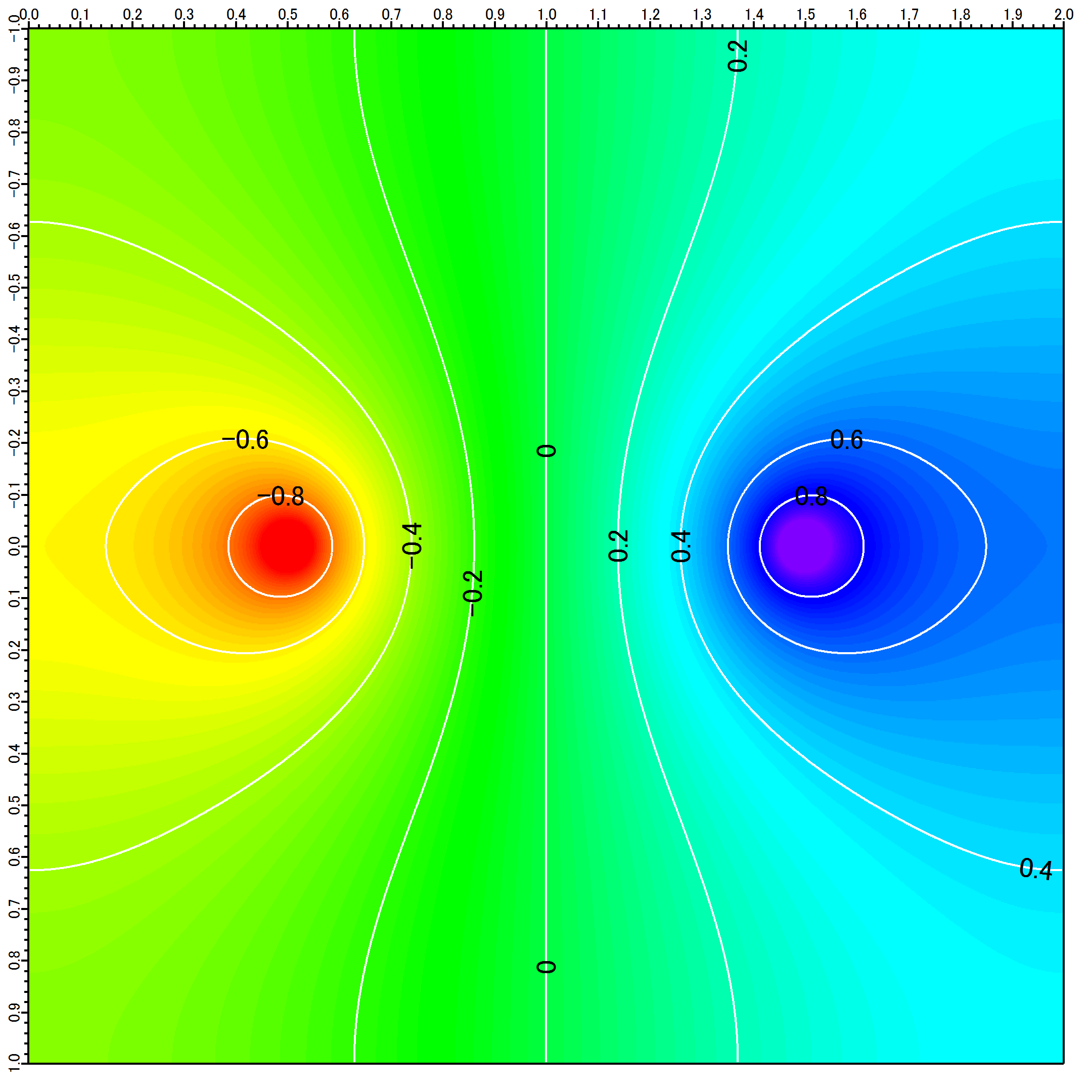
等高線 †
[グラフ]-[グラフに追加]-[等高線プロット]
から、
[アピアランス] の
- [ラインカラー] を [すべて同じカラー]-[白]
- [ラベル詳細] で、
- [背景] を [透明]
- [ラベルテキスト]-[カラー]-[黒]
とすれば、
LANG:console *AppendMatrixContour/T image *ModifyContour image rgbLines=(65535,65535,65535),labelBkg=1,labelRGB=(0,0,0)
と同等の動作になり、
が得られる。
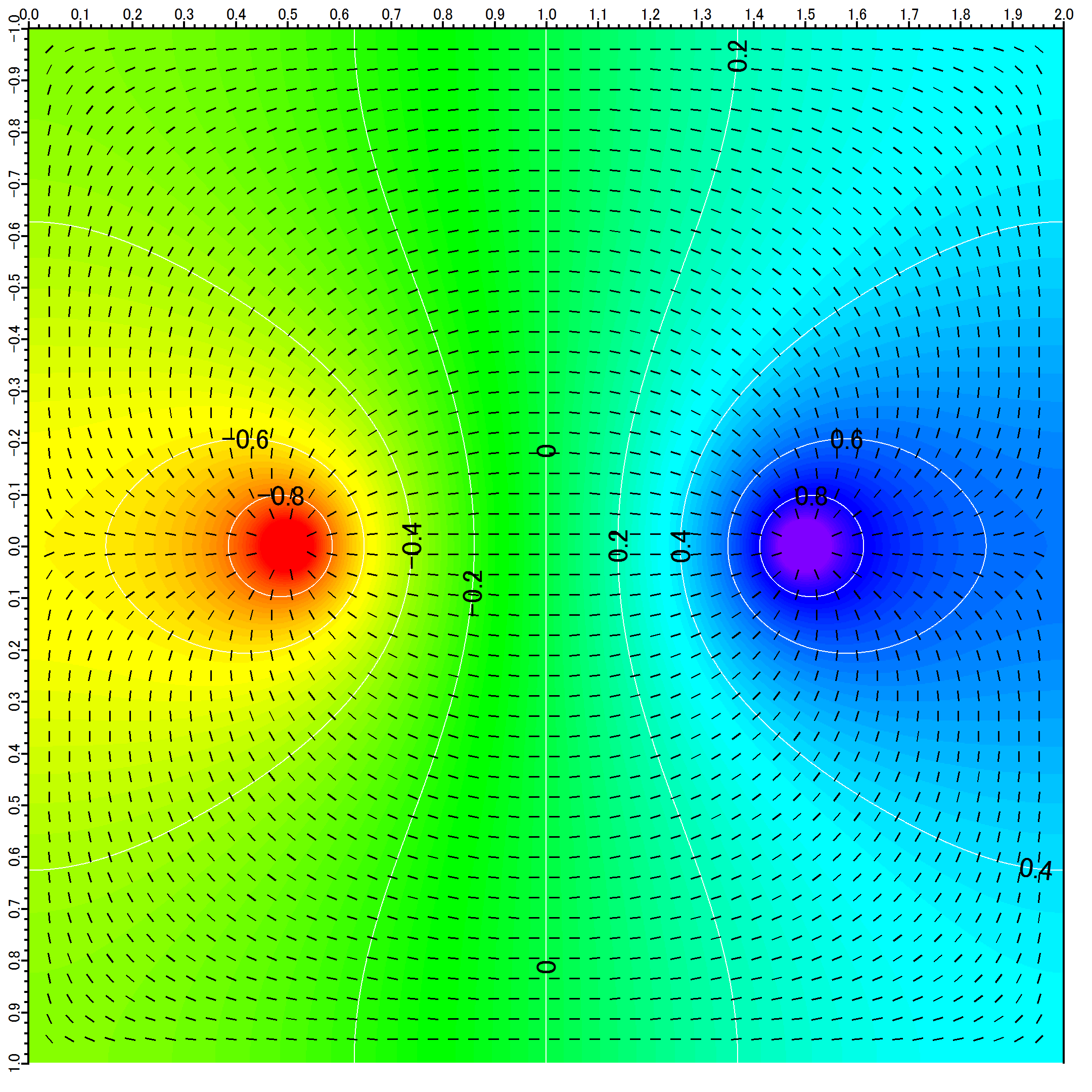
電場強度を見るには †
強度のみであれば をプロットすればいい。
Igor Pro なら、
LANG:console *duplicate image, image2 *image2 = sqrt((p == 0 ? image[p+1][q]-image[p][q] : image[p][q]-image[p-1][q])^2+(q == 0 ? image[p][q+1]-image[p][q] : image[p][q]-image[p][q-1])^2) *image2 = image2 == 0 ? NaN : image2
電場の方向を見るには †
function calcfield()
wave image
variable n = dimsize(image,0)
variable d = 20
variable pp, qq, nn = trunc((n-1)/d)
variable ma = 0
make/O/N=(nn*nn) posx, posy
make/O/N=(nn*nn,2) field
for(pp=0; pp<nn-1; pp+=1)
for(qq=0; qq<nn-1; qq+=1)
posx[pp+qq*nn] = DimOffset(image, 0) + DimDelta(image, 0) * pp * d
posy[pp+qq*nn] = DimOffset(image, 1) + DimDelta(image, 1) * qq * d
variable fieldx = -image[pp*d+1][qq*d ]+image[pp*d][qq*d]
variable fieldy = image[pp*d ][qq*d+1]-image[pp*d][qq*d]
variable fieldr = sqrt(fieldx^2+fieldy^2)
if (fieldr > ma)
ma = fieldr
endif
field[pp+qq*nn][1] = atan2(fieldy, fieldx)
endfor
endfor
field[][0] = 40 // 長さ
end
として、
LANG:console
*calcfield()
*appendtograph/t/l posy vs posx
*ModifyGraph mode=3,arrowMarker(posy)={field,0.5,0,0.5,1},msize=0.1
*ModifyGraph rgb(posy)=(0,0,0)
などとすれば、下記のようなグラフを得る。
円柱座標の場合の計算 †
誘電率が均一な場合、上記のラプラシアンを変形して、
そのまま差分方程式に直すと、
整理すると、
calc_new_value 中でこの式を使えば正しい計算結果が得られる。
すなわち、
LANG:cpp
class CylindricalSolver : public PDESolver2D
{
public:
CylindricalSolver(int n)
: PDESolver2D(n)
{ }
PDESolver2D *create_instance(int n)
{ return new CylindricalSolver(n); }
double calc_new_value(double c, double t, double r, double b, double l, int p, int q);
};
double CylindricalSolver::calc_new_value(double c, double t, double r, double b, double l, int p, int q)
{
return 0.25 * (t + r + b + l) + 0.125 * (r - l) / p; // Cylindrical Laplace
}
とすればソルバーの完成。
あとは、
LANG:cpp
void set_boundary(PDESolver2D *solver, double r1, double r2, double d)
{
for(int p = 0; p < solver->size(); p++){
for(int q = 0; q < solver->size(); q++){
// outer boundary
if( p==0 || q==0 || p==solver->size()-1 || q==solver->size()-1 )
solver->pixel(p, q, NAN); // free edge
// coordinate
double r = 2.0 * p / ( solver->size() - 1 );
double z = 2.0 * q / ( solver->size() - 1 ) - 1.0;
if(d/2<z && z<d/2+0.1 && r<r1) {
solver->pixel(p, q, 0); // ground
}
if(-d/2<z && z<-d/2-0.1 && r<r2) {
solver->pixel(p, q, 1); // biased
}
}
}
}
のようにして境界条件を与えればいい。
誘電率が不連続に変化する場合 - 有限要素法を使う †
上記のように誘電率や伝導度が均一の時は差分方程式をそのままヤコビ法で解いてうまく行くのに対して、 誘電率が不連続に変化する系に対して無理やり差分方程式を立てて解こうとしても、 繰り返し計算が発散してしまいうまく計算できない。
参考:
http://www.yamamo10.jp/yamamoto/study/electromagnetics/change_electric_constant/laplace.pdf
差分法はこのように誘電率が異なる静電場の計算には適さない
そこでどうするかというと、有限要素法により漸化式を得るのが良いそうだ。
平面での漸化式 †
停留条件は、
これを整理した漸化式は、
となる。
これも上下左右の格子点の値しか使っていないため、加えて epsilon(x,y) を与えてやることで 上記のソルバーを使って解ける。
円柱座標での漸化式 †
円柱座標の場合、対応する停留条件は、
整理すると、
となる。
コメント・質問 †
自由端の境界条件についての質問 †
くろぐろ? ()
メモを拝見させていただきました. 等電位線のシミュレーションを行おうとしていたのでとても役立ちました. 表題の件について質問です.
自由端において, 領域外の値としてφpqを使用することで∂φ/∂x=0が満たされるといのことですが, この条件は領域端を走る電気力線に対して等電位線が垂直に交わることを表しているのでしょうか? また, φpqを使用すると, なぜこの条件が満たされるのでしょうか?
この質問に答えていただけると幸いです.
添付ファイル: