不純物散乱の効果を正しく取り込む : vertex 補正の必要性 †
(9.28)
この補正が出てくる理由が分からない。
(8.118) および (9.4J) を完全に評価する限り
近似は入っていないと思っていたのだけれど・・・
ここまで、近似というか、多少なりともごまかしが入ったのは
- (8.101), (8.101') で初期条件がおかしくなったこと
- (8.119) の不純物平均
- (8.123) の実部は無視できるのか
くらい?
- (9.28) の項は (9.4) 式の高次項ではない
- (9.5) 式の
を
で展開した形に似ている
- それならなぜ (9.28) 式の
は
でないのか?
- この項は (8.118) や (9.4J) の導出中に行われた近似で落とされていたのに
気付かなかった?
あたりが疑問。
(9.4) 式の高次項ではない †
(9.4) 式は
で展開しているので、高次項には
の2次以上が含まれるはずだが、
(9.28) に
は1つしか入っていない。
(9.5) 式の g を g0 で展開した形に似ている †
(8.121) より、
この1項目と2項目とを掛け合わせると、
の項が出る。
にこれらをそのまま入れると、かなり似た項は出るが、(9.28) そのものは出ない。
そもそも、こういう項は
や
の形になるから、どうも話が違う。
これらの過程は (9.27) の
に含まれている、上下どちらかに1つ耳の生えたタイプということで、
改めて組み込む必要は無いということだと思う。
なぜ (9.28) 式の
は
でないのか †
上下に耳が生える過程を組み込むため?
これまでの近似で落とされていたのに気付かなかった? †
たぶんそう。
どこから出てくるのだろう?
・・・不純物平均のところしかなさそうだ。
上で見たとおり、(9.28) の項は
の2次の項とゼロ次の項を掛けた物ではなく、
1次の項を2つ掛けた物になっている。
8-10 では1次の項は不純物平均により消えるとされたけど、
ポテンシャルがあると残る物が出てくるのかも。
不純物平均の前に戻ってみる †
と考えるのをやめて、
として、8-10、8-11 を見直してみる。
が入っているため不純物平均を取る直前の式に戻ろう。
と置けば、
(8.117) は
(8.145) は
となる。
ポテンシャルを3回含む項を評価する †
この2つの式を使ってポテンシャルを3回含む項を取り出してみる。
→ (9.28) が
と
の3つのポテンシャル成分を含んでいることに注意。
それ以外の項は下線を引いて、どんどん消していく。
同様にして、
したがって、
0次:
1次:
2次:
3次:
これらの展開式は
でいうところの (8.118) の各項に相当するもので、
内部から
を除き、
のみの式とした成分を略して、
の1次であれば
、
2次であれば
、3次であれば
のように
教科書では表されている。
これが (9.5), (9.28) などの表記である。
目的の項はどれか? †
3次の項は、
の形になる。
3回出てくる
を展開する際、
と
のどちらを取るかで様々な項が出るが、
複数の
を含む場合、それらの
は互いに打ち消し合うように
取らないと不純物平均によりゼロになる。
そのように考えると、
と
が両方出てくる項は3次が最低次になる。
すなわち、2つの
が打ち消し合い、さらに
を1つ含む形である。
から
を2つ、
を1つ取るような積を作ると、
の3つが考えられる。
このうち1番目と3番目は上の
(9.5) 式の g を g0 で展開した形に似ている
で見たように (9.26) に含まれている。
実際、(9.26) には
をまたがずに完結する
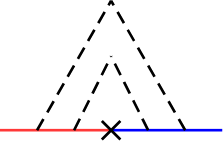
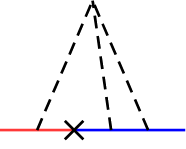
の寄与は全て取り入れられている。(図の「耳」に相当する)
すなわち取り入れ忘れているのは2番目の形で、
をまたぐような
の項である。
はその最も単純な項である。

である。
不純物平均を入れる †
不純物平均により
が要求されるため、
下線部は打ち消し合うため、
この式の変数を適当に書き換えると (9.29) の
を
に書き換えた式が出てくる。
g0 を g に書き換える †
その
を
に書き換えると (9.29) になる。
を
に変えるのは、
の部分が
と
の積になるような高次項を取り入れるためである。
→ (9.5) 式の g を g0 で展開した形に似ている
で見た内容が参考になる。
すなわち、
という部分を、
と書き換えることにより、(8.118) のように
であることから、
のような高次項をすべて考慮に入れられる、ということである。
ただし、教科書の式では上記の
の因子が抜けている。
ファインマン図の意味 †
上と下は
と相互作用する前後の、ωの異なる部分で、
その間に打ち消し合う2つの q があることを表す図になっている
わけですね。
輪になっている部分を開くと、

となる。
×のところが
で、そこで
が変化する。
その前後の
が互いに打ち消し合う。
思うこと †
なんか・・・始めから上記の手順 (
とする)
でやってくれた方が分かりやすいと思うのだけれど、
どうして教科書はああいう書き方になっているのだろう???
→ (9.60) の後に解説があって、
摂動計算に於いて展開パラメータを明らかにしておく上で便利なため、
他の多くの文献でも不純物散乱の寿命を取り込んだ Green 関数を基本に考え、
必要に応じて vertex 補正を行うのだそうだ。
上のように1から展開した方が「すっきりする」とも書いてあった。
補正項を評価する †
ようやく教科書を読み進められる(汗
(9.29)
和の部分を略記すると、
括弧内は
の項が支配的で、
や
の項は小さいと書かれているが、
まだ納得はいっていない。
恐らく (9.8-1) と (9.8-2) との比較と同様の話になるのだと思うけれど、後で見直す。
支配的と言われる項は、
(9.30)
となって、これは (9.8) に
の掛かった項となる。
したがって、
(9.32)
(9.40) の評価 †
第1式は通常通りで、
(複号は上が
下が
) なので、
(9.40-1)
第2式は
が入っているのでちょっと大変。
より、
を用いた。
ここで、
したがって、
(9.40-2)
教科書に出てくる
という項は、
(9.42)
を入れると、
となって、上記の値と一致する。
教科書は (9.39) と (9.40-2) とで
倍の因子を2回間違って、結果的には合っているみたい。
(9.41)
(9.43) は (9.30) と見比べると
が2乗で掛かっていたのを見落としている気がするんだけれど、
どうなんだろう?
(9.44) も、
-
では
を仮定しておいて高次項ではより正確に組み込んでいる不整合
- たぶん、0 次と 1 次との間に余計な項が出現している
という点でおかしい。(結果的には微少量しか異ならないけど)
以下でちゃんとやってみたい。