射影・直和・直交直和
目次 †
ベクトルの成分 †
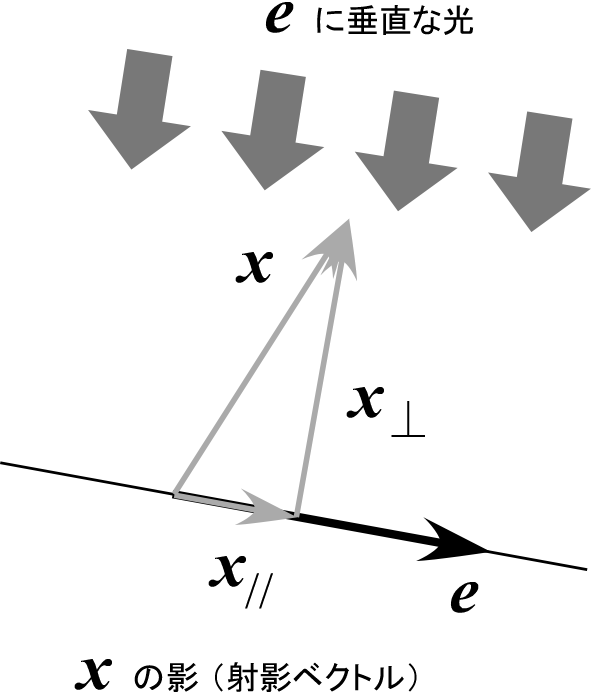
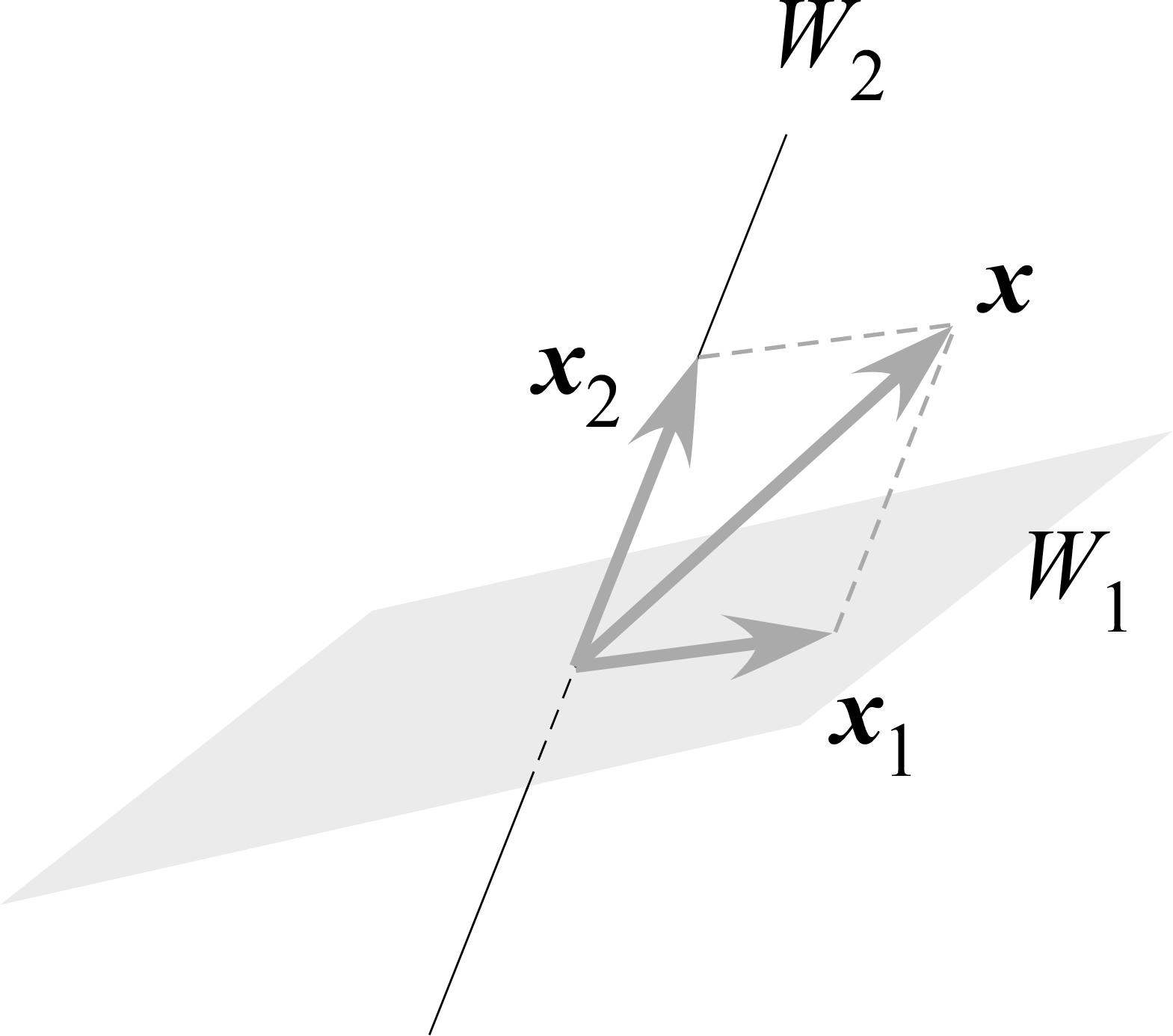
規格化されたベクトル $\bm e$ に対して、ベクトル $\bm x$ を
- $\bm e$ に平行な成分 $\bm x_{\parallel}=x_\parallel \bm e$ と、
- $\bm e$ に垂直な成分 $\bm x_{\perp}$ とに分解して、
$\bm x=\bm x_{\parallel}+\bm x_{\perp}$ と表すことを考えよう。
両辺に左から $\bm e$ をかければ、
$$\begin{aligned}(\bm e,\bm x)=x_{\parallel}(\bm e,\bm e)+(\bm e,\bm x_{\perp})=x_{\parallel}\end{aligned}$$
が得られ、
$$\bm x_{\parallel}=\underbrace{(\bm e,\bm x)}_{\text{大きさ}}\,\underbrace{\bm e\rule[-3pt]{0pt}{0pt}}_\text{向き}$$ $$\begin{aligned}\bm x_{\perp}=\bm x-\bm x_\parallel=\bm x-(\bm e,\bm x)\bm e\end{aligned}$$
としてこれらのベクトルを求められる。
(同じことをグラム・シュミットの直交化で行った)
この $\bm x_\parallel$ を $\bm x$ の $\bm e$ への正射影と呼ぶ(直交射影あるいは単に射影とも)。
$\bm e$ に垂直な光を $\bm x$ に当てたとき、 $\bm e$ 軸上にできる影が $\bm x_\parallel$ であるという気持ちが込められている → 「射影」
注意1 †
例えば $xy$ 平面上のベクトル $\bm v=\begin{pmatrix}2\\3\end{pmatrix}$ に対して、「$\bm v$ の $x$ 方向成分 は $2$ である」と言う場合と 「$\bm v$ の $x$ 方向成分 は $\begin{pmatrix}2\\0\end{pmatrix}$ である」と言う場合と があるので、 どちらを指しているのかは文脈から読み取るように。
注意2 †
規格化されていない $\bm v$ 方向の成分を求めるなら、$\bm e=\bm v/\|\bm v\|$ だから、
$$\begin{aligned}\bm x_{\parallel}=(\frac{\bm v}{\|\bm v\|},\bm x)\,\frac{\bm v}{\|\bm v\|}=\frac{(\bm v,\bm x)}{\|\bm v\|^2}\bm v\end{aligned}$$
注意3 †
複素ベクトルに対しては $(\bm x,\bm e)\ne(\bm e,\bm x)$ なので、 どちらから掛けるかが重要である。
$(\bm e,\bm x)=(\bm e,x_\parallel \bm e)=x_{\parallel}$ だが、
$(\bm x,\bm e)=(x_\parallel \bm e,\bm e)=\overline{x_{\parallel}}$ となってしまう。
注意4 †
この授業では $(\bm a,k\bm b)=k(\bm a,\bm b)$ となる内積の公理を採用しているため 上記が正しいが、
$(k\bm a,\bm b)=k(\bm a,\bm b)$ を採用する場合には左ではなく右から掛ける必要がある。
この説明でピンとこない学生は 計量空間に関する説明 を見直すこと。
射影演算子 †
$\bm x$ から $\bm e$ に平行な成分 $\bm x_\parallel$ を求める演算、
$$P_{\bm e}:\bm x\mapsto\bm x_\parallel\text{ あるいは同じことだが }P_{\bm e}:\bm x\mapsto(\bm e,\bm x)\bm e$$
は線形変換であり、$P_{\bm e}$ は射影変換あるいは射影演算子と呼ばれる。
ある正規直交基底 $A$ の下で射影変換の行列表現を求めよう。数ベクトル $\bm a_A,\bm b_A$ の標準内積に対して、
$$\begin{aligned} (\bm a_A,\bm b_A)&=\sum_k^n \overline{a_k}b_k=\begin{pmatrix}\overline a_1&\overline a_2&\dots&\overline a_n\end{pmatrix} \begin{pmatrix}b_1\\b_2\\\vdots\\b_n\end{pmatrix}={}^t\overline {\bm a_A}\bm b_A=\bm a_A^\dagger\bm b_A \end{aligned}$$
となることを用いて、
$$\begin{aligned} (\bm x_{\parallel})_A &=(\bm e_A,\bm x_A)\bm e_A\\ &=\{\bm e_A^\dagger \bm x_A\}\bm e_A\\ &=\bm e_A\{\bm e_A^\dagger \bm x_A\}\hspace{1cm}\because \{\ \}\,\text{部は}1\times 1\text{行列}\\ &=\{\bm e_A\bm e_A^\dagger\}\bm x_A\hspace{1cm}\because \text{結合法則}\\ &=(P_{\bm e})_A\,\bm x_A\\ \end{aligned}$$
すなわち $P_{\bm e}$ の表現は、任意の正規直交基底 $A$ に対して次のように表せる。
$$\begin{aligned} (P_{\bm e})_A&=\bm e_A\bm e^\dagger_A= \begin{pmatrix} e_1\\e_2\\\vdots\\e_n \end{pmatrix} \begin{pmatrix} \overline{ e_1}&\overline{ e_2}&\dots&\overline{ e_n} \end{pmatrix}\\ &=\begin{pmatrix} e_1\overline{e_1}&e_1\overline{e_2}&\cdots&e_1\overline{e_n}\\ e_2\overline{e_1}&e_2\overline{e_2}&&\vdots\\ \vdots&&\ddots&\vdots\\ e_n\overline{e_1}&\cdots&\cdots&e_n\overline{e_n} \end{pmatrix} \end{aligned}$$
例 †
$\bm x=\begin{pmatrix}x\\y\\z\end{pmatrix}$ の $\bm v=\begin{pmatrix}1\\-1\\0\end{pmatrix}$ 方向成分を求めよう。
$\bm e=\frac{1}{\|\bm v\|}\bm v=\frac{1}{\sqrt 2}\begin{pmatrix}1\\-1\\0\end{pmatrix}$ を用いて普通にやれば、
$$ \bm x_\parallel=(\bm e,\bm x)\bm e=\frac{x-y}2\begin{pmatrix}1\\-1\\0\end{pmatrix} $$
同じことを射影演算子を求めて行えば、
$$ P_{\bm v}=P_{\bm e}=\bm e\bm e^\dagger =\frac{1}{2}\begin{pmatrix}1\\-1\\0\end{pmatrix}\begin{pmatrix}1&-1&0\end{pmatrix} =\frac{1}{2}\begin{pmatrix}1&-1&0\\-1&1&0\\0&0&0\end{pmatrix} $$
$$\begin{aligned}\bm x_\parallel&=P_{\bm v}\bm x\\ &=\frac{1}{2}\begin{pmatrix}1&-1&0\\-1&1&0\\0&0&0\end{pmatrix}\begin{pmatrix}x\\y\\z\end{pmatrix} =\frac{1}{2}\begin{pmatrix}x-y\\-x+y\\0\end{pmatrix} =\frac{x-y}{2}\begin{pmatrix}1\\-1\\0\end{pmatrix}\hspace{1cm}\parallel \bm v \end{aligned}$$
$\bm v$ に垂直成分を求めれば、
$$\begin{aligned}\bm x_\perp&=\bm x-\bm x_\parallel\\ &=\begin{pmatrix}x\\y\\z\end{pmatrix}-\frac{x-y}{2}\begin{pmatrix}1\\-1\\0\end{pmatrix} =\begin{pmatrix}(x+y)/2\\(x+y)/2\\z\end{pmatrix} \end{aligned}$$
これは明らかに $\bm v$ と直交する。
当然、
$$ \bm x_\parallel+\bm x_\perp=\begin{pmatrix}x\\y\\z\end{pmatrix}=\bm x $$
が成り立つ。
射影演算子はエルミートになる。 †
$$\begin{aligned} (P_{\bm e})_A^\dagger=\big(\bm e_A\bm e_A^\dagger\big)^\dagger=\big(\bm e_A^\dagger\big)^\dagger\bm e_A^\dagger=\bm e_A\bm e_A^\dagger=(P_{\bm e})_A \end{aligned}$$
より、射影演算子の表現行列はエルミートである。
このとき、任意のベクトル $\bm x,\bm y$ に対して
$$\begin{aligned} (\bm x,P_{\bm e}\bm y)=(P_{\bm e}^\dagger\bm x,\bm y)=(P_{\bm e}\bm x,\bm y) \end{aligned}$$
が成り立ち、このような演算子はエルミート演算子と呼ばれる。
演習問題 †
(1) 三次元複素数ベクトル空間 $C^3$ において、$\bm v=\begin{pmatrix}-1\\2\\i\\\end{pmatrix}$ 方向への射影演算子となる行列 $P_{\bm v}$ を求めよ。また、$\bm x=\begin{pmatrix}1\\0\\1\end{pmatrix}$ の $\bm v$ 方向成分 $\bm x_\parallel$ を求めよ。(余力があれば、内積を使って求めた結果と、$P_{\bm v}$ を使って求めた結果とが一致することを確かめよ)
(2) $x$ の2次以下の複素係数多項式空間 $P^2[x]=\{ax^2+bx+c\,|\,a,b,c\in C\}$ を考える。内積 $(f,g)=\int_{-1}^1 \overline{f(x)}g(x)dx$ に対して $x^2+1$ を $3x-i$ に平行な成分と垂直な成分とに分解せよ。(余力があれば、求めた平行成分と垂直成分とが実際に直交することを確認せよ)
解答例 †
(1) †
三次元複素数ベクトル空間 $C^3$ において、$\bm v=\begin{pmatrix}-1\\2\\i\\\end{pmatrix}$ 方向への射影演算子となる行列 $P_{\bm v}$ を求めよ。また、$\bm x=\begin{pmatrix}1\\0\\1\end{pmatrix}$ の $\bm v$ 方向成分 $\bm x_\parallel$ を求めよ。(余力があれば、内積を使って求めた結果と、$P_{\bm v}$ を使って求めた結果とが一致することを確かめよ)
$\bm v$ を規格化すると $\bm e=\bm v/\|\bm v\|=\bm v/\sqrt{6}$ であるから、
$$ \begin{aligned} P_{\bm v}&=P_{\bm e}=\bm e\bm e^\dagger=\frac16\begin{pmatrix}-1\\2\\i\end{pmatrix}\begin{pmatrix}-1&2&-i\end{pmatrix}\\ &=\frac16\begin{pmatrix} 1&-2&i\\ {}-2&4&-2i\\ {}-i&2i&1 \end{pmatrix} \end{aligned} $$
対角線を挟んで対称な成分が確かに複素共役の関係にあり、エルミートとなっていることを確認できる。($-2\leftrightarrow-2$ や $i\leftrightarrow-i$ や $-2i\leftrightarrow2i$)
$$ \begin{aligned} \bm x_\parallel&=P_{\bm v}\bm x=\frac16\begin{pmatrix} 1&-2&i\\ {}-2&4&-2i\\ {}-i&2i&1 \end{pmatrix}\begin{pmatrix}1\\0\\1\end{pmatrix}\\ &=\frac16\begin{pmatrix}1+i\\-2-2i\\-i+1\end{pmatrix} =\frac{-1-i}6\begin{pmatrix}-1\\2\\i\end{pmatrix} \end{aligned} $$
普通に内積を使って求めるなら、
$$ \begin{aligned} \bm x_\parallel&=(\bm e,\bm x)\bm e=\frac16\big(-1\cdot1+2\cdot0+(-i)\cdot1\big) \begin{pmatrix}-1\\2\\i\\\end{pmatrix}\\ &=\frac{-1-i}6\begin{pmatrix}-1\\2\\i\\\end{pmatrix} \end{aligned} $$
であり、同じ結果が得られる。
さらに検算として $\bm x=\bm x_\parallel+\bm x_\perp$ の分解を試みると、
$$ \begin{aligned} \bm x_\perp=\bm x-\bm x_\parallel=\begin{pmatrix}1\\0\\1\end{pmatrix}-\frac16\begin{pmatrix}1+i\\-2-2i\\-i+1\end{pmatrix}= \frac16\begin{pmatrix}5-i\\2+2i\\5+i\end{pmatrix} \end{aligned} $$
$$ (\bm v,\bm x_\perp)=\frac16\big(-5+i+4+4i-5i+1\big)=0 $$
として、正しく直交分解できていることを確かめられる。
内積の時に複素共役を取ることを忘れがちなので注意すること。
(2) †
(2) $x$ の2次以下の複素係数多項式空間 $P^2[x]=\{ax^2+bx+c\,|\,a,b,c\in C\}$ を考える。内積 $(f,g)=\int_{-1}^1 \overline{f(x)}g(x)dx$ に対して $x^2+1$ を $3x-i$ に平行な成分と垂直な成分とに分解せよ。(余力があれば、求めた平行成分と垂直成分とが実際に直交することを確認せよ)
$3x-i$ のノルムを求める。
$$ \begin{aligned} \|3x-i\|^2&=(3x-i,3x-i)=\int_{-1}^1 \overline{(3x-i)}(3x-i)dx\\ &=\int_{-1}^1 (3x+i)(3x-i)dx=\int_{-1}^1 (9x^2+1)dx\\ &=\Big[3x^3+x\Big]^1_{-1}=8 \end{aligned} $$
より $\|3x-i\|=\sqrt8$
$$ \begin{aligned} (3x-i,x^2+1)&=\int_{-1}^1 \overline{(3x-i)}(x^2+1)dx=\int_{-1}^1 (3x+i)(x^2+1)dx\\ &=\int_{-1}^1 (\cancel{3x^3}+ix^2+\cancel{3x}+i)dx=\Big[\frac i3x^3+ix\Big]^1_{-1}=\frac{8i}3 \end{aligned} $$
であるから平行成分は
$$ \frac18(3x-i,x^2+1)\cdot(3x-i)=ix+\frac13 $$
垂直成分は
$$ x^2+1-\Big(ix+\frac13\Big)=x^2-ix+\frac23 $$
両者の内積を取れば、
$$ \begin{aligned} &\Big(ix+\frac13,\ x^2-ix+\frac23\Big)=\int_{-1}^1 \overline{\Big(ix+\frac13\Big)}\Big(x^2-ix+\frac23\Big)dx\\ &=\int_{-1}^1 \Big(-ix+\frac13\Big)\Big(x^2-ix+\frac23\Big)dx=\int_{-1}^1 \Big(-\cancel{ix^3}-\frac23x^2-\cancel{ix}+\frac29\Big)dx\\ &=\Big[-\frac29x^3+\frac29x\Big]^1_{-1}=0 \end{aligned} $$
となり、確かに直交していることを確認できる。
$n$ 次元空間への射影を考える †
ここまで、あるベクトルに平行な直線(一次元空間)への射影を考えたが、 以下では平面への射影や、もっと一般に $n$ 次元空間への射影を考える。
そのためにいくつか準備を行う。
復習1:線形空間 †
$K$ 上の線形空間とは、ベクトルの和とスカラー倍について閉じた集合のことだった。
- 任意の $\bm x,\bm y\in V$ に対して、必ず $\bm x+\bm y\in V$
↔ $\bm x,\bm y\in V$ から $\bm x+\bm y\in V$ を導けるということ - 任意の $\bm x\in V,k\in K$ に対して、必ず $k\bm x\in V$
↔ $\bm x\in V,k\in K$ から $k\bm x\in V$ を導けるということ
復習2:部分空間 †
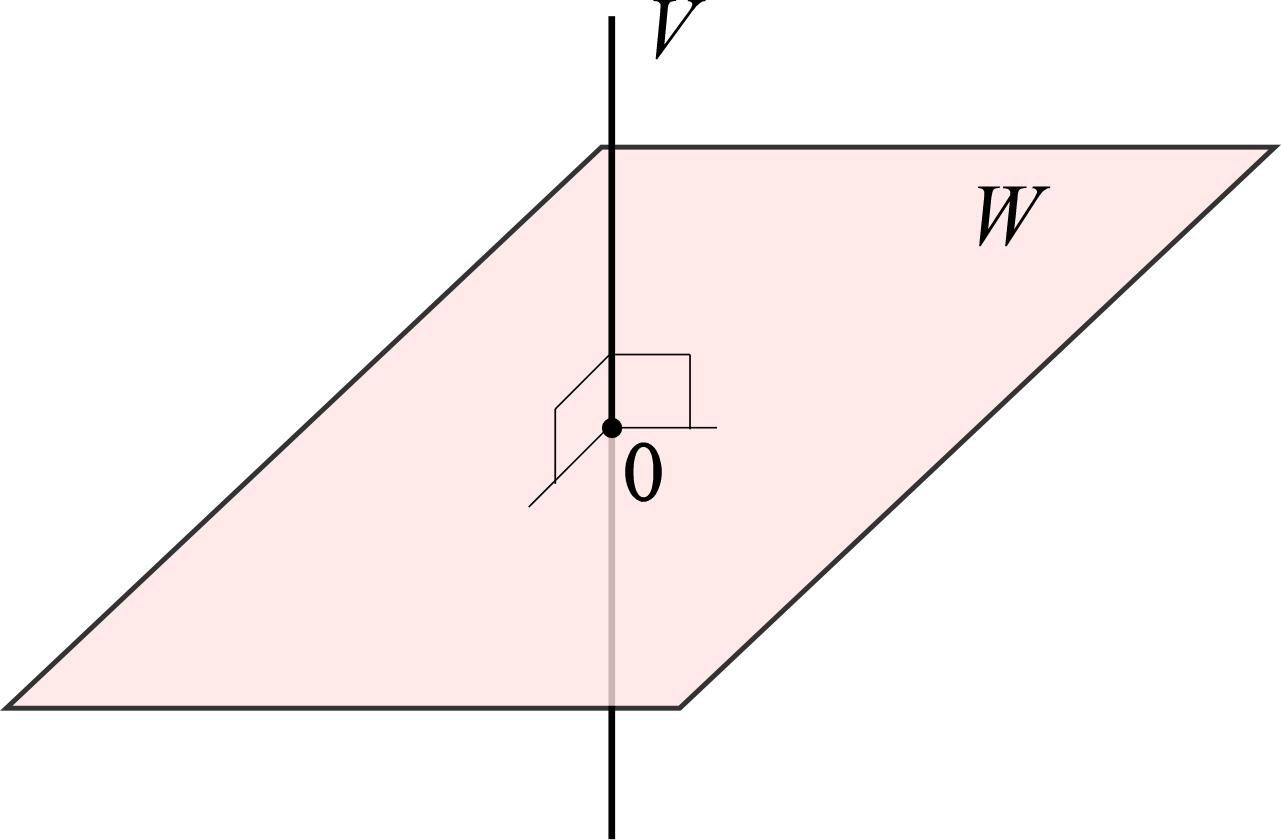
線形空間の部分集合 $W\subset V$ がベクトルの和とスカラー倍について閉じている場合、 $W$ も線形空間となり、$W$ は $V$ の部分空間であるという。
$\mathbb R^3$ の部分空間:全体空間が3次元なので部分空間は3次元以下になる
- 0次元の部分空間は原点のみからなる集合 $\{\,\bm 0\,\}$
- 1次元の部分空間は原点を通る直線 $\{\,\bm p=s\bm a\,|\,s\in K\,\}$
- 2次元の部分空間は原点を通る平面 $\{\,\bm p=s\bm a+t\bm b\,|\,s,t\in K\,\}$
- 3次元の部分空間は $\mathbb R^3$ そのもの
同じ直線的でも、原点を通らない $\{\,\bm p=s\bm a+\bm b\,|\,s\in K\,\}$ は線形空間にならない。(和やスカラー倍が元の集合からはみ出す)
上の例のように $n$ 個のベクトルの線形結合として表せるベクトルの集合を、それらのベクトルが「張る空間」と呼ぶのであった。$n$ 個のベクトルが張る空間の次元は、それらが一次独立であれば $n$ であるが、一次従属であれば $n$ より小さくなる。
復習3:集合の積と和 †
集合 $A$ と集合 $B$ の積と和は、
|
記号の覚え方:
- 「$x\in A\,\text{かつ}\,x\in B$」は英語では「$x\in A\,\text{and}\,x\in B$」
- And の A と $\cap$ とは似ている(でしょ?)
以下、$U$ の部分空間 $V,W$ について考える †
$K$ 上の線形空間 $U$ の部分空間 $V,W$ を考え、
$\{\bm v_1,\bm v_2,\dots,\bm v_n\},$ $\{\bm w_1,\bm w_2,\dots,\bm w_m\}$ をそれぞれの基底とする。
($\dim V=n,\ \dim W=m$)
交空間 $V\cap W$ †
2つの線形空間の、集合としての交わり $V\cap W$ は常に線形空間になり、交空間と呼ばれる。
証明:
$\bm x,\bm y\in V\cap W,\ k\in K$ とする。
$\bm x,\bm y\in V$ かつ $\bm x,\bm y\in W$ であるから、
$\bm x+\bm y\in V$ かつ $\bm x+\bm y\in W$ そして $k\bm x\in V$ かつ $k\bm x\in W$
すなわち、$\bm x+\bm y, k\bm x\in V\cap W$ であり、
$V\cap W$ はベクトルの和とスカラー倍に対して閉じている。
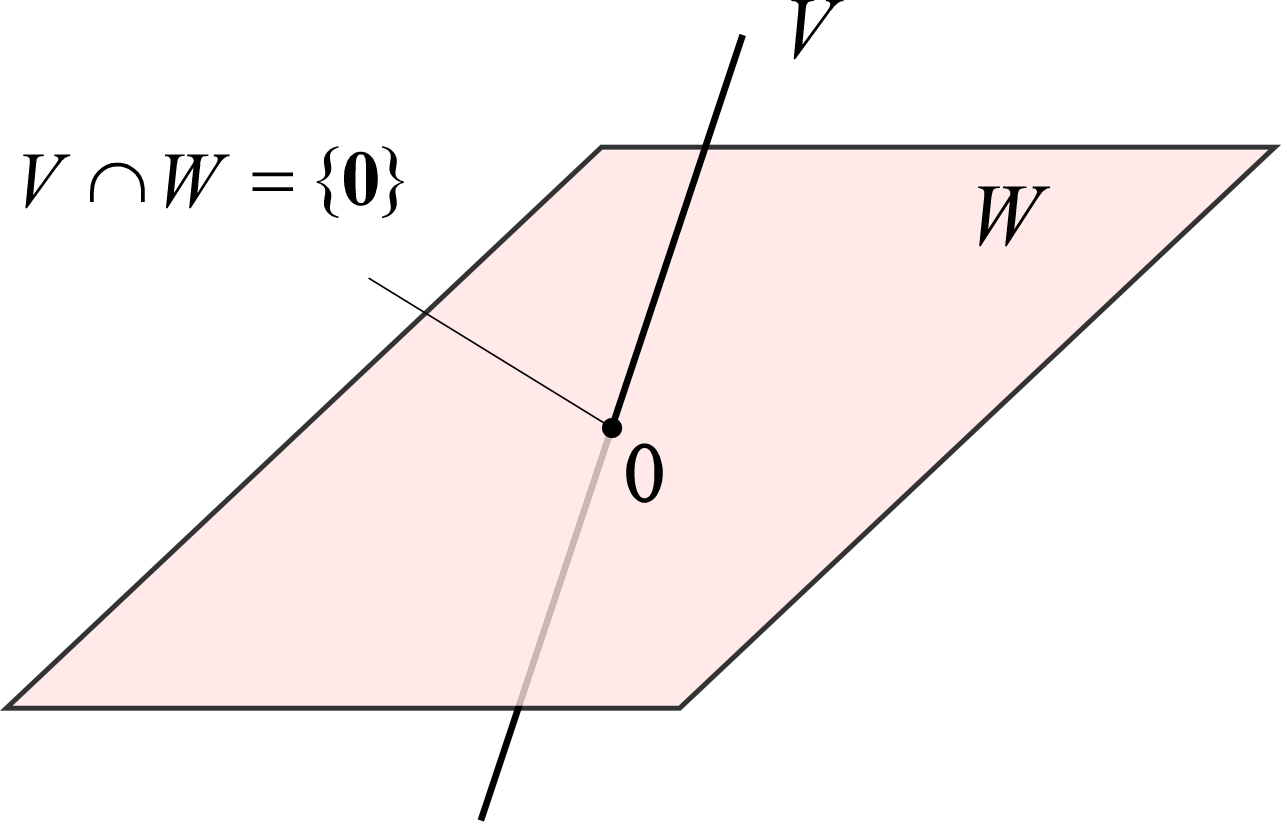
交わり $V\cap W$ が空集合になることはない。
線形空間は必ず $\bm 0$ を含むから、常に $\bm 0\in V\cap W$ である。
$V\cap W=\{\,\bm 0\,\}$ のとき、$\dim(V\cap W)=0$
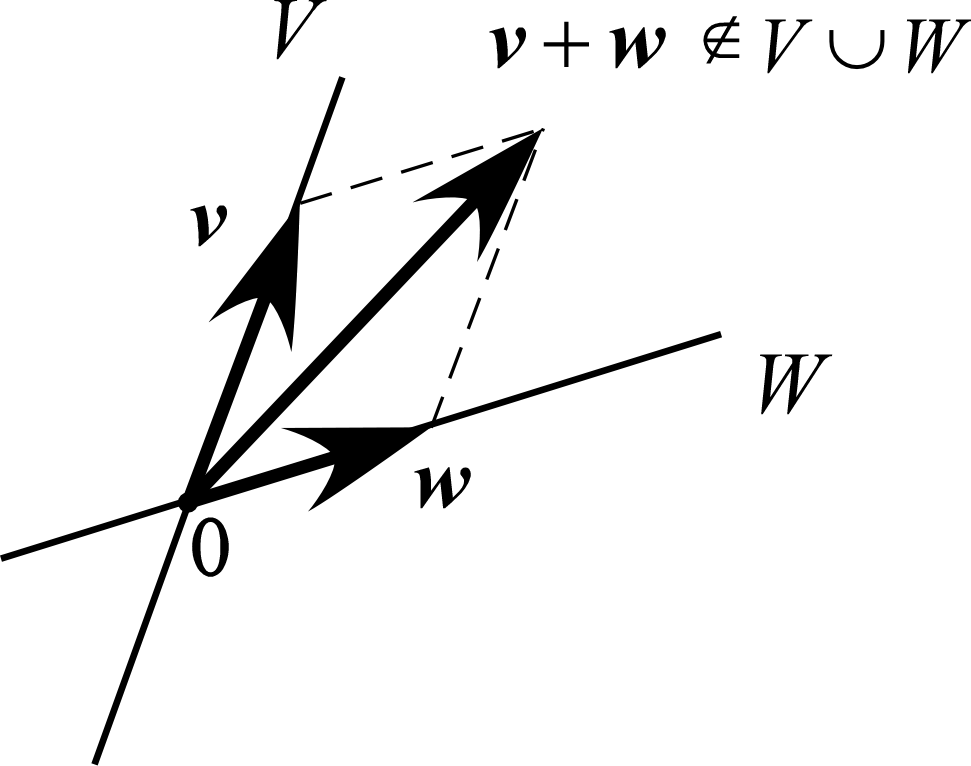
和集合 $V\cup W$ はベクトル和に対して閉じていないことがある †
例えば図のように、2つの1次元空間 $V,W$ の和集合 $V\cup W$ は、 原点で交わる2本の直線の形をしている。
$V,W$ 上から2つのベクトルを取り
$\bm v\in V, \bm w\in W$ とすれば、
$\bm v, \bm w\in V\cap W$ でない限り、
$\bm v+\bm w\notin V\cup W$ である。
すなわち、和集合は必ずしも線形空間にならない
和空間 $V+W$ †
和集合をベクトル和について閉じるように拡大した線形空間が和空間 $V+W$ である。
これは $V$ の元と $W$ の元の和で表せるすべてのベクトルからなる集合である。
$$\begin{aligned}V+W\equiv\{\,\bm x=\bm x_V+\bm x_W\,|\,\bm x_V\in V,\bm x_W\in W\,\}\end{aligned}$$
$\bm x_V\in V,\bm x_W\in W$ はそれぞれ、$V,W$ の基底 $\{\,\bm v_k\,\},\{\,\bm w_k\,\}$ の線形結合として表せるから、 $\bm x\in V+W$ は
$$\begin{aligned} \bm x&=\bm x_V+\bm x_W\\ &=\underbrace{\sum_{k=1}^n c_k\bm v_k}_{\bm x_V}+ {}\underbrace{\sum_{k=1}^m d_k\bm w_k}_{\bm x_W} \end{aligned}$$
のように $V,W$ の基底を合わせた線形結合として表せる。
すなわち、$V,W$ の基底ベクトルすべてで「張られる」空間が和空間である。
ここから $\dim(V+W)\le\dim V+\dim W$ が言える。
$V,W$ の基底ベクトルを合わせたものが一次独立であるときに限り、 それがそのまま $V+W$ の基底となるから、 $\dim(V+W)=\dim V+\dim W$ となる。
和空間の次元 †
一次従属な時は次の式が成り立つ。
$$\begin{aligned}\dim (V+W)=\dim V+\dim W-\dim(V\cap W)\end{aligned}$$
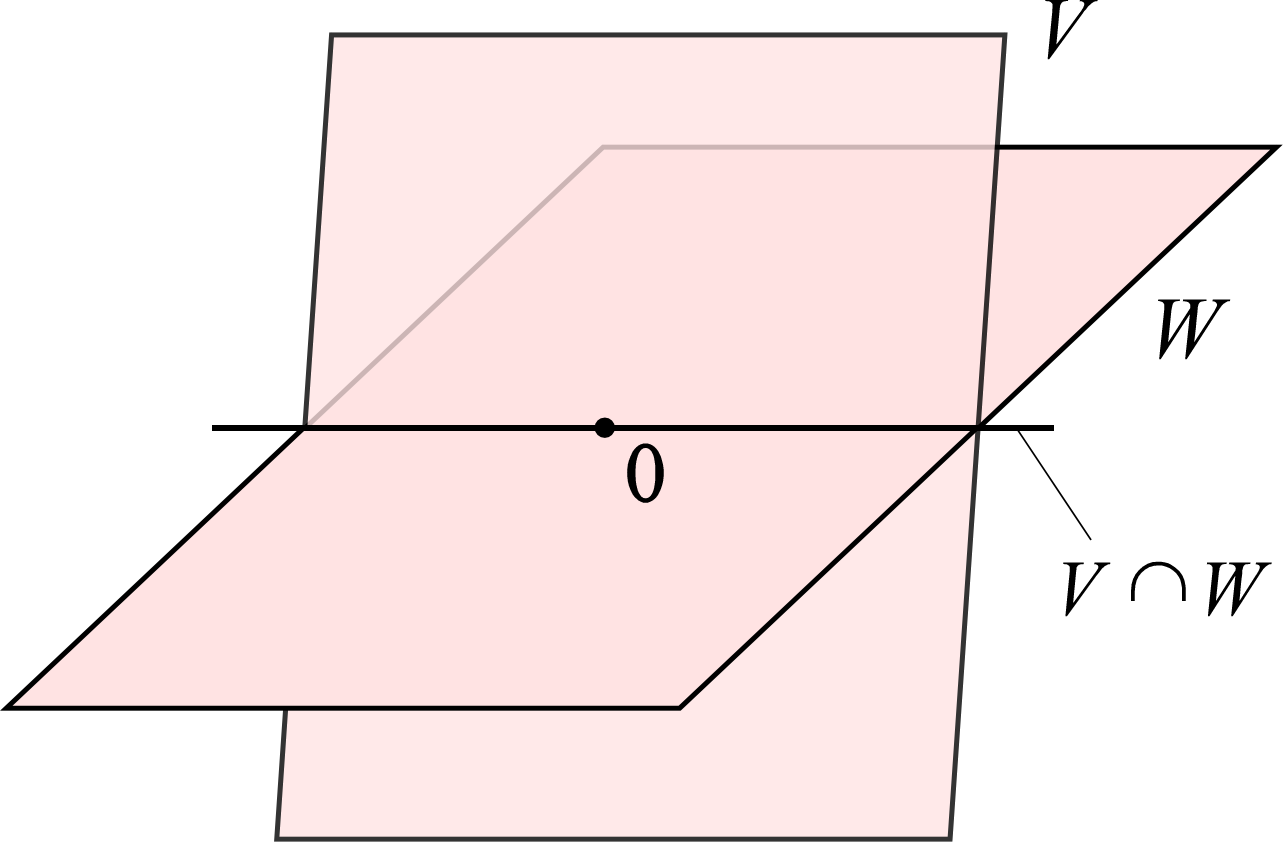
例:
右図の平面状の $V,W$ の和空間は3次元空間全体となる。また2平面の交線が $V\cap W$ に相当する。すなわち、
$$ \underbrace{\dim(V+W)}_3=\underbrace{\dim V}_2+\underbrace{\dim W}_2-\underbrace{\dim(V\cap W)}_1 $$
これは集合 $A\cup B$ の要素の数について ($\#$ は集合の要素の数を表す)
$$ \#(A\cup B)=\#A+\#B-\#(A\cap B) $$
と表せることに対応している。(単に足しておいて重なった部分を引いている)
上の関係式の証明は省くが、次のように考えると理解できるであろう。
- $V\cap W$ の基底 $a$ 個に $\dim(V\cap W)=a$
- $b$ 個のベクトルを加えて $V$ の基底を作成 $\dim V=a+b$
- $c$ 個のベクトルを加えて $W$ の基底を作成 $\dim W=a+c$
- この $b$ 個と $c$ 個とは一次独立になるので (この証明が必要)
- 合わせて $a+b+c$ 個が $V+W$ の基底になる
$$\dim(V+W)=a+b+c=(a+b)+(a+c)-a=\dim V+\dim W-\dim(V\cap W)$$
直和 $V\dot +W$ †
上述の通り、$V,W$ の基底ベクトルを合わせたものが一次独立であるとき、
それらは $V+W$ の基底となって $\dim(V+W)=\dim V+\dim W$ である。
このとき「和空間 $V+W$ は $V$ と $W$ の直和になっている」と言い、
$$\begin{aligned}V+W=V\dot +W\end{aligned}$$
と書く。(プラス記号 $+$ の上に点を書く)
- 直和は「新たな演算」ではない
- 「~~の場合に $V+W$ は直和となる」「~~の場合には直和にならない」といった文脈で用いられる
直和の性質 †
$V\dot +W$ のときには以下が成り立つ:
- $V$ の基底と $W$ の基底は一次独立で、すべて合わせると $V\dot +W$ の基底になる
- $\dim V+\dim W=\dim(V\dot +W)$
- $\bm v\in V$, $\bm w\in W$ が $\bm v+\bm w=\bm 0$ を満たすなら $\bm v=\bm w=\bm 0$ である
$\because$ $\bm v,\bm w$ を基底で分解すれば $\displaystyle\sum_{k=1}^n b_k\bm v_k+\sum_{k=1}^m d_k\bm w_k=\bm 0$
$V$ の基底と $W$ の基底が一次独立なら係数はすべてゼロ - $V\cap W=\{\bm 0\}$
$\displaystyle\because \bm x\in V\cap W \to \bm x=\sum_{k=1}^n b_k\bm v_k=\sum_{k=1}^m d_k\bm w_k$ と表せる
$\displaystyle\sum_{k=1}^n b_k\bm v_k-\sum_{k=1}^m d_k\bm w_k=\bm 0$ となるから係数はすべてゼロ
直和は「互いに線形独立な2つの空間」の和空間のイメージになる。
⇔ $\bm v+\bm w=\bm 0$ から $\bm v=\bm w=\bm 0$ を導ける。
成分分解の一意性 †
$\bm x\in V\dot +W$ のとき $\bm x=\bm x_V+\bm x_W$ $(\bm x_V\in V, \bm x_W\in W)$ の分解は一意に定まる。
証明:
もし二通りに書けたとすると、
$$ \begin{aligned}\bm x&=\bm x_V+\bm x_W\\ &=\bm x'_V+\bm x'_W \end{aligned} $$
両者の差を取って、
$$ \begin{aligned} \bm 0&=\underbrace{(\bm x_V-\bm x'_V)}_{\bm\delta_V\in V}+\underbrace{(\bm x_W-\bm x'_W)}_{\bm\delta_W\in W}\\ &=\delta_V+\delta_W\\ \to\ &\delta_V=\delta_W=\bm 0 \end{aligned} $$
逆に $\bm\delta\in V\cap W$ が $\bm\delta\ne\bm 0$ であれば、
$$\begin{aligned}\bm x&=\bm x_V+\bm x_W\\ &=(\bm x_V+\bm \delta)+(\bm x_W-\bm \delta)\\ &=\bm x_V'+\bm x_W' \end{aligned}$$
のように成分分解が一意に定まらない。
成分の値はもう一方の空間に依存する †
成分分解のイメージは下図のようなものになる。
同じベクトル $\bm x$ を
$\begin{aligned}V\end{aligned}$ と $W$ に分解したときの $\bm x_V$ と、
$\begin{aligned}V\end{aligned}$ と $W'$ に分解したときの $\bm x'_V$ とは
一般には異なる値になる。
すなわち、ある部分空間の成分は、その部分空間だけでは決まらずに、他の部分空間の取り方にも依存する。
上で $e$ から $P_{\bm e}$ を求められたのとは違い、$V$ の情報のみから $\bm x_V$ を求めることはできない。
$V$ が2次元の時の成分分解のイメージは次の通り。
直交する空間 †
$V$ の任意の元が、 $W$ の任意の元と直交するとき、 $V$ と $W$ とは直交すると言い $V\perp W$ と書く。
$V$ のすべての基底ベクトルが、
$W$ のすべての基底ベクトルと直交することと同義。
注意点として、例えば $xy$ 平面からなる空間 $V_{xy}$ と $yz$ 平面からなる空間 $V_{yz}$ とは図形的には直交しているが、 $y$ 軸上のベクトル $\bm v=(0,1,0)$ は $\bm v\in V$ かつ $\bm v\in W$ であり、 当然 $\bm v\perp \bm v$ は成り立たないので、$V$ と $W$ は直交する空間とは呼ばない。
$V\perp W$ なら $V\cap W=\{\bm 0\}$ である。すなわち一次独立でもある。
直交直和 $V \oplus W$ †
$V\perp W$ の時 $V + W$ を $V$ と $W$ の「直交直和」であるといい、
$$\begin{aligned}V+W=V \oplus W\end{aligned}$$
と書く。当然、直交直和は直和でもある。
このとき、$V,W$ の正規直交基底を合わせると $V \oplus W$ の正規直交基底となる。
∵$V$ の基底ベクトルは $W$ の基底ベクトルと直交する
直交直和の成分分解 †
直交直和の成分分解は簡単である。$\{\,\bm v_k\},\{\,\bm w_k\,\}$ を正規直交基底とすると、
$$\begin{aligned} \bm x&=\underbrace{\sum_{k=1}^n c_{k}\bm v_{k}}_{\,\bm x_V} { }+\underbrace{\sum_{k=1}^m d_{k}\bm w_{k}}_{\,\bm x_W}\\ &=c_k\bm v_k+\underbrace{\sum_{k'\ne k}^n c_{k'}\bm v_{k'}+\sum_{k'=1}^m d_{k'}\bm w_{k'}}_{\perp\,\bm v_k} \end{aligned}$$
のように、$\bm c_k\bm v_k$ を取り出せば、残りの部分は $\bm v_k$ と直交するから、 $\bm c_k\bm v_k$ は $\bm x$ の $\bm v_k$ 方向成分である。
これは上で定義した1次元射影演算子 $P_{\bm v_k}$ を使って $c_k\bm v_k=P_{\bm v_k}\bm x$ と書けるから、
$$\begin{aligned} \bm x_V &=\underbrace{\sum_{k=1}^n P_{\bm v_k}}\bm x\\ &=\ \ P_V\ \ \bm x \end{aligned}$$
すなわち、
$$\begin{aligned}P_V=\sum_{k=1}^n P_{\bm v_k}\end{aligned}$$
が $V\oplus W$ から $V$ への射影演算子となる。
数ベクトルに対しては上で見たとおり
$$\begin{aligned}P_V=\sum_{k=1}^n \bm v_k\bm v_k^\dagger\end{aligned}$$
である。
射影演算子は $V$ の情報だけから定まり、 $W$ に依存しないことに注意せよ。
エルミート演算子の和はエルミート演算子になるから、 $P_{\bm v_k}$ の和である $P_V$ もエルミートである。
(空間が直交しない一般の直和の場合にも「逆基底」を考えることにより、 直交直和の場合とそっくりな形に射影演算子を表すことが可能であるが、ここでは省略する。 → 発展:線形代数II/非直交基底の成分分解)
直交補空間 †
全体空間 $U$ が $U=V\oplus W$ と表されるとき、 $W$ を $V$ の「直交補空間」と呼び、$W=V^\perp$ と書く。
ある線形空間 $V$ に対してその直交補空間は一意に定まる。
$$\begin{aligned}V^\perp=\{\,\bm x\in U\,|\,\forall\bm y\in V,(\bm x,\bm y)=0\,\}\end{aligned}$$
つまり全体集合を、ある空間と、それに直交する補空間と、に分解することはいつも可能である。
あるベクトル $\bm x$ を $\bm e$ に平行な成分 $\bm x_\parallel$ と垂直な成分 $\bm x_\perp$ に分ける問題は、それぞれ線形空間 $V=\{\,\bm p=t\bm e\,|\,t\in K\,\}$ とその直交補空間 $V^\perp$ の成分への分解を表わしていたことになる。
一方、全体空間 $U$ を $U=V\dot + W$ と表せるとき、 $W$ を $V$ の(単なる)「補空間」と呼ぶ。 ある空間の直交補空間が一意に決まるのに対して、 補空間にはさまざまな取り方がある。
直交射影演算子の性質 †
$P_V$ が $V$ への直交射影演算子であるというのは、
任意の $\bm x$ に対して $P_V\bm x=\bm x_\parallel\in V$ かつ $\bm x-P_V\bm x=\bm x_\perp\in V^\perp$ であるというのと同値である
このとき、
- $\bm x\in V$ のとき $P_V\bm x=\bm x$
- $\bm x\in V^\perp$ のとき $P_V\bm x=\bm 0$
- $E=P_V+P_{V^\perp}$ ← ∵$\bm x=P_V\bm x+P_{V^\perp}\bm x=\bm x_\parallel+\bm x_\perp$
- $P_V^2=P_V$ あるいは $P_V(E-P_V)=O$
∵ $P_V\bm x\in V$ だから、$P_V^2\bm x=P_V\bm x$ - これは、$P_{V^\perp}=E-P_V$ であり、$P_VP_{V^\perp}=O$ であることからも理解できる
- またここから、$P_V$ の固有値は $\lambda^2=\lambda$ を満たす、すなわち $\lambda=0,1$ であることが分かる。
- 任意の $\bm x\in V$ が固有値 $1$ に対する固有ベクトル
- 任意の $\bm x\in V^\perp$ が固有値 $0$ に対する固有ベクトル
また、計量線形空間に定義されたある線形変換 $P$ が直交射影演算子となる為の必要十分条件は $PP = P$ かつ $P^\dagger=P$ である → その証明
例 †
$\mathbb R^3$ の部分空間として $\bm a=\begin{pmatrix}1\\2\\3\end{pmatrix},\bm b=\begin{pmatrix}-1\\0\\1\end{pmatrix}$ で張られる空間 $V=\big[\bm a,\bm b\big]\subset \mathbb R^3$を考える。
(1) $\mathbb R^3$ から $V$ への直交射影演算子を求めよ。
(2) 直交補空間 $V^\perp$ に正規直交基底を定めよ。
解答 (1) †
$\bm a,\bm b$ から正規直交基底を作る。
$\bm b$ と垂直なのは $\begin{pmatrix}s\\t\\s\end{pmatrix}$ の形のベクトルであることに注意して、 $\bm c=\bm a-\bm b=\begin{pmatrix}2\\2\\2\end{pmatrix}$ とすれば これは $V$ 内にあり $\bm b$ と垂直なベクトルである。
これらを正規化すれば、
$$\begin{aligned}\bm e_1=\frac{1}{\sqrt 2}\begin{pmatrix}-1\\0\\1\end{pmatrix}, \bm e_2=\frac{1}{\sqrt 3}\begin{pmatrix}1\\1\\1\end{pmatrix}\end{aligned}$$
として正規直交基底が得られる。
したがって、求める射影演算子は
$$\begin{aligned} P_V&=\bm e_1\bm e_1^\dagger+\bm e_2\bm e_2^\dagger\\ &= \frac{1}{2}\begin{pmatrix}-1\\0\\1\end{pmatrix}\begin{pmatrix}-1&0&1\end{pmatrix} {}+\frac{1}{3}\begin{pmatrix}1\\1\\1\end{pmatrix}\begin{pmatrix}1&1&1\end{pmatrix}\\ &= \frac{1}{2}\begin{pmatrix}1&0&-1\\0&0&0\\-1&0&1\end{pmatrix} {}+\frac{1}{3}\begin{pmatrix}1&1&1\\1&1&1\\1&1&1\end{pmatrix}\\ &= \frac{1}{6}\begin{pmatrix}5&2&-1\\2&2&2\\-1&2&5\end{pmatrix} \end{aligned}$$
各射影演算子がエルミート(実数行列では対称)になっていることにも注目せよ。
解答 (1) 別解 †
$\bm b,\bm a$ からシュミットの直交化を用いて正規直交系を作る。
$\bm e_1=\frac{1}{\|\bm a\|}\bm a=\frac{1}{\sqrt 14}\begin{pmatrix}1\\2\\3\end{pmatrix}$
$$\begin{aligned} \bm f_2 &=\bm b-(\bm e_1,\bm b)\bm e_1\\ &=\begin{pmatrix}-1\\0\\1\end{pmatrix} {}-\frac{1}{14}\cdot 2\cdot\begin{pmatrix}1\\2\\3\end{pmatrix}\\ &=\frac{1}{7}\begin{pmatrix}-8\\-2\\4\end{pmatrix} =\frac{2}{7}\begin{pmatrix}-4\\-1\\2\end{pmatrix} \end{aligned}$$
$$\begin{aligned} \bm e_2=\frac{1}{\|\bm f_2\|}\bm f_2=\frac{1}{\sqrt{21}}\begin{pmatrix}-4\\-1\\2\end{pmatrix} \end{aligned}$$
$$\begin{aligned} P_V&= \frac{1}{14}\begin{pmatrix}1\\2\\3\end{pmatrix}\begin{pmatrix}1&2&3\end{pmatrix}+ \frac{1}{21}\begin{pmatrix}-4\\-1\\2\end{pmatrix}\begin{pmatrix}-4&-1&2\end{pmatrix}\\ &=\frac{1}{14}\begin{pmatrix}1&2&3\\&4&6\\&&9\end{pmatrix}+ \frac{1}{21}\begin{pmatrix}16&4&-8\\&1&-2\\&&4\end{pmatrix}\\ &=\frac{1}{42}\begin{pmatrix}3+32&6+8&9-16\\&12+2&18-4\\&&27+8\end{pmatrix}\\ &=\frac{1}{42}\begin{pmatrix}35&14&-7\\&14&14\\&&35\end{pmatrix}\\ &=\frac{1}{6}\begin{pmatrix}5&2&-1\\2&2&2\\-1&2&5\end{pmatrix}\\ \end{aligned}$$
射影演算子はエルミートになるため、左下部分の計算は省略した。
$P_V$ の形は正規直交基底の取り方によらないことに注目せよ。
解答 (2) †
$\mathbb R^3$ が3次元、$V$ が2次元なので、$V^\perp$ は1次元となる。
$\bm e_1,\bm e_2$ に垂直なベクトルを1つ挙げれば例えば、$\begin{pmatrix}1\\-2\\1\end{pmatrix}$
したがって、
$$\begin{aligned}V^\perp=\Big[\begin{pmatrix}1\\-2\\1\end{pmatrix}\Big]\end{aligned}$$
である。正規直交基底はこれを正規化して、
$$\begin{aligned}\Big\{\frac{1}{\sqrt 6}\begin{pmatrix}1\\-2\\1\end{pmatrix}\Big\}\end{aligned}$$
このとき、
$$\begin{aligned} P_{V^\perp}&=\frac{1}{6}\begin{pmatrix}1\\-2\\1\end{pmatrix}\begin{pmatrix}1&-2&1\end{pmatrix}\\ &=\frac{1}{6}\begin{pmatrix}1&-2&1\\-2&4&-2\\1&-2&1\end{pmatrix} \end{aligned}$$
であり、$P_V+P_{V^\perp}=E$ となることが確かめられる。
演習 †
3次元空間に原点を通る平面 $x+y+z=0$ を考える。 この平面への直交射影演算子を求めよ。 またその直交補空間を求めよ。
- ヒント: 次の順に解くと良いでしょう
- 平面の基底を見つける
- 基底を正規直交化する
- 射影演算子を求める
- 直交補空間の基底を求める
解答例 †
まず平面内に基底を取る †
この「原点を通る平面」は2次元部分空間となるから、 平面内に2つの一次独立なベクトルを取れば、 それが平面に対応する線形空間の基底となる。
$x+y+z=0$ を満たせば良いから、例えば、 $\begin{pmatrix}1\\-1\\0\end{pmatrix},\begin{pmatrix}0\\-1\\1\end{pmatrix}$
など、条件を満たすベクトルを「
$x+y+z=0$ を $\begin{pmatrix}1&1&1\end{pmatrix}\begin{pmatrix}x\\y\\z\end{pmatrix}=\bm 0$ の形に書いて、掃出し法により一般解を求めればよい。
とはいえ今の場合は元の $\begin{pmatrix} 1&1&1 \end{pmatrix}$ がすでに階段行列であり掃き出しは終わっている。
掃出しの行えなかった列に対応する $y,z$ をパラメータと見て、
$$\begin{aligned}\begin{cases} x=-y-z\\ y=y\\ z=z \end{cases}\end{aligned}$$
そこで一般解を
$$\begin{aligned}\bm x=y\begin{pmatrix} {}-1\\1\\0 \end{pmatrix}+z\begin{pmatrix} {}-1\\0\\1 \end{pmatrix}\end{aligned}$$
のように書けば、2つのベクトル $\bm b_1=\begin{pmatrix} {}-1\\1\\0 \end{pmatrix}, \bm b_2=\begin{pmatrix} {}-1\\0\\1 \end{pmatrix}$ がこの空間の基底となることが明らかである。
「拡大係数行列にガウスの掃出し法を適用し、
掃出しの行えなかった列に対応する変数をパラメータに取る」
という連立一次方程式の一般解の求め方は常に使える汎用的なものであるから、
必ず身につけておくように。
(そうでないと一般解に含まれるパラメータを1つ忘れるといったミスが起きやすい)
基底を正規直交化する †
これらを直交化するのも暗算で行っても良いが、 シュミットの直交化を使えばどんな場合にも必ず実行できて、
$$\begin{aligned}\bm f_1=b_1=\begin{pmatrix} {}-1\\1\\0 \end{pmatrix}\end{aligned}$$
$$\begin{aligned}\bm e_1=\frac{\bm f_1}{\|\bm f_1\|}=\frac{1}{\sqrt 2}\begin{pmatrix} {}-1\\1\\0 \end{pmatrix}\end{aligned}$$
$$\begin{aligned} \bm f_2&=\bm b_2-\big(\bm e_1,\bm b_2\big)\bm e_1\\ &=\begin{pmatrix} {}-1\\0\\1 \end{pmatrix}-\frac{1}{2}\underbrace{\overline{\begin{pmatrix} {}-1&1&0 \end{pmatrix}}\begin{pmatrix} {}-1\\0\\1 \end{pmatrix}}_{=\,1}\cdot\begin{pmatrix} {}-1\\1\\0 \end{pmatrix}\\ &=\frac{1}{2}\begin{pmatrix} {}-1\\-1\\2 \end{pmatrix} \end{aligned}$$
$$\begin{aligned} \bm e_2=\frac{\bm f_2}{\|\bm f_2\|}=\frac{1}{\sqrt 6}\begin{pmatrix} {}-1\\-1\\2 \end{pmatrix} \end{aligned}$$
途中で、転置されたベクトルの上に線が引いてあるのは 複素共役を取る演算であるが、ここでは実ベクトルなので値は変わらない。
したがって、$V$ の正規直交基底は、
$$\begin{aligned}\{\,\bm e_1,\bm e_2\,\}=\Bigg\{ \ \frac{1}{\sqrt 2}\begin{pmatrix} {}-1\\1\\0 \end{pmatrix},\ \frac{1}{\sqrt 6}\begin{pmatrix} {}-1\\-1\\2 \end{pmatrix}\ \Bigg\} \end{aligned}$$
正規直交基底から射影演算子を作る †
$$\begin{aligned} P_V&=\bm e_1\bm e_1^\dagger+\bm e_2\bm e_2^\dagger= \frac{1}{2}\begin{pmatrix} {}-1\\1\\0 \end{pmatrix}\overline{\begin{pmatrix} {}-1&1&0 \end{pmatrix}}+ \frac{1}{6}\begin{pmatrix} {}-1\\-1\\2 \end{pmatrix}\overline{\begin{pmatrix} {}-1&-1&2 \end{pmatrix}}\\ &=\frac{1}{2}\begin{pmatrix} 1&-1&0\\ {}-1&1&0\\ 0&0&0\\ \end{pmatrix}+ \frac{1}{6}\begin{pmatrix} 1&1&-2\\ 1&1&-2\\ {}-2&-2&4\\ \end{pmatrix}= \frac{1}{6}\begin{pmatrix} 4&-2&-2\\ {}-2&4&-2\\ {}-2&-2&4\\ \end{pmatrix}\\ &= \frac{1}{3}\begin{pmatrix} 2&-1&-1\\ {}-1&2&-1\\ {}-1&-1&2\\ \end{pmatrix} \end{aligned}$$
この $P_V$ に任意の $\bm x$ をかければ、
$$\begin{aligned} P_V\begin{pmatrix} x\\y\\z \end{pmatrix}= \frac{x}{3}\begin{pmatrix} 2\\-1\\-1 \end{pmatrix}+ \frac{y}{3}\begin{pmatrix} {}-1\\2\\-1 \end{pmatrix}+ \frac{z}{3}\begin{pmatrix} {}-1\\-1\\2 \end{pmatrix} \end{aligned}$$
となるが、右辺に現れる3つのベクトルはすべて $x+y+z=0$ を満たしており、 確かに $P_V\bm x\in V$ となることが確認できる。
直交補空間を見つける †
直交補空間 $V^\perp$ は、$V$ の任意の元と直交するベクトルを集めた集合である。
$$\begin{aligned} V^\perp=\{\,\bm x\,|\,\forall\bm y\in V,(\bm x,\bm y)=0\,\} \end{aligned}$$
$\bm y\in V$ は $\bm y=y_1\bm e_1+y_2\bm e_2$ と表せるから、
$(\bm x,\bm y)=0$ は $y_1(\bm x,\bm e_1)+y_2(\bm x,\bm e_2)=0$ を表し、 任意の $\bm y$ すなわち任意の $y_1,y_2$ についてこれが成り立つには、
$$\begin{aligned}(\bm x,\bm e_1)=(\bm x,\bm e_2)=0\end{aligned}$$
が必要十分条件となる。すなわち、
$$\begin{aligned} V^\perp=\{\,\bm x\,|\,\bm x\perp\bm e_1\ \mathrm{and}\ \bm x\perp\bm e_2\,\} \end{aligned}$$
$V$ のすべての基底と直交するベクトルを集めた集合が $V^\perp$ である。
$$\begin{aligned}\begin{cases} {}-x+y=0\\ {}-x-y+2z=0 \end{cases}\end{aligned}$$
の係数行列を同値変形して、
$$\begin{aligned}\begin{pmatrix} {}-1&1&0\\ {}-1&-1&2 \end{pmatrix}\sim \begin{pmatrix} 1&-1&0\\ 0&-2&2 \end{pmatrix}\sim \begin{pmatrix} 1&-1&0\\ 0&1&-1 \end{pmatrix}\sim \begin{pmatrix} 1&0&-1\\ 0&1&-1 \end{pmatrix} \end{aligned}$$
すなわち、$\begin{cases} x-z=0\\ y-z=0 \end{cases}$
掃出せなかった列に対応する $z$ をパラメータとすれば、
$$\begin{aligned}\bm x=z\begin{pmatrix} 1\\1\\1 \end{pmatrix} \end{aligned}$$
すなわち $V^\perp$ の正規直交基底は $\Bigg\{\ \frac{1}{\sqrt 3}\begin{pmatrix} 1\\1\\1 \end{pmatrix}\ \Bigg\}$
そもそも $V$ の定義に現れた条件式 $x+y+z=0$ は、 $\Big(\ \bm x,\ \begin{pmatrix}1\\1\\1\end{pmatrix}\ \Big)=0$ と同値であるから、
$V^\perp$ が $\begin{pmatrix}1\\1\\1\end{pmatrix}$ に平行な1次元空間となることは当然のこととも言える。
一般化 †
以上の話は3つ以上の部分空間がある場合にも拡張できて、以下の通りである。
| 交空間 | $V_1\cap V_2\cap \dots\cap V_r$ | 全空間の共通部分 |
| 和空間 | $V_1+V_2+\dots+V_r$ | 一般には一次従属な空間たちを内包する空間 |
| 直和 | $V_1\dot +V_2\dot +\dots\dot +V_r$ | 一次独立な空間たちの和空間 |
| 直交直和 | $V_1\oplus V_2\oplus \dots\oplus V_r$ | 直交する空間たちの和空間 |
たとえば $V_1\cap V_2\cap V_3\cap V_4=(((V_1\cap V_2)\cap V_3)\cap V_4$ などの意味であるが、これらの演算子には結合法則や交換法則が成り立ち、$(V_1\oplus V_2)\oplus V_3=V_1\oplus (V_2\oplus V_3)$, $V_1\oplus V_2=V_2\oplus V_1$ などとなる。
$\cap$ や $+$ が複数の部分空間から新しい部分空間を作る演算子であるのに比べて、 $\dot +$ や $\oplus$ は 「線形空間同士の演算」 ではなく、 和空間を形成する空間が特殊な条件を満たすことを表現しているに過ぎない。
この違いに注意せよ。
質問・コメント †
誤植 †
通りすがり? ()
成分分解の一意性
δ∈V∩W
- ご指摘ありがとうございます、おっしゃる通りでした。早速修正いたしました。 -- 武内 (管理人)?
添付ファイル: