前の単元 <<<
線形代数II
>>> 次の単元
線形写像の行列表現 †
線形写像
を考える。ただし、
すなわち
に対して
の基底
の基底
を考えれば、
や
の表現を定められる。
これらの関係は図のようになる。
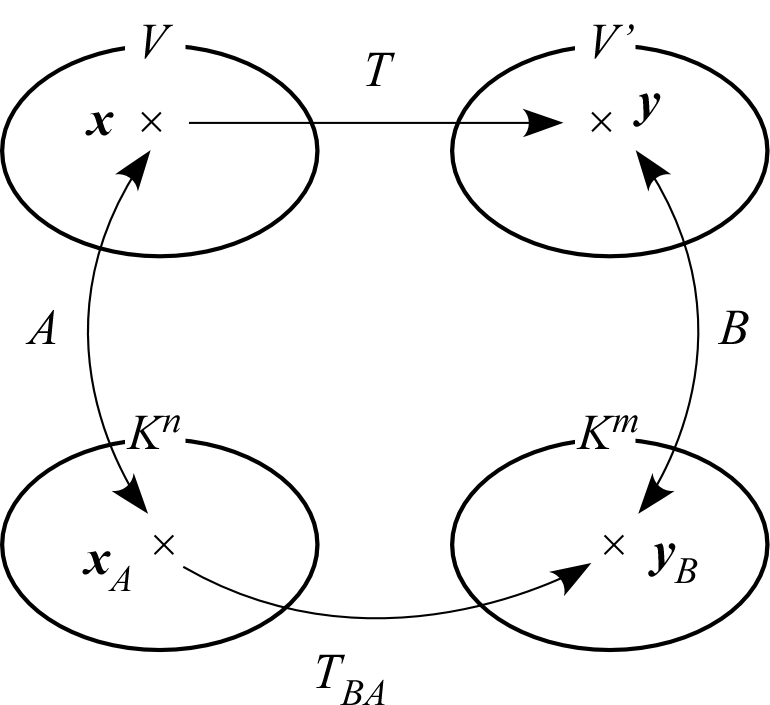
、
、
はそれぞれ線形写像なので、
それらの合成写像である
も線形写像となる。
したがって、
行列
を用いて、
と書ける。
を、線形写像
の行列表現と呼ぶ。
$T_{BA}$ の具体的な形 †
基底
の
番目のベクトル
を移した
の、基底
に対する表現
を考えると良い。
の座標
に対する表現は
であるから、
と置けば、
すなわち、
線形写像の行列表現は、
元となる空間の基底ベクトルに線形写像を施して、
先となる空間の基底で表現したものを列ベクトルとする。
基底の変換行列との関係 †
先にやった基底の変換行列
は、
上記
を恒等変換
に置き換えた形と等しい(
)
すなわち、
行列表現の基底変換 †
から
および、
から
の基底の変換を考える。
に、
、
を適用すれば、
したがって、
基底変換と階数 †
行列の階数は正則行列のかけ算では変化しないことを1年生で学んだ。
すなわち、
が正則の時、
したがって、線形写像の行列表現の階数も任意の基底変換で保存する。
基底変換の例 †
が
で与えられるものとする。
すなわち、
のとき、
これを、
、
を使って表わせば、
より、
一方、
、
を使って表わせば、
のとき、
より、
より、
また、
より、
より、
これらを用いて、
を確かめられる。
演習 †
が
で与えられる。
(1) 上記の基底
に対する
の表現
、
を求めよ
(2)
から
への変換行列
に対して下記を確かめよ
解答例 †
(1)
のとき、
より、
したがって、
一方、
のとき、
より、
したがって、
(2)
より、
線形変換の場合 †
特に、
つまり
で
のときは、
となり、
と
とは相似である。
正方行列
に対して
であれば
と
とは相似であるという。
相似な行列は、以下のように非常に似た特徴を持つことを1年生で学んだ
→ 相似変換に対するトレース、行列式、固有値の保存
- 固有方程式が等しい
- 固有値が等しい
- 行列式が等しい
- トレース(対角要素の和)が等しい
相似な行列がよく似た特徴を持つのは、
それらが同じ線形写像を異なる基底で表したものに過ぎないためで
あったことが分かる。
線形変換のトレース、デターミナント、固有値 †
すなわち、固有値、行列式(デターミナント)、トレースなどは、
基底の取り方によらない線形変換に固有の特性となっており、
- 線形変換の固有値
- 線形変換のデターミナント
- 線形変換のトレース
を具体的な基底を与えることなく定義できる。
前の単元 <<<
線形代数II
>>> 次の単元
