量子力学Ⅰ/物理量の固有関数
概要 †
前回までに以下を学んだ:
- 量子力学では、古典的な物理量に対応した「演算子」を考える
- 適当な境界条件の下で演算子はエルミートになる。すなわち、
- 固有値は実数になる
- 固有関数で正規直交完全系を作れる
- その境界条件を満たす関数の集合(= 関数空間)に属する任意の関数を展開可能(完全性)
- 展開係数を内積により簡単に求められる(正規直交性)
- そのように展開された、「ある波動関数」で表される状態に対してその物理量を測定したならば、
- 観測結果は必ず固有値の1つとなる
- その固有値が得られる確率は、展開係数の絶対値の二乗に比例する
- すなわち、その波動関数が固有関数の1つでない限り、測定結果は確率的にしか予想できない
ここでは、いくつかの物理量演算子の固有関数がどのような形となるかを実際に調べ、 上記を復習するとともに、特に演算子が連続的な固有値を持つ場合の正規直交完全性について学ぶ。
ここで出てくる「正規直交完全な関数系」は、量子力学だけでなく、幅広い分野で使われる非常に重要なものであるため、しっかりと学んでおこう。
目次 †
ハミルトニアン †
演習:箱の中の自由粒子 = 正弦級数 †
箱の中の自由粒子に対して、ハミルトニアンの固有関数は正弦関数となることを見た。
ただし
この関数系は という境界条件の下で正規直交完全系を為す。
(1) のとき、 を示せ(直交性)。
(2) のとき、 を示せ(正規性)。
(3) のとき、
を の形に展開せよ(完全性)。
解説 †
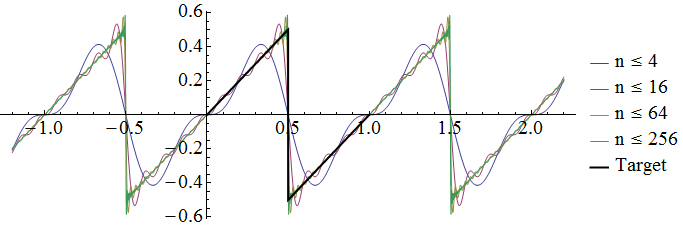
(3) の与式は下図で Target として示したように に不連続点を持つが、 このような関数に対しても上記の無限級数は収束する。
この様子を見るために、展開係数を までで打ち切った場合の関数形を示した。 次数が高くなるに従い、より正確に元の関数を表わしていることが分かる。
グラフからも分かるように、展開後の式は定義域を拡大すれば周期 の周期関数となる。
上記の関数系は整数 に対して を満たす周期 の周期関数について完全系をなすと考えることもできる。
もし境界条件にある の部分を取り去って、 すなわち単なる周期的境界条件とすると、固有関数には正弦関数 sin だけでなく余弦関数 cos も現れる。 任意関数を sin/cos により展開した形は正弦級数展開として知られる。
以上の話は、固有値が離散的になる場合の典型的な性質を表しており、他のケースについてもほぼ同じ話が成り立つ。
例えば調和振動子に対するハミルトニアンの固有関数はエルミート多項式に指数関数をかけた形で与えられたが、このときも異なる固有値に対する固有関数は常に直交し、正規化するだけで正規直交完全系が得られた。ただしこちらの「完全性」は、「無限遠でゼロになる関数すべてが作る空間」に対するものとなる。どのような関数空間において固有関数を求めたかにより、どの範囲の関数に対する完全系が得られるかが決まるのである。無限遠でゼロとなるような任意の関数を調和振動子の時間によらないシュレーディンガー方程式の解で展開することができ、その展開係数の絶対値の二乗は、その関数に対してエネルギーを測定した結果に期待される確率分布を与える。
どちらもまったく同じ話になっていることを理解せよ。
同時固有関数 †
自由な粒子のハミルトニアン演算子に対する固有値問題は、
であるが、実はこれは運動量演算子の固有値問題
が解ければ
のように解けてしまう。
すなわち自由粒子に対しては、運動量の固有関数はハミルトニアンの固有関数にもなっている。 このような固有関数を「同時固有関数」と呼ぶ。
先に、2つのエルミート演算子 の積 がエルミートになるとすれば、 は可換でなければならない ことを証明したが、
逆に演算子 が可換であるとき 、 はエルミートになり、 と の同時固有関数のみで正規直交完全系( ~ 基底)を作れることを 証明できる。
このときエルミート演算子 の固有値は の固有値と の固有値の積となる。( かつ であれば、 は当然)
運動量 = フーリエ変換 †
以下では運動量や位置の演算子を例として、連続的な固有値が得られる場合に固有関数の正規直交性をどのように考えたらいいかについて学ぶ。
まず、運動量に対する固有値問題は
3成分をまとめて書けば、
となる。すなわち、
と書けて、この固有関数は
である。
この固有関数を規格化したら、正規直交完全系が得られるだろうか?
完全性を議論するにはまず関数空間を定義しなければならないが、 ここでは全空間にわたり絶対値が有界であるような関数を集めた空間を考える。 (本当はもっと広い空間でよいがまずは簡単のため)
するとまず、波数 $\bm k$ は実数でなければならないことが分かる。 $\bm k$ に虚数部があれば正か負の遠方で関数の絶対値が無限大に発散してしまうからだ。
固有値 $\bm k$ が実数に限られるというのは良い傾向ではあるのだが、それだけですべてがうまく行くかというと・・・
規格化? †
井戸型ポテンシャルのように系が有限体積の場合には通常通りの規格化ができるが、 無限に広がる自由空間における平面波を考えるとこの関数のノルムは
のように発散してしまい、規格化することができない。
直交性? †
直交関係についても
のように、あと一歩のところで一筋縄ではいかない($k=k'$ で大きくなって、$k\ne k'$ で小さくなるのは傾向としてはあってる)。
この発散や不定の原因は積分範囲が無限であり、固有値が連続であるところにある。
そこで、積分範囲が有限で、固有値が離散的である場合に戻り、それを無限に広げる形で理解していくことにする。(応用数学で複素フーリエ展開からフーリエ変換を導いたことがあれば、それをなぞる形で話が進む)
複素フーリエ展開 †
の範囲で定義された なる「周期境界条件」を満たす関数空間に
を定義する。ただし、 は任意の整数である。
これらは、自由な粒子に対する一次元運動量演算子とハミルトニアン演算子の同時固有関数であり、正規直交完全系をなす。 (「周期的境界条件」は数学的に扱いやすいために様々な問題を解く際に活用される)
正規直交性:
完全性:同じ周期境界条件を満たす任意の関数 を、
ただし、
と展開できる。
この展開は複素フーリエ級数展開と呼ばれ、量子力学以外でも広い範囲の応用がある。 (係数を求める積分で $f(x)$ にかかる指数関数の肩に負号が付いているのは、内積では左側の関数の複素共役をとる必要があったことに由来している)
上で出てきた正弦級数も同じ空間に対する正規直交完全系であり、両者の間の基底変換はユニタリー変換となる。
フーリエ変換 †
複素フーリエ展開において とすると周期がなくなり、任意の有界関数を展開可能になる。 このとき と書けば、 であるから波数は の整数倍に離散化しているが、 のとき となって は連続値を取れるようになる。
ただし、 と置いた。一方、
より、
を得る。
の
から
への変換はフーリエ変換、
の
から
への変換は逆フーリエ変換と呼ばれ、
非常に幅広い応用がある。
量子力学や線形代数以外の分野では と書いて
のように定義することも多い。
ということで、自由粒子に対する運動量の固有関数により様々な関数を展開可能であることが分かった。 (これがどういう関数空間で完全化を議論するのはこの授業の範囲外 → Wikipedia:シュワルツ超函数#緩増加超函数とフーリエ変換)
このとき展開のパラメータ $k$ は連続となるため、シグマではなく積分の形での展開となる。 展開係数が内積で求まっているということは、「正規直交性」も成り立っているはずなのであるが・・・
ディラックのデルタ関数 †
フーリエ変換の公式に逆フーリエ変換の公式を代入すれば、
ここで、式中に示した括弧内を と書けば、この関数
は任意の に対して
を満たすことが分かる。
この関数の形状を思い浮かべるために、 の積分範囲を に制限した関数 を についてプロットした。
式の形から明らかなように、この振動する関数の振幅は のように に反比例するが、この包絡線は を変えても変化しない。一方で、振動周期は の増加に伴い短くなっていく。
においては、 の値によらず となるため、 に比例して は大きな値を取る。
では異なる に対して の位相が異なった物となるために 互いに打ち消し合い、積分範囲を増やしても値は大きくならない。
その結果、積分範囲 を大きくしていくと共に は正の無限大に発散し、 においてはゼロの周りを振動する周期が無限小に短くなる。 このとき、ゼロを含まない任意の範囲 で を積分した結果はゼロとなるため、実質的に とみなせる。
上では $k\ne 0$ に対するデルタ関数の値が「不定」になるとしたにもかかわらず、ここでは「ゼロ」としていることに注意せよ。デルタ関数は のように積分して初めて意味を持つような使い方をすることになるため、「積分した結果」がゼロとみなせるなら、「デルタ関数自身」をゼロとみなして構わない、という意味である。*1専門的には wikipedia:シュワルツ超函数(http://ja.wikipedia.org/wiki/%...) のテスト函数として同値である、ということ
この はディラックのデルタ関数と呼ばれ、 以下のようにクロネッカーのデルタの連続変数版と見なせる性質を持つ。
はステップ関数と呼ばれる
運動量の固有関数の規格化 †
運動量の固有関数を確率密度関数として規格化することはできないが、 上で見たとおり、
であるから、
と置くことにより、
|
|
として、正規直交系としての規格化が可能である。
連続固有値の際の正規直交性はこのように、デルタ関数を用いて表わされることになる。
右に書いた離散固有値の場合との類似性に注目せよ。違いは以下の2点だけである。
- クロネッカーのデルタがディラックのデルタ関数になった
- $n$ に対する和で書かれていたところが $k$ に対する積分になった
このように、連続固有値に対する固有関数は単体では規格化できないため物理的な意味を持たないものの、 規格化された別の波動関数を展開し、物理量の確率分布を得るための正規直交完全系として使い道を見出すことができる。
3次元の場合には、
と置けば、
となる。
離散固有値と連続固有値とが両方現れる系 †
有限のエネルギー障壁に閉じ込められた箱の中の自由粒子に対するエネルギー固有値は、 エネルギー障壁の高さを $V_0$ として、
- $\varepsilon<V_0$ は離散固有値に
- $V_0<\varepsilon$ は連続固有値に
なる。そのような場合にも、これらの固有値に対応する固有関数をすべて合わせた関数系は完全になり、 関数空間内の任意の関数 $f(x)$ を展開した形は、
$$ \begin{aligned} f(x)&=\underbrace{\sum_{n=1}^{\varepsilon_n<V_0}F_n\varphi_n(x)}_{\text{離散部分}}+ \underbrace{\int_{V_0}^{\infty}F(\varepsilon)\varphi_{\varepsilon}(x)\,d\varepsilon}_{\text{連続部分}}\\ \end{aligned} $$
のようになる。
位置 = ディラックのデルタ関数 †
位置の演算子は であるから、 その固有値問題は
の形になる。変形して、
より、 において でなければならないことが分かる。
残るは の1点の値のみであるから この値は規格化によって決めれば良いのであるが、 運動量の場合と同様に、ここでも固有値が連続であるため その規格化は正規直交条件により行うことになる。
正規直交性は、
この関係は と置けば満たされる。
このとき任意の関数 を で展開すれば、
となり、展開係数は 自身となる。
角運動量 = 球面調和関数 †
古典論において、原点を中心とした角運動量は として定義された。
量子論においても角運動量演算子は
のように定義される。例えば
であるから、
また、
に対して、
であるから、
すなわち、全角運動量の大きさの2乗と 軸周りの角運動量との同時固有状態はあり得るが、 軸周りの角運動量と 軸周りの角運動量の同時固有状態は $\hat l_z\phi(\bm r)=0$ の空間内にしか存在しないことになる・・・これは $\hat l_z$ に対する固有値 0 の固有関数でもあって・・・$l_x=l_y=l_z=0$ すなわち $l^2=0$ となる「$s$ 状態」のみが $\hat l_x,\hat l_y,\hat l_z$ の同時固有状態となる。
および
の同時固有関数は球面調和関数と呼ばれるが、
詳細は 量子力学Ⅰ/球面調和関数 にて学ぶ。
また、一般的な角運動量演算子の固有値については 量子力学/角運動量の固有値 に記述した。
質問・コメント †
デルタ関数のグラフについて †
()
2つ目のグラフの3つの曲線はそれぞれ、|k|<200,|k|<50,|k|<10ではなくて、|a|<200,|a|<50,|a|<10ではないでしょうか?
- ありがとうございます、ご指摘の通りでした。修正いたしました。 -- 武内(管理人)?
演習問題の解答について †
()
(3)の解答について、n=2mの時、Cn=(-1)^m*2^(1/2)*(nπ)^(-1)ではないでしょうか?
- ありがとうございます、ご指摘の通りでした。修正いたしました。 -- 武内(管理人)?
添付ファイル: