箱の中の自由粒子/メモ
目次 †
概要 †
量子力学Ⅰ/箱の中の自由粒子 のページの補足です。
演習:1次元の箱の中の自由粒子 †
解答 †
(1) 箱の内部では $V(x)=0$ であるから、シュレーディンガー方程式は
$$ {}-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}\varphi(x)=\varepsilon\varphi(x) $$
(2) 与式を代入すれば、
$$ {}-\frac{\hbar^2}{2m}\frac{d}{dx}(ikAe^{ikx}-ikBe^{-ikx})=\varepsilon\varphi(x) $$
$$ {}-\frac{\hbar^2}{2m}(-k^2Ae^{ikx}-k^2Be^{-ikx})=\varepsilon\varphi(x) $$
$$ \frac{\hbar^2k^2}{2m}\varphi(x)=\varepsilon\varphi(x) $$
常に $\varphi(x)=0$ では解にならないから $\frac{\hbar^2k^2}{2m}=\varepsilon$ すなわち $k=\frac{\sqrt{2m\varepsilon}}{\hbar}$ と求まる。
(3) $V(x)=+\infty$ の点で $\varphi(x)\ne 0$ であれば右辺は有限値、 左辺は $\infty$ となり方程式を満たさないため。
(4) 境界条件は $\varphi(0)=\varphi(a)=0$ であるから、
$$\varphi(0)=A+B=0\ \text{すなわち} B=-A$$
$$\varphi(a)=A(e^{ika}-e^{-ika})=2iA\sin(ka)=0$$
$A=0$ では解にならないから $\sin(ka)=0$ すなわち $n$ を任意の整数として $ka=n\pi$ つまり
$$k=k_n=n\pi/a$$
であるときに限り境界条件を満たす。
ここで、$n=0$ は $k=0$、 すなわち $\varphi$ が定数となり、境界条件から $\varphi(x)=0$ となってしまい、解にはならない。 また、$n$ と $-n$ とは解の符号が変わるのみであるから、 独立な解にならない。
そこで、$n$ を自然数に限ることにより、異なる $n$ がそれぞれ独立な固有関数を表わす。
(5) (2) の式を $\varepsilon$ について解くことにより、
$$\varepsilon_n=\frac{\hbar^2 k_n^2}{2m}=\frac{\hbar^2 \pi^2}{2ma^2}n^2$$
ここまでで、境界条件により $k$ および $\varepsilon$ が飛び飛びの実数値しか取れないことが分かった。
(6) 固有関数は $0\le x\le a$ において $\varphi_n(x)=C\sin(n\pi x/a)$ の形になり、井戸の外では $0$ となる。
$$ \begin{aligned} \int_{-\infty}^\infty|\varphi(x)|^2\,dx &=\int_0^a\big|C\sin(n\pi x/a)\big|^2\,dx\\ &=|C|^2\int_0^a\frac{1-\cos(2n\pi x/a)}{2}\,dx\\ &=\frac{|C|^2}{2}\Big[x-\frac{a}{2n\pi}\sin(2n\pi x/a)\Big]_0^a\\ &=\frac{a|C|^2}{2}\\ &=1\\ \end{aligned} $$
より、例えば $C=\sqrt{2/a}$ と置けば良く、
$$\varphi_n(x)=\begin{cases} \sqrt{2/a}\sin(n\pi x/a)&(0\le x\le a)\\ 0&(x<0, a<x) \end{cases}$$
を得る。
この波動関数に、「絶対値が1となる任意の複素定数」を掛けてもやはり規格化された解を与えることに注意せよ。
(7) $\psi_n(x,t)=e^{-i\omega_n t}\varphi_n(x)$
ただし、$\hbar\omega_n=\varepsilon_n=\frac{\hbar^2 \pi^2}{2ma^2}n^2$ より、
$$\psi_n(x,t)=\begin{cases} \sqrt{\frac{2}{a}}\exp\Big(-i\underbrace{\frac{\hbar n^2\pi^2}{2ma^2}}_{\omega_n}t\Big)\sin\Big(\underbrace{\frac{n\pi}{a}}_{k_n} x\Big)&(0\le x\le a)\\ 0&(x<0, a<x) \end{cases}$$
(8)
$$ \begin{aligned} \overline x&=\int_{-\infty}^\infty\psi_n^*(x,t)x\psi_n(x,t)dx\\ &=\int_0^a\varphi_n^*(x)\cancel{e^{i\varepsilon_n t/\hbar}}x\varphi_n(x)\cancel{e^{-i\varepsilon_n t/\hbar}}dx\\ &=\int_0^a\varphi_n^*(x)x\varphi_n(x)dx\\ &=\int_0^a\sqrt{\frac{\,2\,}{a}}\sin\Big(\frac{n\pi}{a} x\Big) \ x\ \sqrt{\frac{\,2\,}{a}}\sin\Big(\frac{n\pi}{a} x\Big)\,dx\\ &=\frac{\,2\,}{a}\int_0^a x\sin^2\Big(\frac{n\pi}{a} x\Big)dx\\ &=\frac{\cancel{\,2\,}}{a}\int_0^a x\,\frac{1-\cos\big(2n\pi x/a\big)}{\cancel{\,2\,}}dx\\ &=\frac{\,1\,}{a}\Big[\frac{1}{2}x^2\Big]_0^a-\frac{1}{\cancel a}\Big[\cancel{\frac{\cancel a}{2n\pi}x\sin\Big(\frac{2n\pi}{a}x\Big)}\Big]_0^a+\frac{1}{2n\pi}\cancel{\int_0^a \sin\Big(\frac{2n\pi}{a}x\Big)dx}\\ &=\frac{\,a\,}{2} \end{aligned} $$
$$ \begin{aligned} \sigma_x^2&=\int_{-\infty}^\infty\psi_n^*(x,t)(x-\overline x)^2\psi_n(x,t)dx\\ &=\frac{\,2\,}{a}\int_0^a \Big(x^2-ax+(a/2)^2\Big)\sin^2\Big(\frac{n\pi}{a} x\Big)dx\\ &=\frac{\cancel{\,2\,}}{a}\int_0^a x^2\,\frac{1-\cos\big(2n\pi x/a\big)}{\cancel{\,2\,}}dx-a\cdot\overline x+\frac{a^2}{4}\cdot 1\\ &=\frac{\,1\,}{a}\Big[\frac{1}{3}x^3\Big]_0^a {}-\frac{\,1\,}{a}\Big[x^2\frac{a}{2n\pi}\,\cancel{\sin(2n\pi x/a)\rule[-0.4em]{0pt}{1.4em}}\ \Big]_0^a {}+\frac{\,1\,}{\cancel{\,a\,}}\int_0^a 2x\,\frac{\cancel{\,a\,}}{2n\pi}\sin(2n\pi x/a)dx-\frac{a^2}{4}\\ &=\frac{\,a^2\,}{12} {}+\frac{1}{2n\pi}\Big[-2x\frac{a}{2n\pi}\cos(2n\pi x/a)\Big]_0^a {}+\frac{\,1\,}{2n\pi}\cancel{\int_0^a \frac{a}{2n\pi}\cos(2n\pi x/a)dx}\\ &=\frac{\,a^2\,}{12}\biggl(1-\frac{6}{n^2\pi^2}\biggr)\\ \end{aligned} $$
3つ目の等号は上記の $\overline x$ の表式と、$\varphi_n(x)$ が規格化されていることを用いた。
$$ \sigma_x=\frac{a}{2}\sqrt{\frac{\,1\,}{3}-\frac{2}{\pi^2}\frac{1}{n^2}} $$
$$ \begin{aligned} \overline p&=\int_0^a\psi_n^*(x,t)\,\frac{\hbar}{i}\frac{\partial}{\partial x}\psi_n(x,t)dx\\ &=-\frac{2i\hbar}{a}\int_0^a \sin\Big(\frac{n\pi}{a} x\Big)\frac{n\pi}{a}\cos\Big(\frac{n\pi}{a} x\Big)dx\\ &=-\frac{in\pi\hbar}{a^2}\int_0^a \sin\Big(\frac{2n\pi}{a} x\Big)dx\\ &=0 \end{aligned} $$
$p^2$ については井戸の両端で二階微分が無限大に発散するため本来は注意が必要である。ここではたまたま、以下の計算で正しい答えが求まる。詳しくは 有限不可さの井戸の極限として求めた結果 を参照のこと。
$$ \begin{aligned} \sigma_p^2&=\int_{-\infty}^\infty\psi_n^*(x,t)\Big(\frac{\hbar}{i}\frac{\partial}{\partial x}-\overline p\Big)^2\psi_n(x,t)dx\\ &=\int_0^a\psi_n^*(x,t)\underbrace{\Big(\frac{\hbar}{i}\frac{\partial}{\partial x}\Big)^2}_{\hat p^2\,=\,2m\hat H}\psi_n(x,t)dx\\ &=2m\varepsilon_n=\Big(\frac{\pi\hbar}{a}\Big)^2n^2 \end{aligned} $$
$$\sigma_p=\frac{\pi\hbar}{a}n$$
波動関数の形:偶関数と奇関数 †
$x=0$ に対して対称なポテンシャルに対するエネルギーの固有関数は必ず偶関数あるいは奇関数の形に書ける。
縮退のない場合、すなわちある固有値 $\varepsilon_k$ に対して一次独立な固有関数が それぞれ1つだけしか無い場合については以下のように簡単に証明できる。
$$\left(-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}+V(x)\right)\varphi_k(x)=\varepsilon_k\varphi_k(x)$$
において、ポテンシャルが原点に対して対称、つまり $V(-x)=V(x)$ とする。
上の式の $x$ を $x\to -x$ と変数変換すると、
$\frac{\partial}{\partial x}\to -\frac{\partial}{\partial x}$、 $\frac{\partial^2}{\partial x^2}\to \frac{\partial^2}{\partial x^2}$、 $V(x)\to V(-x)=V(x)$ より、
$$\left(-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}+V(x)\right)\varphi_k(-x)=\varepsilon_k\varphi_k(-x)$$
を得る。すなわち、$\varphi_k(-x)$ も固有値 $\varepsilon_k$ に属する固有関数である。
縮退していない場合、$\varphi_k(-x)=A\varphi_k(x)$ と書けることになるが、 同様に $\varphi_k(-(-x))=A\varphi_k(-x)$ であるから、
$$\varphi_k(x)=\varphi_k(-(-x))=A\varphi_k(-x)=A^2\varphi_k(x)$$
となって、$A=\pm 1$ でなければならない。
これは $\varphi_k(-x)=\pm\varphi_k(x)$ を意味しており、 エネルギー固有関数が必ず偶関数あるいは奇関数となることを意味している。
以下に見るとおり1次元の束縛状態に関する限り、エネルギー固有値が縮退することはないため、 上記の通り自動的に偶関数あるいは奇関数の固有関数が得られることになる。
1次元の束縛状態が縮退することはない †
時間に依存しないシュレーディンガー方程式は2階の微分方程式であるから、 あるエネルギー値を指定して方程式を解けばその一般解には2つの独立なパラメータが含まれる。
その両方のパラメータを自由に取ることができる場合には2つの独立な固有関数が得られて、 それらは縮退していることになる。
しかし束縛状態では最低限 $|\varphi(\pm \infty)|^2=0$ なる境界条件を満たさなければならないため、 2つのパラメータを独立に決めることができなくなり、結果的に独立なパラメータは1つになってしまう。
さらにそのパラメータは波動関数を規格化する際に絶対値が決まってしまうため、 実質的な自由パラメータは初期位相 $\theta$ のみになってしまう。
以下これを数学的に検証しよう。
1つのエネルギー固有値 $\varepsilon$ に対して2つの固有関数 $\varphi_1(x),\varphi_2(x)$ があったとする。
$$ \begin{aligned} \Big(-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}+V(x)\Big)\varphi_1(x)&=\varepsilon\varphi_1(x)\\ \Big(-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}+V(x)\Big)\varphi_2(x)&=\varepsilon\varphi_2(x) \end{aligned} $$
それぞれ $\varphi_2(x),\varphi_1(x)$ を掛けて辺々引き算すると、
$$ \begin{aligned} {}-\frac{\hbar^2}{2m}\Big(\varphi_2(x)\frac{d^2}{dx^2}\varphi_1(x)-\varphi_1(x)\frac{d^2}{dx^2}\varphi_2(x)\Big)=0 \end{aligned} $$
$$ \begin{aligned} \varphi_2(x)\varphi_1''(x)- \varphi_1(x)\varphi_2''(x)&=\\ \Big(\varphi_2(x)\varphi_1'(x)-\varphi_1(x)\varphi_2'(x)\Big)'&=0 \end{aligned} $$
すなわち、
$$\varphi_2(x)\varphi_1'(x)-\varphi_1(x)\varphi_2'(x)=\mathit{const.}$$
$\varphi_1(\pm\infty)=\varphi_2(\pm\infty)=0$ ならば右辺はゼロでなければならず、
$$\varphi_2(x)\varphi_1'(x)-\varphi_1(x)\varphi_2'(x)=0$$
$$ \begin{aligned} \left(\frac{\varphi_1(x)}{\varphi_2(x)}\right)' &=\frac{\varphi_1'(x)}{\varphi_2(x)}-\frac{\varphi_1(x)\varphi_2'(x)}{\varphi_2(x)^2}\\ &=\frac{\varphi_2(x)\varphi_1'(x)-\varphi_1(x)\varphi_2'(x)}{\varphi_2(x)^2}\\ &=0 \end{aligned} $$
であるから、定数 $A$ を用いて
$$\frac{\varphi_1(x)}{\varphi_2(x)}=A$$
すなわち $\varphi_2(x)\ne 0$ となる点で
$$\varphi_1(x)=A\varphi_2(x)$$
逆に $\left(\varphi_2(x)/\varphi_1(x)\right)'$ から始めれば $\varphi_1(x)\ne 0$ となる点で
$$\varphi_2(x)=B\varphi_1(x)$$
それ以外の点では $\varphi_1(x)=\varphi_2(x)=0$ であるから、 結局全範囲で
$$\varphi_1(x)=A\varphi_2(x)$$
と書け、$\varphi_1(x)$ と $\varphi_2(x)$ は一次従属である。
$\varphi_n(x)$ の運動量分布 †
後に 量子力学Ⅰ/固有値と期待値#y88cc546 や 量子力学Ⅰ/物理量の固有関数#z1c11612 で学ぶように、$\varphi_n(x)$ で表される状態に対して運動量を測定した結果、$\hbar k<p<\hbar (k+dk)$ を満たす運動量が得られる確率 $P\{\hbar k<p<\hbar (k+dk)\}$ は、
$$\varphi_k(x)=\frac1{\sqrt{2\pi}}e^{ikx}$$
に対して、
$$ C_k=\int_{-\infty}^\infty\varphi_k^*(x)\varphi_n(x)dx $$
とするとき、
$$ P\{\hbar k<p<\hbar (k+dk)\}=|C_k|^2dk $$
として求められる。
具体的に計算すると、
$$ \begin{aligned} C_k&=\frac1{\sqrt{\pi a}}\int_0^a e^{-ikx}\sin(n\pi x/a)dx\\ &=\frac1{2i\sqrt{\pi a}}\int_0^a\big(e^{i(-k+n\pi/a)x}-e^{i(-k-n\pi/a)x}\big)dx\\ &=\frac1{2i\sqrt{\pi a}}\bigg[\frac{e^{i(-k+n\pi/a)x}}{i(-k+n\pi/a)}-\frac{e^{i(-k-n\pi/a)x}}{i(-k-n\pi/a)}\bigg]_0^a\\ &=\frac1{2\sqrt{\pi a}}\bigg(-\frac{e^{i(-ka+n\pi)}-1}{-k+n\pi/a}+\frac{e^{i(-ka-n\pi)}-1}{-k-n\pi/a}\bigg)\\ &=\frac1{2\sqrt{\pi a}}\bigg(-\frac{(-1)^ne^{-ika}-1}{-k+n\pi/a}+\frac{(-1)^ne^{-ika}-1}{-k-n\pi/a}\bigg)\\ &=\frac{(-1)^ne^{-ika}-1}{\sqrt{\pi a}}\frac{n\pi/a}{k^2-(n\pi/a)^2}\\ \end{aligned} $$
$$ \begin{aligned} |C_k|^2&=((-1)^ne^{-ika}-1)((-1)^ne^{ika}-1)\frac{n^2\pi a}{(k^2a^2-n^2\pi^2)^2}\\ &=\frac{2n^2\pi a\big(1-(-1)^n\cos ka\big)}{(k^2a^2-n^2\pi^2)^2} \end{aligned} $$
この関数は $n=1$ では $k=0$ を中心に広がるが、 $n>1$ では分母がゼロになる $k=\pm n\pi/a$ 付近に最大値を持つ。 ただし、ピークはそこからわずかに $|k|$ が小さいほうにずれる。
つまり、$n=1$ では $p=0$ が観測される確率が最も高いが、 $n>1$ では $p\sim\pm n\pi\hbar/a$ と観測されることが期待される。
下のグラフでは $n=1,2,3,4,5$ について、$|C_k|^2$ を横軸を $\pi/a$ を単位とした $k$ に対してプロットした。
この $|C_k|^2$ は偶関数なので $\langle k\rangle=0$ となる。一方、$\sigma_k^2=\langle k^2\rangle$ を求めれば、
$$ \begin{aligned} \sigma_k^2&=\langle k^2\rangle=\int_{-\infty}^\infty|C_k|^2k^2dk\\ &=2n^2\pi a\int_{-\infty}^\infty \frac{\big(1-(-1)^n\cos ka\big)k^2}{(k^2a^2-n^2\pi^2)^2}dk\\ &=(2n^2\pi /a^2)\underbrace{\int_{-\infty}^\infty \frac{\big(1-(-1)^n\cos ka\big)k^2a^2}{(k^2a^2-n^2\pi^2)^2}d(ka)}_{\pi/2}\\ &=n^2 \pi^2/a^2 \end{aligned} $$
として、期待通り $\overline {p^2}=n^2\hbar^2 \pi^2/a^2$ の値が得られる(according to Mathematica)。
Plot[Table[
(2 n^2 Pi (1 - (-1)^n Cos[Pi k]))/(Pi^2 k^2 - n^2 Pi^2)^2, {n, 1, 5, 1}] // Evaluate,
{k, -10, 10}, PlotRange -> Full, GridLines -> Automatic]
Integrate[(1 - (-1)^n Cos[k]) k^2/(k^2 - n^2 Pi^2)^2, {k, -Infinity, Infinity}]
(* 微係数がゼロになるところを探す → ピッタリ n Pi / a にはならず少し左にずれる *)
D[(1 - (-1)^n Cos[k a])/(k^2 a^2 - n^2 Pi^2)^2, k] /.
k -> n Pi/a + \[CapitalDelta]k/a // FullSimplify[#, n \[Element] Integers] &
Plot[Table[% (2 n \[Pi] + \[CapitalDelta]k)^3/a, {n, 2, 5}], {\[CapitalDelta]k, -Pi, Pi}]
非定常状態の解 †
LANG:mathematica
Subscript[\[Psi], n_][x_, t_] := Sqrt[2] Exp[I n^2 t] Sin[n Pi x]
\[Psi][x_, t_] :=
1/Sqrt[2] (Subscript[\[Psi], 1][x, t] + Subscript[\[Psi], 2][x, t])
Module[{t = 0},
Show[{
Plot[{
Abs[\[Psi][x, t]]^2, \[Psi][x, t],
Subscript[\[Psi], 1][x, t],
Subscript[\[Psi], 2][x, t]
}, {x, 0, 1},
BaseStyle -> {FontSize -> 18}, ImageSize -> Large,
PlotRange -> {-1.5, 3.5}, PlotStyle -> {Thick, Thick, Thin, Thin},
PlotLegends -> "Expressions"],
Graphics[Text["t = " <> ToString[t], {0.8, 2.8}, {-1, 0}]]
}]
]
ComplexToXY[z_] := {Re[z], Im[z]}
animation = Table[
Grid[{{
Show[{
Plot[{
Abs[\[Psi][x, t]^2], Abs[\[Psi][x, t]],
Abs[Subscript[\[Psi], 1][x, t]],
Abs[Subscript[\[Psi], 2][x, t]]
}, {x, 0, 1},
BaseStyle -> {FontSize -> 18}, ImageSize -> Medium,
PlotRange -> {-1.5, 3.5}, PlotStyle -> {Thick, Thick, Thin, Thin},
PlotLegends -> {
"\[LeftBracketingBar]\[Psi](x,t)\!\(\*SuperscriptBox[\(\[RightBracketingBar]\), \(2\)]\)",
"|\[Psi](x,t)|",
"\[LeftBracketingBar]\!\(\*SubscriptBox[\(\[Psi]\), \(1\)]\)(x,t)\[RightBracketingBar]",
"|\!\(\*SubscriptBox[\(\[Psi]\), \(2\)]\)(x,t)|"
}],
Graphics[Text["t = " <> ToString[t], {0.1, 3.3}, {-1, 0}]]}
]
}, {
Show[{
ParametricPlot3D[
({x, #[[1]], #[[2]]} & /@
ComplexToXY /@ {
a \[Psi][x, t],
a Subscript[\[Psi], 1][x, t],
a Subscript[\[Psi], 2][x, t]}
) // Evaluate, {x, 0, 1}, {a, 0, 1},
PlotPoints -> 40, BaseStyle -> {FontSize -> 18},
ImageSize -> Medium, PlotRange -> {{0, 1}, {-2, 2}, {-2, 2}},
BoxRatios -> {1, 0.5, 0.5}, PlotStyle -> Opacity[0.5], MeshStyle -> None
],
ParametricPlot3D[
({x, #[[1]], #[[2]]} & /@ ComplexToXY /@ {
\[Psi][x, t],
Subscript[\[Psi], 1][x, t],
Subscript[\[Psi], 2][x, t]}
) // Evaluate, {x, 0, 1},
PlotPoints -> 40, BaseStyle -> {FontSize -> 18}, ImageSize -> Medium,
PlotRange -> {{0, 1}, {-2, 2}, {-2, 2}}, BoxRatios -> {1, 0.5, 0.5},
PlotStyle -> {{Thick, Purple}, {Thin, Darker[Yellow]}, {Thin, Darker[Darker[Green]]}}
]}]
}}], {t, 0, 2 Pi, 0.02}
];
Export["oscillation.gif", animation, "GIF"]
Integrate[x Abs[\[Psi][x, t]]^2, {x, 0, 1}] // FullSimplify
Show[{
DensityPlot[
Abs[\[Psi][x, t]^2], {x, 0, 1}, {t, 0, 2 Pi},
BaseStyle -> {FontSize -> 18}, ImageSize -> Large, PlotPoints -> 150,
FrameLabel -> {x, t}, LabelStyle -> Directive[FontFamily -> "Times", FontSize -> 22]
],
ParametricPlot[
{(E^(-2 Im[t]) (9 \[Pi]^2 - 32 Cos[3 t]))/(18 \[Pi]^2), t},
{t, 0, 2 Pi}, PlotStyle -> {Thick, Red}
]
}]
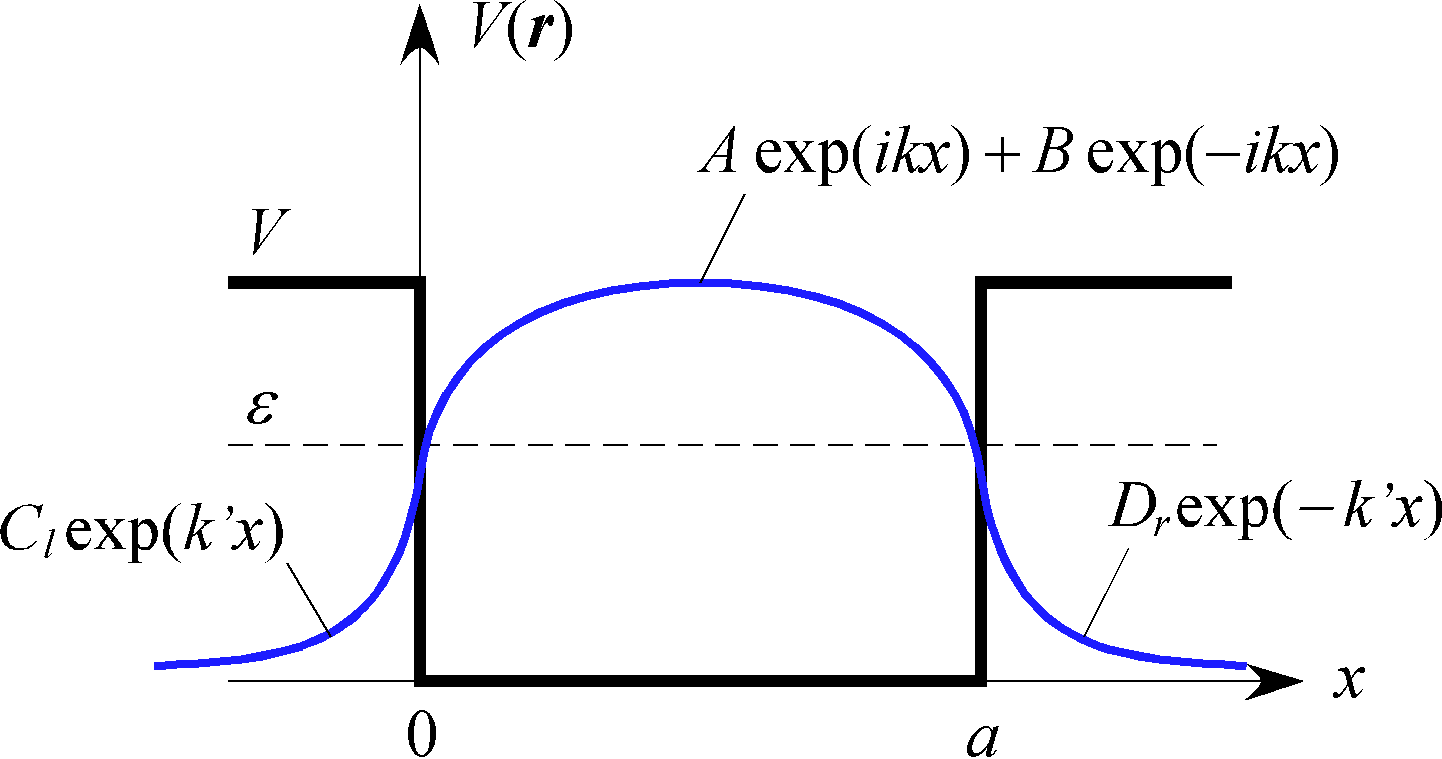
1次元の箱の中の自由粒子(有限ポテンシャル) †
波動関数の微係数の連続性 †
現実的なポテンシャルに対応するシュレーディンガー方程式を満たす波動関数は
- いたる所連続で
- なおかつその一次微分も連続となる
特に、ポテンシャルに有限の飛びを持つ不連続点がある場合にも、 その点の近傍で波動関数はその1次微分まで連続となる。
このことを確かめるため、$V(x)$ が $x=x_0$ において有限の飛びを持つとして、 $x_0$ の近傍 $[x_0-\delta,x_0+\delta]$ で 時間に依存しないシュレーディンガー方程式を積分してみる。
$$\int_{x_0-\delta}^{x_0+\delta}\left(-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}\varphi(x)+V(x)\varphi(x)-\varepsilon\varphi(x)\right)\,dx=0$$
$$\left[\frac{\hbar^2}{2m}\frac{d}{dx}\varphi(x)\right]_{x_0-\delta}^{x_0+\delta} =\int_{x_0-\delta}^{x_0+\delta}\Big(V(x)-\varepsilon\Big)\varphi(x)\,dx$$
$$ \begin{aligned} \frac{\hbar^2}{2m}\Big(\varphi'(x_0-\delta)-\varphi'(x_0+\delta)\Big) &=\overline{\Big(V(x)-\varepsilon\Big)\varphi(x)}\int_{x_0-\delta}^{x_0+\delta}\,dx\\ &=\overline{\Big(V(x)-\varepsilon\Big)\varphi(x)}\cdot 2\delta \end{aligned} $$
ただし、$\overline{\Big(V(x)-\varepsilon\Big)\varphi(x)}$ は積分区間内での $\Big(V(x)-\varepsilon\Big)\varphi(x)$ の平均値である。
もしこの区間で $V(x)$ や $\varphi(x)$ に不連続性があったとしても、 その値が有限である限り、平均値も有限であるため、$\delta\to 0$ の極限では 右辺はゼロとなり、
$$\varphi'(x_0-\delta)-\varphi'(x_0+\delta)\to 0$$
を得る。
すなわち $\varphi'(x)$ は連続であり、当然 $\varphi(x)$ も連続である。
導出過程からも分かるとおり、$V(x)$ が無限大に発散する点ではこの限りではない。
詳しい導出過程 †
$k=\sqrt{2m\varepsilon}/\hbar$、$k'=\sqrt{2m(V-\varepsilon)}/\hbar$ に対して、
- 箱の左: $\varphi_l(x)=C_le^{k'x}$
- 箱の中: $\varphi_m(x)=Ae^{ikx}+Be^{-ikx}$
- 箱の右: $\varphi_r(x)=D_re^{-k'x}$
境界条件は、
- $\varphi_l(0)=\varphi_m(0)$、$\varphi_l'(0)=\varphi_m'(0)$
- $\varphi_m(a)=\varphi_r(a)$、$\varphi_m'(a)=\varphi_r'(a)$
方程式から求めるべきパラメータは $A, B, C_l, D_r, \varepsilon$ の5つ。
式は4つなので1つを除いて値が決まることになる。
ただし方程式の中に周期関数が入っているので複数の解が存在する。
代入すると、
$C_l=A+B$、$k'C_l=ik(A-B)$ より $\frac{A-B}{A+B}=\frac{k'}{ik}$
$Ae^{ika}+Be^{-ika}=D_re^{-k'a}$、$ik(Ae^{ika}-Be^{-ika})=-k'D_re^{-k'a}$ より $\frac{Ae^{ika}-Be^{-ika}}{Ae^{ika}+Be^{-ika}}=-\frac{k'}{ik}$
したがって、
$$-\frac{A-B}{A+B}=\frac{Ae^{ika}-Be^{-ika}}{Ae^{ika}+Be^{-ika}}$$
$$-(A-B)(Ae^{ika}+Be^{-ika})=(A+B)(Ae^{ika}-Be^{-ika})$$
$$A^2e^{i2ka}=B^2$$
$$B=\pm Ae^{ika}$$
これを上の式に代入すれば、
$$C_l=A(1\pm e^{ika})$$
$$D_r=Ae^{k'a}(e^{ika}\pm 1)$$
であり、さらに $k'C_l=ik(A-B)$ より
$$k'(1\pm e^{ika})=ik(1\mp e^{ika})$$
を得る。
$$ \begin{aligned} \varphi_m(x)&=A(e^{ikx}\pm e^{ka}e^{-ikx})\\ &=Ae^{ka/2}(e^{ik(x-a/2)}\pm e^{-ik(x-a/2)})\\ &=2Ae^{ka/2}\frac{e^{ik(x-a/2)}\pm e^{-ik(x-a/2)}}{2}\\ \end{aligned} $$
$$C_l=2Ae^{ka/2}\frac{e^{-ika/2}\pm e^{ika/2}}{2}$$
$$D_r=2Ae^{ka/2}\,e^{k'a}\frac{e^{ika/2}\pm e^{-ika/2}}{2}$$
$$(k'a/2)\frac{e^{-ika/2}\pm e^{ika/2}}{2}=i(ka/2)\frac{e^{-ika/2}\mp e^{ika/2}}{2}$$
より $2Ae^{ka/2}=A'$ と置いて、
[複号の上を取れば]
$$\varphi_l(x)=A'\cos(-ka/2)e^{k'x}$$
$$\varphi_m(x)=A'\cos\big(k(x-a/2)\big)$$
$$\varphi_r(x)=A'\cos(ka/2)e^{-k'(x-a)}$$
$$(k'a/2)\cos(ka/2)=(ka/2)\sin(ka/2)$$
$$ \begin{aligned} \int_{-\infty}^\infty|\varphi|^2dx &=2A'^2\cos^2(-ka/2)\int_{-\infty}^0e^{2k'x}dx {}+A'^2\int_0^a\cos^2(k(x-a/2))dx\\ &=\frac{A'^2\cos^2(ka/2)}{k'}+A'^2\int_0^a\frac{1+\cos(2k(x-a/2))}2dx\\ &=\frac{A'^2\cos^2(ka/2)}{k'}+A'^2\Big(\frac a2+\frac1{2k}\sin(ka)\Big)=1\\ \end{aligned} $$
$$ A'^2=\Big[\frac{\cos^2(ka/2)}{k'}+\frac a2+\frac1{2k}\sin(ka)\Big]^{-1} $$
[複号の下を取れば]
$$\varphi_l(x)=iA'\sin(-ka/2)e^{k'x}$$
$$\varphi_m(x)=iA'\sin\big(k(x-a/2)\big)$$
$$\varphi_r(x)=iA'\sin(ka/2)e^{-k'(x-a)}$$
$$-(k'a/2)\sin(ka/2)=(ka/2)\cos(ka/2)$$
$$ A'^2=\Big[\frac{\sin^2(ka/2)}{k'}+\frac a2-\frac1{2k}\sin(ka)\Big]^{-1} $$
のように、それぞれ $x=a/2$ を中心に $\cos$ 的、$\sin$ 的な波動関数となる。
$k,k'$ についての条件式の両辺を二乗した上で $k'^2+k^2=\frac{2mV}{\hbar^2}$ の関係を使って書き直せば、
[$\cos$ 的な関数について]
$$(ka/2)^2(1+\tan^2(ka/2))=\frac{mVa^2}{2\hbar^2}\ \text{ただし}\ \tan(ka/2)>0$$
[$\sin$ 的な関数について]
$$(ka/2)^2(1+\cot^2(ka/2))=\frac{mVa^2}{2\hbar^2}\ \text{ただし}\ \tan(ka/2)<0$$
を得る。
運動エネルギーとポテンシャルエネルギー †
$\varepsilon\ll V$ を仮定してポテンシャルエネルギーの期待値を求める。
[複号の上を取れば]
$$ A'^2\sim \frac{2}{a} $$
と近似できるから、
$$ \begin{aligned} \langle V\rangle&= \int_{-\infty}^\infty V(x)|\varphi(x)|^2dx =2\int_{-\infty}^0V|\varphi_l(x)|^2dx\\ &=\frac{4V\cos^2(ka/2)}{a}\int_{-\infty}^0e^{2k'x}dx=\frac{2V\cos^2(ka/2)}{k'a}\\ \end{aligned} $$
$\varepsilon\ll V$ のとき $k'\sim\frac{\sqrt{2mV}}\hbar$ であり、
$\frac k{k'}\sim \sqrt{\frac{\varepsilon}{V}}=\frac{\cos(ka/2)}{\sin(ka/2)}\sim \cos(ka/2)$
であるから $V\to\infty$ のとき、
$$ \begin{aligned} \langle V\rangle&\sim \frac{\sqrt2\hbar^2\varepsilon}{\sqrt ma}V^{-3/2}\to0\\ \end{aligned} $$
[複号の下] を取っても同様で、井戸が深い時はポテンシャルエネルギーはゼロとなり、系の持つエネルギーはすべて運動エネルギーと見なせるようになる。
グラフ化 †
- 左図:ポテンシャルと連続的に変化させてグラフを書かせる
- 右図:全エネルギー(実線)に占めるポテンシャルエネルギー(破線)の割合
- 始めは波数ゼロなので運動エネルギーなし、すべてポテンシャル
- 最後は $x^{-3/2}$ で減衰してポテンシャルがゼロになる
LANG:mathematica
calcK[v_, n_] := k /. FindRoot[ (* 挟み撃ちっぽく探す *)
If[Tan[k/2] > 0, (k/2)^2 (1 + Tan[k/2]^2),
(k/2)^2 (1 + Cot[k/2]^2)] - v/2,
{k, (n - 1) Pi + 0.0001, n Pi - 0.01}, Method -> "Brent"]
curve[x_, v_, n_] := Module[{k},
k = calcK[v, n];
If[Mod[n, 2] == 1,
If[x < 0, Cos[-k/2] Exp[Sqrt[2 v - k^2] x],
If[x < 1, Cos[ k(x - 1/2)],
Cos[ k/2] Exp[-Sqrt[2 v - k^2] (x - 1)]]],
If[x < 0, Sin[-k/2] Exp[Sqrt[2 v - k^2] x],
If[x < 1, Sin[ k(x - 1/2)],
Sin[ k/2] Exp[-Sqrt[2 v - k^2] (x - 1)]]]
]]
images = Table[
Module[{k, curves, bases},
curves = {}; bases = {};
For[n = 1, ((n - 1) Pi/2)^2 < v/2, n++,
k = calcK[v, n];
curves = Append[curves, 10 curve[x, v, n] + k^2/2];
bases = Append[bases, k^2/2]
];
Show[
Plot[curves, {x, -0.5, 1.5}, PlotRange -> {0, 220}],
Plot[bases, {x, -0.5, 1.5}, PlotStyle -> {Dashed}],
ListLinePlot[{{-1, v}, {0, v}, {0, 0}, {1, 0}, {1, v}, {2, v}}, PlotStyle -> {{Black, Thick}}]]
], {v, 1, 200, 1}];
Export["finite_well.gif", images]
Module[{n, v, k, energies, energies2, a2, vs},
energies = Table[{}, {n, 1, 7}];
energies2 = Table[{}, {n, 1, 7}];
For[n = 1, n <= 7, n++,
vs = 0.01;
For[v = 2 ((n - 1) Pi/2)^2 + 0.01, v <= 200, v = v + vs,
vs = 1.2 vs;
vs = If[(v < 199) && (v + vs > 200), vs = 199.9 - v, vs];
k = calcK[v, n];
a2 = 1/NIntegrate[curve[x, v, n]^2, {x, -Infinity, Infinity}];
AppendTo[energies[[n]], {v, k^2/2}/2];
AppendTo[energies2[[n]], {v, 2 v NIntegrate[a2 curve[x, v, n]^2, {x, -Infinity, 0}]}/2]
]
];
Show[
ListLinePlot[energies],
ListLinePlot[energies2, PlotStyle -> Dashed],
ListLinePlot[{{0, 0}, {100, 100}}, PlotStyle -> {{Black, Dotted}}]
]
]
時間に依存しないシュレーディンガー方程式の束縛解は実数関数として書き表すことができる †
時間に依存しないシュレーディンガー方程式の複素共役を取れば、
$$\Big(-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}+V(x)\Big)\varphi^*(x)=\varepsilon\varphi^*(x)$$
であるから、$\varphi^*(x)$ も同じ固有値 $\varepsilon$ の固有関数となる。
縮退のない場合*2上で見たように一次元の束縛状態に縮退はおきない、$A$ を定数として $\varphi^*(x)=A\varphi(x)$ と書けることになるが、 固有関数が規格化されているならば $|A|=1$ すなわち $A=e^{i\theta}$ と書ける。
このとき $\varphi^*(x)=e^{i\theta}\varphi(x)$ の両辺を $e^{i\theta/2}$ で割れば、
$$e^{-i\theta/2}\varphi^*(x)=e^{i\theta/2}\varphi(x)$$
$$\Big(e^{i\theta/2}\varphi(x)\Big)^*=e^{i\theta/2}\varphi(x)$$
であるから、
$$\varphi_\mathrm{real}(x)=e^{i\theta/2}\varphi(x)$$
と書けばこれは固有関数であり、なおかつ実数値関数である。
LANG:mathematica
Plot[{x^2,
If[Tan[x] < 0, Infinity, x^2 (1 + Tan[x]^2)],
If[Cot[x] > 0, Infinity, x^2 (1 + Cot[x]^2)]
}, {x, 0, 14}, PlotRange -> {0, 200},
PlotLegends -> Placed[{"連続限界", "cos 的", "sin 的"}, Above],
BaseStyle -> {FontSize -> 18}, ImageSize -> Large,
PlotStyle -> {{Gray, Dashed}, Blue, Purple},
Filling -> {1 -> Axis}, FillingStyle -> {1 -> {Black, Opacity[0.05]}},
AxesLabel -> {ka/2, mVa^2/(2 \[HBar]^2)}
]
NSolve[x^2 (1 + Tan[x]^2) == 50 && Tan[x] > 0 && 0 < x < 10, x, WorkingPrecision -> 15]
(* {{x -> 1.37508316964374}, {x -> 4.09477807780528}, {x -> 6.63585976688118}} *)
NSolve[x^2 (1 + Cot[x]^2) == 50 && Cot[x] < 0 && 0 < x < 10, x, WorkingPrecision -> 15]
(* {{x -> 2.74319088650076}, {x -> 5.41164383515459}} *)
coslike[x_, k_] := Module[{k2 = Sqrt[4 50 - k^2]},
Sign[k] If[x < 0, Cos[k/2] Exp[k2 x],
If[x < 1, Cos[k (x - 1/2)], Cos[k/2] Exp[-k2 (x - 1)]]] 10 + k^2
]
sinlike[x_, k_] := Module[{k2 = Sqrt[4 50 - k^2]},
If[x < 0, -Sin[k/2] Exp[k2 x],
If[x < 1, Sin[k (x - 1/2)], Sin[k/2] Exp[-k2 (x - 1)]]] 10 + k^2
]
Plot[{
coslike[x, 2 1.37508316964374341419334462792217407823`15.],
sinlike[x, -2 2.74319088650075787031867823175879453346`15.],
coslike[x, -2 4.0947780778052791609523226938312581713`15.],
sinlike[x, 2 5.41164383515459114436056269363192749999`15.],
coslike[x, 2 6.63585976688118310914259741089030967404`15.]
},
{x, -0.5, 1.5}, PlotRange -> {0, 300}, ImageSize -> Large,
BaseStyle -> {FontSize -> 20},
Axes -> {True, False},
PlotStyle -> {Thick, Thin, Thin, Thin, Thin, Thin},
AspectRatio -> 1
]
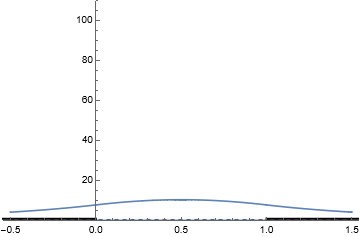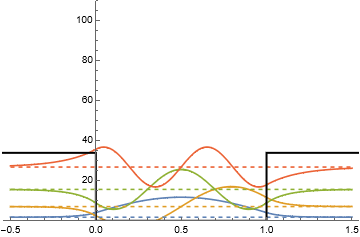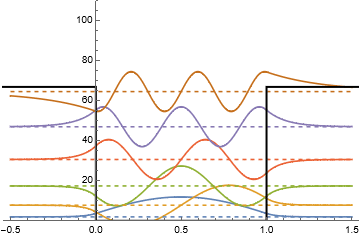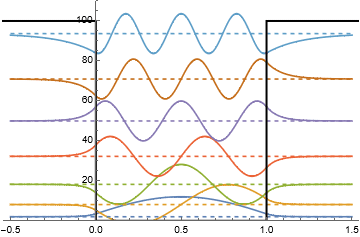
sin[x_, n_] := If[x < 0, 0, If[x > 1, 0, Sin[n Pi x]]] 10 + (n Pi)^2
Plot[{If[x < 0, 500, If[x < 1, 0, 500]],
sin[x, 1], sin[x, 2], sin[x, 3], sin[x, 4], sin[x, 5] },
{x, -0.5, 1.5}, PlotRange -> {0, 300}, ImageSize -> Large,
BaseStyle -> {FontSize -> 20},
Axes -> {True, False},
PlotStyle -> {Thick, Thin, Thin, Thin, Thin, Thin},
AspectRatio -> 1
]
*1 上式の左辺は2次のロンスキー行列式であり、本来はこれがゼロであるかどうかを見るだけで線型独立性の判別ができる(→ Wikipedia:ロンスキー行列式)。以下は初等的に理解するための蛇足。
*2 上で見たように一次元の束縛状態に縮退はおきない