公開メモ
エバース・モルモデル †
主要なパラメータ:
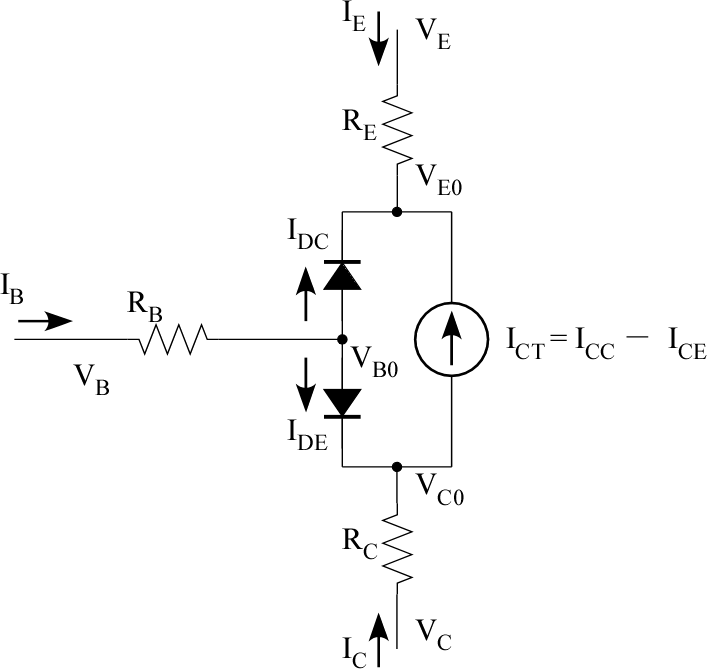
- ベースダイオードの飽和電流
- ベースダイオードの電流立ち上がり特性
- 順方向、逆方向の増幅率
を指定できる。
等が入っていないモデルである。
ガンメルプーン直流モデル †
主要なパラメータ:
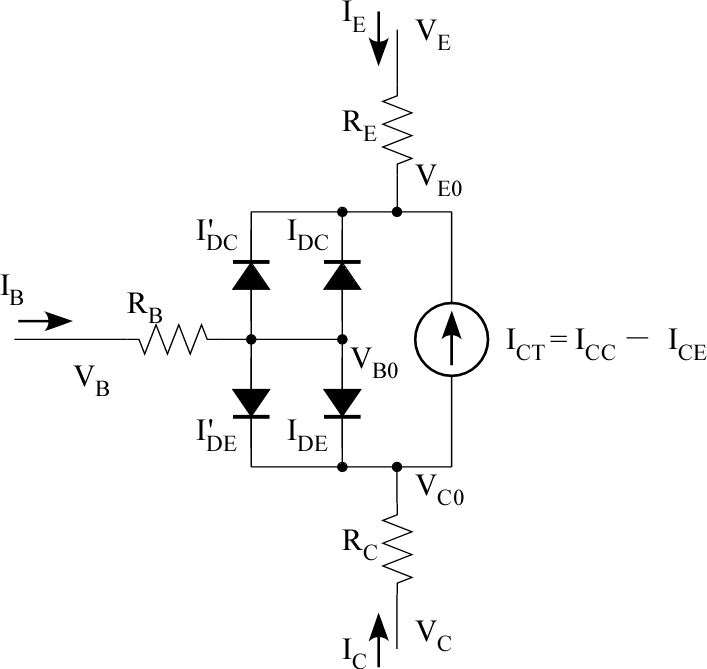
これらは低注入領域での増幅率低下を取り入れるために導入されたダイオード。
こちらのダイオードを通る電流は増幅に寄与しない。
さらに、高注入領域での増幅率低下はベース領域における少数キャリア密度が高すぎるために電流注入効率が減少することにより生じる。ベース領域の電荷密度を熱平衡状態での値で割った値を
とすると、注入効率は
に反比例して減少する。
ここで、
は
に沿って注入されるキャリアの寄与により、
と書ける。1つ目の括弧をアーリー効果と呼び、2つ目の括弧を高注入効果と呼ぶ。
具体的な形は、次のようになる。
-
,
は順方向(F)・逆方向(R)のアーリー(A)電圧(V)
-
,
は順方向(F)・逆方向(R)のニー(K)電流(I)
と呼ばれる。
さらに、このモデルではベース抵抗
の電流依存性が考慮される。
すなわち、高注入領域での値
と低注入領域での値
を用いて、
である。
うーむ †
これらを元にパラメータを決めたくても、
必要なパラメータを必要な精度で決められるような図がデータシートに与えられていないことが多いみたい???
ちょっと頓挫中。

