Mathematica/ミラー光学系のバックアップ(No.9)

更新

バックアップ一覧
差分を表示
現在との差分を表示
ソースを表示
ソフトウェア/Mathematica/ミラー光学系へ行く。
- 1 (2013-12-18 (水) 11:56:58)
- 2 (2013-12-18 (水) 21:33:52)
- 3 (2013-12-19 (木) 01:35:29)
- 4 (2013-12-19 (木) 14:43:03)
- 5 (2013-12-20 (金) 02:11:12)
- 6 (2013-12-20 (金) 12:28:53)
- 7 (2013-12-20 (金) 22:52:21)
- 8 (2013-12-25 (水) 18:37:07)
- 9 (2013-12-26 (木) 14:42:14)
- 10 (2013-12-26 (木) 23:19:30)

公開メモ

概要 †

ミラー光学系の収差を Mathematica を使って計算してみたい。

Mathematica によるプログラミングはあまり慣れていないので、いろいろとまどろっこしいことをしていると思いますが、ご容赦ください。

前提 †

まずは収差のない場合のおさらいから。

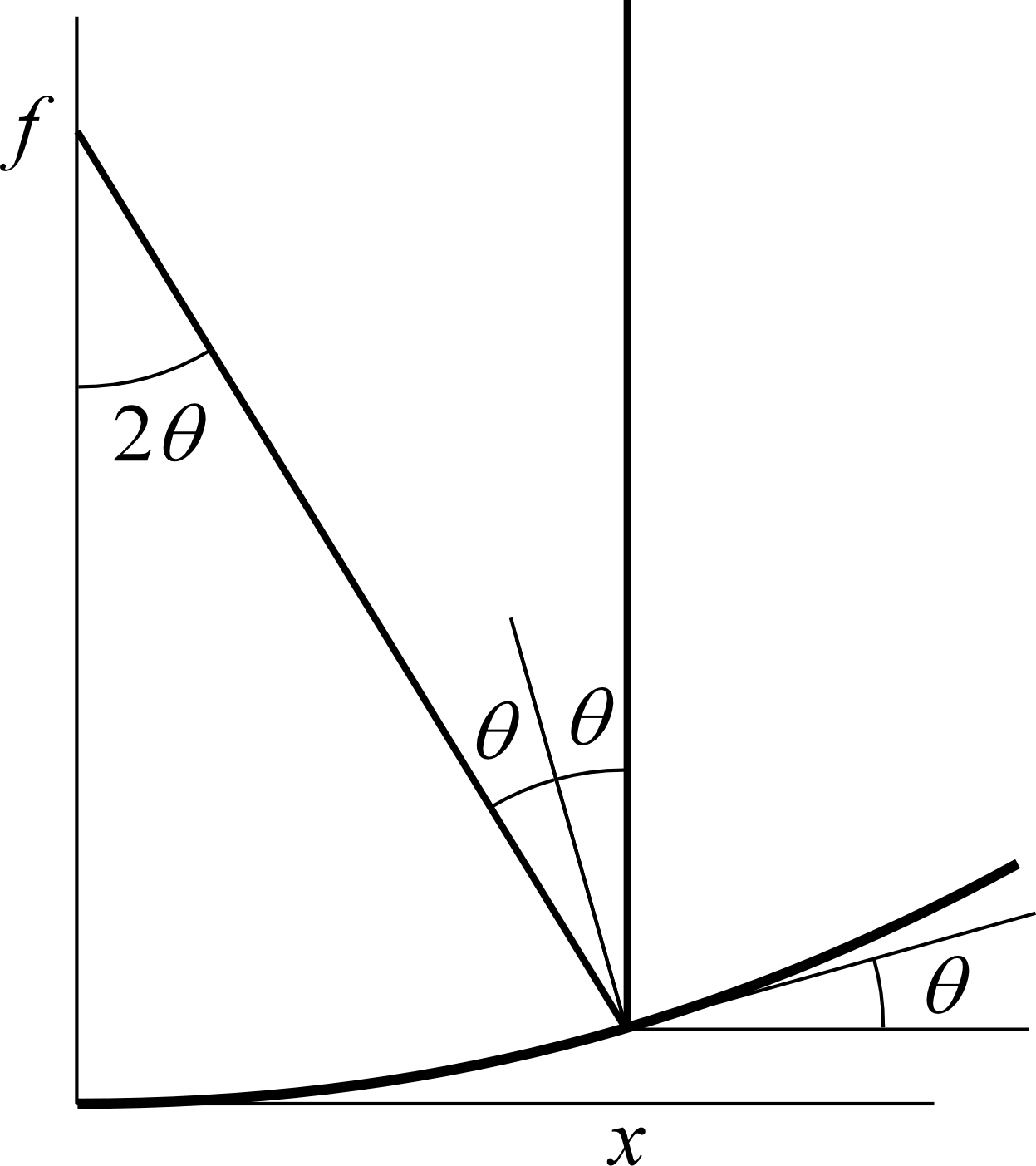
焦点距離と曲率 †

曲率がで表わされる凹面ミラーのの位置に垂直に平行光が入射するとき、

反射面の傾きはなので、小角近似では

入射光はだけ曲がって反射されるので、

すなわち、焦点距離はとなる。

曲率と曲率半径 †

原点を通る半径の円

をについての小さなところで解くと、

したがって、曲率半径に対して、となり、焦点距離は

となる。

点光源からの光を集光する †

凹面鏡の中心軸上、の距離に置かれた点光源から、凹面鏡上のの位置に到達する光が法線からだけずれているとすると、

の関係がなりたつ。平面鏡であればこの光は反射角で反射されるが、凹面鏡の傾きがであれば、実際の反射角はとなる。

このようにして中心軸上に集められる光の焦点位置は、

となるから、

の関係が得られる。

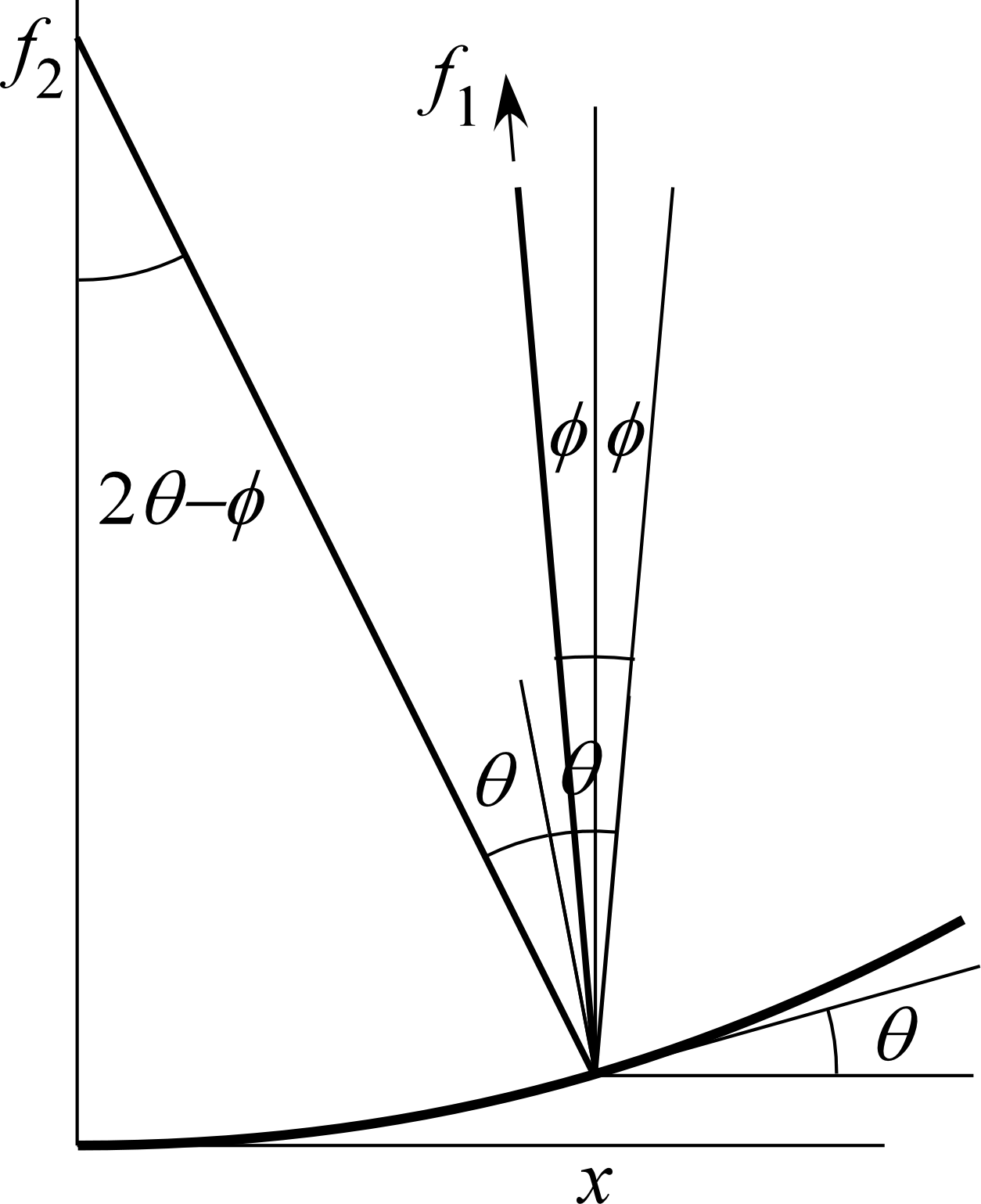
斜め入射の場合 †

中心線に対しての角度で入射する平行光に対する焦点位置を考える。

中心位置で反射される光は反射角で反射される

位置で反射される光は反射角で反射される

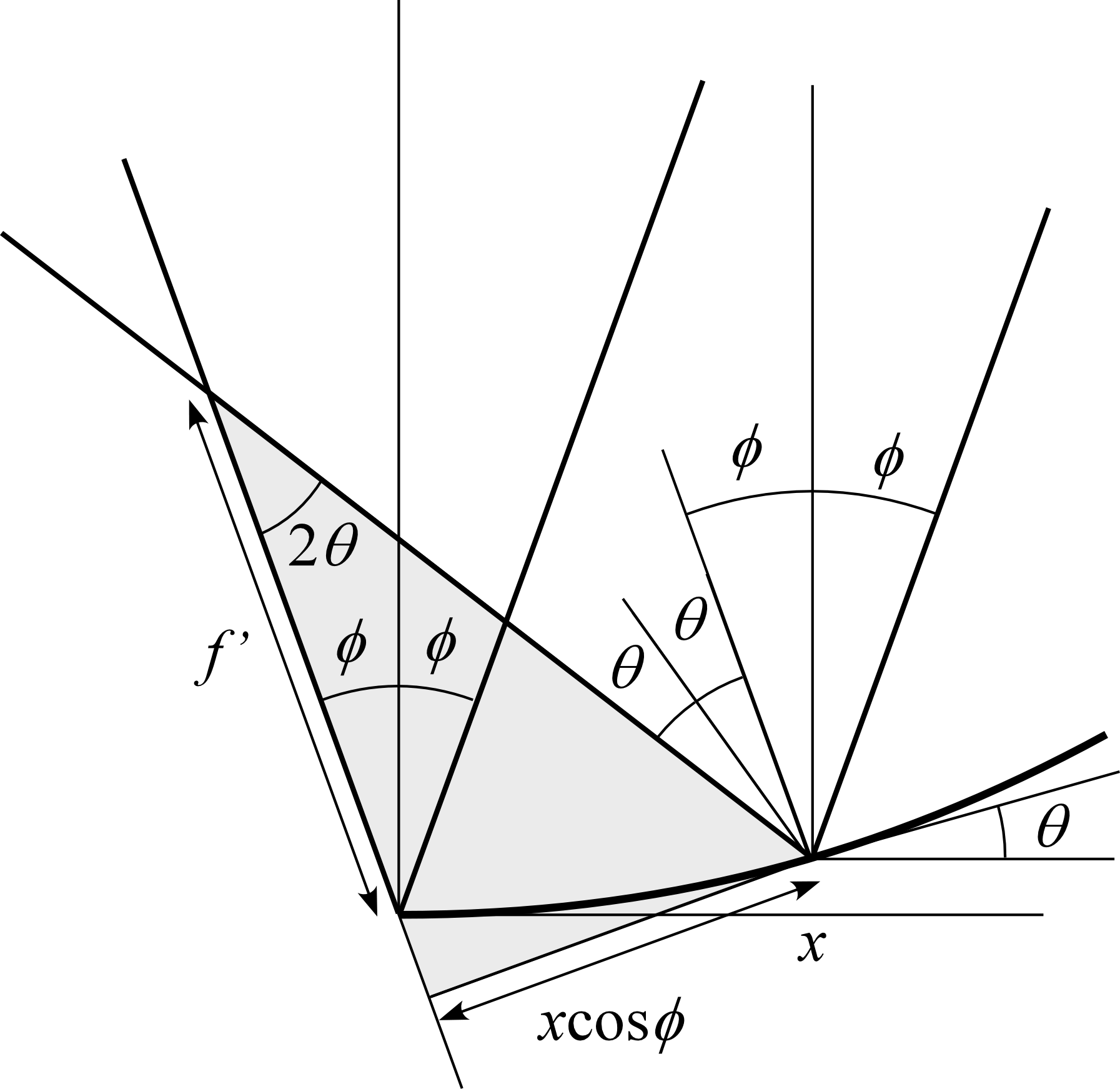
これらの光の為す角はだから、色を付けた三角形を考えることで、

&math( f_\parallel=\frac{x\cos\phi}{2\theta}=\frac{x\cos\phi}{4ax}=\frac{\cos\phi}{4a}=f\cos\phi );

となって、のファクターだけ焦点距離が短くなる。

一方で入射面に垂直な方向には、入射面に垂直な面へ投影した際の焦点距離が元の焦点距離と等しくなることから、斜めに進む分だけ焦点距離が長くなる。

&math( f_\perp=f/\cos\phi );

したがって入射面内での光の収束位置と入射面に垂直な方向への光の収束位置とがずれてしまうことになる。すなわち凹面鏡への斜め入射は大きな収差（非点収差）を生むことになる。

この収差を無くすため、斜め入射で用いるための凹面鏡は入射面内の曲率半径と、垂直方向の曲率半径をだけ違えて設計され、トロイダル凹面鏡などと呼ばれる。

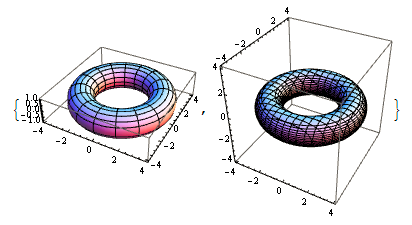
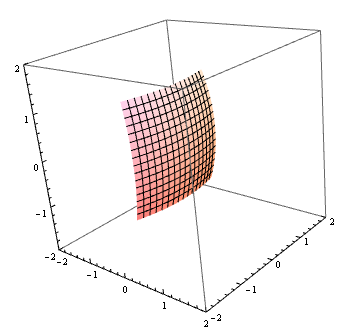
トロイダル凹面鏡の面は数学的にはドーナツ面（トーラス面）の側面として表せる。

数値計算で確かめてみる †

以下は Wolfram Mathematica 9.0 による結果です。

トーラス面 †

まずはトーラス面（ドーナツ面、トロイダル面）を作成してみます。

パラメータ表示

&math( \left\{\begin{array}{l} x=o_x+r_1\cos s+r_2\cos t\cos s\\ y=o_y+r_1\sin s+r_2\cos t\sin s\\ z=o_z+\phantom{r_1\sin s+}\ \,r_2\sin t\\ \end{array}\right . );

と、

方程式表示

(* ドーナツ面のパラメータ表示 *)
(* r1=0 で球面を表わせる *)
torusPar[m_,s_,t_]:=
  Module[{o,r1,r2,ss,tt},
    {o,r1,r2,srange,trange}=m;
    ss = s srange[[1]] + (1-s) srange[[2]];
    tt = t trange[[1]] + (1-t) trange[[2]];
    o + {
      r1 Cos[ss]+r2 Cos[tt] Cos[ss],
      r1 Sin[ss]+r2 Cos[tt] Sin[ss],
      r2 Sin[tt]
    }
  ]

(* ドーナツ面の方程式表示 *)
(* r1=0 で球面を表わせる *)
torusEq[m_] := 
  Module[{o, r1, r2, sr, tr, d}, 
    {o, r1, r2, sr, tr} = m; 
    (Sqrt[(x - o[[1]])^2 + (y - o[[2]])^2] - r1)^2 + (z - o[[3]])^2 == r2^2
  ]

(* 
どちらも引数 m には、

- o: 中心位置
- r1: 半径１ ( = 0 なら球になる)
- r2: 半径２
- sr: パラメータ s の範囲
- tr: パラメータ t の範囲

をリストにした物を与える
*)

試しに表示してみると、

With[ {m = {{0, 0, 0}, 3, 1, {0, 2 Pi}, {0, 2 Pi}}}, {
  ParametricPlot3D[torusPar[m, s, t], {s, 0, 1}, {t, 0, 1}], 
  ContourPlot3D[Evaluate[torusEq[m]], {x, -4, 4}, {y, -4, 4}, {z, -4, 4}]
}]

うまくいっている。

範囲を指定することでミラーの領域を限ることもできる

With[{m = {{-4, 0, 0}, 0, 4, {-Pi/8, Pi/8}, {-Pi/8, Pi/8}}}, 
  ParametricPlot3D[
    torusPar[m, s, t], {s, 0, 1}, {t, 0, 1},
    PlotRange -> {{-2, 2}, {-2, 2}, {-2, 2}}]
  ]

直線 †

次に光線の軌跡を表わすのに用いる直線のパラメータ表示と方程式表示。

方程式表示はちょっと面倒だ。。。

(* 直線のパラメータ表示 *)
linePar[l_, t_] := 
  Module[{p, v},
    {p, v} = l; 
    p + t*v
  ]

(* 直線の方程式表示 *)
lineEq[l_] := Module[{p, v}, 
    {p, v} = l;
    If[v[[1]] == 0, 
      If[v[[2]] == 0, 
        If[v[[3]] == 0, 
          {x, y, z} == p, 
          {x, y} == {p[[1]], p[[2]]}
        ], 
        If[v[[3]] == 0, 
          {x, z} == {p[[1]], p[[3]]}, 
          x == p[[1]] && (y - p[[2]])/v[[2]] == (z - p[[3]])/v[[3]]
        ]
      ], 
      If[v[[2]] == 0, 
        If[v[[3]] == 0, 
          {y, z} == {p[[2]], p[[3]]}, 
          y == p[[2]] && (x - p[[1]])/v[[1]] == (z - p[[3]])/v[[3]]
        ], 
        If[v[[3]] == 0, 
          z == p[[3]] && (x - p[[1]])/v[[1]] == (y - p[[2]])/v[[2]], 
          (x - p[[1]])/v[[1]] == (y - p[[2]])/v[[2]] == (z - p[[3]])/v[[3]]
        ]
      ]
    ]
  ]

(*
  どちらも引数 l には、
  
   - p: 開始位置
   - v: 方向ベクトル

 をリストにした物を与える
*)

トーラス面と直線との交点・反射光 †

上記のトーラス面と直線を使って計算していく。

(* 直線とトーラス面との交点を求めてトーラス面のパラメータで返す *)
intersection[l_, m_] := 
  Module[{points, params, o, r1, r2, srange, trange, delta}, 
    delta = 10^(-5);
    {o, r1, r2, srange, trange} = m; 
    (* 交点を求め *)
    points = NSolve[torusEq[m] && lineEq[l], {x, y, z}];
    (* パラメータ表示に直す *)
    params = Map[
      Function[ point, 
        Minimize[{
            Norm[torusPar[m, s, t] - {x, y, z}] /. point (*, 
            0-delta < s < 1+delta && 0-delta < t < 1+delta*)
          }, {s, t}
        ][[2]]
      ], points];
    (* 範囲外の物を除く *)
    Select[ params, 
      0 <= s < 1 && 0 <= t < 1 /. #1 & ]
  ]

(* トーラス面上の s, t で表わされる点における法線ベクトルを求める *)
normalVector[m_, s_, t_] := 
  Normalize[
    Cross[ 
      D[torusPar[m, ss, tt], ss], 
      D[torusPar[m, ss, tt], tt]
    ] /. {ss -> s, tt -> t}
  ]

(* 入射方向ベクトルと法線ベクトルから反射方向ベクトルを求める *)
reflection[v_, n_] := 
  Module[ { 
      vv = Normalize[v], 
      nn = Normalize[If[v . n < 0, -n, n]]
    }, Normalize[vv - 2*vv . nn*nn] ]

(* 直線 l がトーラス面 m で反射する様子を追跡する *)
(* 反射点と反射方向ベクトルを返す *)
trace[l_, m_] := 
  Module[{p, v, st, q, n, r}, 
    {p, v} = l; 
    list = intersection[l, m]; 
    Map[ 
      Function[ st,
        q = torusPar[m, s, t] /. st; 
        n = normalVector[m, s, t] /. st; 
        r = reflection[v, n]; 
        {q, r}
      ], list
    ]
  ]

入射光の分布を作りグラフ表示 †

(* ベクトル v を v x z 方向に a, v x (v x z) 方向に b ずらす *)
offsetVector[v_, a_, b_] := 
  Module[{ez = {0, 0, 1}, ea, eb}, 
    ea = Normalize[Cross[v, ez]]; 
    eb = Normalize[Cross[v, ea]]; 
    v + a*ea + b*eb
  ]

(* 点 a と点 b を結ぶ線分を表示する *) 
showSegment[a_, b_] := 
 ParametricPlot3D[ t * a + (1 - t) * b, {t, 0, 1}]

を用意しておく。

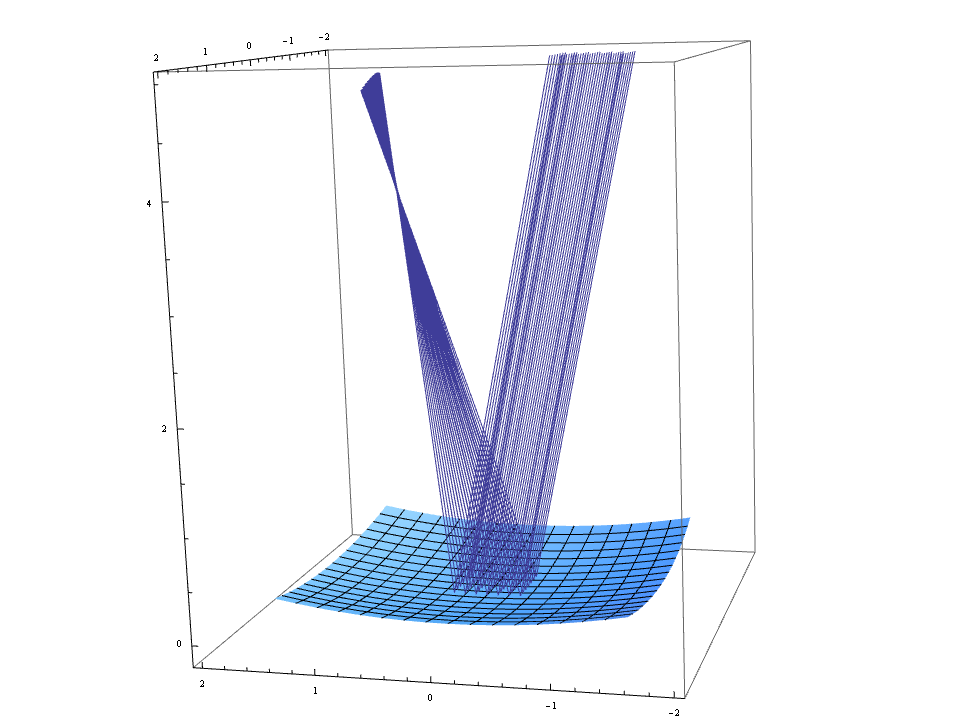
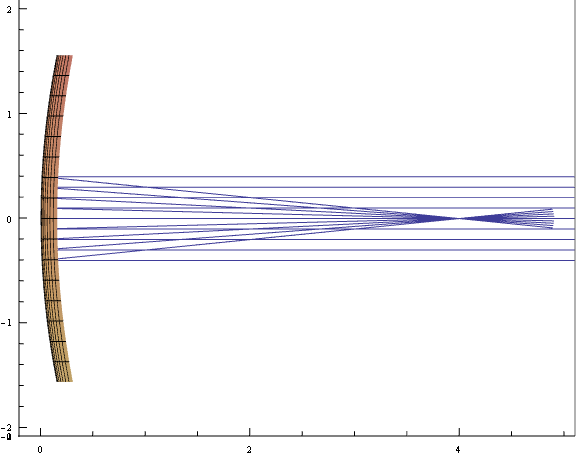
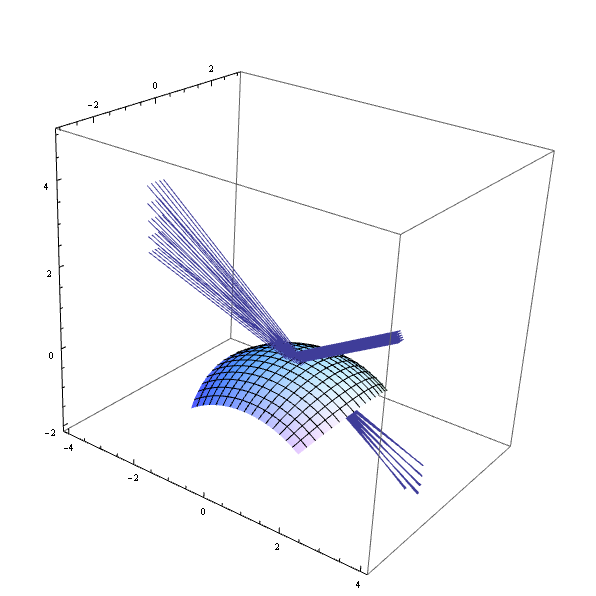
平行光線を球面に斜め入射した際の反射 †

With[{
    n = 3,
    d = 0.1,
    m1 = {{8, 0, 0}, 0, 8, {-Pi/16, Pi/16}, {Pi(1-1/16), Pi(1+1/16)}}
  },
  Show[
    (* ミラーを表示 *)
    ParametricPlot3D[torusPar[m1, s, t], {s, 0, 1}, {t, 0, 1}], 
    (* 複数の光線に対して計算する *)
    Function[ij, 
      Module[{i, j, p, v, q, r, qrs},
        {i, j} = ij;
        p = offsetVector[{10, -2, 0}, i d, j d]; (* 入射光の出発位置     *)
        v = Normalize[{-10, 2, 0}];              (* 入射光の方向ベクトル *)
        Map[
          Function[qr,
            Module[{q, r},
              {q, r} = qr;
              {showSegment[p, q], showSegment[q, q + 5*r]}
            ]
          ],
          trace[{p, v}, m1]                      (* 複数回反射する可能性がある？ *)
        ]
      ]
    ] /@ Flatten[
      Array[
        {#1 - n - 1, #2 - n - 1} &, 
        {2 n + 1, 2 n + 1}
      ], 1
    ],
    PlotRange -> {{-10, 10}, {-2, 2}, {-2, 2}}
  ]
]

半径 8 の球面の焦点距離が予想通り 4 程度になっているのが見て取れる。

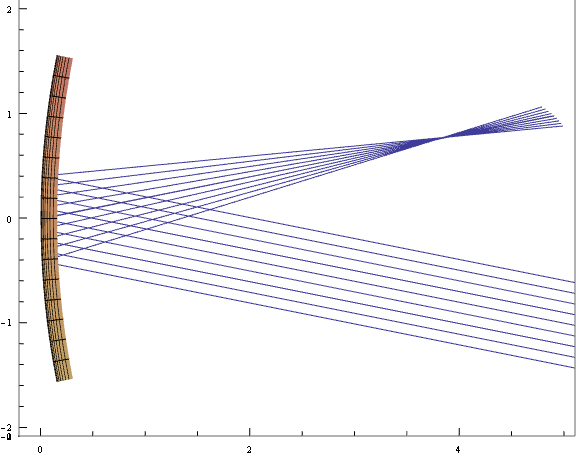
この時の様子を入射面方向と入射面に垂直方向とで比べると、入射面に平行に見た焦点距離が計算通り 4 なのに対して、入射面に垂直に見た焦点距離が明らかに 4 より短いことも分かる。

光線に垂直な面内での光強度分布 †

(* 与えられた直線に直交する平面をパラメータ表示 *)
(* 平面は直線 l 上の位置 d において交わる *)
(* パラメータ s, t の基準となる方向を a で与える *)
perpendicularPlanePar[l_, d_, a_, s_, t_] :=
   Module[{p, v, ea, eb},
      {p,v} = l;
      eb = Normalize[Cross[v, a]];
      ea = Normalize[Cross[eb, v]];
      p + d v + s ea + t eb
  ]

(* 与えられた直線 l0 に直交する平面と、別の直線 l との交点を求める *)
(* 交点は平面のパラメータで表わされる *)
planeSection[l0_, d_, a_, l_] :=
  Module[{p, v, stuList},
    stu = NSolve[
      perpendicularPlanePar[l0, d, a, s, t] == linePar[l, u],
      {s, t, u}
    ];
    {s, t} /. stu
  ]

を用意して、後のために反射光線の束を求めておく

lines = Module[{
    n = 4,
    d = 0.1,
    m1 = {{8, 0, 0}, 0, 8, {-Pi/16, Pi/16}, {Pi(1-1/16), Pi(1+1/16)}},
    indice
  },
  indice = DeleteDuplicates[ Flatten[
      Array[
        {(#1 - n - 1), (#2 - n - 1)} &, 
        {2 n + 1, 2 n+1}
      ], 1     (* 中心線が indice[[0]] に来るようにソートしておく *)
    ]] // Sort[#, (Function[{a,b}, Norm[a]<Norm[b] ]) ] &;
  Map[
    Function[ij, 
      Module[{i, j, p, v, q, r, qrs},
        {i, j} = ij;
        p = offsetVector[{10, -2, 0}, i d, j d];
        v = Normalize[{-10, 2, 0}];
        trace[{p, v}, m1]
      ]
    ], 
    indice
  ] // Flatten[#, 1]&
]

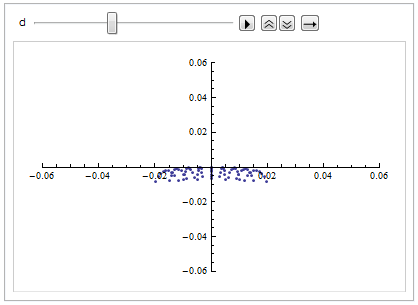
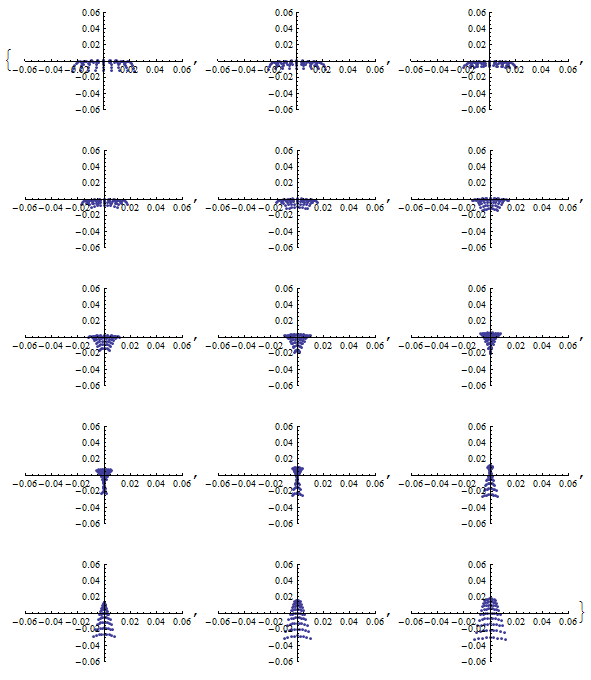
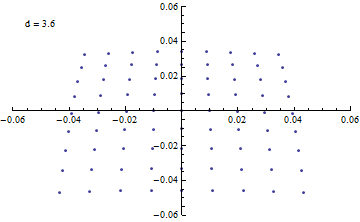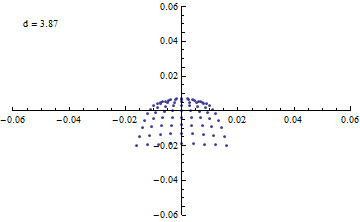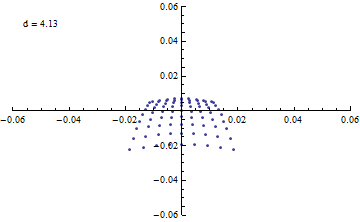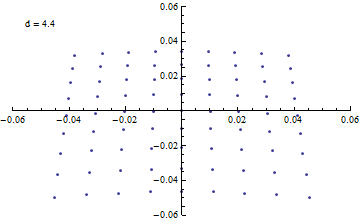
焦点付近でミラーからの距離を変えながら光路に直交する平面との交点をプロットする。

Animate[
  ListPlot[ 
    Map[
       Function[line,
         planeSection[lines[[1]], d, {0,0,1}, line]
       ],
       lines
     ] // Flatten[#, 1] &,
    PlotRange->{{-0.06,0.06},{-0.06,0.06}}
  ],
  {d,3.6,4.4}
]

アニメーションにすると変化が分かりやすい。

SetDirectory["C:\\Users\\osamu\\Desktop"]

Table[
  ListPlot[ 
    Map[
       Function[line,
         planeSection[lines[[1]], d, {0,0,1}, line]
       ],
       lines
     ] // Flatten[#, 1] &,
    PlotRange->{{-0.06,0.06},{-0.06,0.06}}
  ],
  {d,3.6,4.4,0.01}
] // 
Export["reflection.gif", #, "GIF"] &

アニメーションを Web に載せるには、このようにして動画 gif を作ればいい。

Table[
  ListPlot[ 
    Map[
       Function[line,
         planeSection[lines[[1]], d, {0,0,1}, line]
       ],
       lines
     ] // Flatten[#, 1] &,
    PlotRange->{{-0.06,0.06},{-0.06,0.06}}
  ],
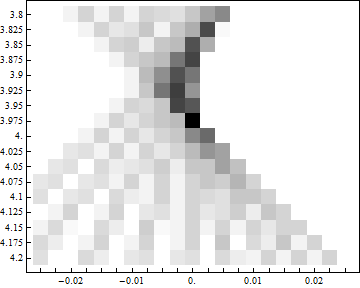
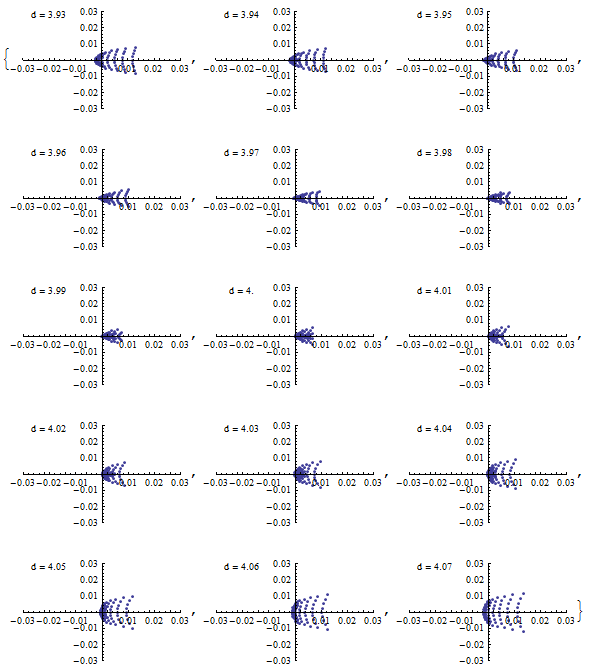
  {d,3.87,4.15,0.02}
]

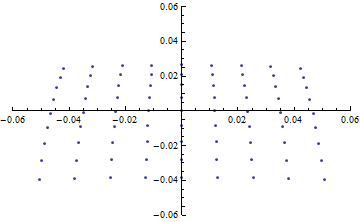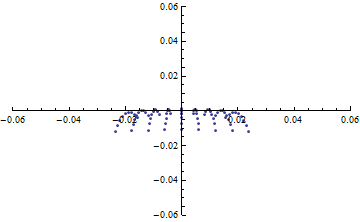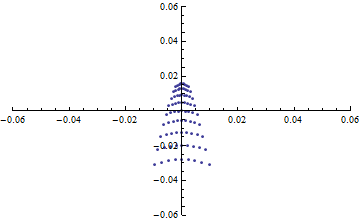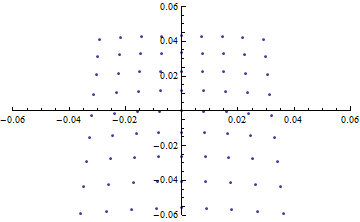
縦と横の焦点距離が違うことが明らかに分かるのと同時に、縦も横も、球面収差などのせいで完璧な直線には収束しないことが分かる。

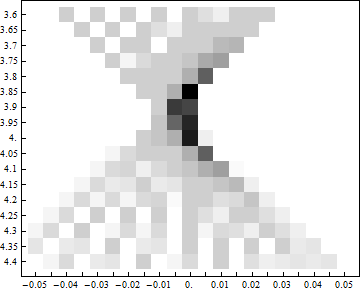
Table[
  HistogramList[
    Map[
      Function[line,
        planeSection[lines[[1]], d, {0,0,1}, line][[1]][[1]]
      ],
      lines
    ],
    {-0.0525,0.0525,0.005}
  ][[2]],
  {d,3.6,4.4,0.05}
] //
ArrayPlot[#, FrameTicks -> {
  Transpose[{Range@17, Table[x, {x, 3.6, 4.4, 0.05}]}], 
  Transpose[{Range@21, 
    Table[If[Abs[Round[100 x] - 100 x] < 0.001, x, ""], {x, -0.05, 0.05, 0.005}]}]
}] &

Table[
  HistogramList[
    Map[
      Function[line,
        planeSection[lines[[1]], d, {0,0,1}, line][[1]][[2]]
      ],
      lines
    ],
    {-0.0525,0.0525,0.005}
  ][[2]],
  {d,3.6,4.4,0.05}
] //
ArrayPlot[#, FrameTicks -> {
  Transpose[{Range@17, Table[x, {x, 3.6, 4.4, 0.05}]}], 
  Transpose[{Range@21, 
    Table[If[Abs[Round[100 x] - 100 x] < 0.001, x, ""], {x, -0.05, 0.05, 0.005}]}]
}] &

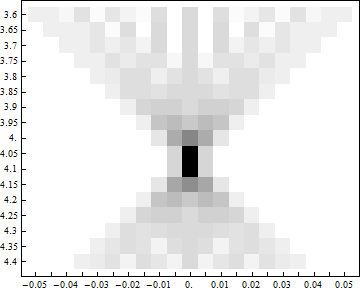
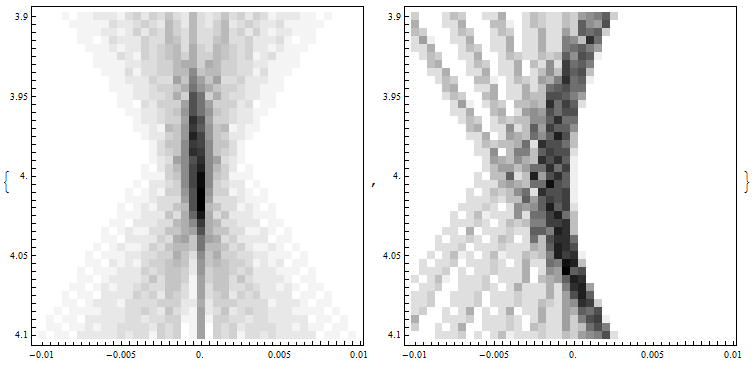
などとして、ミラーからの距離に対する縦方向の幅、横方向の幅をプロットしてみると、各方向に対する焦点距離を比較的正確に見ることができる。

それぞれ、およそ (4 ± 0.075) 程度と見積もれる。

元々の入射角がだから、であり、

見積り通りと言える。

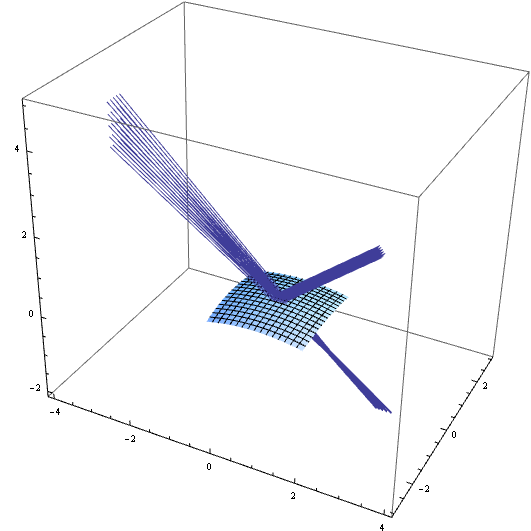
トロイダルミラーによる反射 †

ミラー形状をトラス面にすることで非点収差を補正してみる。

つもりが、、、試したら intersection がうまく動かない場合があったので、まずはそちらを書き換えた。

(* 直線とトーラス面との交点を求めてトーラス面のパラメータで返す *)
intersection[l_, m_] := 
  Module[{d, p}, 
    (* 交点を求める *)
    {d, p} =
      NMinimize[{
          Norm[torusPar[m, s, t] - linePar[l, u]], 
          0 <= s < 1 && 0 <= t < 1
        }, {s, t, u}
      ];
    If[d < 10^-5, {p}, {}]
  ]

気を取り直して、

lines = Module[{
    n = 4,
    d = 0.1,
    f = 4,
    CosPhi = Cos[Tan[2/10]],
    r1, r2, m1,
    indice
  },
  (* 斜め入射により焦点距離が伸びたり縮んだりする分を、曲率を変えて補正する *)
  r1 = 2 f CosPhi   // N;
  r2 = 2 f / CosPhi // N;
  m1 = {{r2, 0, 0}, r2-r1, r1, 
         {Pi-Pi/16, Pi+Pi/16}, {-Pi/16, Pi/16}};
  indice = DeleteDuplicates[ Flatten[
      Array[
       {(#1 - n - 1), (#2 - n - 1)} &, 
        {2 n + 1, 2 n+1}
      ], 1
    ]];
  Map[
    Function[ij, 
      Module[{i, j, p, v},
        {i, j} = ij;
        p = offsetVector[{10, -2, 0}, i d, j d];
         v = Normalize[{-10, 2, 0}];
        trace[{p, v}, m1]
     ]
    ], 
    Sort[indice, Norm[#1]<Norm[#2]&]
  ] // Flatten[#, 1]&
];
 
Animate[
  Show[
    ListPlot[ 
      Map[
         Function[line,
           planeSection[lines[[1]], d, {0,0,1}, line]
         ],
         lines
       ] // Flatten[#, 1] &,
      PlotRange->{{-0.06,0.06},{-0.06,0.06}}
     ],
   Graphics[{Text["d = "<>ToString[d],{-0.05,0.05}]}]
  ],
  {d,3.6,4.4}
]

Table[
  Show[
    ListPlot[ 
      Map[
         Function[line,
           planeSection[lines[[1]], d, {0,0,1}, line]
         ],
         lines
       ] // Flatten[#, 1] &,
      PlotRange->{{-0.06,0.06},{-0.06,0.06}}
    ],
    Graphics[{Text["d = "<>ToString[d],{-0.05,0.05}]}]
  ],
  {d,3.6,4.4,0.01}
] //
Export["13.gif", #, "GIF"] &

Table[
  Show[
    ListPlot[ 
      Map[
         Function[line,
           planeSection[lines[[1]], d, {0,0,1}, line]
         ],
         lines
       ] // Flatten[#, 1] &,
      PlotRange->{{-0.03,0.03},{-0.03,0.03}}
    ],
    Graphics[{Text["d = "<>ToString[d],{-0.02,0.028}]}]
  ],
  {d,3.93,4.07,0.01}
]

Table[
  Table[
    HistogramList[
      Map[
        Function[line,
          planeSection[lines[[1]], d, {0,0,1}, line][[1]][[n]]
        ],
        lines
      ],
      {-0.016,0.0161,0.0008}
    ][[2]],
    {d,3.9,4.101,0.005}
  ] //
  ArrayPlot[#, {FrameTicks -> {
    Transpose[{Range@41, 
      Table[If[Abs[Round[20 x] - 20 x] < 0.001, x, ""], {x, 3.9,4.101,0.005}]}], 
    Transpose[{Range@41, 
      Table[If[Abs[Round[200 x] - 200 x] < 0.001, x, ""], {x, -0.010,0.0101,0.0005}]}]
    },
    ImageSize->Medium}
  ] &, 
  {n,1,2}
]

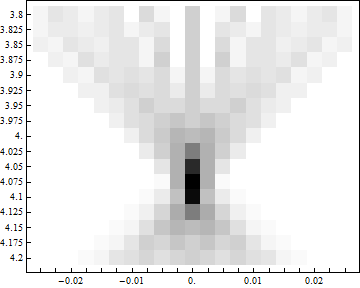
焦点距離はほぼ計算通りが得られているものの、対称性が悪いようで、非等方的な分布になっている。

現実的なミラー †

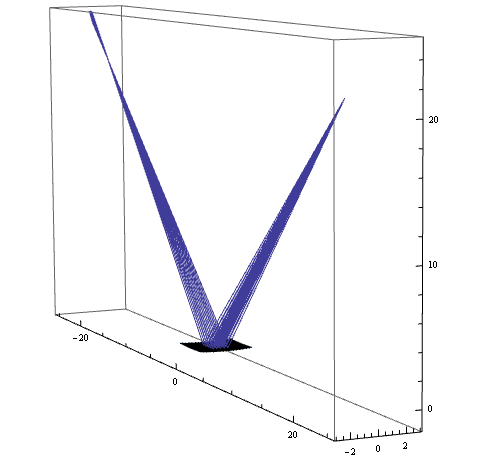
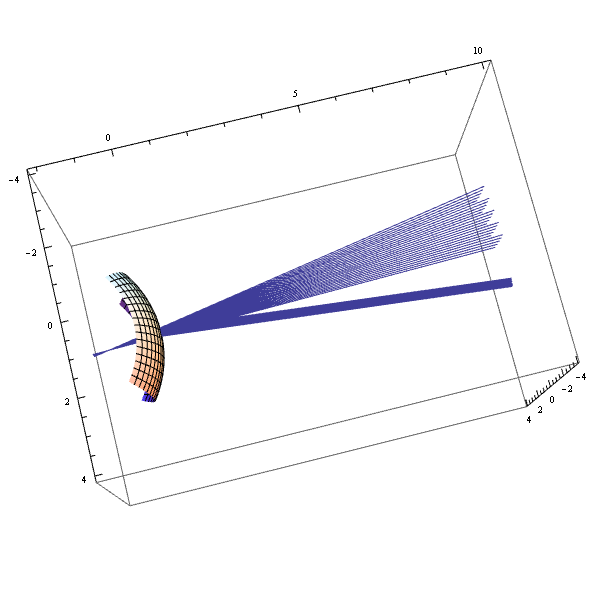
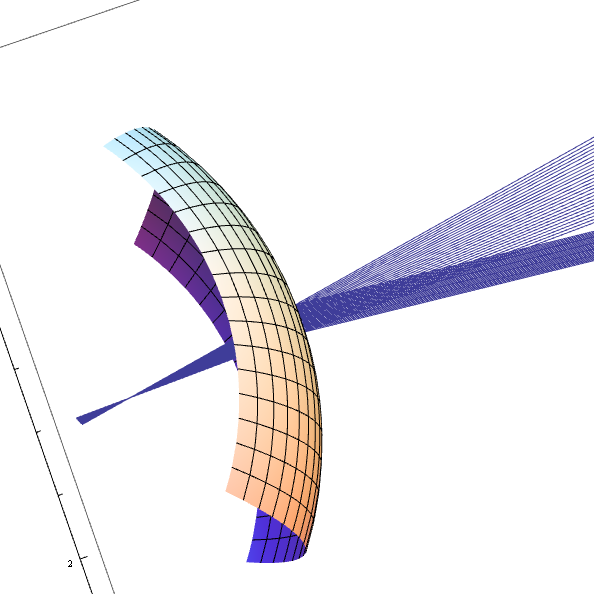
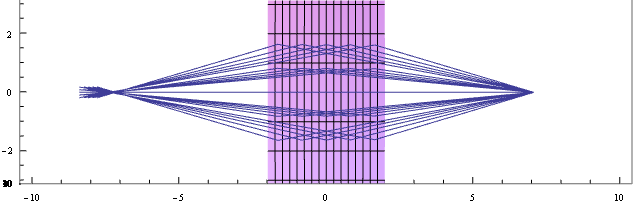
30 cm の距離にある点光源から出た光を 45°入射で反射して、 30 cm の距離に集光するトロイダルミラーを考える。

以下では長さの単位はすべて cm

平行光に対する焦点距離は

45°だと

Module[{
    n = 2,
    d = 0.01,
    f = 15,
    CosPhi = Cos[Pi/4],
    r1, r2, m1
  },
  r1 = 2 f CosPhi   // N;
  r2 = 2 f / CosPhi // N;
  m1 = {{r2, 0, 0}, r2-r1, r1, 
        {Pi-Pi/64, Pi+Pi/64}, {-Pi/64*2, Pi/64*2}};
  Show[
    (* ミラーを表示 *)
    ParametricPlot3D[torusPar[m1, s, t], {s, 0, 1}, {t, 0, 1}], 
    (* 複数の光線に対して計算する *)
    Table[
      Module[{p, v, q, r, qrs},
        p = {30/Sqrt[2], 30/Sqrt[2], 0};                    (* 入射光の出発位置     *)
        v = offsetVector[Normalize[{-1, -1, 0}], i d, j d]; (* 入射光の方向ベクトル *)
        qr = trace[{p, v}, m1];
        If[ Length[qr] > 0,
          {q, r} = qr[[1]];
          {showSegment[p, q], showSegment[q, q + 35*r]},
          {showSegment[p, p+40 v]}]
      ],
      {i, -n, n},
      {j, -n, n}
    ],
    PlotRange -> {{-1, 25}, {-25, 25}, {-3, 3}}
  ]
]

lines = Module[{
    n = 2,
    d = 0.01,
    f = 15,
    CosPhi = Cos[Pi/4],
    r1, r2, m1
  },
  r1 = 2 f CosPhi   // N;
  r2 = 2 f / CosPhi // N;
  m1 = {{r2, 0, 0}, r2-r1, r1, 
        {Pi-Pi/64, Pi+Pi/64}, {-Pi/64*2, Pi/64*2}};
  indice = DeleteDuplicates[ Table[
        {i, j}, {i, -n, n}, {j, -n, n}
    ] // Flatten[#, 1]& ] // Sort[#, Function[{a,b}, Norm[a]<Norm[b]] ] &;
  Map[
    Function[ij, 
      Module[{i, j, p, v},
        {i, j} = ij;
        p = {30/Sqrt[2], 30/Sqrt[2], 0};                    (* 入射光の出発位置     *)
        v = offsetVector[Normalize[{-1, -1, 0}], i d, j d]; (* 入射光の方向ベクトル *)
        trace[{p, v}, m1]
      ]
    ], 
    indice
  ] // Flatten[#, 1]&
];

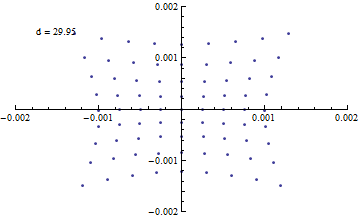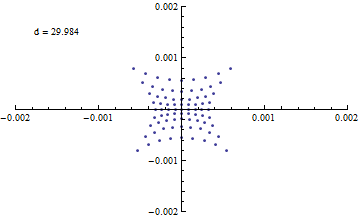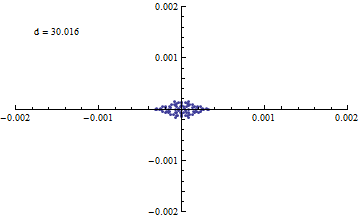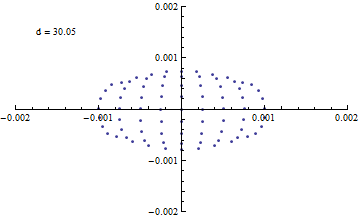
Animate[
  Show[
    ListPlot[ 
      Map[
         Function[ line,
           planeSection[lines[[1]], d, {0,0,1}, line]
         ],
         lines
       ] // Flatten[#, 1] &,
      PlotRange->{{-0.002,0.002},{-0.002,0.002}}
    ],
    Graphics[{Text["d = "<>ToString[d],{-0.0015,0.0015}, Alignment->Left]}]
  ],
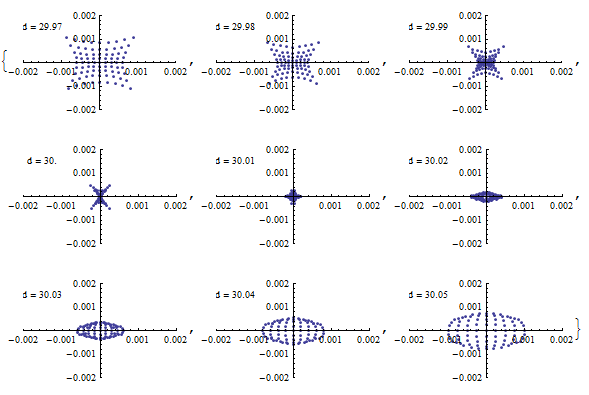
  {d,29.95,30.05}
]

Table[
  Show[
    ListPlot[ 
      Map[
         Function[line,
           planeSection[lines[[1]], d, {0,0,1}, line]
         ],
         lines
       ] // Flatten[#, 1] &,
      PlotRange->{{-0.002,0.002},{-0.002,0.002}}
    ],
    Graphics[{Text["d = "<>ToString[d],{-0.0015,0.0015}, Alignment->Left]}]
  ],
  {d,29.95,30.05,0.002}
] //
Export["17.gif", #, "GIF"] &

Table[
  Show[
    ListPlot[ 
      Map[
         Function[line,
           planeSection[lines[[1]], d, {0,0,1}, line]
         ],
         lines
       ] // Flatten[#, 1] &,
       PlotRange->{{-0.002,0.002},{-0.002,0.002}}
     ],
     Graphics[{Text["d = "<>ToString[d],{-0.0015,0.0015}, Alignment->Left]}]
  ],
  {d,29.97,30.05,0.01}
]

数ミクロン程度まで絞れているように見える。

また、入射・反射の対称性がよいからか、スポット形状もかなり等方的に見える。

凸ミラー †

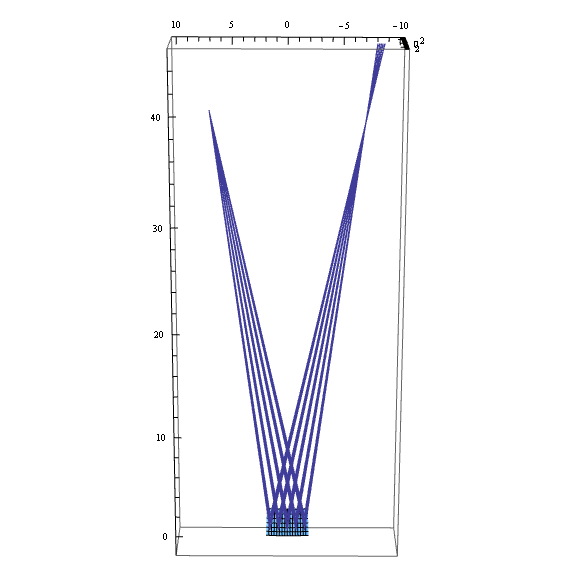
実際には点光源ではなく、平行光を凸ミラーで広げて用いたい。

凸ミラーにもトロイダルな物を使えば最良の結果が得られるはずだけれど、トロイダル凸ミラーは入手性が非常に悪そう。

で、球面凸ミラーを使った場合を考えた。

例えば、1.5 mm 径のレーザービームを 300 mm で 20 倍の 30 mm まで広げたければ、焦点距離がおよそ 300 / 20 = 15 mm の凸ミラーを使えば良い。

Module[{
    n = 2,
    d = 0.05,
    f = 3.102/2 ,
    m1
  },
   m1 = {{-2 f, 0, 0}, 0, 2 f, 
        {Pi-Pi/4*0.8, Pi+Pi/4*0.8}, {Pi-Pi/4*0.8, Pi+Pi/4*0.8}};
  Show[
    ParametricPlot3D[torusPar[m1, s, t], {s, 0, 1}, {t, 0, 1}], 
    Function[ij, 
      Module[{i, j, p, v, q, r, qrs},
        {i, j} = ij;
       p = offsetVector[{10, 1, 0}, i d, j d];
        v = Normalize[{-10, -1, 0}];
        Map[
          Function[qr,
            Module[{q, r},
              {q, r} = qr;
              {showSegment[p, q], showSegment[q - 2 r, q + 10 r]}
            ]
          ],
          trace[{p, v}, m1]
        ]
      ]
    ] /@ Flatten[
      Array[
        {#1 - n - 1, #2 - n - 1} &, 
        {2 n + 1, 2 n + 1}
      ], 1
    ],
    PlotRange -> {{-2, 10}, {-4, 4}, {-4, 4}}
  ]
]

反射光を反対側に集めた先の焦点位置の光の像が凹面鏡で集光された先に形成されることになる。

この部分の分布を見ると、

lines = Module[{
    n = 4,
    d = 0.005,
    f = 3.102/2 ,
    m1
  },
  m1 = {{-2 f, 0, 0}, 0, 2 f, 
        {Pi-Pi/4*0.8, Pi+Pi/4*0.8}, {Pi-Pi/4*0.8, Pi+Pi/4*0.8}};
  indice = DeleteDuplicates[ Table[
        {i, j}, {i, -n, n}, {j, -n, n}
    ] // Flatten[#, 1]& ] // Sort[#, Function[{a,b}, Norm[a]<Norm[b]] ] &;
  Map[
    Function[ij, 
      Module[{i, j, p, v},
        {i, j} = ij;
        p = offsetVector[{10, 1, 0}, i d, j d];
        v = Normalize[{-10, -1, 0}];
        trace[{p, v}, m1]
      ]
    ], 
    indice
  ] // Flatten[#, 1]&
];

Animate[
  Show[
    ListPlot[ 
      Map[
         Function[ line,
           planeSection[lines[[1]], d, {0,0,1}, line]
         ],
         lines
      ] // Flatten[#, 1] &,
      PlotRange->{{-0.001,0.001},{-0.001,0.001}}
    ],
   Graphics[{Text["d = "<>ToString[d],{-0.00075,0.00075}, Alignment->Left]}]
  ],
  {d,-1.5,-1.6}
]

Table[
  Show[
    ListPlot[ 
      Map[
         Function[ line,
           planeSection[lines[[1]], d, {0,0,1}, line]
         ],
         lines
      ] // Flatten[#, 1] &,
      PlotRange->{{-0.001,0.001},{-0.001,0.001}}
    ],
    Graphics[{Text["d = "<>ToString[d],{-0.00075,0.00075}, Alignment->Left]}]
  ],
  {d,-1.5,-1.6,-0.002}
] //
Export["reflection.gif", #, "GIF"] &

当然ではあるが、縦と横とで焦点距離が異なってしまっている。

とはいえ引き延ばされたスポット径はかなり小さくて、それほどひどいことにはなっていない。

Table[
  Show[
    ListPlot[ 
      Map[
         Function[line,
           planeSection[lines[[1]], d, {0,0,1}, line]
         ],
         lines
       ] // Flatten[#, 1] &,
       PlotRange->{{-0.002,0.002},{-0.002,0.002}}
     ],
     Graphics[{Text["d = "<>ToString[d],{-0.0015,0.0015}, Alignment->Left]}]
  ],
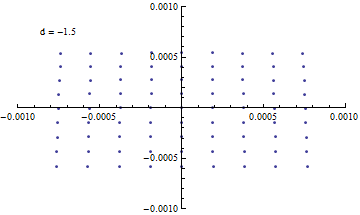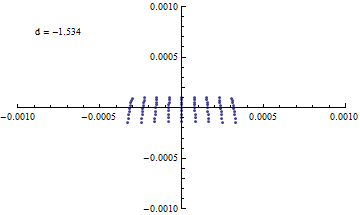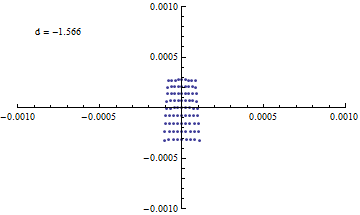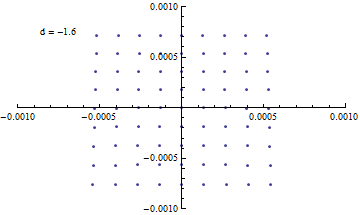
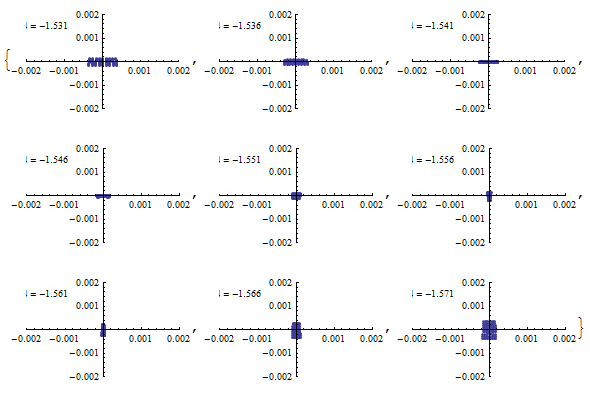
  {d,-1.531,-1.571,-0.005}
]

これを見る限り、何も考えずに組み合わせても数ミクロンまで絞れそう。

さらに、凹面ミラーを少しだけ傾けて使うことで、凸ミラーでの非点収差を打ち消せるはずなので、実際にはこれよりさらに良い結果を期待できる。

球面ミラー２枚で使えないか？ †

凹面ミラーの非点収差 †

トロイダルミラーは高価なので、球面凸ミラーと球面凹ミラーを組み合わせて非点収差を打ち消せないか考えてみる。

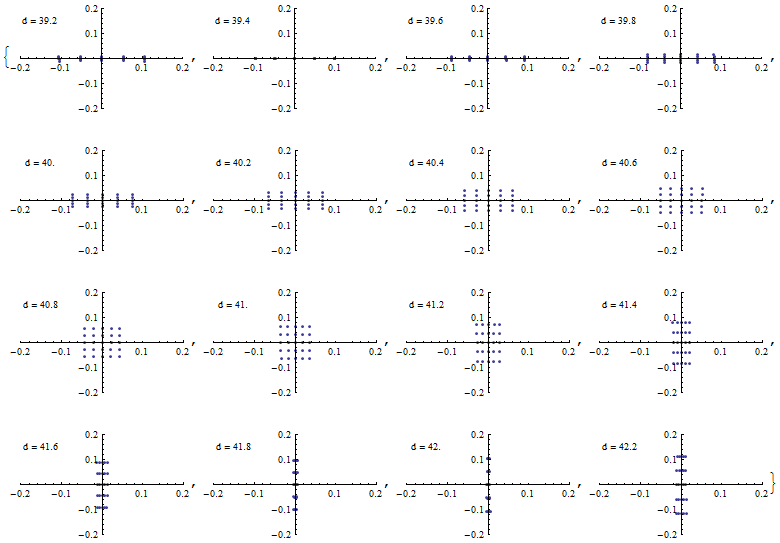
例えば焦点距離 203.20 mm の凹面ミラーを両側 406.4 mm の焦点距離で使うとする。

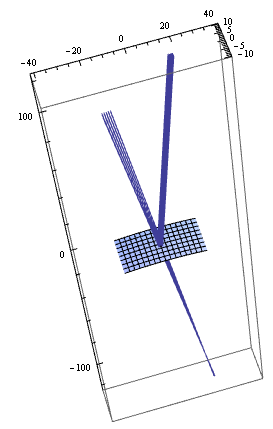
ミラー上でのビーム径を 30 mm 程度とすると、広がり角は 4.2°程度しかないため、例えば入射角 10°程度でも使えないことはない？

Module[{
    n = 2,
    d = 0.02,
    f = 20.320,
    theta = 10 Pi/180,
    m1
  },
  m1 = {{2 f, 0, 0}, 0, 2 f, 
        {Pi-Pi/64, Pi+Pi/64}, {-Pi/64*4, Pi/64*4}};
  Show[
    (* ミラーを表示 *)
    ParametricPlot3D[torusPar[m1, s, t], {s, 0, 1}, {t, 0, 1}], 
    (* 複数の光線に対して計算する *)
    Table[
      Module[{p, v, q, r, qrs},
        p = {2 f Cos[theta], 2 f Sin[theta], 0};                              (* 入射光の出発位置     *)
        v = offsetVector[Normalize[{-Cos[theta], -Sin[theta], 0}], i d, j d]; (* 入射光の方向ベクトル *)
        qr = trace[{p, v}, m1];
        If[ Length[qr] > 0,
          {q, r} = qr[[1]];
          {showSegment[p, q], showSegment[q, q + 55*r]},
          {showSegment[p, p+40 v]}]
      ],
      {i, -n, n},
      {j, -n, n}
    ],
    PlotRange -> {{-1, 45}, {-10, 10}, {-3, 3}}
  ]
]

このときなので、203.2 mm の 1.5% で焦点距離は ±3.05 mm だけずれる。

をについて解けば、

今の場合はなので、

したがって、のとき、となる。

lines = Module[{
   n = 2,
    d = 0.02,
    f = 20.320,
    theta = 10 Pi/180
  },
  m1 = {{2 f, 0, 0}, 0, 2 f, 
        {Pi-Pi/64, Pi+Pi/64}, {-Pi/64*4, Pi/64*4}};
  indice = DeleteDuplicates[ Table[
        {i, j}, {i, -n, n}, {j, -n, n}
    ] // Flatten[#, 1]& ] // Sort[#, Function[{a,b}, Norm[a]<Norm[b]] ] &;
  Map[
    Function[ij, 
      Module[{i, j, p, v},
        {i, j} = ij;
        p = {2 f Cos[theta], 2 f Sin[theta], 0};              (* 入射光の出発位置     *)
        v = offsetVector[Normalize[{-Cos[theta], -Sin[theta], 0}], i d, j d]; (* 入射光の方向ベクトル *)
        trace[{p, v}, m1]
      ]
    ], 
    indice
  ] // Flatten[#, 1]&
];

Table[
  Show[
    ListPlot[ 
      Map[
         Function[line,
           planeSection[lines[[1]], d, {0,0,1}, line]
         ],
         lines
       ] // Flatten[#, 1] &,
       PlotRange->{{-0.2,0.2},{-0.2,0.2}}
     ],
     Graphics[{Text["d = "<>ToString[d],{-0.15,0.15}, Alignment->Left]}]
  ],
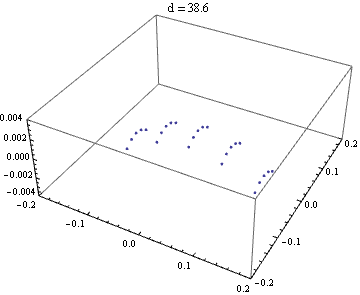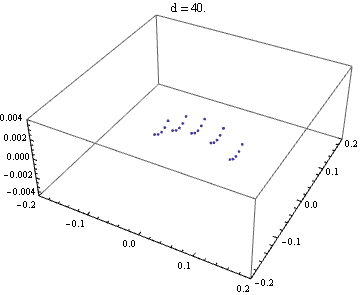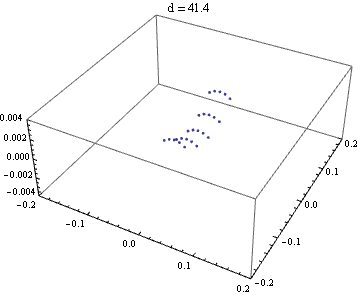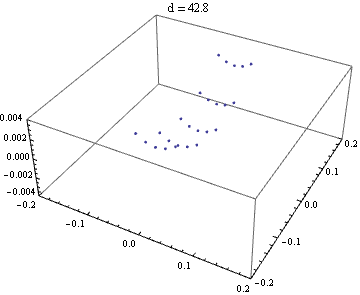
  {d,39.2,42.2,0.2}
]

縦横が一番細くなっているところを読むと、418 - 394 ＝ 24 ≒ 2 * 4 * 3.05 で、計算通りだ。

凸面鏡による補正 †

これを凸面鏡側で補正するには、

焦点距離のミラーであれば、

を満たさなければならないので、例えばだと、

Solve[1/Cos[x] - Cos[x] == 24.7/15, {x}] // N

より、とすればよい。

Module[{
    n = 2,
    d = 0.05,
    f = 3.102/2,
    theta = 61.361 Pi/180,
    m1
  },
  m1 = {{-2 f, 0, 0}, 0, 2 f, 
        {Pi-Pi/4*0.8, Pi+Pi/4*0.8}, {Pi-Pi/4*0.8, Pi+Pi/4*0.8}};
  Show[
    ParametricPlot3D[torusPar[m1, s, t], {s, 0, 1}, {t, 0, 1}], 
    Function[ij, 
      Module[{i, j, p, v, q, r, qrs},
        {i, j} = ij;
        p = offsetVector[{3 Cos[theta], 3 Sin[theta], 0}, i d, j d];
        v = Normalize[{-Cos[theta], -Sin[theta], 0}];
        Map[
          Function[qr,
            Module[{q, r},
              {q, r} = qr;
              {showSegment[p, q], showSegment[q - 4 r, q + 10 r]}
            ]
          ],
          trace[{p, v}, m1]
        ]
      ]
    ] /@ Flatten[
      Array[
        {#1 - n - 1, #2 - n - 1} &, 
        {2 n + 1, 2 n + 1}
      ], 1
    ],
    PlotRange -> {{-2, 5}, {-4, 4}, {-3, 3}}
  ]
]

そうか、斜めに入射すると焦点距離は合わせられても、ビーム形状が楕円になってしまうことは避けられないわけだ。

この角度で入射した場合、

となるから、元のビーム径が 2mm であれば、400 mm 先ではそれぞれ、 113 mm と 25.2 mm まで広がる。後者は良いが、前者は大きすぎる。

しかたがないので焦点距離 25.8 mm の凸面鏡を使うことにすると、入射角は 50.9512°となり、

斜め入射時の焦点距離は 16.2535 mm と 40.9535 mm、
2 mm のビームは 400 mm 先で 49.2 mm と 19.5 mm となる。

これなら何とか使えるか？？？

Module[{
    n = 2,
    d = 0.05,
    f = 2.58,
    theta = 50.9512 Pi/180,
    m1
  },
  m1 = {{-2 f, 0, 0}, 0, 2 f, 
        {Pi-Pi/4*0.8, Pi+Pi/4*0.8}, {Pi-Pi/4*0.8, Pi+Pi/4*0.8}};
  Show[
    ParametricPlot3D[torusPar[m1, s, t], {s, 0, 1}, {t, 0, 1}], 
    Function[ij, 
      Module[{i, j, p, v, q, r, qrs},
        {i, j} = ij;
        p = offsetVector[{3 Cos[theta], 3 Sin[theta], 0}, i d, j d];
        v = Normalize[{-Cos[theta], -Sin[theta], 0}];
        Map[
          Function[qr,
            Module[{q, r},
              {q, r} = qr;
              {showSegment[p, q], showSegment[q - 4 r, q + 10 r]}
            ]
          ],
          trace[{p, v}, m1]
        ]
      ]
    ] /@ Flatten[
      Array[
        {#1 - n - 1, #2 - n - 1} &, 
        {2 n + 1, 2 n + 1}
      ], 1
    ],
    PlotRange -> {{-2, 5}, {-4, 4}, {-3, 3}}
  ]
]

使えるのかどうか・・・ †

そのままだと凹面鏡のスポットサイズが mm 単位まで広がってしまうのはどうか。

さらに、スポットの中で光路長差が激しい（数ミクロン）のも気になる。

数十μｍの光路差はそれだけで 100 fs 単位の遅延時間差を意味する。

もし凹面鏡と凸面鏡の配置を完全に合わせれば補正可能だとしても、三次元的な配置の誤差を考えると現実的ではない気がする。

球面ミラー２枚で使う案２ †

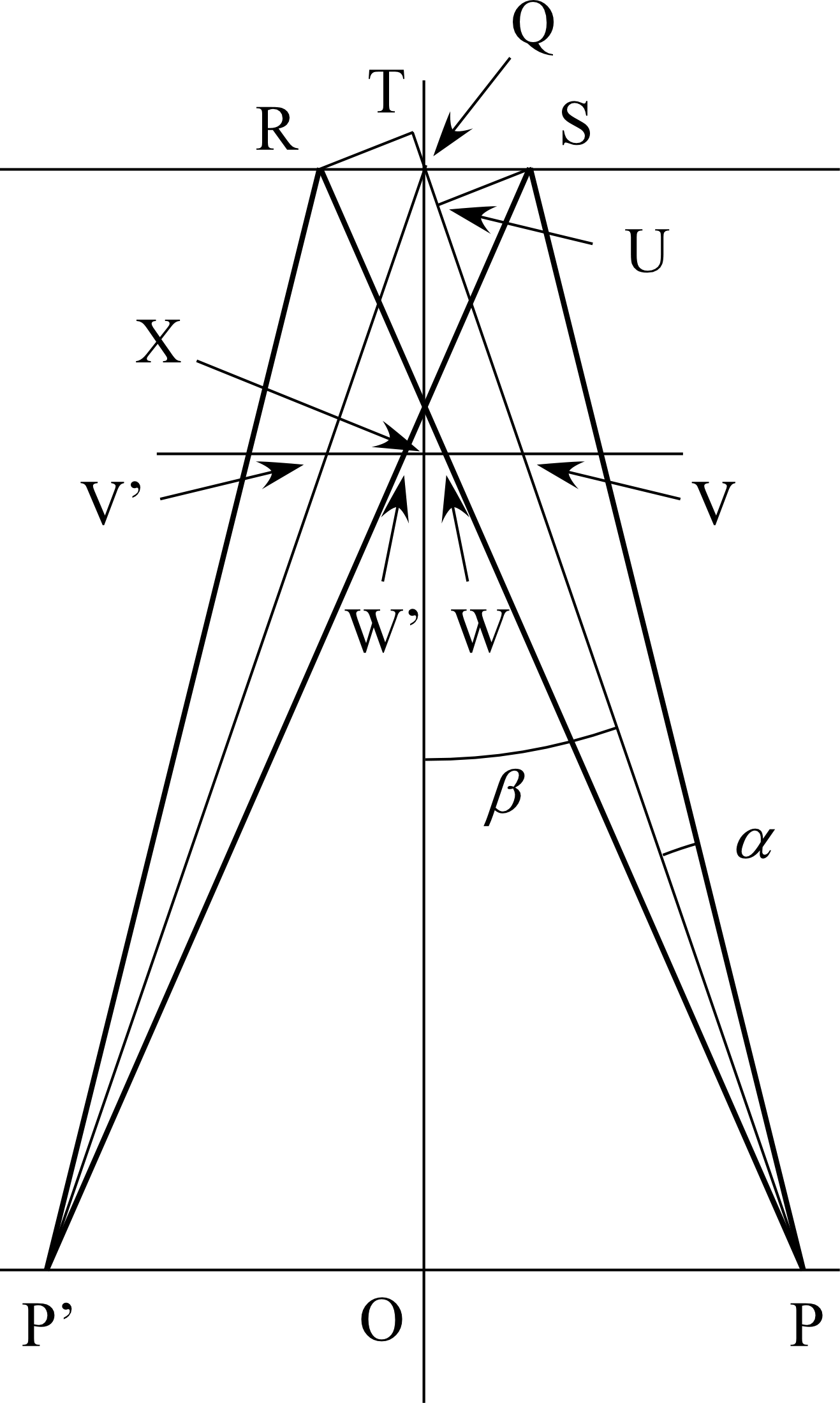
上記の計算では凹面鏡への入射角が大きいと非点収差が大きすぎて厳しいので、入射角をギリギリまで小さくして使うことを考える。

角度を小さくすることでビーム同士が重なってしまうと困るので、凹面鏡上のスポットサイズも小さくしなければならない。

凹面ミラー †

の凹面ミラーを、両側で使う。

ミラー上でのスポットサイズをとすると、

点光源からの広がり全角は、およそ

さらに入射角を程度としてみる。

このとき実際のスポットサイズを計算すれば、

Module[{l, a, b, PQ, OQ , PR, PS, PT, PU, QT, QU, QR, QS},
   l = 406.4;
   a = 10/l/2;
   b = 1/20;
   PQ = l;
   OQ = PQ Cos[b];
   PR = OQ/Cos[b + a];
   PT = PR Cos[a];
   QT = PT - PQ;
   QR = QT/Cos[Pi/2 - b];
   PS = OQ/Cos[b - a];
   PU = PS Cos[a];
   QU = PQ - PU;
   QS = QU/Cos[Pi/2 - b];
   QR + QS
 ]

より 10.013 mm となり、ほぼ計算通り。

ミラーから 106.4 mm の位置、すなわち焦点 P から 300 mm の位置 V において WW' は、

Module[{l,d,l2,a,b,RS,VQ,QX,XW},
   l = 406.4;
   d = 10.013;
   l2 = 300;
   a = 10/l/2;
   b = 1/20;
   RS = d;
   VQ = l-l2;
   QX = VQ Cos[b];
   XW = QX Tan[b+a] - RS/2;
   2 XW
 ]

により、3.2457 mm と求まる。

焦点位置は、

差分は、

計算結果をキャッシュするために、ユーティリティ関数を少し書き換えて、

(* 直線 l がトーラス面 m で反射する様子を追跡する *)
(* 反射点と反射方向ベクトルを返す *)
trace[l_, m_] := 
  Module[{p, v, st, q, n, r}, 
    {p, v} = l; 
    list = intersection[l, m]; 
    Map[ 
      Function[ st,
        q = torusPar[m, s, t] /. st; 
        n = normalVector[m, s, t] /. st; 
        r = reflection[v, n]; 
        {q, r}
      ], list
    ]
  ]

反射の様子を計算する。

(* m1 と lines が設定される *)
lines = Module[{
    n = 2,
    d = 10,
    f = 203.20,
    theta = ArcSin[0.5/10]
  },
  m1 = {{2 f, 0, 0}, 0, 2 f, 
        {Pi-Pi/32, Pi+Pi/32}, {-Pi/32, Pi/32}};
  indice = DeleteDuplicates[ Table[
        {i, j}, {i, -n, n}, {j, -n, n}
    ] // Flatten[#, 1]& ] // Sort[#, Function[{a,b}, Norm[a]<Norm[b]] ] &;
  Map[
    Function[ij, 
      Module[{i, j, p, v},
        {i, j} = ij;
        p = {2 f Cos[theta], 2 f Sin[theta], 0};      (* 入射光の出発位置     *)
        v = offsetVector[
              Normalize[{-Cos[theta], -Sin[theta], 0}], 
              i d / (2 2 f n), j d / (2 2 f n)];      (* 入射光の方向ベクトル *)
        {{p, v}, trace[{p, v}, m1][[1]]}
      ]
    ], 
    indice
  ]
];

計算結果を表示。

Show[
    (* ミラーを表示 *)
    ParametricPlot3D[torusPar[m1, s, t], {s, 0, 1}, {t, 0, 1}], 
    (* 複数の光線に対して計算する *)
    Map[
      Module[{p, v, q, r},
        {{p,v},{q,r}} = #;
        {showSegment[p, q], showSegment[q, q + 450*r]}
      ] &,
      lines
    ],
    PlotRange -> {{-1, 450}, {-40, 40}, {-10, 10}}
  ]

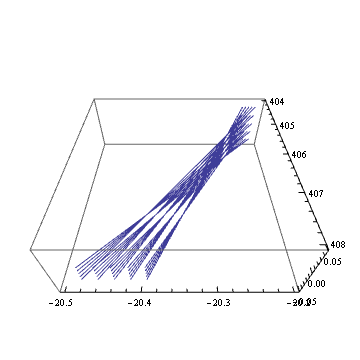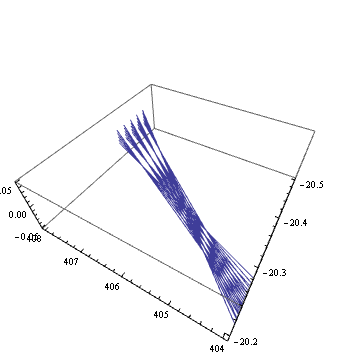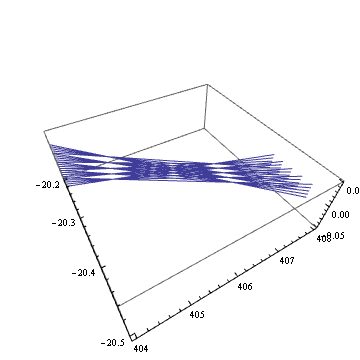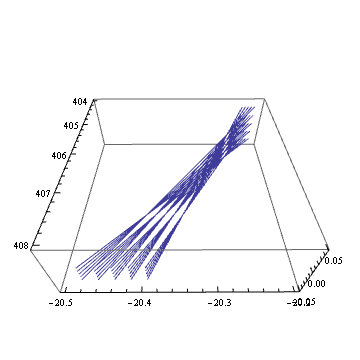
この焦点位置を拡大してみると、

Table[With[{
    n = 3,
    d = 0.1,
    v=RotationTransform[theta,{0,0,1}][{1,0,1}]
  },
   Show[
    (* ミラーを表示 *)
    ParametricPlot3D[torusPar[m1, s, t], {s, 0, 1}, {t, 0, 1}], 
    (* 複数の光線に対して計算する *)
    Map[
     Module[{p, v, q, r},
        {{p,v},{q,r}} = #;
        {showSegment[p, q], showSegment[q, q + 450*r] (*,
	      ListPointPlot3D[Table[
     	    q + (l-Norm[q-p])*r,
	        {l,806,815,0.5}
	      ]] *)
        }
      ] &,
      lines
    ],
    PlotRange -> {{404, 408}, {-20-0.5, -20.2}, {-0.05, 0.05}},
    BoxRatios -> {1,1,1/3},
    ViewPoint -> v,
    ViewAngle -> 65\[Degree]
  ]
], {theta, 0, 2 Pi, 0.02}];
Export["31.gif", % , "GIF"]

確かに、縦横の焦点距離が 2 mm 程度ずれていることが分かる。

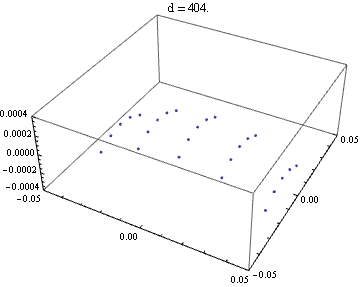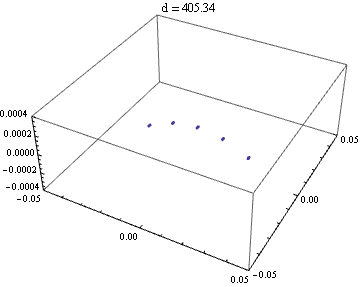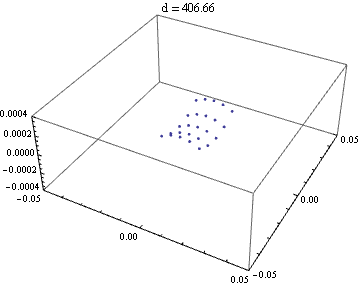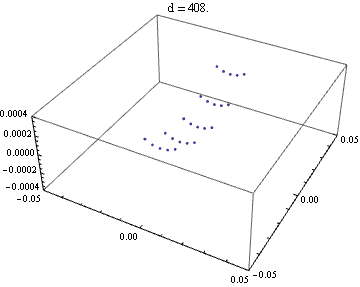
焦点位置近傍での波面は、

Table[
  Module[{l0, r0, u0, l, r, s, t, u},
    {l0, r0} = lines[[1]];
    u0 = Norm[r0[[1]] - l0[[1]]];
    Show[
      ListPointPlot3D[
        Map[
          Function[line, 
            {l, r} = line;
            {s, t, u} = planeSection[r0, d, {0, 0, 1}, r][[1]];
            {s, t, Norm[r[[1]] - l[[1]]] + u - u0 - d}
          ], 
          lines
        ],
        PlotRange -> {{-0.05, 0.05}, {-0.05, 0.05}, {-0.0004, 0.0004}},
        PlotLabel -> "d = " <> ToString[d]
      ]
     ]
   ], 
   {d, 404, 408, 0.01}
 ];
Export["32.gif", % , "GIF"]

ひどく曲がっているようなことはないようだ。

入射角を小さくすることで非点収差を大幅に押さえられることが分かる。

凸面ミラー †

を、一方を平行光線、もう一方を拡散光線として用いる。

焦点間距離をとするためには、

Solve[104.6 (1/Cos[x] - Cos[x]) == 2.034, {x}]

とすればよい。

lines = Module[{
    n = 2,
    d = 1,
    f = 104.6,
    theta = 0.13922
  },
  m1 = {{-2 f, 0, 0}, 0, 2 f, 
        {-Pi/32, Pi/32}, {-Pi/32, Pi/32}};
  indice = DeleteDuplicates[ Table[
        {i, j}, {i, -n, n}, {j, -n, n}
    ] // Flatten[#, 1]& ] // Sort[#, Function[{a,b}, Norm[a]<Norm[b]] ] &;
  Map[
    Function[ij, 
      Module[{i, j, p, v},
        {i, j} = ij;
        p = offsetVector[
          {2 f Cos[theta], 2 f Sin[theta], 0},     (* 入射光の出発位置     *)
          i d / (n), j d / (n)];
        v = Normalize[{-Cos[theta], -Sin[theta], 0}]; (* 入射光の方向ベクトル *)
        {{p, v}, trace[{p, v}, m1][[1]]}
      ]
    ], 
    indice
  ]
];

Show[
  (* ミラーを表示 *)
  ParametricPlot3D[torusPar[m1, s, t], {s, 0, 1}, {t, 0, 1}], 
  (* 複数の光線に対して計算する *)
  Map[
    Module[{p, v, q, r},
      {{p,v},{q,r}} = #;
      {showSegment[p, q], showSegment[q-130*r, q + 100*r]}
    ] &,
    lines
  ],
  PlotRange -> {{-120, 120}, {-40, 40}, {-10, 10}}
]

焦点部分は、

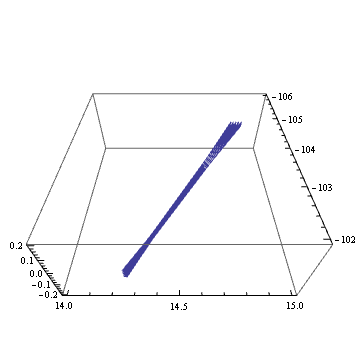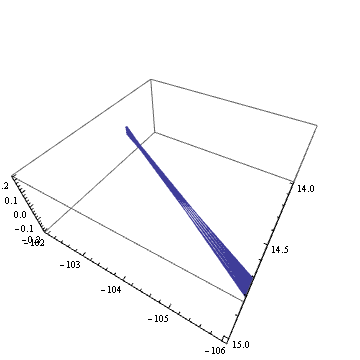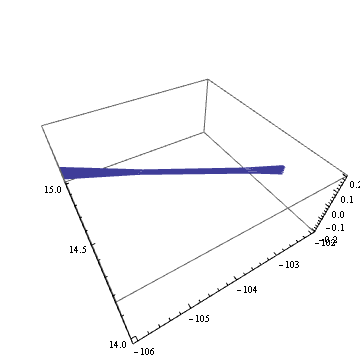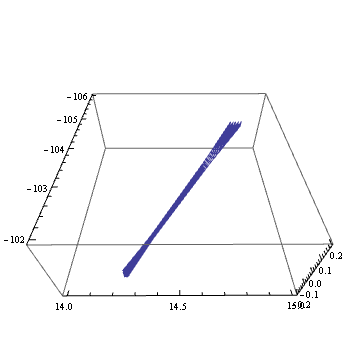
Table[
  Show[%,
    PlotRange -> {{-106, -102}, {14, 15}, {-0.2, 0.2}},
    BoxRatios->{1,1,2/5},
    ViewPoint -> RotationTransform[theta,{0,0,1}][{1,0,1}],
    ViewAngle -> 65\[Degree]
  ], {theta, 0, 2 Pi, 0.02}
];
Export["34.gif", % , "GIF"]

Counter: 17829 (from 2010/06/03), today: 1, yesterday: 0