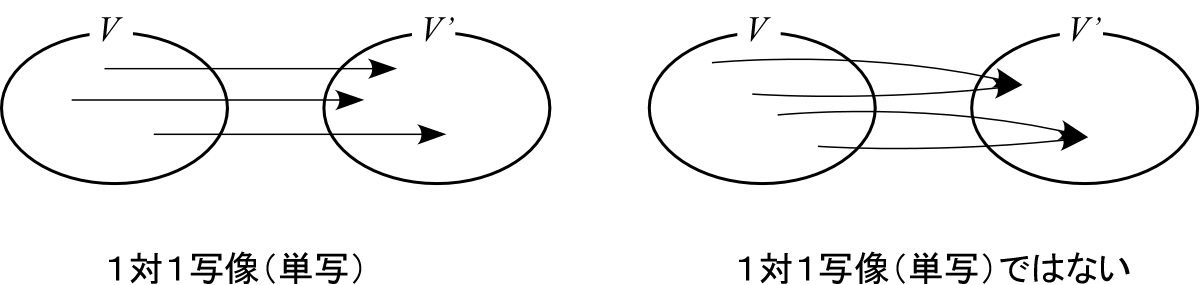線形代数II/抽象線形空間 のバックアップ(No.6)

更新

線形代数Ⅱ?

「線形代数学」の意味 †

１年生の線形代数Ｉにおいて、「線形」の意味を教わった。

関数 f(\bm x) が線形　：　 f(a \bm x+b \bm y)=a f(\bm x)+b f(\bm y) が成り立つこと

では「代数学」とは何だろうか？

小学生から大学１年生まで、様々な「数」を学んだ。

  • \mathbb N 自然数 = 加算・乗算について閉じている　 a+b, a\times b
  • \mathbb Z 整数　 = 減算についても閉じている a-b
  • \mathbb Q 有理数 = 除算について「ほぼ」閉じている a/b （ゼロは例外）
  • \mathbb R 実数　 = 収束する有理数列の極限演算について閉じている \lim_{n\rightarrow\infty}a_n
  • \mathbb C 複素数 = 負数の開根操作について閉じている \sqrt{-1}

知っての通り \mathbb N \subset \mathbb Z \subset \mathbb Q \subset \mathbb R \subset \mathbb C であり、これまでの数学では新しい「演算」の導入により「数の集合」を拡大する方向で学んできた。

  • 解析学は主に \mathbb C の上（あるいは \mathbb C^n の上）で 極限や微積分を扱う数学である

代数学は \mathbb N, \mathbb Z, \mathbb Q, \mathbb R, \mathbb C の系列から外れて、
例えば、

乗算は定義されるが加算は定義されない数の集合

などというように、「何らかの演算」が定義された「数の集合」を定め、 そこに現れる「構造」を研究する学問である。

これから学ぶ「ベクトル」も上で言う「数」の一員である。

代数学的構造の例：　群 †

ある集合 \mathbb U にある演算 * が定義され、 \mathbb U は * について「閉じている」とする。
(すなわち \forall x,\forall y \in \mathbb U について x*y\in \mathbb U )

さらにこの演算が次の性質を持つ時、

  1. \forall a,\forall b,\forall c\in \mathbb U に対して結合法則 (a*b)*c=a*(b*c) が成り立つ
  2. \forall x \in \mathbb U に対して e*x=x*e=x を満たすような特別な元（単位元） e\in \mathbb U が存在する
  3. \forall x \in \mathbb U に対して、 x*y=y*x=1 を満たすような元（逆元） y\in \mathbb U が存在する

「 \mathbb U は演算 * について群である」という。

群の例 †

一見すると、 \mathbb U を有理数 \mathbb Q 、 * を通常の乗算 \times と考えれば 「群の公理」を満たしそうに思えるが、 0\in \mathbb Q が逆元を持たないため、 有理数 \mathbb Q は乗算 \times について群とはならない。

\mathbb U を有理数 \mathbb Q からゼロを除いた集合 \mathbb Q-\set{0} 、 * を通常の乗算 \times 、単位元を 1 とすれば、この集合は群である。

また、 \mathbb U を整数 \mathbb Z 、 * を通常の加算 + 、単位元を 0 と考えると、この場合も上記３つすべての条件を満たすことから、 \mathbb Z は加算について群である。

また、 \mathbb U を k の倍数 \set{nk|n\in \mathbb Z} 、 * を通常の加算 + 、単位元を 0 と考えると、この場合も上記３つすべての条件を満たし、群を為す。

群の要素数が有限である場合もある。

自明な群： \mathbb U={1} に対して、 1*1=1 と定義すれば、 \mathbb U は群である。

\mathbb U={a,b,c} に対して、演算 * を

*abc
aabc
bbca
ccab

と定義すれば、 \mathbb U は群である。
ただしこの表は、 (左に書かれた数)*(上に書かれた数) の演算結果を示した物である。

群の公理を気にしなければ、「演算」はこのように適当に表を作れば定義できる。

しかしこの表を、

*abc
aabc
bbcb
ccba

としてしまえば、 (c*b)*b=b*b=c\ne c*(b*c)=c*b=b となって、 \mathbb U は群ではなくなる。

「群」の公理は上のように単純なものであるが、 その数学的構造は非常に奥深く、群論だけで数学の１分野となる。
応用理工では群論の詳細には立ち入らないが、 結晶学や分子振動における点群や、 ゲージ理論などにおける対称性に関する議論に重要な応用があるため どこかでまた学ぶことになるかもしれない。

その他の代数的構造 †

  • 半群 = 群の公理から 2., 3. を除いて 1. のみを公理とする
  • 群 = 上記
  • 可換群 = 群の公理に交換律 a*b=b*a を加える
  • 環 = ２つの演算 +,* を持ち、 + に対して可換群、 * に対して半群であり、分配法則 a*(b+c)=a*b+a*c が成立する
  • 体 = 環でありかつ * に対しても、0 を除いて可換群である（つまり、四則演算ができる）

これ以外にも数多くの代数的構造が研究されている。

有理数 \mathbb Q や実数 \mathbb R 、複素数 \mathbb C は 自由に四則演算の行える構造を持ち、「体」である。 そこでしばしば 有理体、実数体、複素数体 などとも呼ばれる。

代数的構造の意味 †

「代数的構造」の優れた点は数学的に類似の構造を持つ対象を抜き出して、 それらをまとめて議論できる点にある。

「類似点」を公理の形で記し、公理のみを基に定理を導くことにより、 個々の対象に依存せず、すべての対象に適用可能な結論を導ける。

4-1 線形空間 (あるいは ベクトル空間) †

線形代数I では主に数ベクトルについて学んだ。

「線形空間」は 数ベクトル に類似した「代数的構造」を表わす概念である。

定義 †

まず、ある既知の「体」 K を想定する。

K=\mathbb R\ \mathrm{or}\ \mathbb C であることが多いが、加減乗除が可能であれば他の体でも良い

  • 線形空間 V は集合であり、その元をベクトルと呼ぶ
    すなわち、 \bm x,\bm y\in V なら \bm x,\bm y はベクトル
  • ２つのベクトルの間に「和」が定義され、 V はベクトルの和に対して閉じている
    すなわち、 \forall\bm x,\forall\bm y\in V に対して \bm x+\bm y\in V
  • K の元とベクトルとの間に「スカラー倍」が定義され、 V はスカラー倍に対して閉じている
    すなわち、 \forall\bm x\in V 、 \forall a\in K に対して a\bm x\in V

さらに、これらの「和」と「スカラー倍」に対して次の公理が成立する。

  1. \forall \bm x,\forall \bm y\in V について \bm x+\bm y=\bm y+\bm x 　　　　　　　　　　　　　　→ ベクトル和に対する交換律
  2. \forall \bm x,\forall \bm y,\forall \bm z\in V について (\bm x+\bm y)+\bm z=\bm x+(\bm y+\bm z) 　　　→ ベクトル和に対する結合律
  3. \forall \bm x\in V について \bm x+\bm 0=\bm x を満たす元 \bm 0\in V が存在　→ ゼロ元の存在
  4. 1\in K について、 \forall \bm x\in V について、 1\bm x=\bm x 　　　　　　　　　　　→ スカラーの単位元
  5. \forall \bm x\in V について \bm x+(-\bm x)=\bm 0 を満たす元 -\bm x\in V が存在　→ 逆元の存在
  6. \forall a,\forall b\in K 、 \forall \bm x\in V について、 (a+b)\bm x=a\bm x+b\bm x 　　→ 分配法則(1)
  7. \forall a\in K 、 \forall \bm x,\forall \bm y\in V について、 a(\bm x+\bm y)=a\bm x+a\bm y 　→ 分配法則(2)
  8. \forall a,\forall b\in K 、 \forall \bm x\in V について、 a(b\bm x)=(ab)\bm x 　→ スカラー倍の結合則

このとき、 V を K 上の線形空間と呼ぶ。

線形代数Ⅱ/抽象線形空間/練習?

線形空間の例 †

V=\mathbb R^3,K=\mathbb R は線形空間である

V=\mathbb R^3,K=\mathbb C は線形空間ではない！

V=\set{ax^2+bx+c|a,b,c\in \mathbb R}, K=\mathbb R （ x の２次以下の実係数多項式の集合）は、自然に定義される和と実数倍に対して線形空間となる

V=\set{(3a,-a)\in \mathbb R^2|a\in \mathbb R} は \mathbb R^2 に定義される和と実数倍に対して線形空間となる

このような一般の線形空間 V がどこまで \mathbb R^n と似ているかを考えるのが以下の目標となる。

線形空間の公理の使い方 †

ベクトルの差 †

上の線形空間の定義にはベクトルの和は定義されているが、差は定義されていない。

そこで、ベクトルの差を \bm x-\bm y=\bm x+(-1)\bm y と定義する。

問：任意の \bm x\in V に対して \bm x-\bm x=\bm 0 を満たすことを証明せよ。
答： \bm x-\bm x=1\bm x+(-1)\bm x=(1-1)\bm x=0\bm x=\bm 0

一次独立・従属 †

\bm v_1,\bm v_2,\dots,\bm v_m\in V が「一次独立である」とは、

\sum_{i=1}^m c_i\bm v_i=c_1\bm v_1+c_2\bm v_2+\dots+c_m\bm v_m=\bm 0 から　 c_1=c_2=\dots=c_m=0 を導けることを表わす

\bm v_1,\bm v_2,\dots,\bm v_m\in V が一次独立では無いとき、一次従属であると言う。

一次独立／従属の概念は公理で定義された演算のみで定義されており、 ベクトルの実態に関する知識が必要ないことに注目。

問：実数を係数とする２次以下の x の多項式の集合について考える V=\set{ax^2+bx+c|a,b,c\in \mathbb R}
x^2+3x-2, -x^2+2x, 3x^2 は線形独立か？

答： a(x^2+3x-2)+b(-x^2+2x)+c(3x^2)=0 とすると、 (a-b+3c)x^2+(3a+2b)x+(-2a)=0
すなわち、 a-b+3c=0,3a+2b=0,-2a=0 となり、これを満たす a,b,c は \{a,b,c\}=\{0,0,0\} しか存在しない。
したがって、線形独立である。

同型な線形空間 †

実数を係数とする３次以下の x の多項式３次実数ベクトル
&math(V=\set{ax^3+bx+c\a,b,c\in \mathbb R});&math(\mathbb R^3=\set{(a,b,c)\a,b,c\in \mathbb R});
(a_1x^3+b_1x+c_1)+(a_2x^3+b_2x+c_2)\\=(a_1+a_2)x^3+(b_1+b_2)x+(c_1+c_2) (a_1,b_1,c_1)+(a_2,b_2,c_2)=(a_1+a_2,b_1+b_2,c_1+c_2)
k(ax^3+bx+c)=(ka)x^3+(kb)x+(kc) k(a,b,c)=(ka,kb,kc)

すごく似ている。

こういう時、 V と \mathbb R^3 は「同型である」、と言う。

以下で同型を定義する。

写像 †

T は線形空間 V から V' への写像であるとする。
すなわち T は、任意の \bm v\in(V) に対して、ただ１つの \bm v'\in V' を \bm v'=T(\bm v) として定める。

線形写像 †

T が次の２つの条件を満たすとき、 T は線形である、と言う。

  • T(\bm x+\bm y)=T(\bm x)+T(\bm y)
  • T(c\bm x)=cT(\bm x)

ここで、 左辺の和やスカラー倍が V で定義された演算であるのに対して、
右辺の和やスカラー倍は V' で定義された演算であることに注意せよ。

（すなわち V と V' は同じスカラーの上に定義されている）

上の例で言えば、

T(ax^2+bx+c)=(a,b,c) は V\rightarrow\mathbb R^3 の線形写像である。

練習 †

問： T が線形写像であれば、 T(\bm 0)=\bm 0 となることを示せ。

答： T(\bm 0)=T(0\bm 0)=0T(\bm 0)=\bm 0

１対１写像（単写） †

T(ax^2+bx+c)=(a,b,0) も V\rightarrow\mathbb R^3 の線形写像である、 が、 T(ax^2+bx+c)=T(ax^2+bx+c')=(a,b,0) となる。

このように、一般の写像では異なるベクトルが同じ値に移される場合がある。

\bm x\ne \bm y であれば必ず T(\bm x)\ne T(\bm y) であるとき、 T は１対１写像である、あるいは、単写である、と言う。

写像.png

１対１という言葉の意味：１対ｎはそもそも写像にならない。ｎ対１になっていないことを示している。

上への写像（全写） †

任意の v'\in V' に対して、そこに移ってくる V の元を見つけられる時、 上への写像、あるいは、全写であるという。

例えば、 T(ax^2+bx+c)=(a,b,c) は V\rightarrow\mathbb R^3 への全写であるが、
T(ax^2+bx+c)=(0,a,b,c) は V\rightarrow\mathbb R^4 への全写ではない。

「上へ」というのは、 T により V 全体を移したときにできる「像」 (しばしば T(V)=\set{T(\bm v)\in V'|\bm v\in V} と書かれる) が、 V' の真上に、全体を覆い尽くすように被さるため。

上への写像.png

上への１対１写像（全単写） †

単写かつ全写であることを言う。

このときに限り、「逆写像 T^{-1} 」が定義できる。

  • １対１でないと、ある v'\in V' に複数の v\in V が対応してしまう
  • 上への写像でないと、ある v'\in V' に対応する v\in V が存在しない場合がある

練習 †

問：逆写像 T^{-1} は線形写像であることを示せ

答： \bm X=T(\bm x), \bm Y=T(\bm Y) とすると、 \bm x=T^{-1}(\bm X),\bm y=T^{-1}(\bm Y)

一方、

T(\bm x+\bm y)=T(\bm x)+T(\bm y)=X+Y

の両辺に T^{-1} を作用させると

\bm x+\bm y=T^{-1}(X)+T^{-1}(Y)=T^{-1}(X+Y)

また、

T(k\bm x)=kT(\bm x)=kX

の両辺に T^{-1} を作用させると

k\bm x=kT^{-1}(X)=T^{-1}(kX)

となって、 T^{-1} が線形であることが示された。

同型 †

V と V' との間に上への１対１写像 T が存在する時、 V と V' は同型であるといい、
V\simeq V' と書く。

またこのとき、 T を同型写像と呼ぶ。

これは上で述べた２つの写像が「似ている」ことを数学的に表わした物。
同型写像によって、２つの空間はすべて１対１に対応することになる。

T(ax^2+bx+c)=(a,c,b) とか、
T(ax^2+bx+c)=(a+b,a-b,c) とかも同型写像になる。 同型である２つの線形空間の間の同型写像は一意には決まらないことに注意が必要。

線形空間の「同型」は同値関係の公理を満たす。すなわち、

  1. V\simeq V 　　　：　反射律
  2. V\simeq V'\to V'\simeq V 　：　対称律
  3. V\simeq V' \wedge V'\simeq V''\to V\simeq V'' ：　推移律

同型の線形空間は構造が似ているため、一方を調べればもう一方のことが分かる。
特に、 \mathbb R^n への同型が分かればほぼすべて分かったも同然！となる。

例 †

V\to V' の同型写像を T(\bm x) とする。

\bm a, \bm b, \bm c\in V が線形独立であれば、
[Math Conversion Error]


も線形独立である。

対偶を証明する。

もし [Math Conversion Error]


が線形従属であれば、 すべてがゼロではない３つのスカラー \alpha,\beta,\gamma に対して

[Math Conversion Error]


が成立する。 T は線形なので、

[Math Conversion Error]


ここで、

\therefore T^{-1}(\bm 0)=\bm 0

4-2 線形独立、基底及び次元 †

あるベクトル \bm v\in V をベクトル a_1,a_2,\dots,a_l の一次結合で表せる場合と、表せない場合がある。

Counter: 23942 (from 2010/06/03), today: 2, yesterday: 5