量子力学Ⅰ/波動関数の解釈 のバックアップ(No.6)
更新- バックアップ一覧
- 差分 を表示
- 現在との差分 を表示
- ソース を表示
- 量子力学Ⅰ/波動関数の解釈 へ行く。
量子力学I?
波動関数の物理的な意味は何か? †
シュレーディンガー方程式が正しいとして、そこから求まる波動関数の物理的意味は何であろうか?
話の進み方が奇妙? †
近代の物理学ではこのように、「正しそうな方程式が先に求まって、後からその意味を考える」 という手順を踏むことがしばしばある。
「直感的に理解できる」方程式が基礎となっていた古典論と比べると、 このようなやりかたは始め奇妙に思えるが、 量子力学の真価が現れるような極小の世界に対しては我々の「直感の働かない」のだからしかたがない、 と考えて納得してほしい。 実際これから直感とはかけ離れた物理現象を学ぶことになる。
- 観測された物理現象を説明できそうで、かつ論理的に矛盾のない基礎方程式を適当にでっち上げる
- その方程式から何が予測されるかを考えて、新たな測定結果と突き合わせる
- 矛盾が生じれば理論に修正が必要となる
- 矛盾無く測定結果を説明できている限り、それが正しい理論である
このような意味で現在受け入れられているのが、
先に 求めた でっち上げた シュレーディンガー方程式である。
測定される物理現象 †
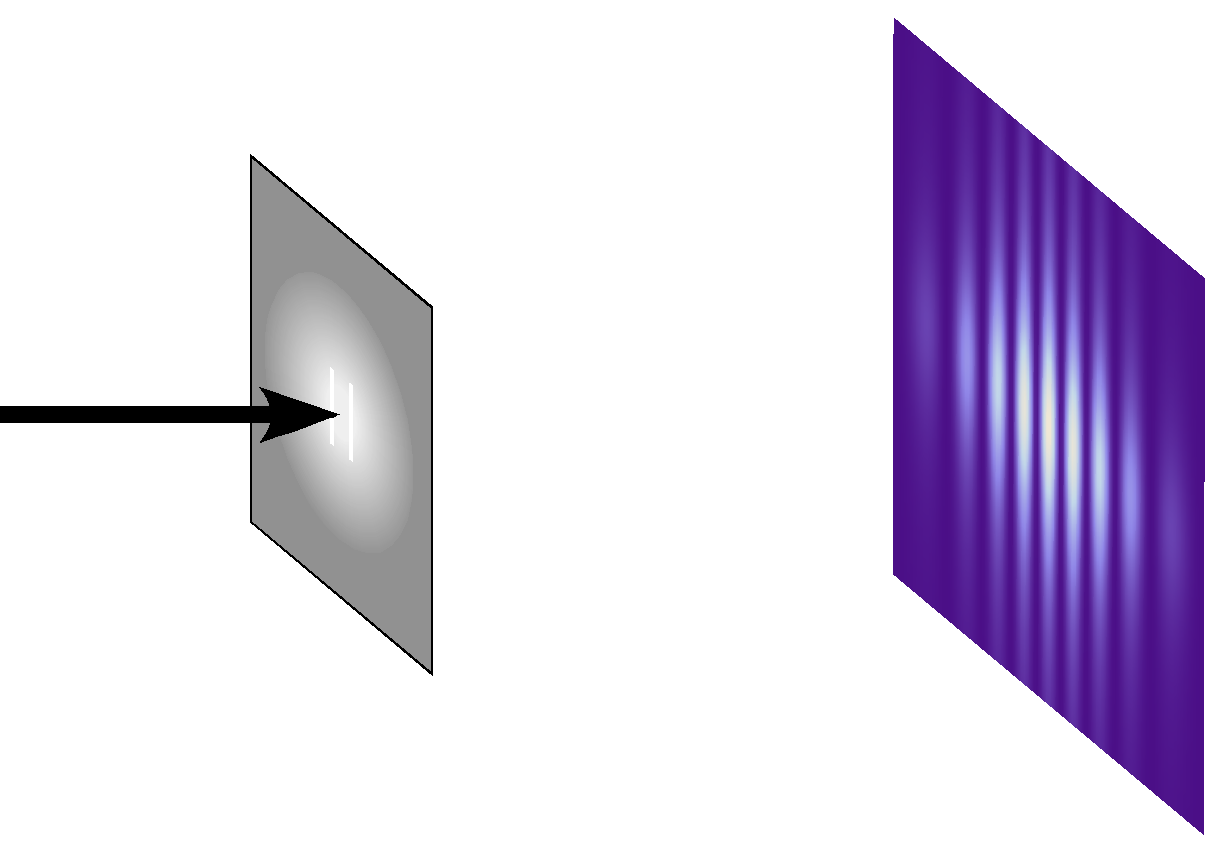
電子の波動関数の意味を理解する上で最も分かりやすい実験結果の1つに、 二重スリットを通る電子についての測定が挙げられる。
二重スリットの実験は光学でもよく知られており、ホイヘンスの原理によれば、 スリット後の状況は2つのスリットの位置にそれぞれ点光源があるのと同じであり、 それらの光の干渉によりスクリーン上に干渉縞が現れる。 当然、片方のスリットを閉じれば干渉縞は消失する。
電子に対しても同様の実験を行うことができて、その結果、光と同様に干渉縞が現れる。
電子が古典的な粒子であればスリットを通った電子は単に直進するのみであるから、 もう一方のスリットが開いていようが閉じていようが 1つのスリットを通った電子がスクリーン上に到達する位置は変わらないはずで、 二重スリットの結果は単一スリットの結果の足し算になるはずである。
それにもかかわらず干渉縞が現れることは、確かに電子が波の性質を持っていることを表わしてる。
それでは電子に粒子としての性質が無いのかといえばそんなことはない。 高感度のスクリーンを用いることで、 1つ1つの電子がスクリーン上に到達した位置を記録することができる。 干渉縞が現れる場合にも、1つの電子は1つの点に到達する。 すなわち、電子は確かに粒子なのである。
有名な
コペンハーゲン解釈 †
現在受け入れられている波動関数の解釈は以下のような物である。コペンハーゲンにあるボーア研究所で主に構築されたため、コペンハーゲン解釈と呼ばれる。*1歴史的にはこの解釈がなされた時点で上記のような顕著な実験結果は得られておらず、この解釈が受け入れられるまでにはかなりの紆余曲折があった
- 電子の時間発展はシュレーディンガー方程式を満たす波動関数 で記述される
- 波動関数は空間的に広がりを持ち、また、干渉や回折などの波に特有な性質を現す
- 電子の位置を実験的に観測した場合には電子はある一点に見出される
- 位置 に電子が発見される確率は に比例する
二重スリットの実験に当てはめれば、
- 二重スリットを通る電子の波動関数は、2つのスリットのそれぞれを通る経路の間で干渉を起こす
- その結果、波動関数の絶対値の二乗 に干渉縞が現れる
- 電子がスクリーンに当たり、その位置が記録されることが「観測」にあたる
- 観測される電子位置は常に1点だけに定まり、広がりを持たない
- の大きな箇所でより多くの電子が発見されるため、 多くの電子について観測を繰り返すことによりスクリーン上に干渉縞が現れる
空間的に広がりを持つ電子が観測により1点に見出される様子は「波動関数の収束」と呼ばれる。
現在の量子力学は、なぜ観測により波動関数が収束を起こすのか、 とか、観測しないときに電子はどの位置にあるのか、といった問いには答えない。 「観測によって検証できない内容」は物理の範疇ではないというスタンスである。
そのかわり、「観測により確かめられる内容」については量子力学は完璧な予想を与える。 (対応するシュレーディンガー方程式が数学的に解ける範囲にある限り)
確率密度関数について †
波動関数の絶対値の二乗 は時刻 において位置 に電子を見出す確率密度関数となる。
確率・統計の需要を取った学生には学習済みの内容であるが、 確率密度関数についてここで復習しておく。
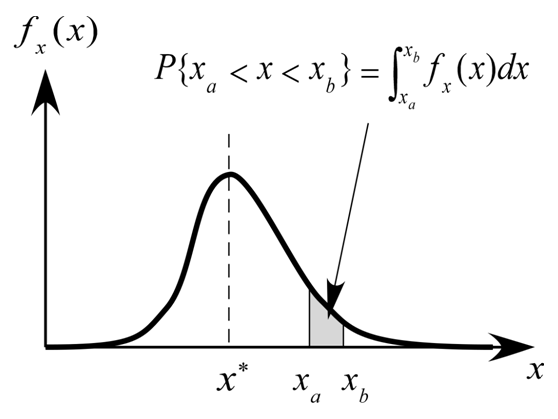
確率密度関数の定義 †
「確率変数 が確率密度関数 に従う」という意味は、
測定毎に異なる値を取る変数 があり、1回測定したときに が の範囲に入る確率を
として求められる、ということである。
右図で分かるとおり、上式の右辺の積分は と 軸に挟まれる部分の面積に相当するため、 が大きいことは がその付近の値を取りやすいことを表わしており、 が小さければ はその付近の値を滅多に取らない。
当然、すべての に対して であり、 また、測定を行えば必ず何らかの値が得られることから、 を全範囲にわたって積分した値は常に1になる。
期待値 †
確率変数 の測定を仮想的に無限回行った場合に得られる平均値を の期待値という。
例えば、サイコロを1回振った際に出る目の期待値は、
のように、サイコロの目の値に、個々の目の出る確率を掛けて得られる。
すなわち、離散的な値を取る確率変数 の期待値 は、
として与えられる。ここで は となる確率である。
いま考えている が連続値を取る場合にも、これと同様に
により期待値が求まる。測定値が範囲 に入る確率を と表せることに注意せよ。
標準偏差 †
標準偏差は確率変数 がその期待値からどれほど大きなバラツキを持つかを表わす指標である。
統計学的には、 回の測定値 の標準偏差は、
として定義される。
これに対して確率変数 を仮想的に無限回観測した際の標準偏差の期待値は
として求められる。これを確率密度関数 の標準偏差という。
任意の関数の期待値 †
標準偏差の場合と同様に、確率変数 の関数として表わされる任意の値 の期待値を、
として求められる。 が線型である場合を除き、
であることに注意せよ。
複合確率 †
確率変数
が区間
に入る確率が
であり、
確率変数
が区間
に入る確率が
であり、
両者が同時に起きる確率が
であるとする。
「 と が独立ならば」 である。
「 と に相関があれば」 である。
波動関数から各種物性値を取り出すには †
シュレーディンガー方程式を解いて波動関数 が得られたとする。 この波動関数から電子の運動について何をどのように知ることができるのだろうか?
波動関数の規格化 †
シュレーディンガー方程式は線型な方程式だから、 ある関数 が解であれば、 任意の定数 に対して も解である。
一方、波動関数の絶対値の二乗が確率密度関数となるためには、
でなければならない。
任意のシュレーディンガー方程式の解 に対して、
を掛けることで
のように波動関数の規格化し、 が確率密度関数になるようにできる。
全確率の保存 †
ある時刻において規格化した波動関数がシュレーディンガー方程式に従って時間発展する時、 確率密度が増えたり減ったりしてはおかしなことになる。この点を確認しよう。
&math( \frac{d}{dt}\iiint|\psi(\bm r,t)|^2\,d\bm r &=\iiint\psi^*\frac{\PD\psi}{\PD t}+\frac{\PD\psi^*}{\PD t}\psi\,d\bm r\\ &=\frac{i\hbar}{2m}\iiint\psi^*(\nabla^2\psi)-(\nabla^2\psi^*)\psi\,d\bm r\\ &=\frac{i\hbar}{2m}\iiint\bm \nabla\cdot\big[\psi^*(\bm \nabla\psi)-(\bm \nabla\psi^*)\psi\big]\,d\bm r\\ &=\frac{i\hbar}{2m}\iint_S\big[\psi^*(\bm \nabla\psi)-(\bm \nabla\psi^*)\psi\big]\cdot \bm n\,dS\\ );
最後の等式はガウスの定理を用いて体積積分を面積積分に直した。 ここでは積分範囲を無限大に取っているためその表面というのは考えづらいが、 が有限範囲内のみゼロでない値を取る場合を想定し、 それより大きな範囲を取ると考えれば問題ない。
そのような場合、表面 上で積分内の関数はゼロになるため、
シュレーディンガー方程式に従った時間発展では全確率密度が保存されることが分かった。
確率密度の流れ †
上記の計算において積分領域を有限に取れば、 右辺の積分は領域外から領域内へ入ってくる確率密度であると解釈できる。*2ピンと来なければ電磁気学で学んだ電荷の保存則の部分を復習せよ すなわち、積分内の符号を反転した
&math( \bm S(\bm r,t)&=-\frac{i\hbar}{2m}\big[\psi^*(\bm \nabla\psi)-(\bm \nabla\psi^*)\psi\big]);
あるいはこれを変形した、
&math( \bm S(\bm r,t)&=\frac{\hbar}{2mi}\big[\psi^*(\bm \nabla\psi)-\{\psi^*(\bm \nabla\psi)\}^*\big]\\ &=\frac{\hbar}{2mi}\cdot 2\,\mathrm{Im}\Big[\psi^*(\bm \nabla\psi)\Big]\\ &=\mathrm{Re}\Big[\psi^*\frac{\hbar\bm \nabla}{mi}\psi\Big]\\ );
が局所的な確率密度の流れを表わす(単位面積当たり、単位時間当たりの流量)。
多数の電子が同じ波動関数に従って移動しているような場合には、 この に素電荷 を掛けた物が電流密度になるなど、 物理的な意味も大きい。
座標について †
が確率密度関数であるならば、 電子の位置の 座標の期待値 は
として求められる。
二重スリットの実験のように電子の存在確率が広範囲に広がっている場合には この期待値にあまり意味はない。一方、ポテンシャルにより束縛された電子や、 波束として空間中を飛ぶ電子ではこれがそのまま電子の位置の時間変化を表わすことになる。
もちろんその場合にも波動関数は広がりを持つから、任意の時刻の波動関数の広がりを評価するために 座標の標準偏差の期待値を求めるようなことも意味を持つ。
このように一旦波動関数が求まれば、座標 の関数 として表わされる任意の関数について、
としてその期待値を求めることが可能である。
運動量について †
量子力学によれば、 電子の位置が確率的にしか決定されないのと同様に、 その運動量も確率的にしか決定されない。
位置の確率密度関数は波動関数により与えるとして、 運動量の確率分布はどのようなものになるだろうか?
シュレーディンガー方程式をでっち上げた際に、平面波に対して および が成り立つことを利用した。
実は平面波でない場合にも、運動量 の期待値を、
&math( \langle \bm p(t)\rangle=\iiint \psi^*(\bm r,t) (\hbar\bm \nabla/i) \psi(\bm r,t)\,d\bm r );
として求めることができる(こうして求めると実験と合う)。 左から がかかっているのは、 であることに対応している。
同様に、 の関数で与えられる任意の物性値 の期待値は、 の中の を で置き換えた演算子 を作り、
&math( \langle g(\bm p)\rangle=\iiint \psi^*(\bm r,t) \hat g(\hbar\bm\nabla/i) \psi(\bm r,t)\,d\bm r );
とすれば求められる。
一般の場合 †
解析力学の授業において、1つの粒子の運動は座標と運動量によって完全に記述されることを学んだ。
すなわち電子の運動を表わす任意の物性値は座標と運動量の関数として の形に書ける。波動関数からこのような物性値の期待値を求めるには、 を で置き換えた演算子 を作り、
&math( \langle g(\bm r,\bm p)\angle=\iiint \psi^*(\bm r,t) \hat g(\bm r,\hbar\bm\nabla/i) \psi(\bm r,t)\,d\bm r );
とすればよい。
このようにして求めた の期待値が実数になることはそれほど自明ではない。 後に任意の物理量を表わす演算子がエルミートになることを使って期待値が実数になることを理解する。
確率密度の流れ(再) †
は運動量を表わす演算子であり、 はそれを質量 で割った物であるから、 よりこれは速度を表わす演算子となる。すなわち、確率密度の流れを
&math( \bm S(\bm r,t)&=\mathrm{Re}\Big[\psi^*\hat{\bm v}\psi\Big]\\ );
と書いておくと覚えやすい。
不確定性原理 †
量子力学の重要な帰結として「不確定性原理」がある。
不確定性原理は例えば、「 と が同時に正確に定まるような状態は存在しない」という形で言い表せる。
計算の詳細は別掲するとして?、シュレーディンガー方程式より導かれる結果は次のようになる。
&math( \sigma_x\cdot\sigma_{p_x} = \sqrt{\big\langle (x-\langle x\rangle)^2\big\rangle} \sqrt{\big\langle (p_x-\langle p_x\rangle)^2\big\rangle} \ge \frac{\hbar}{2} );
どんな波動関数に対してもこの不等式が成り立つことは、 そもそも電子自身が「上記の不等式以上に定まった位置や運動量を持つことがない」 ことを示している。
このことと、位置や運動量を測定する際にどうしても有限の誤差を生じるため、 位置や運動量を「測定によって正確に決定できない」ということとは、 しばしば混同して議論されるが、本来異なる話であるため分けて考える必要がある。
実際、ハイゼンベルグが当初議論したのは位置 を測定する際の測定誤差 と、 その位置の測定により運動量 が受ける撹乱 の積 に関するものであり、ハイゼンベルグの思考実験においては が得られた。
しばしば量子ゆらぎに関する不確定性
と、
測定の及ぼす撹乱に関する不確定性
は混同されてきたが、
特に後者については測定のしかたによっては正しくなく、
上記の不等式を下回る実験が可能であることが近年報告されている。
*3http://dx.doi.org/10.1103/Phys...
波動関数から理解する不確定性の意味 †
運動量の標準偏差がゼロであるような波動関数はどのようなものであろうか?
がエルミートであることを用いて式変形すれば、
&math( \sigma_p^2 &=\iiint\psi^*\left(\hat p-\langle p\rangle\right)^2\psi\,d\bm r\\ &=\iiint\left(\hat p\psi-\langle p\rangle\psi\right)^*
\left(\hat p\psi-\langle p\rangle\psi\right)\,d\bm r\\
&=\iiint\left|\hat p\psi-\langle p\rangle\psi\right|^2\,d\bm r\\ &=0 );
となり、すなわち至る所で
が要求される。これは、
を表わしており、このとき となり 波動関数の絶対値は によらず一定値を取る。すなわち波動関数は の全範囲に広がってしまう。
エーレンフェストの定理 †
初期状態において電子の存在確率があまり広がっておらず、 その広がりに対してポテンシャル の変化が十分に緩やかであれば、 電子の運動は古典論から予想されるものと等しくなるはずである。 このことを確かめてみよう。
まず、電子の位置座標の時間変化を求める。
&math( \frac{d}{dt}\langle x\rangle &=\frac{d}{dt}\iiint \psi^*x\psi\,d\bm r\\ &=\iiint\psi^* x\frac{\PD\psi}{\PD t}+\frac{\PD\psi^*}{\PD t}x\psi\,d\bm r\\ );
シュレーディンガー方程式により を書き直して、
&math( \frac{d}{dt}\langle x\rangle &=\iiint \psi^*x\frac{1}{i\hbar}\Big(-\frac{\hbar^2}{2m}\nabla^2\psi+V\psi\Big)\,d\bm r\\ &+\iiint \frac{1}{-i\hbar}\Big(-\frac{\hbar^2}{2m}\nabla^2\psi^*+V\psi^*\Big)x\psi\,d\bm r\\ );
を含む項は互いに打ち消し合って、
&math( \frac{d}{dt}\langle x\rangle &=\frac{i\hbar}{2m}\iiint \psi^*x(\nabla^2\psi)-(\nabla^2\psi^*)x\psi\,d\bm r\\ );
ここで部分積分により、
&math( \iiint(\nabla^2\psi^*)x\psi\,d\bm r &=-\iiint (\bm \nabla\psi^*)\cdot\bm \nabla(x\psi)\,d\bm r
+\underbrace{\int_S(\bm \nabla\psi^*\cdot x\psi)\cdot\bm n\,dS}_{=0}\\
&=\iiint \psi^*\nabla^2(x\psi)\,d\bm r
+\underbrace{\int_S(\psi^*\bm\nabla(x\psi))\cdot\bm n\,dS}_{=0}\\
);
したがって、
&math( \frac{d}{dt}\langle x\rangle &=\frac{i\hbar}{2m}\iiint \psi^*[x(\nabla^2\psi)-\nabla^2(x\psi)]\,d\bm r\\ &=\frac{i\hbar}{2m}\iiint \psi^*\left(-2\frac{\PD}{\PD x}\right)\psi\,d\bm r\\ &=\frac{1}{m}\langle p_x\rangle );
を得る。ここで、
&math( \nabla^2(x\psi) &=\left(\frac{\PD^2}{\PD x^2}+\frac{\PD^2}{\PD y^2}+\frac{\PD^2}{\PD z^2}\right)(x\psi)\\ &=\frac{\PD\psi}{\PD x}+\frac{\PD\psi}{\PD x}+x\frac{\PD^2\psi}{\PD x^2}+x\frac{\PD^2\psi}{\PD y^2}+x\frac{\PD^2\psi}{\PD z^2}\\ &=\left(2\frac{\PD}{\PD x}+x\nabla^2\right)\psi );
を用いた。一方、運動量の時間変化は、
&math( \frac{d}{dt}\langle p_x\rangle &=\frac{d}{dt}\iiint\psi^*\frac{\hbar}{i}\frac{\PD}{\PD x}\psi\,d\bm r\\ &=\frac{\hbar}{i}\iiint\psi^*\frac{\PD}{\PD x}\frac{\PD}{\PD t}\psi+\left(\frac{\PD}{\PD t}\psi^*\right)\frac{\PD}{\PD x}\psi\,d\bm r\\ &=\frac{\hbar}{i}\iiint\psi^*\frac{\PD}{\PD x}\frac{1}{i\hbar}\left(-\frac{\hbar^2}{2m}\nabla^2\psi+V\psi\right)\,d\bm r
- \frac{\hbar}{i}\iiint\frac{1}{-i\hbar}\left(-\frac{\hbar^2}{2m}\nabla^2\psi^*+V\psi^*\right)\frac{\PD}{\PD x}\psi\,d\bm r\\ );
ここで、
&math( \iiint\psi^*\frac{\PD}{\PD x}\nabla^2\psi\,d\bm r &=\iiint\psi^*\nabla^2\frac{\PD\psi}{\PD x}\,d\bm r\\ &=-\iiint\bm\nabla\psi^*\cdot\bm\nabla\frac{\PD\psi}{\PD x}\,d\bm r
- \underbrace{\int_S\left(\psi^*\bm\nabla\frac{\PD\psi}{\PD x}\right)\cdot\bm n\,dS}_{=0}\\ &=\iiint(\nabla^2\psi^*)\frac{\PD\psi}{\PD x}\,d\bm r
- \underbrace{\int_S\left(\bm\nabla\psi^*\cdot\frac{\PD\psi}{\PD x}\right)\cdot\bm n\,dS}_{=0}\\ &=\iiint(\nabla^2\psi^*)\frac{\PD\psi}{\PD x}\,d\bm r );
より を含む項は打ち消し合って、
&math( \frac{d}{dt}\langle p_x\rangle &=-\iiint\psi^*\left(\frac{\PD}{\PD x}(V\psi)-V\frac{\PD}{\PD x}\psi\right)\,d\bm r\\ &=-\iiint\psi^*\frac{\PD V}{\PD x}\psi\,d\bm r\\ &=-\left\langle\frac{\PD V}{\PD x}\right\rangle );
となり、 の期待値が古典論の運動方程式
を満たすことが示された。
巨視的極限に於いてシュレーディンガー方程式が古典論の運動方程式を与えるという この定理をエーレンフェストの定理と呼ぶ。
メモ †
上記干渉のアニメーションを求めるための Mathematica コード:
LANG:mathematica
anim = Table[
Plot3D[
Re[ Exp[I(Sqrt[(x - d)^2 + y^2] - t)]/((x - d)^2 + y^2) +
Exp[I(Sqrt[(x + d)^2 + y^2] - t)]/((x + d)^2 + y^2) ] /. d -> 20.25,
{x, -30, 30}, {y, 0, 60},
Mesh -> None, Mesh -> Automatic, ViewPoint -> 1.4 {1.2, 1, 1},
PlotPoints -> 401, ImageSize -> Large,
PlotRange -> {{-30, 30}, {0, 60}, {-0.01, 0.01}}
], {t, 0, 2 Pi, 2 Pi/40}
];
Export["double-slit.gif", anim, "GIF"]
2015-02-23 時点において、この計算にはかなりの時間(10分単位)がかかる。
質問・コメント †
*1 歴史的にはこの解釈がなされた時点で上記のような顕著な実験結果は得られておらず、この解釈が受け入れられるまでにはかなりの紆余曲折があった
*2 ピンと来なければ電磁気学で学んだ電荷の保存則の部分を復習せよ
*3 http://dx.doi.org/10.1103/PhysRevA.67.042105