基底の変換 †
異なる基底に対する表現 †
に2つの基底
を取ると、1つのベクトル
に対して2つの表現
が得られる。
以下では、
と
との間に成り立つ関係について考える。
基底の変換行列 †
上の
次元線形空間
に2つの基底を取る
これらの基底に対するベクトル
の表現
は、
(1)
(2)
の関係を満たす。図に表わせば、
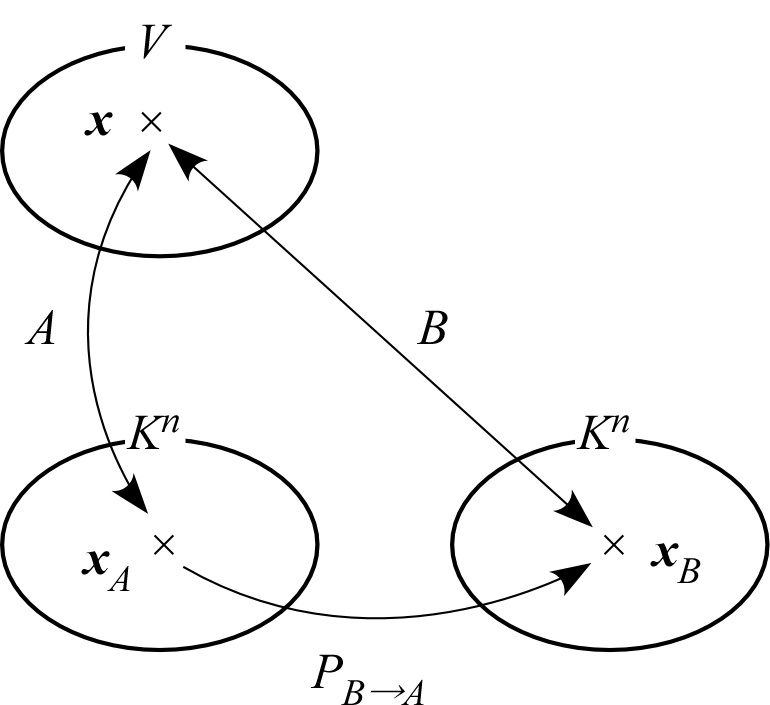
および
はともに
線形写像(同型写像)となるから、その合成写像
も線形写像(同型写像)である。
数ベクトルの線形写像は行列のかけ算で表せる †
一般に、数ベクトルから数ベクトルへの線形写像
は
行列のかけ算の形で表せる。
なぜなら、
とすると、
が線形写像であることから、
そこで、 †
ある
次正方行列
を用いて、
(3)
と表せる。
このとき、
を
基底
から 基底
への基底の変換行列と呼ぶ。
変換の向き †
上記を良く読んで「変換の向きは逆じゃないの?」と思うのは正しい感覚。
どうしてこの向きかというと、
(2) に (3) を代入して、
と (1) とを比べると、
(4)
となり、
は基底
を基底
に変換する。
数ベクトル表現を変換する (3) と、基底を変換する (4) とをしっかり区別して覚えよう。
具体例 †
上記の例であれば
と置いて、
すなわち、
したがって、
上の例で言えば、
であり、確かに成り立っている。
$P_{B\to A}$ の求め方 †
基底
の
番目の基底ベクトル
の
に対する表現
を考えるとわかりやすい。
なので(ただし
は
番目の基本ベクトル)、
と置けば、
したがって、
となって、
は
基底
の基底ベクトルの基底
に対する表現を並べて作った行列となる。
上の例ならば、
となって、確かに正しい。
正則性 †
当然、逆写像も線形写像であるから、
であり、
の関係がある。すなわち、基底の変換行列は正則行列である。
に、2つの基底を取る。
を
で展開すれば、
→
→
2つの式をまとめると、
この表式を用いて、
すなわち、
演習 †
に2つの基底
と
を取る。
(1)
から
への変換行列
、
から
への変換行列
を求めよ。
(2)
に対応する
を求めよ。
(3)
に対応する
を求めよ。
解答 †
(1)
より、
また、
より、
あるいは、
から求めても良い。
(2)
検算:
(3)
前の単元 <<<
線形代数II
>>> 次の単元
