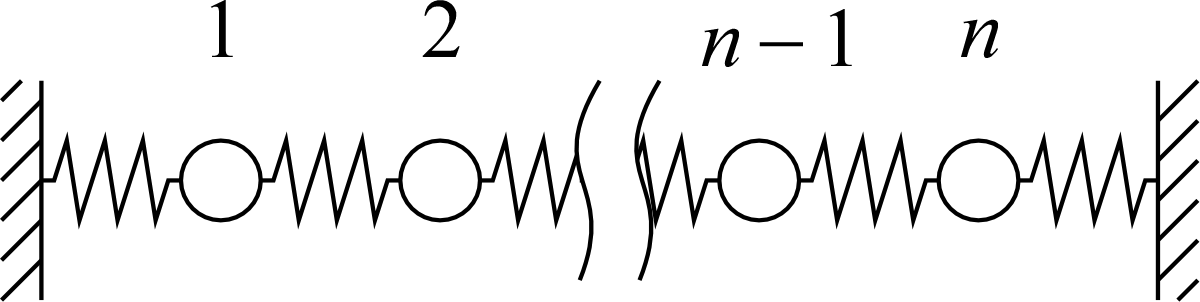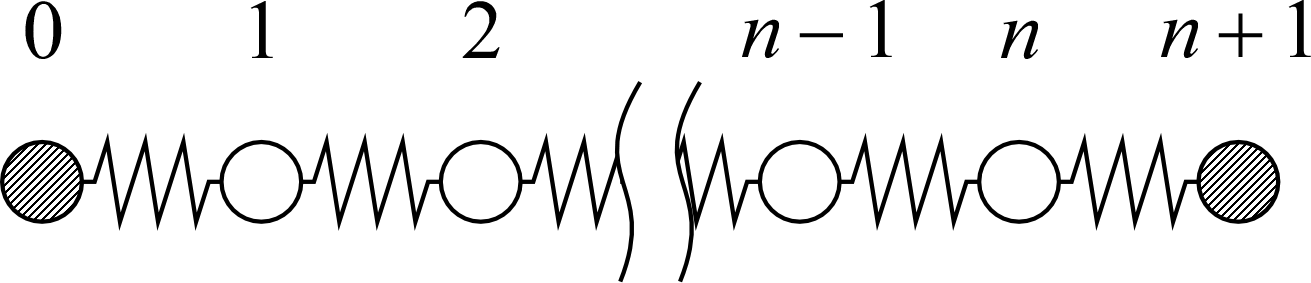線形代数II/連立線形微分方程式
概要 †
行列の対角化や行列の関数を利用して、連立線形微分方程式を解く。
1階線形微分方程式 †
基本 †
通常の1階線形微分方程式
$$\frac{dx(t)}{dt}=ax(t)$$
を解くには、まず両辺を $x(t)$ で割り、
$$\frac{\ \frac{dx(t)}{dt}\ }{x(t)}=\frac{d}{dt}\log x(t)=a$$
中辺、右辺を積分して($C'$: 積分定数)、指数関数を取ることにより
$$\log x(t)=at + C'$$
$$x(t)=Ce^{at}$$
とすればよい。ここで $C=e^{C'}$ であるが、$t=0$ を代入すれば
$$x(0)=C$$
となることに注意すると、
$$x(t)=e^{at}\,x(0)$$
と表すことができる。
連立方程式 †
未知の関数 $x_1(t),x_2(t)$ に対して 以下の連立1階線形微分方程式が与えられているとする。
$$\left\{ \begin{matrix} \displaystyle\frac{dx_1(t)}{dt}=\dot x_1(t)=ax_1(t)+bx_2(t) \\ \displaystyle\frac{dx_2(t)}{dt}=\dot x_2(t)=cx_1(t)+dx_2(t) \end{matrix} \right.$$
この方程式は
$$\bm x(t)=\begin{pmatrix}x_1(t)\\x_2(t)\end{pmatrix}, \ \ A=\begin{pmatrix}a&b\\c&d\end{pmatrix}$$
を用いれば
$$\frac{d\bm x(t)}{dt}=\dot{\bm x}(t)=A\bm x(t)$$
と表せるから、行列の関数を用いることで方程式の解を
$$ \bm x(t)=e^{At}\bm x(0) $$
として求められる!!!(ドヤッ
で終わってしまっても良いのだけれど念のため、$A$ が対角化可能な場合について行列の関数を用いない方法との対比を確認しておこう。
$A$ を $P^{-1}AP=D=\begin{pmatrix}\lambda_1&\\&\lambda_2\end{pmatrix}$ の形で対角化できるなら、1年生の二次形式のところでやったのと同様に、
$$ \bm x(t)=P\bm y(t)=P\begin{pmatrix}y_1(t)\\y_2(t)\end{pmatrix} $$
を満たす $\bm y(t)$ へと変数変換することで、
$$ \dot{\bm x}(t)=\frac{d}{dt}\{P\bm y(t)\}=P\dot{\bm y}(t)=A\bm x(t)=AP\bm y(t) $$
すなわち、
$$\dot{\bm y}(t)=P^{-1}AP\bm y(t)=D\bm y(t)$$
のように非対角項がゼロとなる方程式が得られる。これは
$$\left\{\begin{matrix} \dot y_1(t)=\lambda_1y_1(t)\\ \dot y_2(t)=\lambda_2y_2(t) \end{matrix} \right.$$
を表わすから、それぞれ $y_1(t),y_2(t)$ に対して独立に解くことができて、
$$\left\{\begin{matrix} y_1(t)=y_1(0)e^{\lambda_1t}\\ y_2(t)=y_2(0)e^{\lambda_2t}\end{matrix} \right.$$
あるいは $$\bm y(t)=\begin{pmatrix}e^{\lambda_1t}\\&e^{\lambda_2t}\end{pmatrix}\bm y(0)$$
のように解が得られる。
このように、方程式を単純化する基底を取って解を表わした座標を「基準座標」と呼ぶ。
最終的な問題は基準座標に対する解 $\bm y(t)$ を得ることではなく、 $\bm x(t)$ を求めることなので、 $\bm y(0)=P^{-1}\bm x(0)$ を使って変形すると、
$$\bm x(t)=P\bm y(t) =P\begin{pmatrix}e^{\lambda_1t}\\&e^{\lambda_2t}\end{pmatrix}\bm y(0) =P\begin{pmatrix}e^{\lambda_1t}\\&e^{\lambda_2t}\end{pmatrix}P^{-1}\bm x(0) $$
が得られ、これが初期条件 $\bm x(0)$ が与えられた際に $\bm x(t)$ を求めるための式となる。
先にやったように $e^{At}=P\begin{pmatrix}e^{\lambda_1t}\\&e^{\lambda_2t}\end{pmatrix}P^{-1}$ であることを用いてこの式を、
$$\bm x(t)=e^{At}\bm x(0)$$
と書き直すと、通常の線形微分方程式の解とほとんど同じに解ける、というわけだ。
$$ \begin{array}{lll} \dot x(t)=ax(t) &\to& x(t)=x(0)e^{at} \\ \dot{\bm x}(t)=A\bm x(t) &\to& \bm x(t)=e^{At}\,\bm x(0) \\ \end{array} $$
またこの $\bm x(t)$ が与えられた微分方程式を満たすことも容易に確認できる。
$$\dot{\bm x}(t)=\frac{d}{dt}\left\{e^{At}\bm x(0)\right\} =\left\{\frac{d}{dt}e^{At}\right\}\bm x(0) =Ae^{At}\bm x(0) =A\bm x(t) $$
$A$ が対角化可能でない場合にも $\bm x(t)=e^{At}\bm x(0)$ と書いて問題ないが、 $e^{At}$ を固有値を用いてどのように書いたらよいるかを理解するには 発展:ジョルダン標準形 について学ぶ必要がある。(加えて、固有値にゼロを含むときも特別扱いが必要になる)
例題 †
$\left\{\begin{matrix} \frac{dx_1(t)}{dt}&=3x_1(t)+\phantom 3x_2(t)\\[3mm] \frac{dx_2(t)}{dt}&=\phantom 3x_1(t)+3x_2(t) \end{matrix}\right.$ を初期条件 $x_1(0)=6,x_2(0)=2$ の下で解け。
$\bm x(t)=\begin{pmatrix}x_1(t)\\x_2(t)\end{pmatrix}$、 $A=\begin{pmatrix}3&1\\1&3\end{pmatrix}$ と置けば、 $\dot{\bm x}(t)=A\bm x(t)$ と書けるから、
$\bm x(t)=e^{tA}\bm x(0)$ と表せる。
$P^{-1}AP=\begin{pmatrix}\lambda_1\\&\lambda_2\end{pmatrix}$ と対角化できるならさらに変形して、
$$\bm x(t)=P\begin{pmatrix}e^{\lambda_1t}\\&e^{\lambda_2t}\end{pmatrix}P^{-1}\bm x(0)$$
である($\lambda_1\ne 0,\lambda_2\ne 0$ の時)。
$A$ の固有値を求め、対角化しよう。
$$|A-\lambda E|=\begin{vmatrix}3-\lambda&1\\1&3-\lambda\end{vmatrix}=(3-\lambda)^2-1=(4-\lambda)(2-\lambda)$$
より、$\lambda_1=4,\lambda_2=2$
それぞれに対応する固有ベクトルは、
$(A-4 E)\bm x=\begin{pmatrix}-1&1\\1&-1\end{pmatrix}\bm x=\bm 0$ より $\bm x=s\begin{pmatrix}1\\1\end{pmatrix}$
$(A-2 E)\bm x=\begin{pmatrix}1&1\\1&1\end{pmatrix}\bm x=\bm 0$ より $\bm x=s\begin{pmatrix}1\\-1\end{pmatrix}$
したがって、$P=\begin{pmatrix}1&1\\1&-1\end{pmatrix}$、$P^{-1}=\frac{1}{2}\begin{pmatrix}1&1\\1&-1\end{pmatrix}$、$P^{-1}AP=\begin{pmatrix}4\\&2\end{pmatrix}$ となって、
$$\begin{aligned} \bm x(t)&=\begin{pmatrix}1&1\\1&-1\end{pmatrix}\begin{pmatrix}e^{4t}\\&e^{2t}\end{pmatrix}\frac{1}{2}\begin{pmatrix}1&1\\1&-1\end{pmatrix}\begin{pmatrix}6\\2\end{pmatrix}\\ &=\begin{pmatrix}e^{4t}&e^{2t}\\e^{4t}&-e^{2t}\end{pmatrix}\begin{pmatrix}1&1\\1&-1\end{pmatrix}\begin{pmatrix}3\\1\end{pmatrix}\\ &=\begin{pmatrix}e^{4t}&e^{2t}\\e^{4t}&-e^{2t}\end{pmatrix}\begin{pmatrix}4\\2\end{pmatrix}\\ &=\begin{pmatrix}4e^{4t}+2e^{2t}\\4e^{4t}-2e^{2t}\end{pmatrix}\\ \end{aligned}$$
が求める解である。
検算 †
上記の $\bm x(t)$ より
$$\bm x(0)=\begin{pmatrix}6\\2\end{pmatrix}$$
および、
$$\dot{\bm x}(t)=\begin{pmatrix}16e^{4t}+4e^{2t}\\16e^{4t}-4e^{2t}\end{pmatrix}\\$$
$$A\bm x(t)=\begin{pmatrix}3&1\\1&3\end{pmatrix}\begin{pmatrix}4e^{4t}+2e^{2t}\\4e^{4t}-2e^{2t}\end{pmatrix}=\begin{pmatrix}16e^{4t}+4e^{2t}\\16e^{4t}-4e^{2t}\end{pmatrix}\\$$
を確かめられる。
演習問題 †
以下の微分方程式を境界条件 $x_1(0)=1,x_2(0)=2$ の下で解け。
$$ \begin{cases} \frac{d}{dt}x_1(t)=-x_1(t)+x_2(t)\\ \frac{d}{dt}x_2(t)=\phantom{-}x_1(t)-x_2(t)\\ \end{cases} $$
2階線形微分方程式 †
基本 †
通常の2階線形微分方程式が次のように与えられたとする。
$$\frac{d^2x(t)}{dt^2}=-\omega^2x(t)\hspace{10mm}(\omega>0)$$
$$x''=-\omega^2x$$
これを解くには*1参考:http://w3e.kanazawa-it.ac.jp/m...、 まず全体に $x'$ をかけてから積分して、
$$x'x''+\omega^2xx'=0$$
$$\frac12x'^2+\frac12\omega^2x^2=C_0\hspace{1cm}C_0:\text{ 積分定数}$$
を得る(この関係は物理学ではエネルギー保存則と関係が深い)。
$x$ が実数関数であれば明らかに $C_0\ge 0$ であるから $2C_0=\omega^2A^2\ge 0$ と書くことにすると、
$$x'^2=\omega^2A^2-\omega^2x^2$$
すなわち、
$$x'=\pm\omega\sqrt{A^2-x^2}$$
を得る(三角関数の形が見えてきた)。 変数分離して両辺を積分すると、
$$\pm\frac{x'}{\sqrt{A^2-x^2}}=\omega$$
$$\pm\int \frac{x'}{\sqrt{A^2-x^2}}dt=\pm\int \frac{dx}{\sqrt{A^2-x^2}}=\pm\cos^{-1}\frac xA=\omega t+\theta\hspace{1cm}\theta:\text{ 積分定数}$$
両辺の $\cos$ を取ると $\cos x=\cos(-x)$ より $\pm$ は消えて、
$$ x(t)=A\cos(\omega t+\theta)=C\cos\omega t+C'\sin\omega t $$
ただし、$C=A\cos\theta,C'=-A\sin\theta$ と表せる。
$$\dot x(t)=-\omega C\sin\omega t+\omega C'\cos\omega t$$
より、
$$x(0)=C, \dot x(0)=\omega C'$$
であるから $t=0$ における境界条件を用いれば
$$x(t)=x(0)\cos\omega t+\frac{\dot x(0)}{\omega}\sin\omega t$$
と表せる。
連立方程式 †
未知の関数 $x_1(t),x_2(t)$ が次の2階線形連立微分方程式を満たす時、
$$\left\{ \begin{matrix} \displaystyle\frac{d^2x_1(t)}{dt^2}=\ddot x_1(t)=-ax_1(t)-bx_2(t) \\ \displaystyle\frac{d^2x_2(t)}{dt^2}=\ddot x_2(t)=-cx_1(t)-dx_2(t) \end{matrix} \right.$$
この方程式はベクトル関数 $\bm x(t)=\begin{pmatrix}x_1(t)\\x_2(t)\end{pmatrix}$、 行列 $A=\begin{pmatrix}a&b\\c&d\end{pmatrix}$ を用いて、
$$\frac{d^2\bm x(t)}{dt^2}=\ddot{\bm x}(t)=-A\bm x(t)$$
と表せる。
もし $A$ を $P^{-1}AP=D=\begin{pmatrix}\lambda_1&\\&\lambda_2\end{pmatrix}$ の形で対角化できるなら、
$$ \bm x(t)=P\bm y(t)=P\begin{pmatrix}y_1(t)\\y_2(t)\end{pmatrix} $$
の変数変換により一次の時と同様に、
$$\ddot{\bm y}(t)=-P^{-1}AP\bm y(t)=-D\bm y(t)$$
が得られる。
$\lambda_1>0,\ \lambda_2>0$ であれば $\omega_1=\sqrt{\lambda_1},\ \omega_2=\sqrt{\lambda_2}$ と置けて、これは
$$\left\{\begin{matrix} \ddot y_1(t)=-\lambda_1y_1(t)=-\omega_1^2y_1(t)\\ \ddot y_2(t)=-\lambda_2y_2(t)=-\omega_2^2y_2(t) \end{matrix} \right.$$
という方程式を表わすから、その解を
$$\left\{\begin{matrix} y_1(t)=y_1(0)\cos\omega_1t+\frac{\dot y_1(0)}{\omega_1}\sin\omega_1t\\ y_2(t)=y_2(0)\cos\omega_2t+\frac{\dot y_2(0)}{\omega_2}\sin\omega_2t \end{matrix}\right.$$
あるいは
$$\bm y(t)=\begin{pmatrix}\cos\omega_1t\\&\cos\omega_2t\end{pmatrix}\bm y(0)+ \begin{pmatrix}\frac{\sin\omega_1t}{\omega_1}\\&\frac{\sin\omega_1t}{\omega_1}\end{pmatrix}\dot{\bm y}(0)$$
と表せる。$\bm y(0)=P^{-1}\bm x(0), \dot{\bm y}(0)=P^{-1}\dot{\bm x}(0)$ を用いて書き直すと、
$$\bm x(t)=P\bm y(t)=P\begin{pmatrix}\cos\omega_1t\\&\cos\omega_2t\end{pmatrix}P^{-1}\bm x(0)+ P\begin{pmatrix}\frac{\sin\omega_1t}{\omega_1}\\&\frac{\sin\omega_1t}{\omega_1}\end{pmatrix}P^{-1}\dot{\bm x}(0)$$
これが、初期条件 $\bm x(0),\dot{\bm x}(0)$ が与えられた際に $\bm x(t)$ を求める式になる。
$\omega=\sqrt\lambda$ であったことを念頭に置きつつ「行列の関数」をイメージすれば、
$$\bm x(t)=\Bigg[\cos\left(\sqrt{A}\,t\right)\Bigg]\bm x(0)+\Bigg[\frac{\sin\left(\sqrt{A}\,t\right)}{\sqrt{A}}\Bigg]\dot{\bm x}(0)$$
の形であり、通常の調和振動の式
$$x(t)=x(0)\cos\omega t+\frac{\dot x(0)}{\omega}\sin\omega t$$
との類似性が際立つ。
ここで表れた $\sqrt A$ を含む「行列の関数」は先の授業でやったような「固有値の整数次のみの多項式」の形では表せないが、多項式が分数次の項を含んでも良いとして定義を拡張すれば、ほぼ同じ議論でこの書き方を正当化できる。
例題 †
次の連立微分方程式を考える。
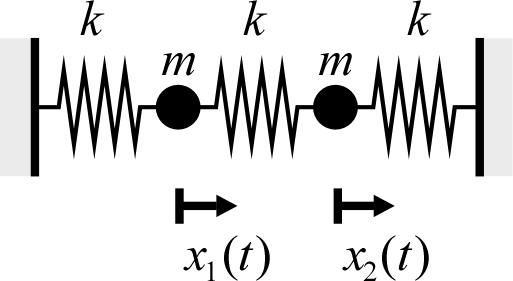
$$\left\{\begin{matrix} m\ddot x_1(t)=-kx_1(t)-k\{x_1(t)-x_2(t)\}\\ m\ddot x_2(t)=-kx_2(t)-k\{x_2(t)-x_1(t)\}\\ \end{matrix}\right.$$
これは右図のように、3つのバネで繋がれた2つの質点の運動を記述する方程式を考えているのであるが、 物理モデルから上記方程式を組み立てる部分は数学の範疇ではないので、線形代数学においては 上記方程式をどのように解くかに焦点を絞る。
$\bm x(t)=\begin{pmatrix}x_1(t)\\x_2(t)\end{pmatrix}$、 $\displaystyle A=\frac{k}{m}\begin{pmatrix}2&-1\\-1&2\end{pmatrix}$ と置けば、上式は
$$\ddot{\bm x}(t)=-A\bm x(t)$$
と書けるから、$A$ の固有値がすべて正であるとき、その解を形式的に
$$\bm x(t)=\Bigg[\cos\sqrt{A}t\Bigg]\bm x(0)+\Bigg[\frac{\sin\sqrt{A}t}{\sqrt A}\Bigg]\dot{\bm x}(t)$$
と書ける。
今の場合、$|(m/k)A-\lambda' E|=\begin{vmatrix}2-\lambda'&-1\\-1&2-\lambda'\end{vmatrix}=(2-\lambda')^2-1=(1-\lambda')(3-\lambda')=0$ より、
$\lambda'=1,3$ すなわち $\lambda_1=\frac{k}{m}>0,\lambda_2=\frac{3k}{m}>0$ であり、
対応する固有ベクトルはそれぞれ $\begin{pmatrix}1\\1\end{pmatrix},\begin{pmatrix}1\\-1\end{pmatrix}$ であるから、
$P=\begin{pmatrix}1&1\\1&-1\end{pmatrix}$ と置けば、
$$P^{-1}AP=\begin{pmatrix}\lambda_1&0\\0&\lambda_2\end{pmatrix}$$
として対角化できる。
このとき、
$$\bm x(t)= P\begin{pmatrix}\cos\sqrt{\lambda_1}t&0\\0&\cos\sqrt{\lambda_2}t\end{pmatrix}P^{-1}\bm x(0)+ P\begin{pmatrix}\frac{\sin\sqrt{\lambda_1}t}{\sqrt{\lambda_1}}&0\\0&\frac{\sin\sqrt{\lambda_2}t}{\sqrt{\lambda_2}}\end{pmatrix}P^{-1}\dot{\bm x}(0)$$
と表せ、
$$ \begin{aligned} P\begin{pmatrix}a\\&b\end{pmatrix}P^{-1}&=\begin{pmatrix}1&1\\1&-1\end{pmatrix}\begin{pmatrix}a\\ &b\end{pmatrix}\frac{1}{2}\begin{pmatrix}1&1\\1&-1\end{pmatrix}\\ &=\frac{1}{2}\begin{pmatrix}a&b\\a&-b\end{pmatrix}\begin{pmatrix}1&1\\1&-1\end{pmatrix}\\ &=\frac{1}{2}\begin{pmatrix}a+b&a-b\\a-b&a+b\end{pmatrix} \end{aligned} $$
を用いて計算を進めると、
$$ \bm x(t)= \frac{1}{2}\begin{pmatrix} \cos{\omega_1}t+\cos{\omega_2}t&\cos{\omega_1}t-\cos{\omega_2}t\\ \cos{\omega_1}t-\cos{\omega_2}t&\cos{\omega_1}t+\cos{\omega_2}t \end{pmatrix}\bm x(0)+ \frac{1}{2\omega_1}\begin{pmatrix} \sin{\omega_1}t+\tfrac1{\sqrt3}\sin{\omega_2}t& \sin{\omega_1}t-\tfrac1{\sqrt3}\sin{\omega_2}t\\ \sin{\omega_1}t-\tfrac1{\sqrt3}\sin{\omega_2}t& \sin{\omega_1}t+\tfrac1{\sqrt3}\sin{\omega_2}t\\ \end{pmatrix}\dot{\bm x}(0) $$
が $\bm x(0),\dot{\bm x}(0)$ で表わした $\bm x(t)$ の表式となる。 ここで、$\omega_1=\sqrt{\lambda_1}=\sqrt{\frac{k}{m}},\omega_2=\sqrt{\lambda_2}=\sqrt3\omega_1$ である。
物理的意味 †
計算途中で表れた $y_1(t),y_2(t)$ は物理的にどんな意味を持つだろうか?
これらはそれぞれ個別に調和振動子の方程式
$$ \begin{cases} \ddot y_1=-\omega_1^2y_1\\ \ddot y_2=-\omega_2^2y_2\\ \end{cases} $$
を見たし、$\bm x(t)=P\bm y(t)=\begin{pmatrix}1&1\\1&-1\end{pmatrix}\begin{pmatrix}y_1(t)\\y_2(t)\end{pmatrix}$ の関係があった。この $\bm x(t)$ を
$$ \bm x(t)=\begin{pmatrix}1\\1\end{pmatrix}\underbrace{A_1\cos(\omega_1 t+\theta_1)}_{y_1(t)} +\begin{pmatrix}1\\-1\end{pmatrix}\underbrace{A_2\cos(\omega_2 t+\theta_2)}_{y_2(t)} $$
と書きなおすと分かるように、
それぞれ表す。
逆位相モードでは3つのバネがすべて働くのに対して、
同位相モードでは真ん中のバネが働かないため、
逆位相モードの振動数は同位相モードよりも $\sqrt3$ 倍だけ大きくなっている。
この系の任意の運動を、この2つの振動モードの重ね合わせとして表せる、 というのが $\bm x(t)=P\bm y(t)$ の変換の意味である。
解析力学的な話をするならば、$\bm x$ と $\bm y$ との間は双方向に変数変換可能であるから、 $\bm x$ の代りに $\bm y$ を独立変数と取ることができて、このとき2つの質点の連成振動の系は 2つの独立な調和振動子の系に変換可能であると言える。
これは非常に重要な変換で、例えば固体物理で扱う複雑に振動する格子振動を無数の調和振動子に変数変換した際の、それぞれの振動モードの振幅が量子化したものがフォノンであったり、真空中の電磁場をやはり無数の調和振動子に変数変換した際の、それぞれの振動モードの振幅が量子化したものがフォトン(光子)だったりといったように、応用範囲も広いものである。
演習問題 †
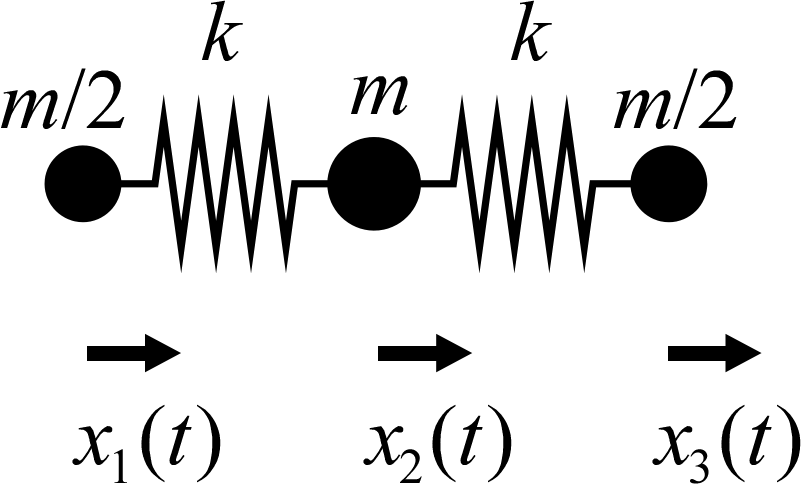
$x$ 軸上のみを動ける3つの質点が、ばね定数 $k$ を持つ2つのばねで連結された図のような系を考える。ただし、真ん中の質点の質量を $m$、両端の質点の質量をそれぞれ $m/2$ とする。このとき運動方程式は次のようになる。以下の問いに従って、この方程式の一般解を基準運動に分離せよ。
$$ \begin{cases} (m/2)\ddot x_1(t)=\phantom{-}k\{x_2(t)-x_1(t)\}\\ \hspace{6.2mm}m\ddot x_2(t)=-k\{x_2(t)-x_1(t)\}+k\{x_3(t)-x_2(t)\}\\ (m/2)\ddot x_3(t)=\phantom{-k\{x_2(t)-x_1(t)\}}-k\{x_3(t)-x_2(t)\}\\ \end{cases} $$
(1) $\bm x(t)=\begin{pmatrix}x_1(t)\\x_2(t)\\x_3(t)\end{pmatrix}$ に対して、与えられた方程式を $\ddot {\bm x}=-A\bm x$ と表した際の係数行列 $A$ を求めよ。
(2) $A$ の固有値 $\lambda_1,\lambda_2,\lambda_3$ を求めよ。また、対応する固有ベクトルを1つずつ求め $\bm p_1,\bm p_2,\bm p_3$ とせよ。ただし、$\lambda_1<\lambda_2<\lambda_3$ とする。
(3) $P=\Big(\bm p_1\ \bm p_2\ \bm p_3\Big)$ に対して $P^{-1}$ を求めよ。
(4) $\bm y=\begin{pmatrix}y_1(t)\\y_2(t)\\y_3(t)\end{pmatrix}$ が $\bm x=P\bm y$ を満たすとき、 $y_1,y_2,y_3$ に対する運動方程式を求め、それぞれの一般解 $y_1^*,y_2^*,y_3^*$ を適当なパラメータを含む形で書き下せ。
(5) $\bm x$ の一般解は $\bm x(t)=\bm p_1y_1^*+\bm p_3y_3^*+\bm p_3y_3^*$ で与えられることを念頭に置き、 $y_1,y_2,y_3$ で表される基準運動がどのような運動を表すか説明せよ。
解答例 †
(1) $\bm x(t)=\begin{pmatrix}x_1(t)\\x_2(t)\\x_3(t)\end{pmatrix}$ に対して、与えられた方程式を $\ddot {\bm x}=-A\bm x$ と表した際の係数行列 $A$ を求めよ。
$$ \begin{cases} \ddot x_1=-\frac{2k}{m}x_1+\frac{2k}{m}x_2\\ \ddot x_2=+\frac{k}{m}x_1-\frac{2k}{m}x_2+\frac{k}{m}x_3\\ \ddot x_3=\phantom{+\frac kmx_1}+\frac {2k}mx_2-\frac {2k}mx_3\\ \end{cases} $$
であるから、
$$ A=\frac km\begin{pmatrix} 2&-2&0\\ {}-1&2&-1\\ 0&-2&2 \end{pmatrix} $$
(2) $A$ の固有値 $\lambda_1,\lambda_2,\lambda_3$ を求めよ。また、対応する固有ベクトルを1つずつ求め $\bm p_1,\bm p_2,\bm p_3$ とせよ。ただし、$\lambda_1<\lambda_2<\lambda_3$ とする。
$$ \begin{aligned} \big|\tfrac mkA-\lambda' I\big| &= \begin{vmatrix} 2-\lambda'&-2&0\\ {}-1&2-\lambda'&-1\\ 0&-2&2-\lambda' \end{vmatrix}=\begin{vmatrix} 2-\lambda'&0&-2+\lambda'\\ {}-1&2-\lambda'&-1\\ 0&-2&2-\lambda' \end{vmatrix}\\ &=(2-\lambda')\begin{vmatrix} 1&0&-1\\ {}-1&2-\lambda'&-1\\ 0&-2&2-\lambda' \end{vmatrix}=(2-\lambda')\begin{vmatrix} 1&0&0\\ {}-1&2-\lambda'&-2\\ 0&-2&2-\lambda' \end{vmatrix}\\ &=(2-\lambda')\begin{vmatrix} 2-\lambda'&-2\\ {}-2&2-\lambda' \end{vmatrix}=(2-\lambda')\begin{vmatrix} {}-\lambda'&-\lambda'\\ {}-2&2-\lambda' \end{vmatrix}\\ &=-\lambda'(2-\lambda')\begin{vmatrix} 1&1\\ {}-2&2-\lambda' \end{vmatrix}=-\lambda'(2-\lambda')\begin{vmatrix} 1&0\\ {}-2&4-\lambda' \end{vmatrix}\\ &=-\lambda'(2-\lambda')(4-\lambda')=0 \end{aligned} $$
より $\lambda'=0,2,4$ であるから $\lambda_1=0,\lambda_2=2m/k,\lambda_3=4m/k$ となる。
またこの時、
$$ \big(\tfrac mkA-0 I\big)\bm p_1=0 $$
の拡大係数行列を同値変形すれば、
$$ \begin{pmatrix} 2&-2&0\\ {}-1&2&-1\\ 0&-2&2 \end{pmatrix}\sim\begin{pmatrix} 1&-1&0\\ {}-1&2&-1\\ 0&-1&1 \end{pmatrix}\sim\begin{pmatrix} 1&-1&0\\ 0&1&-1\\ 0&-1&1 \end{pmatrix}\sim\begin{pmatrix} 1&0&-1\\ 0&1&-1\\ 0&0&0 \end{pmatrix} $$
そこで掃き出せなかった3列目に対応して $z=t$ と置いて $\bm p_1$ の一般解は
$$ \bm p_1=t\begin{pmatrix} 1\\1\\1 \end{pmatrix} $$
と求まる。こでは1つ求めればよいので例えば $\bm p_1=\begin{pmatrix}1\\1\\1\end{pmatrix}$ が答えになる。
$$ \big(\tfrac mkA-2 I\big)\bm p_2=0 $$
の拡大係数行列を同値変形すれば、
$$ \begin{pmatrix} 0&-2&0\\ {}-1&0&-1\\ 0&-2&0 \end{pmatrix}\sim\begin{pmatrix} 1&0&1\\ 0&1&0\\ 0&0&0 \end{pmatrix} $$
そこで掃き出せなかった3列目に対応して $z=t$ と置けば $\bm p_2$ の一般解は
$$ \bm p_2=t\begin{pmatrix} {}-1\\0\\1 \end{pmatrix} $$
と求まる。こでは1つ求めればよいので例えば $\bm p_2=\begin{pmatrix}-1\\0\\1\end{pmatrix}$ が答えになる。
$$ \big(\tfrac mkA-4 I\big)\bm p_3=0 $$
の拡大係数行列を同値変形すれば、
$$ \begin{pmatrix} {}-2&-2&0\\ {}-1&-2&-1\\ 0&-2&-2 \end{pmatrix}\sim\begin{pmatrix} 1&1&0\\ 1&2&1\\ 0&1&1 \end{pmatrix}\sim\begin{pmatrix} 1&1&0\\ 0&1&1\\ 0&1&1 \end{pmatrix}\sim\begin{pmatrix} 1&0&-1\\ 0&1&1\\ 0&0&0 \end{pmatrix} $$
そこで掃き出せなかった3列目に対応して $z=t$ と置けば $\bm p_3$ の一般解は
$$ \bm p_3=t\begin{pmatrix} 1\\-1\\1 \end{pmatrix} $$
と求まる。ここでは1つ求めればよいので例えば $\bm p_3=\begin{pmatrix}1\\-1\\1\end{pmatrix}$ が答えになる。
(3) $P=\Big(\bm p_1\ \bm p_2\ \bm p_3\Big)$ に対して $P^{-1}$ を求めよ。
$$ P=\begin{pmatrix} 1&-1&1\\ 1&0&-1\\ 1&1&1 \end{pmatrix} $$
であるから、
$$ \begin{aligned} \big(\,P\ I\,\big)&=\begin{pmatrix} 1&-1&1&1&0&0\\ 1&0&-1&0&1&0\\ 1&1&1&0&0&1 \end{pmatrix}\sim\begin{pmatrix} 1&-1&1&1&0&0\\ 0&1&-2&-1&1&0\\ 0&2&0&-1&0&1 \end{pmatrix}\sim\begin{pmatrix} 1&0&-1&0&1&0\\ 0&1&-2&-1&1&0\\ 0&0&4&1&-2&1 \end{pmatrix}\\ &\sim\begin{pmatrix} 4&0&-4&0&4&0\\ 0&2&-4&-2&2&0\\ 0&0&4&1&-2&1 \end{pmatrix}\sim\begin{pmatrix} 4&0&0&1&2&1\\ 0&2&0&-1&0&1\\ 0&0&4&1&-2&1 \end{pmatrix} \end{aligned} $$
したがって、
$$ P^{-1}=\frac14\begin{pmatrix} 1&2&1\\ {}-2&0&2\\ 1&-2&1 \end{pmatrix} $$
(4) $\bm y=\begin{pmatrix}y_1(t)\\y_2(t)\\y_3(t)\end{pmatrix}$ が $\bm x=P\bm y$ を満たすとき、 $y_1,y_2,y_3$ に対する運動方程式を求め、それぞれの一般解 $y_1^*,y_2^*,y_3^*$ を適当なパラメータを含む形で書き下せ。
$\ddot{\bm x}=-A\bm x$ に $\bm x=P\bm y$ を代入すれば、
$$ P\ddot{\bm y}=-AP\bm y $$
$$ \ddot{\bm y}=-P^{-1}AP\bm y=-\begin{pmatrix} 0\\ &\frac{2k}{m}\\ &&\frac{4k}{m} \end{pmatrix}\bm y $$
すなわち、$y_1,y_2,y_3$ に対する運動方程式は、
$$ \begin{cases} \ddot y_1(t)=0\\ \ddot y_2(t)=-\frac{2k}{m}y_2(t)\\ \ddot y_3(t)=-\frac{4k}{m}y_3(t)\\ \end{cases} $$
これらはすぐに解けて一般解は
$$ \begin{cases} \ddot y_1^*(t)=At+B\\ \ddot y_2^*(t)=C\cos(\sqrt{\frac{2k}{m}}\,t+D)\\ \ddot y_3^*(t)=E\cos(2\sqrt{\frac{k}{m}}\,t+F)\\ \end{cases} $$
(5) $\bm x$ の一般解は $\bm x(t)=\bm p_1y_1^*+\bm p_3y_3^*+\bm p_3y_3^*$ で与えられることを念頭に置き、 $y_1,y_2,y_3$ で表される基準運動がどのような運動を表すか説明せよ。
$\bm x$ の一般解は次のように表せる。
$$ \bm x(t)= \begin{pmatrix}1\\1\\1\end{pmatrix}\underbrace{(At+B)}_{y_1^*}+ \begin{pmatrix}-1\\0\\1\end{pmatrix}\underbrace{C\cos\Big(\sqrt{\frac{2k}{m}}\,t+D\Big)}_{y_2^*}+ \begin{pmatrix}1\\-1\\1\end{pmatrix}\underbrace{E\cos\Big(2\sqrt{\frac km}\,t+F\Big)}_{y_3^*} $$
$y_1^*$ の係数 $\begin{pmatrix}1\\1\\1\end{pmatrix}$ は3つの質点がすべて同じ速度で移動することを表しており、すなわち $y_1^*$ は平行移動に対応する運動である。しがって、このモードは等速直線運動になっている($At+B$)。
$y_2^*$ の係数 $\begin{pmatrix}-1\\0\\1\end{pmatrix}$ は中央の質点が静止したまま両側の質点が中央の質点に対して対称に運動するモードに対応する。質量 $m/2$ がばね定数 $k$ を感じて振動するため振動数は $\sqrt{\frac{2k}m}$ となる。
$y_2^*$ の係数 $\begin{pmatrix}1\\-1\\1\end{pmatrix}$ は中央の質点と、両側の質点とが逆向きに同じ振幅で運動するモードに対応する。両端の重りに対してはばね定数 $k$ のバネが質量 $m/2$ の移動量の2倍伸び縮みし、中央の重りに対してはばね定数 $k$ のばね2本が移動量の2倍伸び縮みするため、どちらも角振動数は同じ値 $2\sqrt{\frac{k}m}$ を取る。
発展:$n$ 粒子の系 †
両端を壁で挟まれた2つの重りと3つのバネの系を上で見たが、
これを一般化して $n$ 個の重りの系を考える。
重りは水平にのみ運動可能で、時刻 $t$ における $j$ 番目の重りのつり合いの位置からの変位を $x_j(t)$ とする。
重りの質量 $M$、バネのバネ定数 $K$ はすべて等しいとする。
これは固体物理における格子振動のモデルと関係が深く、しっかり理解する価値のある問題である。 その場合、$n$ はアボガドロ数(1次元なので)の三乗根に匹敵するような大きな値となりうる。
$j$ 番目の重りの運動方程式 †
個々の重りはそこに直接つながる左右のばねから力を受ける。さしあたり両端を無視すれば、$j$ 番目の重りの左右のバネの伸びは $x_j-x_{j-1}$ と $x_{j+1}-x_j$ であるから、
$$ \begin{aligned} M\ddot x_k &=-K\big[(x_j-x_{j-1})-(x_{j+1}-x_j)\big]\\ \ddot x_k&=-\frac KM(-x_{j-1}+2x_j-x_{j+1}) \end{aligned} $$
が運動方程式となる。
左辺が時間に対する2階微分なのに対して、
右辺は $j$ に対する2階「差分」になっていることに注意せよ。
$j$ に対する差分:
$$\Delta x_j=x_j-x_{j-1}$$
$j$ に対する差分の差分 = 2階差分:
$$\Delta x_{j+1}-\Delta x_j=x_{j+1}-2x_j+x_{j-1}$$
動かない粒子を追加する †
$j=1,n$ については壁側に粒子がないため
$$ \ddot x_1=-\frac KM(\underbrace{\phantom{-x_{j-1}}}_{x_0\,\text{はない}}+2x_1-x_2) $$ $$ \ddot x_n=-\frac KM(-x_{n-1}+2x_n\underbrace{\phantom{-x_{j+1}}}_{x_{n+1}\,\text{はない}}) $$
のように他と異なる方程式になってしまい見通しが悪い。そこで壁の代わりに $j=0,n+1$ に固定された重りがあると考えよう。
すると $j=1,n$ についても他の粒子と同様に
$$ \ddot x_1=-\frac KM(-x_0+2x_1-x_2) $$
$$ \ddot x_n=-\frac KM(-x_{n-1}+2x_n-x_{n+1}) $$
と書くことができて、統一的に扱えるようになる。(もともと $x_j$ はつり合いの位置からの変位なので、$x_0=x_{n+1}=0$ に固定すればこれらの項はあってもなくても同じなのだ)
解くべき方程式 †
結果として得られる方程式は、
$\bm x(t)=\begin{pmatrix}x_1(t)\\x_2(t)\\\vdots\\x_n(t)\end{pmatrix}$、 $\displaystyle A=\frac{k}{m}\begin{pmatrix}2&-1\\-1&2&-1\\&\ddots&\ddots&\ddots\\&&-1&2&-1\\&&&-1&2\end{pmatrix}$
に対して、
$$ \ddot {\bm x}(t)=-A\bm x(t)\tag{*} $$
であるが、両端に仮想粒子を加えれば
$\bm x'(t)=\begin{pmatrix}0\\\hdashline x_1(t)\\x_2(t)\\\vdots\\x_n(t)\\\hdashline 0\end{pmatrix}$、 $\displaystyle A'=\frac{k}{m}\left(\begin{array}{c:ccc:c}0&0&&&\\\hdashline-1&2&-1&\\&\ddots&\ddots&\ddots&\\&&-1&2&-1\\\hdashline&&&0&0\end{array}\right)$
に対して、
$$ {\ddot {\bm x}}'(t)=-A'\bm x'(t) $$
と書くこともでき、この形では $j=1,\dots,n$ に対して $x_j$ の運動方程式はすべて同じ形、つまり $j$ に対する二階差分になる。
$n+2$ 次の $\ddot{\bm x}'=A'\bm x'$ から破線で区切られた $n$ 次の部分を取り出したのが $\ddot{\bm x}=A\bm x$ である。
同時固有関数となる特殊解 †
式 $(*)$ は $\bm x(t)$ に2つの線形演算子 $d^2/dt^2$ と $-A$ を適用した結果が等しくなることを要求している。
そこで $\bm x(t)$ が $d^2/dt^2$ と $-A$ との両方に対して固有値 $-\lambda$ を持つ固有ベクトルとなるような特殊な解について考えよう。すなわち、
$$ \begin{cases} \ddot{\bm x}=-\lambda \bm x\\ {}-A\bm x=-\lambda \bm x \end{cases}\tag{**} $$
である。このような $\bm x(t)$ は当然式 $(*)$ を満たす($\ddot{\bm x}=-A\bm x=-\lambda \bm x$)が、この形以外にも解は存在するため「特殊解」と呼んでいる。
まず $-A\bm x=-\lambda \bm x$ の条件について考えよう。この $A$ は実対称行列でありエルミートであるから、$n$ 個の実数固有値 $\lambda_1,\lambda_2,\dots,\lambda_n$ と、 それらに対応した互いに直交する固有ベクトル $\bm e_1,\bm e_2,\dots,\bm e_n$ とを求められるはずである。
$$ {}-A\bm e_N=-\lambda_N\bm e_N\hspace{5mm}(N=1,2,\dots,n) $$
この $\bm e_N$ に対して $\bm x_N(t)\parallel\bm e_N$ すなわち
$$\bm x_N(t)=\tau_N(t)\bm e_N$$
と置けば $\tau_N(t)$ の中身にかかわらず
$$ {}-A\bm x_N=-\lambda_N\bm x_N $$
が成り立つ。一方で、
$$ \ddot{\bm x}_N=-\lambda_N \bm x_N $$
は、
$$ \ddot\tau_N(t)\bm e_N=-\lambda_N\tau_N(t)\bm e_N $$
すなわち
$$ \ddot\tau_N(t)=-\lambda_N\tau_N(t) $$
であれば満たされる。以下に見るように上記の $A$ に対しては $\lambda_N>0$ となる。そこで、
$$ \bm x_N=\underbrace{a_N\cos(\sqrt{\lambda_N}\,t+\theta_N)}_{\tau_N(t)}\bm e_N $$
と取ればこれが方程式 $(**)$ の解となる。
$n$ 個の固有値に対応する $\bm x_N(t)$ が求まれば $(*)$ の一般解はこれら特殊解の重ね合わせ(線形結合)として
$$ \bm x(t)=\sum_{N=1}^n \bm x_N(t) $$
のように表すことができる。
変数分離と同じである †
上記の手順は変数分離による多変数微分方程式の解法と同じである。
$\bm x$ の $j$ 成分 $x_j(t)$ を $j$ と $t$ との2変数関数と考えて $x(j,t)$ と書こう。
この $x(j,t)$ が $t$ 依存性を表す $\tau(t)$ と $j$ 依存性を表す $e_j$ とに分離可能であると仮定して、
$$ x(j,t)=\tau(t)e(j) $$
と置き運動方程式に代入すれば、
$$ \frac{d^2}{dt^2}\tau(t)e(j)=-\tau(t)\frac KM\big[-e(j-1)+2e(j)-e(j+1)\big] $$
両辺を $x(j,t)=\tau(t)e(j)$ で割ると、左辺は $t$ のみの関数、右辺は $j$ のみの関数となるから実際には定数でなければならず、それを $-\lambda$ と置く。
$$ \frac{\frac{d^2}{dt^2}\tau(t)}{\tau(t)}=-\frac KM\frac{-e(j-1)+2e(j)-e(j+1)}{e(j)}=-\lambda $$
これは $\tau(t), e(j)$ がそれぞれ対応する線形演算子の固有値 $-\lambda$ に対する固有関数であることを意味する。
$$ \frac{d^2}{dt^2}\tau(t)=-\lambda\tau(t) $$
$$ {}-\frac KM\big[-e(j-1)+2e(j)-e(j+1)\big]=-\lambda e(j)\ \ \leftrightarrow\ \ -A\bm e=-\lambda\bm e $$
変数分離による微分方程式の解法は線形演算子の同時固有関数を求めることに対応していたのである。
$A$ に対する固有値問題を解く †
一般の $n$ に対して $|A-\lambda I|=0$ を直接解くのは難しいため、ここでは $A$ が $j$ に対する二階差分に相当することを利用して固有値問題を解くことにする。
$j$ による二階差分を $\frac{\Delta^2}{\Delta j^2}$ と書くことにすれば、求めたい固有ベクトル $\bm e=\big(e_j\big)$ は
$$ {}-\frac KM(-e_{j-1}+2e_j-e_{j+1})=\frac KM\frac{\Delta^2}{\Delta j^2} e_j=-\lambda e_j $$
を満たす必要がある。
後に分かるように $\lambda>0$ であることを先取りすると、
$$ \frac{d^2}{dt^2}\tau(t)=-\lambda\tau(t) $$
の一般解が
$$ \tau(t)=a \cos(\sqrt\lambda \,t+\theta) $$
であることに対応して、上の差分方程式には
$$ e_j=\sin (k\,j) $$
の形の解が存在する。
ここで $\cos(kj+\theta)$ ではなく $\sin(kj)$ とした理由は固定端条件 $j=0$ において $e_0=0$ を満たすためである。
実際にこれが方程式を満たすことを確認しよう。
$$ e_{j\pm 1}=\sin \big(k(j\pm 1)\big)=\pm\sin(k)\cos(kj)+\cos(k)\underbrace{\sin(kj)}_{e_j} $$
であるから、
$$ \frac{\Delta^2}{\Delta j^2}e_j=e_{j+1}-2e_j+e_{j-1}=\underbrace{-2(1-\cos k)}_{\text{固有値}} e_j $$
を得る。上式と比較すればこのようにして作った $\bm e$ は固有値
$$ \lambda=\frac {2K}M(1-\cos k) $$
に対する $A$ の固有ベクトルの候補となることが分かる。
候補と書いたのは、$k$ や $\lambda$ は任意の値を取れるわけではないからである。もう一方の固定端条件 「$j=n+1$ において $e_{n+1}=0$」を満たさなければならないことから、以下のように離散的な $n$ 個の値のみが許されることになる。
$$ e_{n+1}=\sin\big(k(n+1)\big)=0 $$
は、ある整数 $N$ に対して
$$ k(n+1)=N\pi $$
を満たすことを意味する。
そこで、$N$ を指標として対応する $k,\lambda$ を
$$ k_N=\frac{N\pi}{n+1} $$
$$ \lambda_N=-\frac {2K}M\Big[1-\cos \Big(\frac{N\pi}{n+1}\Big)\Big] $$
と書くことにしよう。
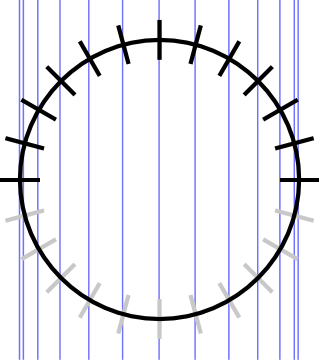
$n=11$ の状況を示した右図からも分かる通り、一般に $\cos(\theta+2\pi)=\cos\theta$ と $\cos(-\theta)=\cos \theta$ が成り立つことを反映して、$\displaystyle\cos \Big(\frac{N\pi}{n+1}\Big)$ の値は $N$ の変化に対して繰り返し同じ値を取ることになる。すべての可能な値を得るには
$$ 0\le \frac{N\pi}{n+1}\le \pi $$
すなわち、
$$ 0\le N\le n+1 $$
の範囲のみを考えれば十分であり、範囲外の $N$ はこれらと重複する $\lambda_N$ しか与えない。
さらに、$N=0,n+1$ はそれぞれ $k_N=0,\pi$ に対応するが、このときすべての $j$ に対して $e_j=\sin(k_N j)=0$ すなわち $\bm e_N=\bm 0$ となって有効な固有ベクトルを与えない。
したがって、独立な $\lambda_N$ の値は $N=1,2,\dots,n$ に対応する $n$ 種類に限られる。
以上より、$N=1,2,\dots,n$ に対して
$$ \bm x_N(t)=\cos(\sqrt{\lambda_N}\,t+\theta)\begin{pmatrix} \sin 1k_N\\ \sin 2k_N\\ \vdots\\ \sin nk_N\\ \end{pmatrix} $$
ただし、
$$ k_N=\frac{N\pi}{n+1} $$
$$ \lambda_N=\frac {2K}M\big(1-\cos k_N\big) $$
と置けば、
$$ \ddot {\bm x}_N(t)=-A\bm x_N(t)=-\lambda_N\bm x_N(t) $$
を満たす $n$ 個の異なる実数固有値とそれに対応する $n$ 個の解が得られることが分かった。$A$ は $n$ 次エルミート行列であるから固有値はこれ以外に存在せず、互いに異なる固有値に属するこれらの $n$ 個の固有ベクトルは互いに直交することになる。先に仮定した通り $\lambda_N>0$ が成り立っていることにも注意せよ。
元々の方程式 $(*)$ の一般解はここで求めた $n$ 個の特殊解 $\bm x_N(t)$ の線形結合として
$$ \sum_{N=1}^n a_N\bm x_N(t) $$
のように表せる。つまりこの系の任意の運動は $\bm x_N(t)$ の重ね合わせとして記述可能である。
固有ベクトルからなる特殊解の物理的意味 †
上で求めた $\bm x_N(t)$ は時間依存性 $\tau(t)$ と空間依存性($j$ 依存性) $\bm e=\big(e_j\big)$ が分離されており、
- すべての粒子が時刻に対して同じ振動数、同じ位相で正弦波的に振動する
- 振動の振幅と符号のみ空間的に分布を持つ
という著しい特徴を持っている。
このような振る舞いは「固有振動モード」あるいは単に「振動モード」と呼ばれ、この系の任意の運動は固有振動モードの重ね合わせで表されることになる。
この系における振動モードの空間的な形状は、
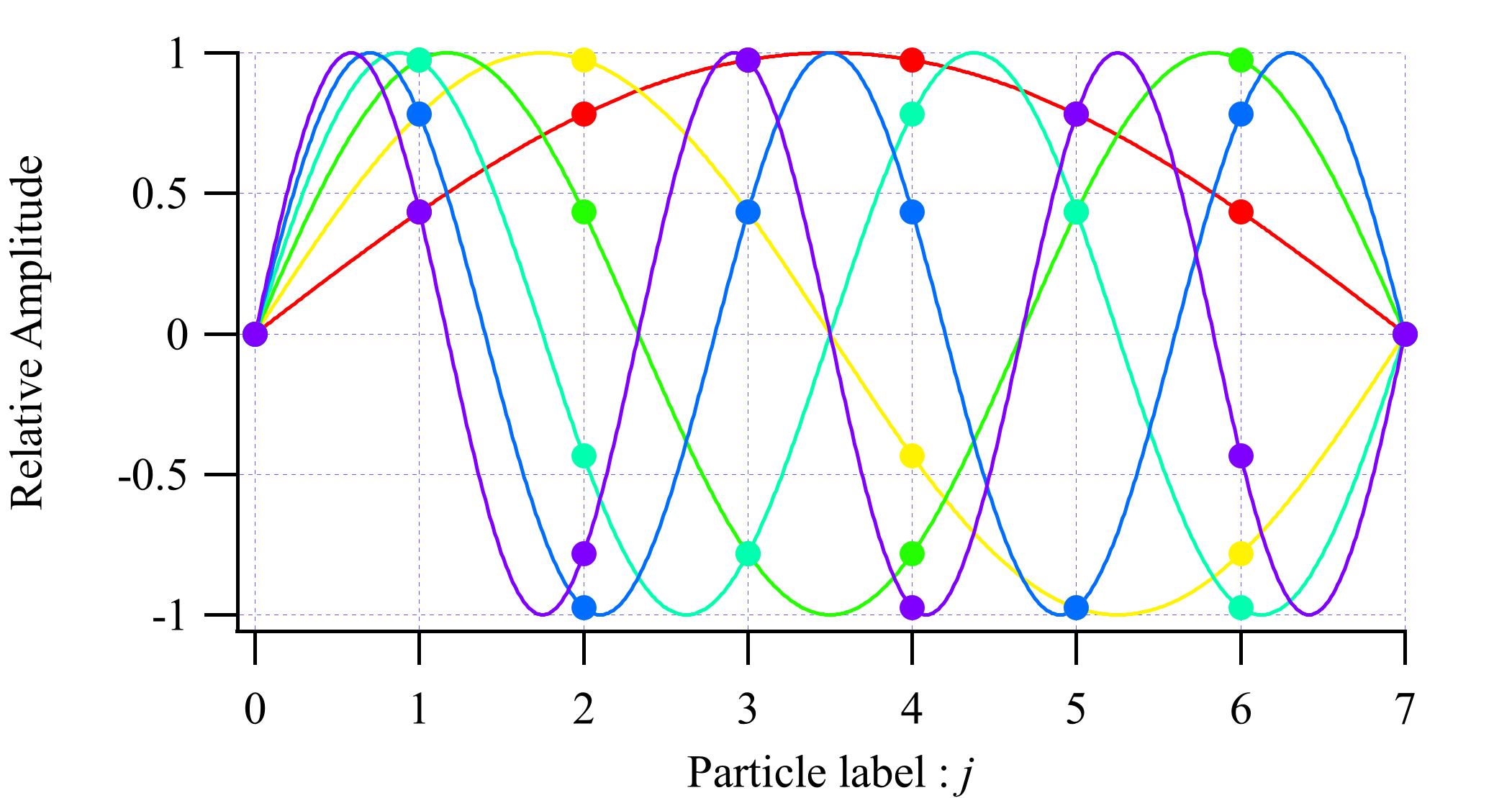
$$ \bm e_N=\begin{pmatrix} \sin 1k_N\\ \sin 2k_N\\ \vdots\\ \sin nk_N\\ \end{pmatrix} $$
で与えられ、これは $x_0=x_{n+1}=0$ に固定端を有する正弦波となっている。
$n=6$ に対して $e_j$ をグラフに示した。$N=1,2,\dots,6$ に対応する6本の正弦波が描かれており、$j=0,1,\dots,n+1$ と交わったところに描かれた●マークの縦軸の値が $j$ 番目の重りの振幅(符号を含む)に相当する。すべてのモードが $j=0$ と $j=n+1$ に節を持っており、$N$ 番目のモードは $N$ 個の腹を持つことを確認できる。
実際の振動の様子は下図のようになる。 それぞれの $N$ に対して、すべての粒子が同じ角振動数および位相を持って振動していることを確認できるだろうか。また、異なる $N$ を比べれば波長の短いモード、つまり波数の大きなモードほど速く振動することも確認してほしい。
LANG: p5js_live
const sk = sketch;
let n = 6;
let t = 0;
let w = 600;
let h = 200;
let amp = 0.25;
sk.setup = () => {
sk.createCanvas(w, h);
sk.frameRate(30);
};
const drawSpring = (x1, x2, y, dx, dy) => {
sk.strokeWeight(1);
sk.stroke(0);
const delta = (x2-x1-dx*2/10) / 20;
let x = x1 + dx / 10;
sk.line(x1,y,x,y);
sk.line(x,y,x+delta,y+dy/4);
x+=delta;
for(let i=0; i<4; i++) {
sk.line(x,y+dy/4,x+2*delta,y-dy/4);
x+=2*delta;
sk.line(x,y-dy/4,x+2*delta,y+dy/4);
x+=2*delta;
}
sk.line(x,y+dy/4,x+2*delta,y-dy/4);
x+=2*delta;
sk.line(x,y-dy/4,x+delta,y);
x+=delta;
sk.line(x,y,x2,y);
};
sk.draw = () => {
sk.textSize(15);
sk.background(255);
sk.noStroke();
let dx = (w-20) / (n + 2);
let dy = (h-20) / n;
for(let i=0; i<n; i++){
sk.fill(sk.color('hsl('+sk.round(i/(n+1)*360)+', 100%, 50%)'));
let y = 10 + i * dy;
let k = (i+1)*sk.PI/(n+1);
let w = sk.sqrt((1-sk.cos(k)));
sk.text('N = '+(i+1), 0, y+5);
for(let j=0; j<=n+1; j++){
let delta = sk.sin(k*j) * sk.cos(w*t);
let x = 60 + (j + amp * delta) * dx;
if(j < n+1) {
let xNext = 60 + (j + 1 + amp * sk.sin(k*(j+1)) * sk.cos(w*t)) * dx;
drawSpring(x, xNext, y, dx, dy);
}
sk.strokeWeight(0);
sk.ellipse(x,y,10,10);
}
}
sk.fill(0);
sk.text('j = ', 18, (h-10));
for(let j=0; j<=n+1; j++){
let x = 55 + j * dx;
sk.text(j, x, (h-10));
}
t += 0.2;
}
分散関係 †
波数と振動数との関係はしばしば分散関係と呼ばれる。
この系では $N$ 番目のモードの角振動数を $\omega_N$ とすれば、
$$ \omega_N^2=\lambda_N=\frac{2K}M\big(1-\cos k_N\big)=\frac{4K}M\sin^2 \frac{k_N}2 $$
すなわち、
$$ \omega_N=2\sqrt\frac{K}M\sin \frac{k_N}2 $$
が分散関係を与える。
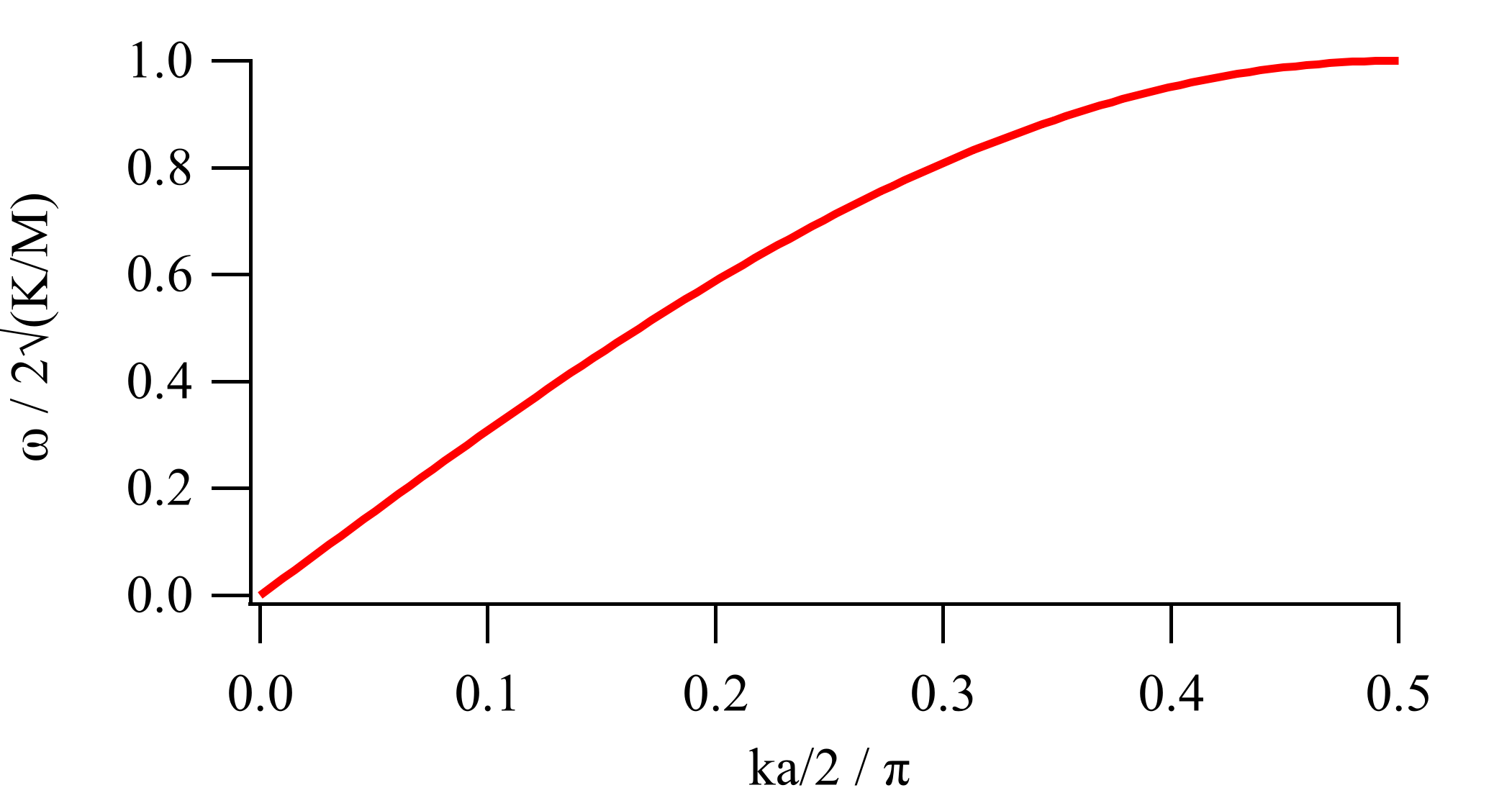
ただし上の定義の $k_N$ は波数そのものではないことに注意が必要。バネ1つ分の自然長(格子定数に相当)を $a$ とすれば $k'_N=k_N/a$ が本来の波数に相当し、
$$ \omega_N=2\sqrt\frac{K}M\sin \frac{k'_Na}2 $$
が本来の分散関係となる。
$0<k'_Na/2<\pi/2$ の範囲においては右のグラフのように $k$ の小さいところではほぼ $\omega$ は $k$ に比例するが $k'_Na/2\sim\pi/2$ において飽和が見られる形になる。
たしかに上の動画でも $N=1$ に対して $N=2$ はほぼ2倍の周波数で振動するのに対して、$N=5$ と $N=6$ とはあまり周波数に違いがないことを実感できる。
蛇足:固有関数の直交性 †
$\bm e_N$ はエルミート行列の異なる固有値に対する固有ベクトルであるから、独立であるだけでなく直交する。実際に計算してみると、
$$ \begin{aligned} (\bm e_N,\bm e_{N'}) &\propto\sum_{j=1}^n\sin (k_Nj)\sin (k_{N'}j)\\ &=-\frac12\sum_{j=1}^n\big[\cos\big((k_N+k_{N'})j\big)-\cos \big((k_N-k_{N'})j\big)\big]\\ &=-\frac12\sum_{j=1}^n\Big[\cos \frac{jM\pi}{n+1}-\cos \frac{jM'\pi}{n+1}\Big]\\ \end{aligned} $$
ただし、$M=N+N',M'=N-N'$ となる。すると、$M\ne 0$ に対して
$$ \sum_{j=1}^n\cos \frac{jM\pi}{n+1}= \begin{cases} 0&M\text{が奇数}\\ {}-1&M\text{が偶数} \end{cases} $$
となることと、$M,M'$ の偶奇が等しいことから、
$$ (\bm x_N,\bm x_{N'})=0 $$
が導かれる。
上記の $\cos$ の和は、
$$ \begin{aligned} \sum_{j=1}^n\exp \frac{\pm ijM\pi}{n+1} &=\exp \Big(\frac{\pm iM\pi}{n+1}\Big) \frac{\exp \Big(\frac{\pm inM\pi}{n+1}\Big)-1} {\exp \Big(\frac{\pm iM\pi}{n+1}\Big)-1}\\ &=\exp \Big(\frac{\pm iM\pi}{n+1}\Big) \frac{\exp \Big(\pm iM\pi\pm \frac{-iM\pi}{n+1}\Big)-1} {\exp \Big(\frac{\pm iM\pi}{n+1}\Big)-1}\\ &=\exp \Big(\frac{\pm iM\pi}{n+1}\Big) \frac{(-1)^M\exp \Big(\pm \frac{-iM\pi}{n+1}\Big)-1} {\exp \Big(\frac{\pm iM\pi}{n+1}\Big)-1}\\ &= \frac{(-1)^M-\exp \Big(\frac{\pm iM\pi}{n+1}\Big)} {\exp \Big(\frac{\pm iM\pi}{n+1}\Big)-1}\\ &=\begin{cases} \mp\cot\frac{M\pi}{n+1} &M\text{ が奇数}\\ {}-1&M\text{ が偶数}\\ \end{cases} \end{aligned} $$
から得られる。
おまけ:グリーン関数法 †
この話は「対角化」や「行列の関数」とは関係ないのであるが、線形微分方程式繋がりということでここで紹介しておく。 カリキュラム上、まだ、「デルタ関数」を学んでいない場合には、 デルタ関数やグリーン関数について学んだ後で戻ってきてざっと目を通せば、 グリーン関数法と線形代数との繋がりを理解できるはずである。
線形微分方程式:
$$ Tf(x)=g(x) $$
が、「$x$ に対する微分を含むような線形変換 $T$ を未知の関数 $f(x)$ に 適用すると既知の関数 $g(x)$ になる」を表すとき、これを解いて $f(x)$ を求めることを考える。
$T$ の線形性から、恒等的にゼロとなるような $g(x)=0$ を与えれば $f(x)=0$ が解となってしまうため($T$ が正則でなければこれ以外に解はあるかもしれないが)、このような $g(x)$ は $f(x)$ の
このような問題は $T$ が正則であり、
$$TT^{-1}=I$$
を満たすような $T^{-1}$ を求めることさえできれば両辺に $T^{-1}$ をかけることで
$$ f(x)=T^{-1}g(x) $$
として簡単に解ける。
「グリーン関数法」では「グリーン関数」と呼ばれる関数を使って $T^{-1}$ を求め、方程式を解く。
$T$ のグリーン関数とは、$T$ を適用すると ディラックのデルタ関数 を生じるような関数すなわち、
$$ TG(x,x')=\delta(x-x') $$
を満たすような関数 $G(x,x')$ のことである。 (細かいことを言うと この微分方程式に加えて、 元の問題で与えられる境界条件も満たすものでないとならない)
この $G(x,x')$ を使うと、
$$T^{-1}:\rho(x)\mapsto\int G(x,x')\rho(x')dx'$$
と書けるため、
$$ f(x)=\int G(x,x')g(x')dx' $$
が微分方程式の解になる、というのがグリーン関数法のキモである。
実際にこれが $TT^{-1}=I$ を満たすことを、任意の関数 $f(x)$ に対して、
$$ \begin{aligned} TT^{-1}f(x)&=T\int G(x,x')f(x')dx'\\ &=\int TG(x,x')f(x')dx'\\ &=\int \delta(x-x')f(x')dx'\\ &=f(x)\\ \end{aligned} $$
となることから確かめられる。
ここで、
$$ I:f(x)\mapsto\int\delta(x-x')f(x')dx' $$
と書かれたことと、単位行列の要素がクロネッカーのデルタ $\delta_{ij}$ を用いて $I=\big(\delta_{ij}\big)$ と書け、$\bm y=I\bm x$ の要素が
$$ y_{i}=\sum_{j=1}^n\delta_{ij}x_j $$
と書かれたこととが対応している点も良く理解しておくように。
例 †
電荷密度分布 $\rho(\bm x)$ の作る電位 $\phi(\bm x)$ を求めたい。
基本方程式はポアソン方程式
$$-\nabla^2\phi(\bm x)=\frac1\epsilon_0\rho(\bm x) $$
で与えられるが、この方程式は
$$ \underbrace{-\epsilon_0\nabla^2}_T\phi(\bm x)=\rho(\bm x) $$
としたときの線形演算子 $T$ の逆 $T^{-1}$ を求めれば $\phi(x)=T^{-1}\rho(x)$ として解ける。
$\bm x'$ に置かれた単位点電荷の作る電位を無限遠で $\phi(\bm x)=0$ となる境界条件の下で解けば、
$$ \phi_1(\bm x;\bm x')=-\frac{1}{4\pi\epsilon_0}\frac{1}{|\bm x-\bm x'|} $$
となるが、これは
$$ T\phi_1(\bm x;\bm x')=\delta^2(\bm x-\bm x') $$
を表しており、$T$ に対する同境界条件を満たすグリーン関数が $G(\bm x,\bm x')=\phi_1(\bm x;\bm x')$ であることを表している。
したがって、任意の電荷分布 $\rho(\bm x)$ の作る電位を
$$ \begin{aligned} \phi(\bm x)&=T^{-1}\rho(\bm x)=\iiint G(\bm x,\bm x')\rho(\bm x')d^3\bm x'\\ &=-\frac{1}{4\pi\epsilon_0}\iiint \frac{\rho(\bm x')}{|\bm x-\bm x'|}d^3\bm x'\\ \end{aligned} $$
のようにして求められるのである。
この式の物理的な意味は、各点における電荷密度が作る電位を重ね合わせることで全体としての電位が求まる、と読めるが、重ね合わせることが可能な理由は $T$ の線形性にあることを理解せよ。
非線形な方程式ではこのような「重ね合わせ」は通用しない。
質問・コメント †
無題 †
()
むずかっしー
*1 参考:http://w3e.kanazawa-it.ac.jp/math/physics/category/mechanics/masspoint_mechanics/simple_harmonic_motion/henkan-tex.cgi?target=/math/physics/category/mechanics/masspoint_mechanics/simple_harmonic_motion/shm_solution.html#solution2
添付ファイル: