量子力学/密度行列
密度行列について †
wikipedia:密度行列、wikipedia:量子もつれ、wikipedia:テンソル積#線型写像のテンソル積 を参考にまとめてみる。
量子状態と混合状態 †
ある定まった量子状態 $|\psi\rangle$ にある1粒子に対してある物理量 $\hat O$ を測定した際の期待値は、
$$\langle O\rangle_\psi=\langle\psi|\hat O|\psi\rangle$$
として求められるのであった。
これは、完全に同一の量子状態 $|\psi\rangle$ を繰り返し生成し、測定を繰り返し、得られた物理量を平均した時に得られる測定値に対応する。
現実には「1つの定まった状態」を繰り返し生成することが難しい場合も多く、その場合には測定ごとに異なる量子状態が生成されてしまうことになる。それでも、「ある量子状態 $|\psi_j\rangle$ にいる粒子が生成される確率が定数 $p_j$ で表せる初期化方法」が実現可能であるとすれば、そのように初期化された状態に対する測定の期待値を考えることが意味を持つ。このように、1回1回の測定に対しては異なる量子状態にいる粒子が生成されるが、その確率的な割合は定まっているような状態のことを「混合状態」と呼ぶ。あるいは同時に存在する多数の粒子が確率 $p_j$ で1粒子状態 $|\psi_j\rangle$ にいるような多粒子状態に対して「一粒子物理量の平均値(あるいは総和)」を測定する状況を考えてもよい。
混合状態 $\rho$ に対する物理量 $\hat O$ の期待値は、個々の量子状態に対する期待値を、さらに $p_j$ で重みづけして足し合わせることで求められる。
$$\langle O\rangle_\rho=\sum_j p_j\langle\psi_j|\hat O|\psi_j\rangle$$
この式に現れる $|\psi_j\rangle$ は必ずしも直交している必要はなく、その混合状態で現れうるすべての状態を列挙していると考えて良い。
ここで、$p_j$ は確率であるから以下の性質を持つ。
$$ \begin{cases} p_j\ge 0\\ \sum_jp_j=1 \end{cases} $$
上の式は量子状態 $|\psi\rangle$ をある正規直交完全系 $|\phi_k\rangle$ で展開して、
$$|\psi\rangle=\underbrace{\bigg[\sum_k |\phi_k\rangle\langle\phi_k|\bigg]}_{\hat 1}|\psi\rangle=\sum_k |\phi_k\rangle\underbrace{\langle\phi_k|\psi\rangle}_{c_k}=\sum_k c_k|\phi_k\rangle$$
と書いた際に、$|\psi\rangle$ に対する期待値を、
$$\langle O\rangle_\psi=\langle\psi|\hat O|\psi\rangle=\sum_k\sum_{k'}c_kc_{k'}\langle\phi_k|\hat O|\phi_{k'}\rangle$$
と書けるのとは全く異なる状況であり、式であることに注意せよ。
密度演算子と密度行列 †
混合状態の期待値の式を適当な正規直交完全系 $|\phi_k\rangle$ を用いて変形すると、
$$ \begin{aligned} \langle O\rangle_\rho &=\sum_jp_j\langle\psi_j|\underbrace{\bigg[\sum_k |\phi_k\rangle\langle\phi_k|\bigg]}_{\hat 1}\hat O|\psi_j\rangle\\ &=\sum_j\sum_k p_j\langle\psi_j|\phi_k\rangle\langle\phi_k|\hat O|\psi_j\rangle\\ &=\sum_k \langle\phi_k|\hat O\underbrace{\bigg[\sum_jp_j|\psi_j\rangle\langle\psi_j|\bigg]}_{\hat\rho}|\phi_k\rangle\\ &=\sum_k \langle\phi_k|\hat O\hat\rho|\phi_k\rangle\\ &=\text{Tr}\big[\hat O\hat\rho\big]=\text{Tr}\big[\hat\rho\hat O\big]\\ \end{aligned} $$
のように、混合状態に関する完全な情報を含む「密度演算子」と呼ばれる量 $\hat\rho$ と $\hat O$ との積に対してトレースを取った形に書き表せることが分かる。
トレースは座標変換に対して保存するため、当然この期待値は $|\phi_k\rangle$ の取り方には依らない。
$\hat\rho$ の定義に出てくる
$$ \hat P_j=|\psi_j\rangle\langle\psi_j| $$
は量子状態 $|\psi_j\rangle$ への射影演算子であるから、$\hat\rho$ は
$$ \hat \rho=\sum_jp_j\hat P_j $$
と書くことができる。
密度演算子を適当な基底に対して行列として表現したものを密度行列と呼ぶ。
密度演算子の性質 †
エルミート性 †
射影演算子はエルミートであるから、その重み付きの和である $\hat\rho$ もエルミートになる。
つまり $\hat\rho^\dagger=\hat\rho$ が成り立つ。
これは密度演算子の固有値が実数であり、異なる固有値に対する固有ベクトルが直交すること、そしてユニタリーな座標変換で対角化可能であること、すなわち固有ベクトルによる正規直交完全系が作れることを保証する。
非負性 †
さらに、任意の状態ベクトル $|\psi\rangle$ に対して、
$$ \langle\psi|\hat \rho|\psi\rangle=\sum_jp_j\langle\psi|\psi_j\rangle\langle\psi_j|\psi\rangle=\sum_jp_j|\langle\psi_j|\psi\rangle|^2\ge0 $$
となる非負性が成り立つ。
これは密度演算子のすべての固有値がゼロ以上であることに対応する。
規格化されたトレース †
また任意の正規直交完全系 $|\phi_k\rangle$ に対して、
$$ \text{Tr}\big[\hat P_j\big]=\sum_k\langle\phi_k|\psi_j\rangle\langle\psi_j|\phi_k\rangle=\sum_k|\langle\phi_k|\psi_j\rangle|^2=\|\psi_j\|^2=1 $$
が成り立つから(後ろから2つ目の等号はパーセバルの等式)、任意の混合状態に対する密度演算子 $\hat \rho$ は
$$ \text{Tr}\big[\hat\rho\big]=\sum_jp_j\text{Tr}\big[\hat P_j\big]=\sum_jp_j=1 $$
を満たす。
これは密度演算子の固有値の総和が1であることに対応する。
密度演算子の対角化 †
$\hat\rho$ の固有ベクトルにより作った正規直交完全系を $|\phi_k\rangle$ とする。
$$ \hat\rho|\phi_k\rangle=\lambda_k|\phi_k\rangle $$
このとき、
$$ \langle\phi_j|\hat\rho|\phi_k\rangle=\lambda_k\langle\phi_j|\phi_k\rangle=\lambda_k\delta_{jk} $$
であり、つまりこの正規直交完全系に対して $\hat\rho$ は対角化された形になる。
ここで、
$$ \hat\rho'=\sum_k \lambda_k|\phi_k\rangle\langle\phi_k| $$
を作れば、
$$ \langle\phi_j|\hat\rho'|\phi_k\rangle=\sum_{k'} \lambda_{k'}\langle\phi_j|\phi_{k'}\rangle\langle\phi_{k'}|\phi_k\rangle=\sum_{k'} \lambda_{k'}\delta_{jk'}\delta_{k'k}=\lambda_k\delta_{jk} $$
であるから、
$$\hat\rho'=\hat\rho$$
が成り立つことになる。($\hat\rho'$ の表式は $\hat\rho$ のスペクトル分解である)
この形から、
- 任意の状態 $|\psi_j\rangle$ が確率 $p_j$ で現れるという元の混合状態と、
- 正規直交する状態 $|\phi_k\rangle$ が確率 $\lambda_k$ で現れる混合状態と、
は、任意の物理量に対する測定で同一の期待値を与える。
すなわちどんな測定でも区別をつけることのできない「同一の物理状態」であると言える。
密度演算子の決定性 †
上の議論から、「任意の物理量に対する測定で同一の期待値を与えるような同一の物理状態」に対して、密度演算子がただ1つに定まることもわかる・・・と思ったけど、そんなに単純じゃないか。この部分、あとでもう少し考える。
位相の不確定性が消えている †
同一の物理状態に対して、密度演算子についてはただ1つの形が定まる、ということの意味は、波動関数ではある量子状態 $|\psi\rangle$ と、位相のみが異なる $|\psi'\rangle=e^{i\theta}|\psi\rangle$ と、が同一の物理的状態を表すにもかかわらず異なる表記になっていたことと対比して理解したい。
これら2つの量子状態に対して射影演算子を作れば
$$ \hat P_{\psi'}=|\psi'\rangle\langle\psi'|=e^{i\theta}|\psi\rangle\langle\psi|\overline{e^{i\theta}} =\cancel{e^{i\theta}}\,|\psi\rangle\langle\psi|\,\cancel{e^{-i\theta}}=|\psi\rangle\langle\psi|=\hat P_\psi $$
となり、確かに位相の不確定性が消えることが分かる。
密度演算子の時間発展 †
$$ \begin{aligned} i\hbar\frac d{dt}\hat\rho &=i\hbar\frac d{dt}\sum_jp_j|\psi_j\rangle\langle\psi_j|\\ &=\sum_jp_j\Big[\Big(i\hbar\frac d{dt}|\psi_j\rangle\Big)\langle\psi_j|+|\psi_j\rangle\Big(i\hbar\frac d{dt}\langle\psi_j|\Big)\Big]\\ &=\sum_jp_j\Big[\Big(\hat{\mathcal H}|\psi_j\rangle\Big)\langle\psi_j|+|\psi_j\rangle\Big(-\langle\psi_j|\hat{\mathcal H}\Big)\Big]\\ &=\hat{\mathcal H}\Big[\sum_jp_j|\psi_j\rangle\langle\psi_j|\Big]-\Big[\sum_jp_j|\psi_j\rangle\langle\psi_j|\Big]\hat{\mathcal H}\\ &=\hat{\mathcal H}\hat\rho-\hat\rho\hat{\mathcal H}\\ &=[\hat{\mathcal H},\hat\rho] \end{aligned} $$
すなわち、
$$ i\hbar\frac d{dt}\hat\rho=[\hat{\mathcal H},\hat\rho] $$
を得る。
純粋状態 †
ある状態を表す密度演算子の固有値が $1$ と $0$ のみであるとき(あるいはスペクトルがデルタ関数的であるとき)、そのような状態を純粋状態と呼ぶ。密度演算子のトレース、すなわち固有値の総和は $1$ なので、純粋状態とは
$$ \hat\rho_j=\hat P_j=|\phi_j\rangle\langle\phi_j| $$
のように密度演算子が1つの射影演算子で書けるような状態のことである。
この純粋状態は「毎回ある定まった量子状態 $|\phi_j\rangle$ が生成されるような混合状態」と同一視できる。
純粋状態の混合 †
2つの純粋状態を表す密度演算子 $\hat\rho_j,\hat\rho_{j'}$ の線形結合
$$ \begin{aligned} \hat\rho&=p_j\hat\rho_j+(1-p_j)\hat\rho_{j'}\\ &=p_j\hat P_j+(1-p_j)\hat P_{j'} \end{aligned} $$
は定義の通り、確率 $p_j$ で $|\psi_j\rangle$ が、確率 $1-p_j$ で $|\psi_{j'}\rangle$ が現れる混合状態を表す。
一般の密度演算子の混合 †
同様に、任意の2つの密度演算子 $\hat\rho,\hat\rho'$ の混合、
$$ \hat\rho''=p\hat\rho+(1-p)\hat\rho' $$
は新しい密度演算子を与えることになる。
なぜなら、それぞれの混合状態をばらしてみれば、それぞれの量子状態が実現する確率を求められるし、確率の総和が1になることも確かめられるためである。
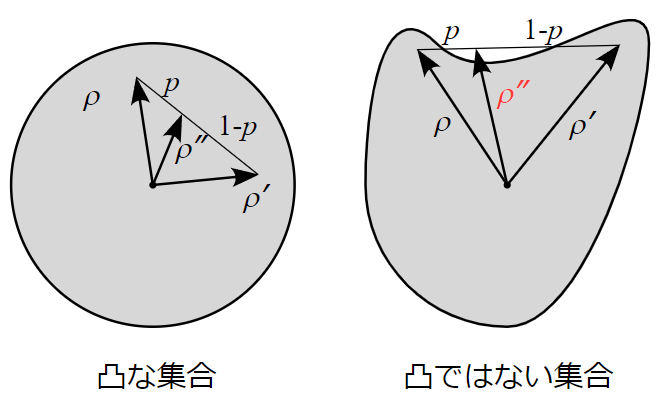
密度演算子集合の凸性 †
上記の性質を指して、「密度演算子の集合は凸である」と言う。
ある集合に含まれる任意の2つのベクトルの「内分点」が必ずその集合に含まれる、というイメージだ。
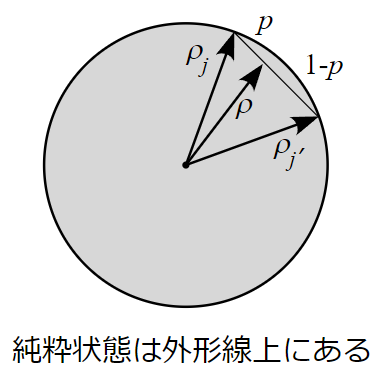
純粋状態は外形線上に †
このイメージからすれば、純粋状態を表す密度演算子はこの凸集合の外形線上にある要素となる。そして任意の2つの密度演算子の内分点は集合の内部の点に対応するため、どんな2つの異なる密度演算子を持ってきても、その線形結合として純粋状態の密度演算子を表すことはできない。(感覚的には明らかだけれど、どうすれば簡単に証明できるか要検討。)
合成系の物理量演算子や密度演算子とテンソル積 †
物理量 $\hat O_A$ が値 $o_A$ を取るときに $1$ となり、そうでなければ $0$ となるような演算子 $\hat O_A(o_A)$ を考える。$\hat O_A(o_A)$ の期待値は、$O_A$ が $o_A$ を取る確率を表すことになる。
実は $\hat O_A(o_A)$ は、$\hat O_A$ の固有値 $o_A$ に対する固有空間 $V(o_A;O_A)$ への射影演算子となる。
これは、$\forall|\psi^\parallel\rangle\in V(o_A;O_A), \forall|\psi^\perp\rangle\in V^\perp(o_A;O_A)$ に対して、
$$ \hat O_A(o_A)|\psi^\parallel\rangle=1|\psi^\parallel\rangle=|\psi^\parallel\rangle $$
$$ \hat O_A(o_A)|\psi^\perp\rangle=0|\psi^\perp\rangle=0 $$
となることから理解できる。
2つの相互に相関の無い物理系 $A,B$ に対応する密度演算子 $\hat\rho_A,\hat\rho_B$ と、それぞれに対する「ある物理量が特定の値をとるときのみ1となる演算子」 $\hat O_A(o_A),\hat O_B(o_B)$ を考える。
系 $A$ と系 $B$ との合成系の密度演算子 $\hat\rho$ と、合成系で $O_A$ が $o_A$ を取り、$O_B$ が $o_B$ を取るときのみ 1 となる演算子 $\hat O_{AB}(o_A, o_B)$ を、
$$\hat\rho=\hat\rho_A\otimes\hat\rho_B$$
$$\hat O_{AB}(o_A,o_B)=\hat O_A(o_A)\otimes\hat O_B(o_B)$$
$$\langle\hat O_{AB}(o_A,o_B)\rangle=\text{Tr}\Big[\hat\rho \hat O_{AB}(o_A,o_B)\Big]= \text{Tr}\Big[\hat\rho_A \hat O_A(o_A)\Big]\times \text{Tr}\Big[\hat\rho_B \hat O_B(o_B)\Big]$$
として求められるような演算 $\otimes$ はテンソル積(外積)と呼ばれる。
簡単に書くと、
$$ \text{Tr}\Big[\big(A\otimes B\big)\big(C\otimes D\big)\Big] =\text{Tr}\Big[AC\Big]\times\text{Tr}\Big[BD\Big] $$
ということ。
さしあたり $2\times 2$ 行列で考える †
天下り的に答えを示せば、
$$ A=\big(a_{ij}\big),B=\big(b_{ij}\big),C=\big(c_{ij}\big),D=\big(d_{ij}\big) $$
と表すとき、
$$ A\otimes B=\Big(a_{ij}B\Big)=\begin{pmatrix} a_{11}B&a_{12}B\\ a_{21}B&a_{22}B\\ \end{pmatrix}=\begin{pmatrix} a_{11}b_{11}&a_{11}b_{12}&a_{12}b_{11}&a_{12}b_{12}\\ a_{11}b_{21}&a_{11}b_{22}&a_{12}b_{21}&a_{12}b_{22}\\ a_{21}b_{11}&a_{21}b_{12}&a_{22}b_{11}&a_{22}b_{12}\\ a_{21}b_{21}&a_{21}b_{22}&a_{22}b_{21}&a_{22}b_{22}\\ \end{pmatrix} $$
のようにテンソル積を定義すると上記の性質が得られる。
確かめてみよう。
$$ \begin{aligned} \text{Tr}\Big[AB\Big]&=\text{Tr}\begin{pmatrix} a_{11}b_{11}+a_{12}b_{21}&a_{11}b_{12}+a_{12}b_{22}\\ a_{21}b_{11}+a_{22}b_{21}&a_{21}b_{12}+a_{22}b_{22}\\ \end{pmatrix}\\ &=a_{11}b_{11}+a_{12}b_{21}+a_{21}b_{12}+a_{22}b_{22}\\ &=\sum_i\sum_j a_{ij}b_{ji} \end{aligned} $$
などに注意しつつ、小行列の記法を使いつつ計算すれば、
$$ \begin{aligned} (A\otimes B)(C\otimes D)&= \begin{pmatrix} a_{11}B&a_{12}B\\ a_{21}B&a_{22}B\\ \end{pmatrix} \begin{pmatrix} c_{11}D&c_{12}D\\ c_{21}D&c_{22}D\\ \end{pmatrix}\\ &=\begin{pmatrix} (a_{11}c_{11}+a_{12}c_{21})BD&(a_{11}c_{12}+a_{12}c_{22})BD\\ (a_{21}c_{11}+a_{22}c_{21})BD&(a_{21}c_{12}+a_{22}c_{22})BD\\ \end{pmatrix} \end{aligned} $$
より、
$$ \begin{aligned} \text{Tr}\Big[\big(A\otimes B\big)\big(C\otimes D\big)\Big] &=(a_{11}c_{11}+a_{12}c_{21})\text{Tr}\big[BD\big]+(a_{21}c_{12}+a_{22}c_{22})\text{Tr}\big[BD\big]\\ &=\text{Tr}\Big[AC\Big]\times\text{Tr}\Big[BD\Big] \end{aligned} $$
任意の次数でも、$A$ の個々の要素と $B$ とを掛けたものを並べた形で外積を定義すればよい。
エンタングル状態 †
上で見た通り、合成系の密度演算子が外積で書けるときには、合成系で $O_A$ が $o_A$ を取り、$O_B$ が $o_B$ を取る確率は、単に系 $A$ で $O_A$ が $o_A$ を取る確率と、系 $B$ で $O_B$ が $o_B$ を取る確率とを掛け算して求められることになる。
これは、「系 $B$ で $O_B$ が $o_B$ を取る確率は系 $A$ における $O_A$ の値によらない」 ということと同じ意味である。このような状況を $\hat\rho_A$ と系 $\hat\rho_B$ との間に相関がないと言う。
エンタングル状態とは、合成系の密度演算子を相関の無い密度演算子上での確率分布として表すことのできない状態のことを言う(らしい)。
$$ \hat\rho_{AB}\ne\sum_i w_i\hat\rho_A^i\otimes \hat\rho_B^i $$
$\hat\rho_A^i$ と $\hat\rho_B^i$ とをどのように取ったとしてもこの形に表せないような密度演算子で書かれる状態がエンタングル状態、というわけだ。
なるほど、わからん。
エンタングル状態の例 †
電子 $A$ のスピンと電子 $B$ のスピンとが必ず反平行となるような状況では、電子 $A$ のスピンの向きを測れば電子 $B$ のスピンの向きは測定せずとも決まってしまう。
そのような状況を、上記のようないくつかの外積密度演算子の上での確率分布として表すことはできないらしい。
まだちょっとピンとこないけど。