量子力学Ⅰ/調和振動子 のバックアップ(No.2)

更新

量子力学Ｉ?

概要 †

spring+mass.png

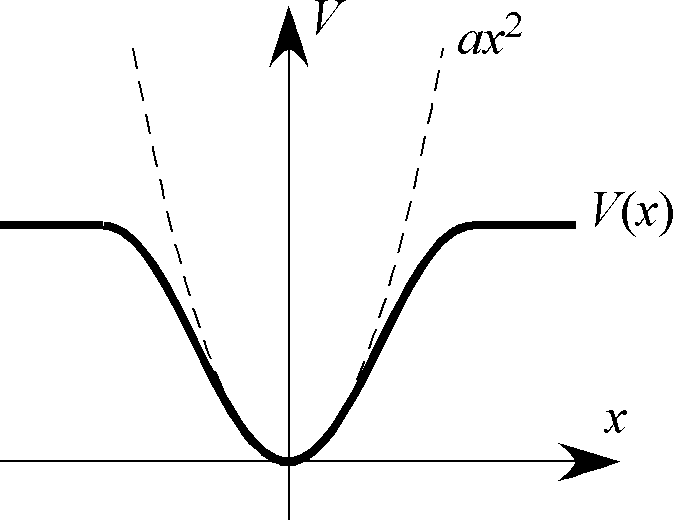
調和振動子とは、理想ばねのように変位に比例する力 f=-kx により束縛された粒子の系である。ポテンシャルエネルギーは V(x)=kx^2/2 となる。 ただしここではばねの自然長位置を x=0 としている。

粒子の質量を m とすれば、古典論では角振動数 \omega=\sqrt{k/m} の単振動

　 x=x_0\cos(\omega t+\delta)

が解であり、エネルギーは E=kx_0^2/2 と表せる。

palabora.png

量子力学的なスケールでそのようなばねを思い浮かべることは難しいが、 一般に任意の滑らかで束縛的なポテンシャルの底を２次関数で近似すれば、 そこでの微小振動は調和振動子と見なせる。

さらに電磁波も、無数の調和振動子の集まりとして表わせることを後に学ぶ。

演習：１次元の調和振動子 †

xi.png

(1) 調和振動子のポテンシャルは V(x)=\frac{1}{2}kx^2 である。 時間に依存しないシュレーディンガー方程式を書け。

(2) このような方程式を解く場合には、変数を無次元化するのが常套手段である。 すなわち、長さの次元を持つ自由変数 x を変数変換して、無次元の量 \xi で記述する。 *1 \xi の書き方は http://kscalar.kj.yamagata-u.a... を参考にした

ここでは、古典論から得られる角振動数を \omega=\sqrt{\frac{k}{m}} として、

　 \xi=\sqrt{\frac{m\omega}{\hbar}}x , \lambda=\frac{2E}{\hbar\omega}

と置くと良い。このとき(1)の式が

　&math( \left(-\frac{d^2}{d\xi^2}+\xi^2-\lambda\right)\psi(\xi)=0 );

となることを示せ。

(3) \xi の大きなところでは \xi^2\gg\lambda となるから、 そこでは \psi は近似的に次の方程式を満たす。

　&math( \frac{d^2}{d\xi^2}\psi(\xi)=\xi^2\psi(\xi) );

ここから予想される

　&math( \psi(\xi)=X(\xi)e^{\pm\xi^2/2} );

を上式に代入し、 X(\xi) に対する条件

　&math( X''(\xi)=2\xi X'(\xi)+(1-\lambda) X(\xi) );

を導出せよ。（系が x=0 付近に束縛されていることから、複号は負を取れ）

(4) X(\xi)=\sum_{l=0}^\infty c_l\xi^l と置いて (3) の式に代入し、 係数 c_l の漸化式

　 c_{l+2}=\frac{2l+1-\lambda}{(l+2)(l+1)}c_l

を導け。

さて、(4) により、 c_0 を決めると c_2,c_4,c_6,\dots が、 c_1 を決めると c_3,c_5,c_7,\dots が、 それぞれすべて決まる。

c_l が途中でゼロにならない場合、漸化式より l\to \infty において

　 \frac{c_{l+2}}{c_l}=\frac{2l+1-\lambda}{(l+2)(l+1)}\to \frac{\,2\,}{l}

が成り立ち、これは

　 2\xi^2 e^{\xi^2}=\sum_{n=1}^{\infty}\frac{2^n}{(2n-2)!!}\xi^{2n} 　あるいは、 　 2\xi e^{\xi^2}=\sum_{n=1}^{\infty}\frac{2^n}{(2n-2)!!}\xi^{2n-1}

の係数の比と同じである。このようになっていては X(\xi)e^{-\xi^2/2} が \xi\to\pm\infty でゼロに収束する(束縛されている)という境界条件を満たさない。

かといって c_0=c_1=0 では \psi(x)=0 になってしまうから、 c_0\ne 0 あるいは c_1\ne 0 である。

境界条件を満たすのは、ある n\ge 0 において c_n\ne 0 であるものの 2n+1-\lambda=0 が成立することにより、 それ以降の l>n ですべて c_l=0 となる場合である。 このとき、 c_0 あるいは c_1 の片方はゼロでなくて構わないが、 もう一方はゼロでなければならない。

(5) n\ge 0 を量子数として \lambda_n,E_n を n,\hbar,\omega で表わせ。

(6) X_4(\xi) を求めよ。規格化はしなくて良い。

エネルギー固有値 †

E_0=\hbar\omega/2 がゼロ点エネルギーとなる。 すなわち、調和振動子は基底状態においても運動エネルギー、ポテンシャルエネルギーがゼロではない。

また、 E_{n+1}-E_n=\hbar\omega より、エネルギー固有値は等間隔に並ぶ。

ここでは示さないが、古典論と同様にポテンシャルエネルギーの期待値は E_n/2 であり、
運動エネルギーの期待値も E_n/2 であり、両者は等しくなる。

固有関数 †

  • n=0 のとき X_0(\xi)=c_0
  • n=1 のとき X_1(\xi)=c_1\xi
  • n=2 のとき X_2(\xi)=c_0\left(1-2\xi^2\right)
  • n=3 のとき X_3(\xi)=c_1\left(\xi-\frac{2}{3}\xi^3\right)
  • n=4 のとき X_4(\xi)=c_0\left(1-4\xi^2+\frac{4}{3}\xi^4\right)
  • ・・・

明らかに X_{2n}(\xi)e^{-\xi^2/2} は偶関数であり、 X_{2n+1}(\xi)e^{-\xi^2/2} は奇関数である。

ここでもポテンシャルの対称性を反映してパリティの異なる固有関数が交互に現れる。

エルミート多項式 †

X_n(\xi) はエルミート多項式と呼ばれる一連の多項式 H_n(\xi) の定数倍になっている。

ただし H_n(\xi) は、母関数 S(\xi,t) をテイラー展開した際に現れる係数として定義される。

　&math( S(\xi,t)=e^{-t^2+2\xi t}=\sum_{n=0}^\infty\frac{1}{n!}H_n(\xi)t^n );

上の X_n(\xi) に対する方程式の \lambda を n で書き換えれば、 H_n(\xi) は次の方程式を満たさなければならない。

　 \Big(\frac{d^2}{d\xi^2}-2\xi\frac{d}{d\xi}+\underbrace{2n}_{\lambda-1}\Big)H_n(\xi)=0

H_n(\xi) がこれを満たすことは、 母関数を \xi や t で微分した形を調べることで証明できる。 → 詳しくはこちら?

また関数系 H_n(\xi)e^{-\xi^2/2} の漸化式、

　&math( H_{n+1}(\xi)e^{-\xi^2/2}=\left(\xi-\frac{d}{d\xi}\right)\left(H_n(\xi)e^{-\xi^2/2}\right) );

　&math( 2nH_{n-1}(\xi)e^{-\xi^2/2}=\left(\xi+\frac{d}{d\xi}\right)\left(H_n(\xi)e^{-\xi^2/2}\right) );

直交性、

　&math(\int_{-\infty}^\infty H_n(\xi)e^{-\xi^2/2}H_m(\xi)e^{-\xi^2/2}d\xi= \left\{\begin{array}{ll} 0&n\ne m\\ 2^nn!\sqrt\pi & n=m \end{array}\right. );

なども母関数を使って証明できる。 → 詳しくはこちら?

H_0(\xi)=1 および漸化式を用いれば、

  • H_0(\xi)=1
  • H_1(\xi)=2\xi
  • H_2(\xi)=-2+4\xi^2
  • H_3(\xi)=-12\xi+8\xi^3
  • H_4(\xi)=12-48xi^2+16\xi^4
  • H_5(\xi)=120\xi-160\xi^3+32\xi^5
  • H_6(\xi)=-120+720\xi^2-480\xi^4+64\xi^6
  • ・・・

が得られる。

固有関数の性質 †

上記エルミート多項式の直交性を表わす式から \psi_n(x) を正規化できて、

　 \psi_n(x)=\sqrt{\frac{\sqrt\pi}{2^nn!}\sqrt{\frac{\hbar}{m\omega}}}H_n\Big(\sqrt{\frac{m\omega}{\hbar}}x\Big)\exp\Big(-\frac{m\omega}{2\hbar}x^2\Big)

このとき正規直交性は、

　 \int_{-\infty}^\infty\psi_n(x)\psi_m(x)dx=\delta_{nm}

漸化式は、

　&math( \sqrt{\frac{m\omega}{2\hbar}}\left(x-\frac{\hbar}{m\omega}\frac{d}{dx}\right)\psi_n(x)=\sqrt{n+1}\,\psi_{n+1}(x) );

　&math( \sqrt{\frac{m\omega}{2\hbar}}\left(x+\frac{\hbar}{m\omega}\frac{d}{dx}\right)\psi_n(x)=\sqrt{n}\,\psi_{n-1}(x) );

となる。

この漸化式は \hat p=\frac{\hbar}{i}\frac{d}{dx} を用いて、

　 \hat a=\sqrt{\frac{m\omega}{2\hbar}}\left(x+\frac{i}{m\omega}\hat p\right)

　 \hat a^\dagger=\sqrt{\frac{m\omega}{2\hbar}}\left(x-\frac{i}{m\omega}\hat p\right)

を定義すれば、*2教科書では２つ目の式が \hat a^* として書かれているが、 \hat p^*\ne \hat p なので正しくない。 \hat p^\dagger= \hat p 、 i^\dagger=-i なので \hat a^\dagger と書くのが正しい。

　 \hat a^\dagger\psi_n(x)=\sqrt{n+1}\,\psi_{n+1}(x)

　 \hat a\psi_n(x)=\sqrt{n}\,\psi_{n+1}(x)

と書ける。ここから、

　 \hat a^\dagger\hat a\psi_n(x)=n\psi_n(x)

　 \hat a\hat a^\dagger\psi_n(x)=(n+1)\psi_n(x)

　 (\hat a\hat a^\dagger-\hat a^\dagger\hat a)\psi_n(x)=\psi_n(x)

　 \hbar\omega(\hat a^\dagger\hat a+1/2)\psi_n(x)=\frac{\hbar\omega}{2}(\hat a\hat a^\dagger+\hat a^\dagger\hat a)\psi_n(x)=\hbar\omega(n+1/2)\psi_n(x)=E_n\psi_n(x)

が得られる。これらを

　 \hat a^\dagger\hat a=\hat n

　 \hat a\hat a^\dagger-\hat a^\dagger\hat a=\hat 1

　 \hbar\omega(\hat a^\dagger\hat a+1/2)\psi_n(x)=\frac{\hbar\omega}{2}(\hat a\hat a^\dagger+\hat a^\dagger\hat a)=\hat H

のように書くこともできる。

３次元の調和振動子 †

*1 \xi の書き方は http://kscalar.kj.yamagata-u.ac.jp/~endo/greek/zeta_xi.html を参考にした
*2 教科書では２つ目の式が \hat a^* として書かれているが、 \hat p^*\ne \hat p なので正しくない。 \hat p^\dagger= \hat p 、 i^\dagger=-i なので \hat a^\dagger と書くのが正しい。
Counter: 165712 (from 2010/06/03), today: 6, yesterday: 0