量子力学Ⅰ/電子の波動方程式 のバックアップ(No.4)
更新- バックアップ一覧
- 差分 を表示
- 現在との差分 を表示
- ソース を表示
- 量子力学Ⅰ/電子の波動方程式 へ行く。
private/量子力学I/前期量子論?
波動方程式 †
電子は粒子と波の両方の性質を持つことが分かってきた。
量子力学では電子の波動方程式を考えることで、電子の運動を記述する。
電子の粒子性 †
電子は水素原子の約1/1000の重さを持つ粒子として振る舞う。
JJ トムソンの実験などでその粒子的な性質は明らかである。
- 運動エネルギーと運動量の関係
電子の波動性 †
電子線回折などによって、電子が回折現象を起こすこと、加速度により波長が異なること、などが示された。
- 運動エネルギーと周期の関係
- 運動量と波数の関係
準備:波動を表わす関数 †
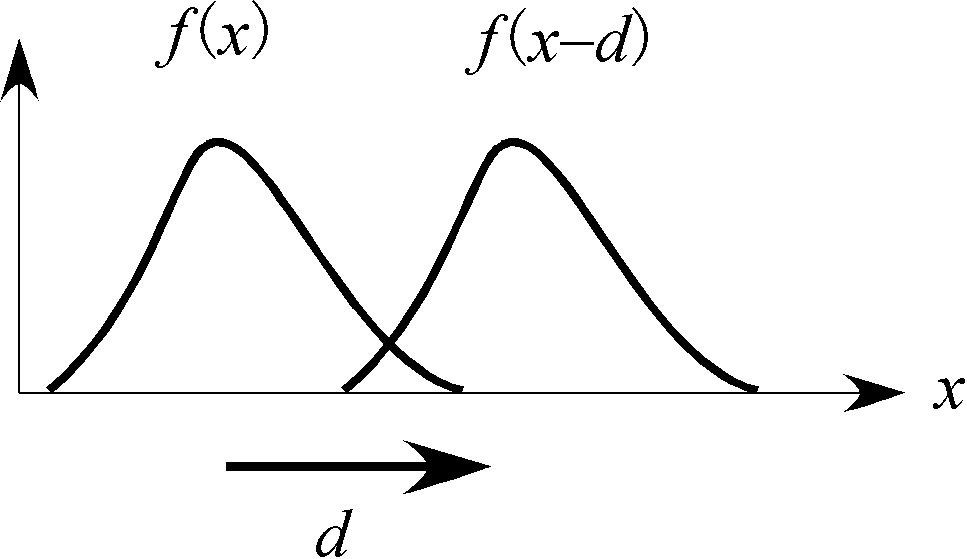
速度 $v$ で移動する関数 †
は、 を の正方向に だけ移動した関数になる。
は が時刻 において だけ移動した関数、 すなわち、 の関数が形を変えずに の正方向に速度 で伝播する関数になる。
位相速度 $v$ で伝播する波(一次元) †
は、波数 の正弦波が速度 で伝播する関数になる。
が波長 、 波数 の正弦波であることに注意せよ。
と書けば、 この関数は時間に対して角振動数 で振動することが分かる。
速度 の波が1周期 の間に進む距離が波長 だから、
両者の逆数を取って、
を確かめられる。
位相速度 $v$ で伝播する平面波(三次元) †
3次元空間で定義された という関数は 軸方向に進む平面波を表わす。
以下では、3次元空間内で任意の方向に進む平面波を考える。
のとき、 は の 方向成分の長さ
という方程式は、 に平行で、原点から 方向に だけ離れた平面を表わす方程式
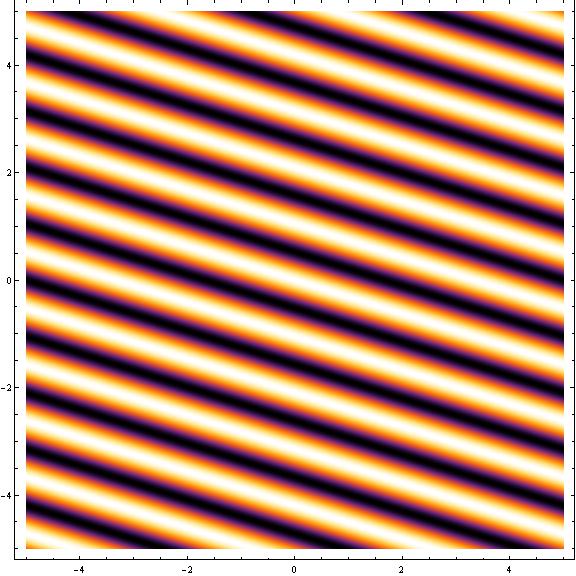
したがって、 は、 方向に波長 の正弦波で、 に垂直方向には一定値を取る平面的な波を表わす。 (下図は二次元の場合)
と書けるから、 これは の 方向成分に、 をかけた値になる。
すなわち、 は、 方向に波長 、波数 の正弦波を表わす。
さらに、 とすれば、 より、 波数 、周期 、速度(位相速度) で伝播する平面波を表わす。
演習:波動方程式(電磁波の場合) †
平面波 が電磁波の波動方程式
を満たすことを示したい。
(1) となることを示せ
(2) となることを示せ
(3) となるためには と の間にどのような関係が必要か
(4) 速度 で進む波の周期 と波長 との間には の関係がある(1回振動する間に進む距離が波長である)。 をそれぞれ で書き直して、(3) と同じ式が得られることを示せ
(5) より一般に、任意の関数 に対して、 が を満たすことを示せ
自由な電子の波動方程式 †
外力を受けない(自由な)電子の満たすべき波動方程式はどのようなものであろうか?
分かっていることは、
- 運動エネルギーと周期の関係
- 運動量と波数の関係
- 運動エネルギーと運動量の関係
を満たす平面波になること。これらを組み合わせると、
という条件が得られる。この条件を満たすような波動方程式を作ろう!
波を と置いてみると、
となって、上の式では 、下の式では が現れてきてしまうため、 と の間の式にしづらい・・・ や は微分により形が変わってしまうのが問題。
微分で形の変わらない関数を使えば波動方程式が作れそう。
→
と置けば、これも波数
、各週波数
の波動を表わす
これらを用いて の関係を表わすと、
これが自由な電子に対するシュレーディンガー方程式である。
外力を受ける場合 †
電子に外力がかかるとき、電子の感じるポテンシャルエネルギーを とすると、 電子のエネルギーは
となる。そこで、シュレーディンガー方程式も、
となる。