線形システム入門 のバックアップ(No.3)

線形性 †

あるシステムに入力と出力があるとします。

　　&uml( skinparam handwritten true skinparam componentStyle rectangle 入力 -> [システム] [システム]-right-> 出力 );

$x$ を入れると $X$ が出て、

　　&uml( skinparam handwritten true skinparam componentStyle rectangle () "<i>x</i>" as IN () "<i>X</i>" as OUT IN -> [システム] [システム]-right-> OUT );

$y$ を入れると $Y$ が出るとき、

　　&uml( skinparam handwritten true skinparam componentStyle rectangle () "<i>y</i>" as IN () "<i>Y</i>" as OUT IN -> [システム] [システム]-right-> OUT );

(1) $x+y$ を入れれば必ず $X+Y$ が出る

　　&uml( skinparam handwritten true skinparam componentStyle rectangle () "<i>x</i>+<i>y</i>" as IN () "<i>X</i>+<i>Y</i>" as OUT IN -> [システム] [システム]-right-> OUT );

(2) $kx$ つまり $x$ の $k$ 倍を入れると必ず $kX$ が出る

　　&uml( skinparam handwritten true skinparam componentStyle rectangle () "<i>kx</i>" as IN () "<i>kX</i>" as OUT IN -> [システム] [システム]-right-> OUT );

の両方を満たすシステムを「線形なシステム」と言い、そのような性質を「線形性」と呼びます。

どうして「線形」と呼ぶの？ †

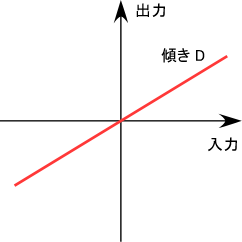
上記のシステムに $1$ を入れた時の出力を $D$ とすると、
線形性により任意の入力 $x=x\cdot 1$ に対する出力は $xD$ になります。

つまり、このシステムは入力に、$1$ に対する出力である $D$ を単に掛け算して出力するだけの単純なシステムであることが分かります。

これ、入力を横軸に、出力を縦軸に取ると比例のグラフ = 原点を通る直線のグラフになるので、「まあ確かに線形だねぇ」と納得できるはずです。

え、それだけ？ †

ということで、入力が１つ、出力が１つしかない線形システムは「単なる定数倍」しかありえなくて、その「定数」は $1$ を入力したときの出力である、ということで、これだけで話は終わりになってしまいます。

でも、入力がたくさん、出力がたくさんあると途端に話が複雑かつ面白くなり、さらにとても幅広く応用の効く内容が現れます。線形システムを扱う数学は線形代数と呼ばれます。

&uml( skinparam handwritten true skinparam componentStyle rectangle () "‥‥" as IN () "‥‥" as OUT 入力1 -> [システム] 入力2 -> [システム] IN -> [システム] 入力n -> [システム] [システム]-right-> 出力1 [システム]-right-> 出力2 [システム]-right-> OUT [システム]-right-> 出力m );

多入出力システムの線形性 †

上記の $n$ 入力 $m$ 出力のシステムが線形である、というのは次の性質を持つことを言います。

$i$ 番目の入力値が $x_i$ であるときに、$i$ 番目の出力が $X_i$ であるとし、

　　&uml( skinparam handwritten true skinparam componentStyle rectangle () "<i>x</i>₁" as IN1 () "<i>x</i>₂" as IN2 () "‥‥" as IN () "<i>x</i>_n" as INn () "<i>X</i>₁" as OUT1 () "<i>X</i>₂" as OUT2 () "‥‥" as OUT () "<i>X</i>_m" as OUTm IN1 -> [システム] IN2 -> [システム] IN -> [システム] INn -> [システム] [システム]-right-> OUTm [システム]-right-> OUT [システム]-right-> OUT2 [システム]-right-> OUT1 );

$i$ 番目の入力値が $y_i$ であるときに、$i$ 番目の出力が $Y_i$ であるとします。

　　&uml( skinparam handwritten true skinparam componentStyle rectangle () "<i>y</i>₁" as IN1 () "<i>y</i>₂" as IN2 () "‥‥" as IN () "<i>y</i>_n" as INn () "<i>Y</i>₁" as OUT1 () "<i>Y</i>₂" as OUT2 () "‥‥" as OUT () "<i>Y</i>_m" as OUTm IN1 -> [システム] IN2 -> [システム] IN -> [システム] INn -> [システム] [システム]-right-> OUTm [システム]-right-> OUT [システム]-right-> OUT2 [システム]-right-> OUT1 );

システムが線形であれば、以下の両方が満たされる。

(1) $i$ 番目の入力が $x_i+y_i$ であれば $i$ 番目の出力は $X_i+Y_i$ である

　　&uml( skinparam handwritten true skinparam componentStyle rectangle () "<i>x</i>₁\n+\n<i>y</i>₁" as IN1 () "<i>x</i>₂\n+\n<i>y</i>₂" as IN2 () "\n‥‥" as IN () "<i>x</i>_n\n+\n<i>y</i>_n" as INn () "<i>X</i>₁\n+\n<i>Y</i>₁" as OUT1 () "<i>X</i>₂\n+\n<i>Y</i>₂" as OUT2 () "\n‥‥" as OUT () "<i>X</i>_m\n+\n<i>Y</i>_m" as OUTm IN1 -> [システム] IN2 -> [システム] IN -> [システム] INn -> [システム] [システム]-right-> OUTm [システム]-right-> OUT [システム]-right-> OUT2 [システム]-right-> OUT1 );

(2) $i$ 番目の入力が $kx_i$ であれば $i$ 番目の出力は $kX_i$ である

　　&uml( skinparam handwritten true skinparam componentStyle rectangle () "<i>ka</i>₁" as IN1 () "<i>ka</i>₂" as IN2 () "‥‥" as IN () "<i>ka</i>_n" as INn () "<i>kA</i>₁" as OUT1 () "<i>kA</i>₂" as OUT2 () "‥‥" as OUT () "<i>kA</i>_m" as OUTm IN1 -> [システム] IN2 -> [システム] IN -> [システム] INn -> [システム] [システム]-right-> OUTm [システム]-right-> OUT [システム]-right-> OUT2 [システム]-right-> OUT1 );

１入力１出力の場合と比べると数が多い分だけ複雑そうに見えますが、

システムを通す前に足したり定数倍するのと、

システムを通した後に足したり定数倍するのと、

結果が同じになる

という性質は変わっておらず、これが線形性のキモになっています。

線形性 = 重ね合わせの原理 †

線形性は、分野によっては重ね合わせの原理、とも呼ばれます。

$a$ に対する出力 $A$ と、
$b$ に対する出力 $B$ と、が分かっていれば、
これらを重ね合わせた $a+b$ に対する出力は、
$a,b$ それぞれが単独であるときの出力 $A,B$ を重ね合わせた $A+B$ になる、ということです。

どんなところに線形システムが現れる？ †

もうほとんどありとあらゆるところに線形システムが現れます。

電気回路をはじめとした信号処理、光や音などの波動、量子力学で中心的な役割を果たしますし、 本来は非線形なシステムに対しても、入力を少しだけ変えた際の応答を線形と見なす「線形近似」を用いた解析が行われることが多く、そこでは線形代数が大活躍します。

入力、出力をベクトルを使って表す †

毎回上記のような絵を描くのは大変なので、 数式を使って書くことを考えます。

$n$ 個の入力 $x_1,x_2,\dots,x_n$ や、$m$ 個の出力 $X_1,X_2,\dots,X_m$ をカッコで括ってひとまとめに書くことにします。

$$ \begin{pmatrix} x_1\\x_2\\\vdots\\x_n \end{pmatrix}, \ \ \begin{pmatrix} X_1\\X_2\\\vdots\\X_m \end{pmatrix} $$

このように数値を縦に並べてカッコで括ったものを数ベクトルと呼びます。

数値を横に並べてカッコで括った、

$$ \begin{pmatrix} x_1&x_2&\dots&x_n \end{pmatrix} $$

のようなものも数ベクトルと呼ばれます。

両者を呼び分ける際には「縦数ベクトル」や「横数ベクトル」と言います。

$n$ 個の数値を並べたベクトルのことを $n$ 次元数ベクトルと呼びます。

ベクトルの足し算、定数倍 †

ベクトル同士の足し算や、ベクトルの定数倍は、上記の線形性を念頭に

$$ \begin{pmatrix}a_1\\a_2\\\vdots\\a_n\end{pmatrix}+ \begin{pmatrix}b_1\\b_2\\\vdots\\b_n\end{pmatrix}= \begin{pmatrix}a_1+b_1\\a_2+b_2\\\vdots\\a_n+b_n\end{pmatrix} $$

および、

$$ k\begin{pmatrix}a_1\\a_2\\\vdots\\a_n\end{pmatrix}= \begin{pmatrix}ka_1\\ka_2\\\vdots\\ka_n\end{pmatrix} $$

と定義します。

この定義から明らかなように、異なる次元のベクトル同士にはベクトルの和は定義されません。

ベクトルを表す文字は太文字で書く †

ベクトルを表す変数はよく太文字で書かれます。

$$ \bm a=\begin{pmatrix} x_1\\x_2\\\vdots\\x_n \end{pmatrix} $$

のような感じ。

「システム」はベクトルの関数 †

上記のような「システム」は、入力 $\bm x$ を与えると出力 $\bm X$ を返すような関数

$$\bm X=f(\bm x)$$

と同一視できます。

1 を入力したときの出力 †

１入力１出力のときには、$1$ を入力したときの出力 $D$ さえ求まれば、 任意の入力に対する出力を求めることができました。

同様に、入力 $n$ 個のシステムの場合にも $\begin{pmatrix}1\\0\\\vdots\\0\end{pmatrix}$ に対する出力が $\bm F_1$ であるなら、

$\begin{pmatrix}x\\0\\\vdots\\0\end{pmatrix}=x\begin{pmatrix}1\\0\\\vdots\\0\end{pmatrix}$ に対する出力は $x\bm F_1$ であることが分かります。

基本ベクトル †

この考え方を進めるため、$n$ 次元数ベクトルの基本ベクトルというものを定義します。

$i$ 番目の基本ベクトル $\bm e_i$ は、$i$ 番目の要素だけが $1$ で、その他が $0$ であるようなベクトルです。

$\bm e_i= \begin{pmatrix}0\\\vdots\\0\\1\\0\\\vdots\\0\end{pmatrix} \begin{matrix}\\ \\ \\\leftarrow i\\ \\ \\ \end{matrix}$

基本ベクトルに対する出力が分かればすべて分かる †

基本ベクトル $\bm e_i$ に対する出力を $\bm F_i$ としましょう。

$$ \bm F_i = f(\bm e_i) $$

任意のベクトルは基本ベクトルを使って、

$$ \bm a=\begin{pmatrix}a_1\\a_2\\\vdots\\a_n\end{pmatrix}= \sum_1^{i=n} a_i\bm e_i $$

のように展開できるので、$f$ が線形なら

$$ f(\bm a)=f\Big(\sum_1^{i=n} a_i\bm e_i\Big)=\sum_1^{i=n} f(a_i\bm e_i)=\sum_1^{i=n} a_i f(\bm e_i)=\sum_1^{i=n}a_i\bm F_i $$

として求められます。

すなわち、基本ベクトルに対する出力が分かれば任意の入力に対する出力が分かるわけです。

行列 †