線形代数II/基底の変換 の履歴(No.14)
更新- 履歴一覧
- 差分 を表示
- 現在との差分 を表示
- ソース を表示
- 線形代数II/基底の変換 へ行く。
基底の変換†
数ベクトル空間における数ベクトル表現の求め方†
例として、次の3つのベクトルは の基底を為す。
&math( \bm b_1=\begin{pmatrix}1\\0\\0\end{pmatrix}, \bm b_2=\begin{pmatrix}1\\1\\0\end{pmatrix}, \bm b_3=\begin{pmatrix}1\\1\\1\end{pmatrix} );
適当な が与えられたとして、この基底に対する数ベクトル表現 を求めたい。
&math( \bm x=\begin{pmatrix}\bigg.\bm b_1&\bm b_2&\bm b_3\end{pmatrix}\begin{pmatrix}x'\\y'\\z'\end{pmatrix} =B\bm x');
と書けば、 は一次独立なので は正則行列になる。
したがって、 とすれば数ベクトル表現が得られる。
すなわち、
上記の議論は線形独立な任意の3つのベクトル に適用できる。
基底の変換行列†
上の 次元線形空間 に2つの基底を取る
これらの基底に対するベクトル の表現 は、
(1) &math( \bm x=\begin{pmatrix}\bm a_1&\bm a_2&\dots&\bm a_n\end{pmatrix}\bm x_{\comment{widetilde} A} );
(2) &math( \bm x=\begin{pmatrix}\bm b_1&\bm b_2&\dots&\bm b_n\end{pmatrix}\bm x_{\comment{widetilde} B} );
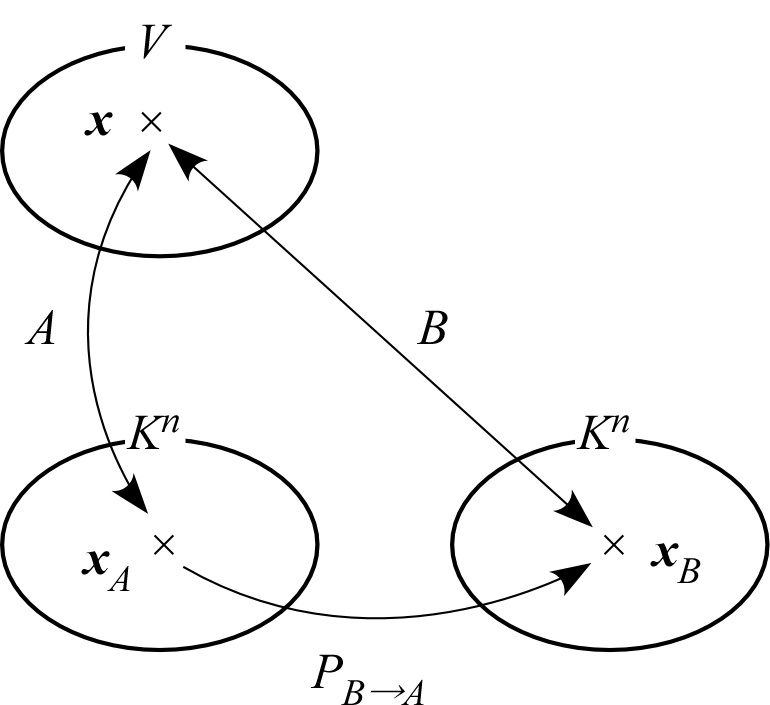
の関係を満たす。図に表わせば、
および はともに 線形写像となるから、その合成写像 も線形写像である。
線形代数I において の線形変換は 行列の積で表せることを学んだ。 すなわち、ある行列 を用いて、
(3)
と表せる。
このとき、 を 基底 から 基底 への基底の変換行列と呼ぶ。
変換の向き†
上記を良く読んで「変換の向きは逆じゃないの?」と思うのは正しい感覚。
どうしてこの向きかというと、
(2) に (3) を代入して、
&math( \bm x=\begin{pmatrix}\bm b_1&\bm b_2&\dots&\bm b_n\end{pmatrix}P_{\comment{widetilde} B\to \comment{widetilde} A}\bm x_{\comment{widetilde} A} );
と (1) とを比べると、
(4) &math( \begin{pmatrix}\bm a_1&\bm a_2&\dots&\bm a_n\end{pmatrix}= \begin{pmatrix}\bm b_1&\bm b_2&\dots&\bm b_n\end{pmatrix}P_{\comment{widetilde} B\to \comment{widetilde} A} );
となり、 の基底ベクトルを並べて右から を掛けることで の基底ベクトルが得られる。
こう書けば変換の向きは正しく思えるはず。
変換行列 $P_{\comment{widetilde} B\to \comment{widetilde} A}$ の具体的な形†
変換行列の列ベクトルを次のように置く。
(4) を列ベクトルごとに見れば、
&math( \bm a_i= \begin{pmatrix}\bm b_1&\bm b_2&\dots&\bm b_n\end{pmatrix}\bm p_i );
一方、 の に対する表現 は
&math( \bm a_i= \begin{pmatrix}\bm b_1&\bm b_2&\dots&\bm b_n\end{pmatrix}\bm a_{i\comment{widetilde} B} );
だったから、
すなわち、
となる。
正則性†
当然、逆写像も線形写像であるから、
であり、
の関係がある。すなわち、基底の変換行列は正則行列である。
例†
に、2つの基底を取る。
&math( \bm a_1=\begin{pmatrix}1\\1\end{pmatrix}, \bm a_2=\begin{pmatrix}1\\-1\end{pmatrix} );
&math( \bm b_1=\begin{pmatrix}1\\2\end{pmatrix}, \bm b_2=\begin{pmatrix}2\\1\end{pmatrix} );
を で展開すれば、
→
→
2つの式をまとめると、
&math( \begin{pmatrix}\bm a_1&\bm a_2\end{pmatrix}&= \begin{pmatrix}\bm b_1&\bm b_2\end{pmatrix} \begin{pmatrix}1/3&-1\\1/3&1\end{pmatrix}\\ &=\begin{pmatrix}\bm b_1&\bm b_2\end{pmatrix} \begin{pmatrix}\bm a_{1B}&\bm a_{2B}\end{pmatrix}\\ &=\begin{pmatrix}\bm b_1&\bm b_2\end{pmatrix}P_{B\to A} );
この表式を用いて、
&math( \bm x&=\begin{pmatrix}\bm a_1&\bm a_2\end{pmatrix}\bm x_A\\ &=\begin{pmatrix}\bm b_1&\bm b_2\end{pmatrix}P_{B\to A}\bm x_A\\ &=\begin{pmatrix}\bm b_1&\bm b_2\end{pmatrix}\bm x_B\\ );
すなわち、
&math( \bm x_B=P_{B\to A}\bm x_A=\begin{pmatrix}1/3&-1\\1/3&1\end{pmatrix}\bm x_A );