線形写像の行列表現と階数 のバックアップ(No.14)

更新

前の単元 ＜＜＜ 　　　　　　　　　　　　　　　線形代数II 　　　　　　　　　　　　　　　＞＞＞ 次の単元

線形写像の行列表現 †

線形写像 T:V\to V' を考える。ただし、 \dim V=n,\dim V'=m

すなわち \forall\bm x\in V に対して \bm y=T(\bm x)\in V'

V の基底 A=\set{ \bm a_1, \bm a_2,\dots,\bm a_n }

V' の基底 B=\set{ \bm b_1, \bm b_2,\dots,\bm b_m }

を考えれば、 \bm x や \bm y の表現を定められる。

\bm x=\begin{pmatrix}\bm a_1&\bm a_2&\dots&\bm a_n\end{pmatrix}\bm x_A

\bm y=\begin{pmatrix}\bm b_1&\bm b_2&\dots&\bm b_m\end{pmatrix}\bm y_B

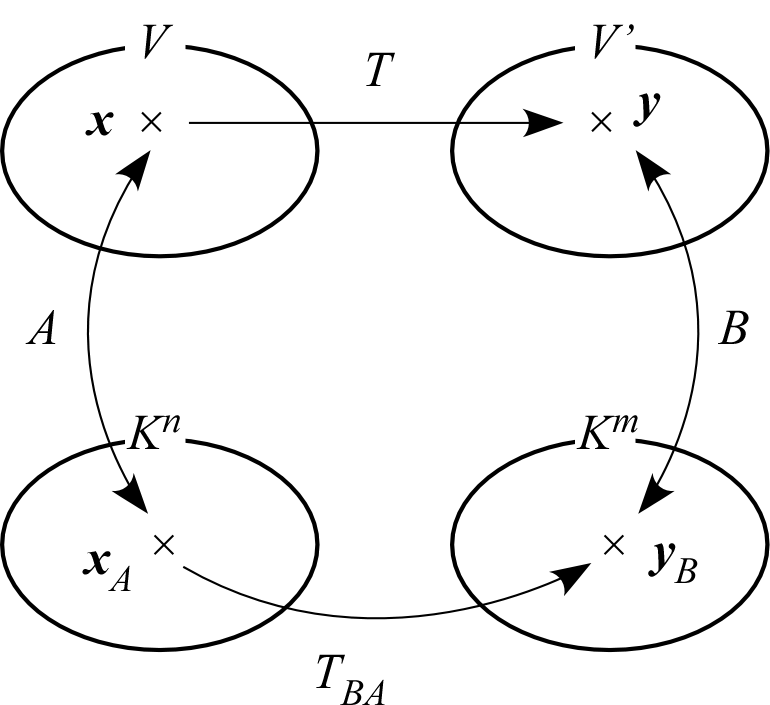
これらの関係は図のようになる。

写像の表現行列.png

\bm x_A\mapsto \bm x 、 \bm x\mapsto \bm y 、 \bm y\mapsto \bm y_B はそれぞれ線形写像なので、 それらの合成写像である \bm x_A\mapsto \bm y_B も線形写像となる。

すなわち、 m\times n 行列 T_{BA} を使って、

\bm y_B=T_{BA}\bm x_A

と表せる。この行列 T_{BA} を、線形写像 T の行列表現と呼ぶ。

$T_{BA}$ の具体的な形 †

T_{BA}=\Big(\bm t_1\ \bm t_2\ \dots\ \bm t_n\Big) と置くと、当然

&math(\bm t_i=T_{BA} \begin{pmatrix}0\\\vdots\\1\\\vdots\\0\end{pmatrix} \begin{matrix}\phantom 0\\\phantom 0\\←\,i\,行目\\\phantom 0\\\phantom 0\end{matrix} );

これと、 T(\bm x)_B=T_{BA}\bm x_A とを比べると、

\bm x_A=\begin{pmatrix}0\\\vdots\\1\\\vdots\\0\end{pmatrix} のとき、 T(\bm x)_B=\bm t

\bm x_A の定義より、

\bm x=\Big(\bm a_1\ \bm a_2\ \dots\ \bm a_n\Big)\bm x_A=\Big(\bm a_1\ \bm a_2\ \dots\ \bm a_n\Big)\begin{pmatrix}0\\\vdots\\1\\\vdots\\0\end{pmatrix}=\bm a_i

だから、

\bm t=T(\bm a_i)_B

すなわち、

&math(T_{BA}= \begin{pmatrix}T(\bm a_1)_B&T(\bm a_2)_B&\dots&T(\bm a_n)_B\end{pmatrix} );

線形写像の行列表現は、
元となる空間の基底ベクトルに線形写像を施して、
先となる空間の基底で表現したものを列ベクトルとする。

基底の変換行列との関係 †

先にやった基底の変換行列 P_{B\to A} は、 上記 T を恒等変換 E に置き換えた形と等しい（ \bm y=\bm x ）

すなわち、 P_{B\to A}=E_{AB}

行列表現の基底変換 †

A から A' および、 B から B' の基底の変換を考える。

\bm y_B=T_{BA}\bm x_A に、 \bm x_A=P_{A\to A'}\bm x_{A'} 、 \bm y_B=P_{B\to B'}\bm y_{B'} を適用すれば、

P_{B\to B'}\bm y_{B'}=T_{BA}P_{A\to A'}\bm x_{A'}

&math( \bm y_{B'}&=T_{B'A'}\bm x_{A'}\\ &=\underbrace{(P_{B\to B'})^{-1}}_{P_{B'\to B}}\ \underbrace{T_{BA}\ \underbrace{(P_{A\to A'})\bm x_{A'}}_{\bm x_A}}_{\bm y_B} );

したがって、

T_{B'A'}=(P_{B\to B'})^{-1}T_{BA}(P_{A\to A'})

基底変換と階数 †

行列の階数は正則行列のかけ算では変化しないことを１年生で学んだ。 すなわち、 P,P' が正則の時、

\rank A=\rank (PA)=\rank(AP')

したがって、線形変換の行列表現の階数も任意の基底変換で保存する。

\rank T=\rank T_{AB}=\rank T_{A'B'}=\rank T_{A''B''}=\dots

基底変換の例 †

T:P^2[x]\to P^1[x] が \bm x\mapsto\frac{d}{dx}\bm x で与えられるものとする。

すなわち、 \bm x=ax^2+bx+c のとき、 T\bm x=2ax+b

これを、 A=\big\{x^2,\ x,\ 1\big\} 、 B=\big\{x,\ 1\big\} を使って表わせば、

&math( \begin{pmatrix}2a\\b\end{pmatrix}=T_{BA} \begin{pmatrix}a\\b\\c\end{pmatrix}); より、 T_{BA}=\begin{pmatrix}2&0&0\\0&1&0\end{pmatrix}

一方、 A'=\big\{x^2+x+1,\ x+1,\ 1\big\} 、 B'=\big\{x+1,\ 1\big\} を使って表わせば、

\bm x=a(x^2+x+1)+b(x+1)+c のとき、
T\bm x&=2ax+a+b\\&=2a(x+1)+(-a+b) より、

&math( \begin{pmatrix}2a\\-a+b\end{pmatrix}=T_{B'A'} \begin{pmatrix}a\\b\\c\end{pmatrix}); より、 T_{B'A'}=\begin{pmatrix}2&0&0\\-1&1&0\end{pmatrix}

また、

\Big(x^2+x+1\ \ x+1\ \ 1\Big)=\Big(x^2\ \ x\ \ 1\Big)P_{A\to A'} より、
P_{A\to A'}=\begin{pmatrix}1&0&0\\1&1&0\\1&1&1\end{pmatrix}

\Big(x+1\ \ 1\Big)=\Big(x\ \ 1\Big)P_{B\to B'} より、
P_{B\to B'}=\begin{pmatrix}1&0\\1&1\end{pmatrix}

これらを用いて、

\left(P_{B\to B'}\right)^{-1}T_{BA}P_{A\to A'}
&math(=\begin{pmatrix}1&0\\1&1\end{pmatrix}^{-1} \begin{pmatrix}2&0&0\\0&1&0\end{pmatrix} \begin{pmatrix}1&0&0\\1&1&0\\1&1&1\end{pmatrix});
&math(=\begin{pmatrix}1&0\\-1&1\end{pmatrix} \begin{pmatrix}2&0&0\\0&1&0\end{pmatrix} \begin{pmatrix}1&0&0\\1&1&0\\1&1&1\end{pmatrix});
&math(=\begin{pmatrix}2&0&0\\-2&1&0\end{pmatrix} \begin{pmatrix}1&0&0\\1&1&0\\1&1&1\end{pmatrix});
=\begin{pmatrix}2&0&0\\-1&1&0\end{pmatrix}
=T_{B'A'}

を確かめられる。

演習 †

T:P^2(x)\to P^2(x) が \bm x\mapsto \frac{d}{dx}\Big\{(x+1)\bm x\Big\} で与えられる。

(1) 上記の基底 A, A' に対する T の表現 T_A=T_{AA} 、 T_{A'}=T_{A'A'} を求めよ

(2) A から A' への変換行列 P_{A\to A'} に対して下記を確かめよ

T_{A'}=\left(P_{A\to A'}\right)^{-1}T_AP_{A\to A'}

線形変換である場合 †

T:V\to V すなわち「線形変換」であるときは B=A なので、このとき T_A=T_{AA} と書けば、

T_{A'}=(P_{A\to A'})^{-1}T_A(P_{A\to A'})

すなわち、 T_A と T_{A'} とは 線形代数I で学んだ「相似」の関係にある。

トレース、行列式、固有値 †

相似な行列 T_A=P_{B\to A}^{-1}T_BP_{B\to A} では、

  • トレース：　　 \tr T_A=\tr T_B
  • 行列式：　　　 \det T_A=\det T_B
  • 階数：　　　　　 \rank T_A=\rank T_B
  • 固有方程式：　 |T_A-\lambda E|=|T_B-\lambda E|=0

が等しくなることを１年生で学んだ。→ 相似変換に対するトレース、行列式、固有値の保存

すなわち線形変換 T を定めれば、基底を指定しなくてもこれらの値が定まることになる。

したがって、線形変換の トレース \tr T 、デターミナント \det T 、 階数 \rank T 、固有値 \lambda_1,\lambda_2,\dots を具体的な基底を与えることなく定義できる。


前の単元 ＜＜＜ 　　　　　　　　　　　　　　　線形代数II 　　　　　　　　　　　　　　　＞＞＞ 次の単元

質問・コメント †




Counter: 33549 (from 2010/06/03), today: 3, yesterday: 0