線形写像の行列表現と階数 のバックアップ(No.8)
更新- バックアップ一覧
- 差分 を表示
- 現在との差分 を表示
- ソース を表示
- 線形代数II/線形写像の行列表現と階数 へ行く。
線形写像の行列表現 †
線形写像 を考える。ただし、
すなわち に対して
の基底
の基底
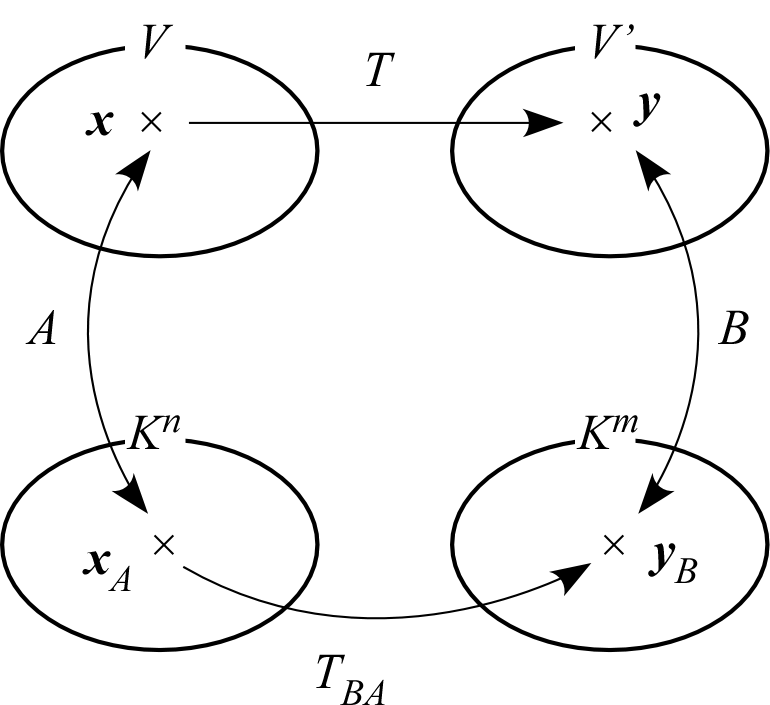
を考えれば、 や の表現を定められ、
これらの関係は図のようになる。
、 、 はそれぞれ線形写像なので、 それらの合成写像である も線形写像となる。
すなわち、 行列 を使って、
と表せる。この行列 を、線形写像 の行列表現と呼ぶ。
$T_{\comment{widetilde}B\comment{widetilde}A}$ の具体的な形 †
基底ベクトル の に対する表現 は、
&math(\bm a_i &=\begin{pmatrix}\bm a_1&\bm a_2&\dots&\bm a_n\end{pmatrix} \begin{pmatrix}0\\\vdots\\1\\\vdots\\0\end{pmatrix}\begin{matrix}\phantom 0\\\phantom 0\\←\,i\,行目\\\phantom 0\\\phantom 0\end{matrix}\\ &=\begin{pmatrix}\bm a_1&\bm a_2&\dots&\bm a_n\end{pmatrix}\bm a_{i\comment{widetilde}A} );
より、
&math( \bm a_{i\comment{widetilde}A} =\begin{pmatrix}0\\\vdots\\1\\\vdots\\0\end{pmatrix}\begin{matrix}\phantom 0\\\phantom 0\\←\,i\,行目\\\phantom 0\\\phantom 0\end{matrix} );
一方、 を で移した は のベクトルなので、その による表現 を考えることができて、 と置けば、
すなわち、
&math(T_{\comment{widetilde}B\comment{widetilde}A}= \begin{pmatrix}T(\bm a_1)_{\comment{widetilde}B}&T(\bm a_2)_{\comment{widetilde}B}&\dots&T(\bm a_n)_{\comment{widetilde}B}\end{pmatrix} );
線形写像の行列表現は、
元となる空間の基底ベクトルを移して、
先となる空間の基底で表現したものを列ベクトルとする。
基底の変換行列との関係 †
先にやった基底の変換行列 は、 上記の を恒等変換 に置き換えた形と等しい( )。
すなわち、
行列表現の基底変換 †
から あるいは から といった基底の変換を考える。
&math( &\bm y_{\comment{widetilde}B}=T_{\comment{widetilde}B\comment{widetilde}A}\bm x_{\comment{widetilde}A}\\ &\phantom{\bm y_{\comment{widetilde}B}}=T_{\comment{widetilde}B\comment{widetilde}A'}\bm x_{\comment{widetilde}A'}\\ &\bm x_{\comment{widetilde}A}=P_{\comment{widetilde}A\to \comment{widetilde}A'}\bm x_{\comment{widetilde}A'} より、\\ &T_{\comment{widetilde}B\comment{widetilde}A'}=T_{\comment{widetilde}B\comment{widetilde}A}P_{\comment{widetilde}A\to \comment{widetilde}A'} ); &math( &\bm y_{\comment{widetilde}B}=T_{\comment{widetilde}B\comment{widetilde}A}\bm x_{\comment{widetilde}A}\\ &\bm y_{\comment{widetilde}B'}=T_{\comment{widetilde}B'\comment{widetilde}A}\bm x_{\comment{widetilde}A}\\ &\bm y_{\comment{widetilde}B}=P_{\comment{widetilde}B\to \comment{widetilde}B'}\bm y_{\comment{widetilde}B'} より、\\ &T_{\comment{widetilde}B'\comment{widetilde}A}=(P_{\comment{widetilde}B\to \comment{widetilde}B'})^{-1}T_{\comment{widetilde}B\comment{widetilde}A} );
両者を合わせると、
特に、 すなわち「線形変換」であるときは、 の基底を定めるだけで行列表現が求まる。 このとき と書けば、
すなわち、 と とは 線形代数I で学んだ 「相似」の関係にあることになる。
と、
&math( \bm y_{\comment{widetilde}A'}&=T_{\comment{widetilde}A'}\bm x_{\comment{widetilde}A'}\\ &=\underbrace{(P_{\comment{widetilde}A\to \comment{widetilde}A'})^{-1}}_{P_{\comment{widetilde}A'\to \comment{widetilde}A}}\ \underbrace{T_{\comment{widetilde}A}\ \underbrace{(P_{\comment{widetilde}A\to \comment{widetilde}A'})\bm x_{\comment{widetilde}A'}}_{\bm x_{\comment{widetilde}A}}}_{\bm y_{\comment{widetilde}A}});
とを見比べて理解したい。
線形写像の階数と行列表現の階数 †
両者は一致するのだが、証明は時間があれば戻って行うこととして、 とりあえず省略。