電磁気学/Faraday の電磁誘導 のバックアップ(No.3)
更新以下、書きかけです。
§1−4 Faraday (ファラデー) の電磁誘導 †
電磁誘導:磁束の変化で「起電力」が生じる
磁束
起電力
すなわち、誘導電流は、
- 磁束の時間変化に比例
- 抵抗に反比例
起電力 = 電位? †
起電力
これは「電位」とは違う?
電位
「電位」ならば一周すればゼロになるはずだが・・・
「電位」は静電場でしか定義されないから、ここでは考えてはいけない。 「動電磁場」では「ベクトルポテンシャル」や「スカラーポテンシャル」の出番。
上記はあくまで「起電力」である。
コイルが無くても †
実はコイルが無くても、いたるところに電場は発生している!
- コイルがなければ抵抗が無限大なので電流は流れない
- コイルがあれば抵抗に応じた電流が流れる
磁束? †
「コイルを貫く磁束」は常に定義可能だろうか?
実は、コイルを表す閉曲線
に対して、
を
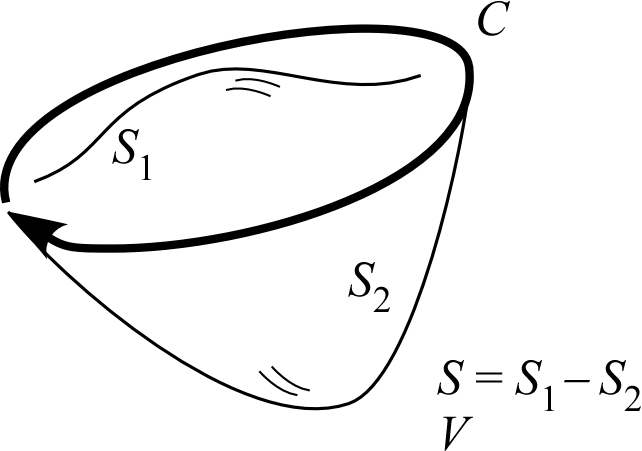
なぜなら、 をつなげた閉曲面 およびその中の体積 を考えれば、
&math( &\int_{S_1}\bm B\cdot\bm ndS-\int_{S_2}\bm B\cdot\bm ndS\\ &=\int_S\bm B\cdot\bm ndS\\ &=\int_V\DIV\bm Bd^3x\\ &=0 );
であるためだ。最後に を用いた。
であるため、磁力線は途中で途切れることなく、常にループを描く。 したがって、もし磁力線が を貫くようであれば、それは必ず も貫くわけである。
以上から、磁束の値は縁の形状 のみにより定義され、磁束を積分する面の取り方に依らないことが分かった。
Faraday の法則(積分形) †
起電力及び磁束を積分で書けば、次式を得る。
&math( \underbrace{\oint_C \bm E\cdot d\bm r}_{\phi}&=-\frac{d}{dt}\underbrace{\int_S\bm B\cdot\bm n dS}_{N} );
Faraday の法則(微分形) †
左辺に Stokes の定理 を適用すれば、
&math( \int_S \rot\bm E\cdot \bm n\,dS&=-\int_S\frac{\PD\bm B}{\PD t}\cdot\bm n dS\\ );
は任意に取れるため、
&math( \rot\bm E=-\frac{\PD\bm B}{\PD t} );
この式を見て、「 を一周積分した起電力が磁束の時間変化に等しい」と読めるように復習しておくこと。