三次元空間での散乱現象
概要†
三次元空間での散乱現象†
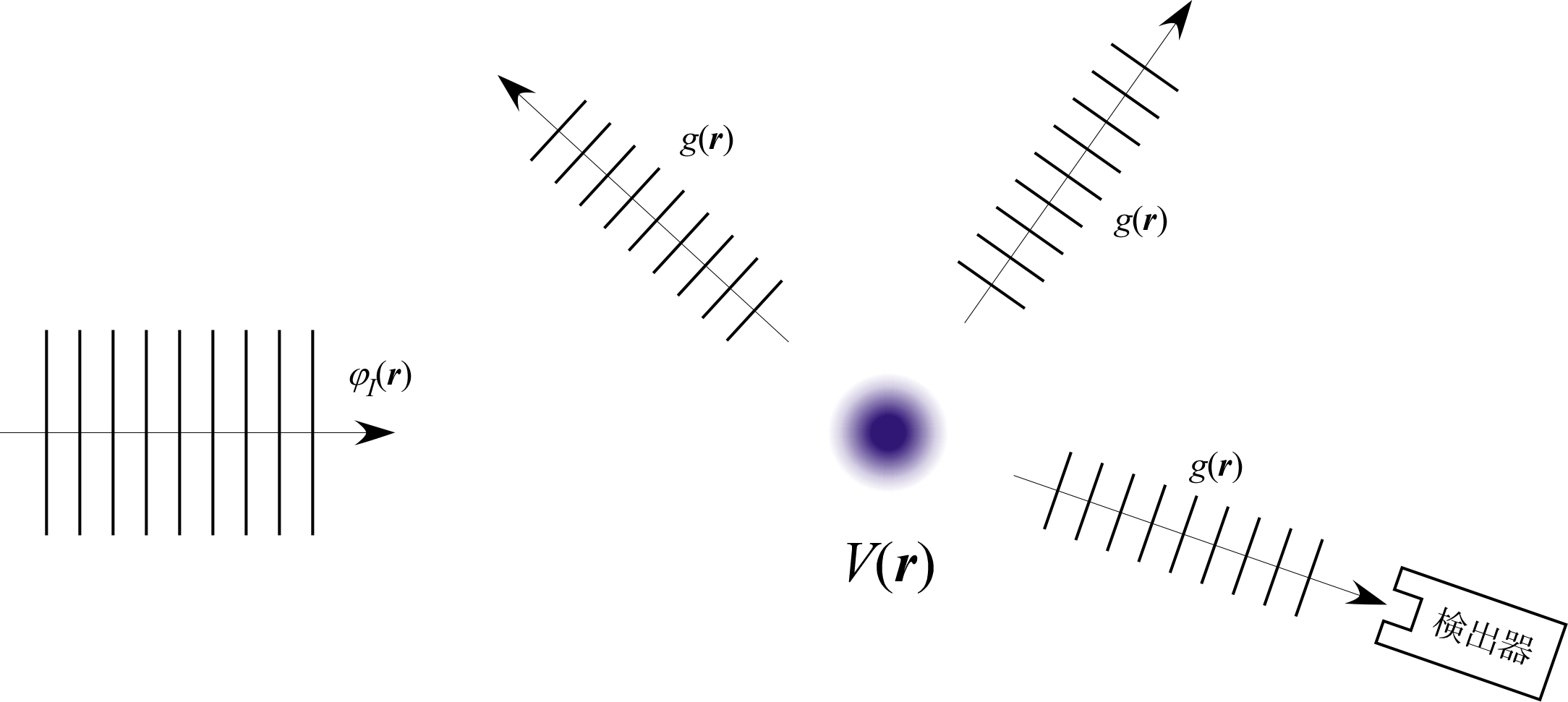
原点で静止した粒子に別の粒子が高速で衝突する過程 (加速器などによる素粒子物理学などに現れる物理現象である)を考える。もし非常に軽い粒子が非常に重い粒子に衝突すると考えられる場合には、原点付近に存在する静的で局所的なポテンシャル $V(\bm r)$ に粒子が入射し、散乱されるという一粒子現象を考えればよいことになる(反跳を無視する近似)。そうでない場合にも、重心座標を用いて2粒子の相対座標で系を記述すれば同様の問題に変換できるため、以下ではそのような系を扱う。
1次元の散乱では、散乱結果について反射波と透過波のみを考えれば良かったが、
3次元の散乱では、はじめに示した図のように散乱波は標的から3次元的に広がる。
この系で我々が最終的に求めたいのは、散乱を受けた入射粒子が原点から見てある角度に構えられた検出器へ入射する確率である。
ポテンシャルが局所的と見なせるとき、遠く離れた位置において粒子は自由である。 入射粒子はそのような遠方において運動量が確定しており、すなわち平面波で表されるとしよう(入射波 $\varphi_I(\bm r)$)。
$$\varphi_I(\bm r)=e^{i\bm k_0\cdot\bm r}$$
1粒子問題では散乱波の振幅は入射波の振幅に比例するから、 1次元の散乱現象の時と同様に、さしあたり入射波の振幅を1として計算しておき 必要に応じて後から振幅をかけることにする。
系の波動関数を入射波 $\varphi_I(\bm r)$ と散乱波 $g(\bm r)$ とに分けて書くことにすると、
$$\varphi(\bm r)=\varphi_I(\bm r)+g(\bm r)$$
このとき原点を向いて構えられた検出器の位置における散乱波の確率流密度 $(\hbar k_0/m)|g(\bm r)|^2$ が散乱実験における検出強度に対応すると考えられる。
数学的には入射波は全空間に広がっているから検出器の位置でも振幅を持つが、 実験的には入射波はビーム状になっているため、ポテンシャル $V(\bm r)$ がゼロではない距離スケールでは平面波と見なせるものの、検出器位置での振幅はゼロと見なせるためである。
定常的な粒子の流れが実現している状況では確率分布が時間によらないから、
$$\left\{-\frac{\hbar^2}{2m}\nabla^2+V(\bm r)\right\}\varphi(\bm r)=\varepsilon\varphi(\bm r)$$
を解いて $g(\bm r)$ を求めることになる。
エネルギーについて†
散乱体から離れた位置では $V(\bm r)=0$ である。
さらに、散乱波は散乱体から四方八方に広がるため、散乱体から十分に離れた箇所では $g(\bm r)\to 0$ も成り立つから、散乱体から十分離れた、入射波のみが存在する領域ではシュレーディンガー方程式は、
$$-\frac{\hbar^2}{2m}{\bm \nabla}^2\varphi_I(\bm r)=\varepsilon\varphi_I(\bm r)\hspace{5mm}\text{すなわち}\hspace{5mm}\Big(\frac{\hbar^2}{2m}\nabla^2+\varepsilon\Big)\varphi_I=0$$
となる。ここから、
$$\varepsilon=\frac{\hbar^2k_0^2}{2m}$$
の関係が得られる。これを代入することで次式を得る。
$$ \frac{\hbar^2}{2m}\Big(\nabla^2+k_0^2\Big)\varphi(\bm r)=V(\bm r)\varphi(\bm r) $$
ボルン近似†
ボルン近似では散乱ポテンシャル $V(\bm r)$ が小さく、 そのため散乱波 $g(\bm r)$ も小さいものとして、 右辺に現れる積 $V(\bm r)g(\bm r)$ を無視する。 当然得られる解は不正確になるが、問題が解きやすくなる。
$$ \frac{\hbar^2}{2m}\Big(\nabla^2+k_0^2\Big) \big\{\underbrace{e^{i\bm k_0\cdot\bm r}\rule[-4pt]{0pt}{0pt}}_{\text{消える}}+g(\bm r)\big\}=V(\bm r)\big\{e^{i\bm k_0\cdot\bm r}+\underbrace{g(\bm r)}_{\text{無視}}\big\} $$
左辺の $e^{i\bm k_0\cdot\bm r}$ に対しては $\nabla^2=-k_0^2$ であるからこの項も消えて、
$$ \frac{\hbar^2}{2m}\Big(\nabla^2+k_0^2\Big)g(\bm r)=V(\bm r)e^{i\bm k_0\cdot\bm r} $$
左辺の $g(\bm r)$ が求めるべき未知の関数、 右辺は既知の関数である。
グリーン関数†
上記のような方程式を解くための便利な方法として、グリーン関数を用いる方法がある。
一般に、ある線形演算子 $\hat L$ と既知の関数 $f(\bm r)$ に対して 次式を満たす $g(\bm r)$ を求める問題を考える。
$$\hat L g(\bm r)=f(\bm r)$$
この方程式は、$\hat L$ は線形であるから、$f(\bm r)=0$ であれば $g(\bm r)=0$ が解となる。 つまり $f(\bm r)$ は $g(\bm r)$ を生じる源となっており、この意味で $f(\bm r)$ をこの方程式のソース (source)と呼ぶことがある。
上記方程式を解くにあたり、もし次式を満たす関数 $G(\bm r)$ (「グリーン関数」*1George Green は19世紀のイギリスの物理学・数学者の名前 → Wikipedia:ジョージ・グリーン(./?%5B%5BWikipedia:%E3%82%B8%E...) と呼ばれる)を適切な境界条件のもとで求められれば、
$$\hat L G(\bm r)=\delta^3(\bm r)=\delta(x)\delta(y)\delta(z)$$
元の方程式の解 $g(\bm r)$ を、
$$g(\bm r)=\iiint f(\bm r')G(\bm r-\bm r') d\bm r'$$
のようにして、任意の $f(\bm r)$ に対して $G(\bm r-\bm r')$ をかけて積分するだけで求められる。 このような手順で微分方程式を解く方法をグリーン関数法と呼ぶ。
この $g(\bm r)$ が元の方程式を満たすことは、
$$\begin{aligned} \hat L g(\bm r)&=\iiint f(\bm r')\hat LG(\bm r-\bm r') d\bm r'\\ &=\iiint f(\bm r')\delta^3(\bm r-\bm r') d\bm r'\\ &=f(\bm r) \end{aligned}$$
と確かめられる。$\hat L$ は $\bm r$ の関数に作用する演算子であるため $\hat L$ に対して $\bm r'$ は定数と見なせることに注意せよ。
電磁気学において、連続分布する電荷の作る電場を、点電荷の作る電場を積分することにより求めたが、 それとまったく同じ考え方である。
散乱現象のグリーン関数†
$|\bm r|=r$ を使って、
$$G(\bm r)=-\frac{1}{4\pi}\frac{e^{ik_0 r}}{r}\hspace{1.5cm}\left(e^{i k_0 r}\ne e^{i\bm k_0\cdot\bm r}に注意せよ\right)$$
と置けば、この関数が
$$ \left(\nabla^2+k_0^2\right)G(\bm r)=\delta^3(\bm r) $$
を満たすことを以下で確かめる。まず、$e^{ik_0r}/r$ が微分可能な点において、すなわち原点以外において、
$$\begin{aligned} \nabla^2\frac{e^{ik_0r}}{r}&=\left(\frac{1}{r}\frac{\partial^2}{\partial r^2}\cancel r+\cancel{\frac{1}{r^2}\hat\Lambda}\right)\frac{e^{ik_0r}}{\cancel r} &=-k_0^2\,\frac{e^{ik_0r}}{r} \end{aligned}$$
したがって、
$$ \left(\nabla^2+k_0^2\right)G(\bm r)=0 $$
であり、この関数がデルタ関数であることと矛盾しない。
後は積分値が正しければ良くて、
$$\begin{aligned} &\iiint_{全空間}\left(\nabla^2+k_0^2\right)\frac{e^{ik_0r}}{r}d\bm r\hspace{3.1cm}(被積分関数は原点以外でゼロ)\\ &=\iiint_V\left(\nabla^2+k_0^2\right)\frac{e^{ik_0r}}{r}d\bm r\hspace{3.2cm}(V\,は原点を中心とする半径\,R\,の微小球内)\\ &=\iiint_V\left(\nabla^2+k_0^2\right)\frac{1}{r}d\bm r\hspace{3.7cm}(r\to 0\,で\,e^{ik_0r}\to 1)\\ &=\iiint_V \bm\nabla\cdot\Big(\bm\nabla\frac{1}{r}\Big)d\bm r {}+\underbrace{\int_0^R \frac{k_0^2}{r}\cdot 4\pi r^2\,dr}_{R\to+0\ \ で\ \to\,0}\hspace{1.1cm}(第2項は\,R\to+0\,でゼロになる)\\[-4mm] &=\int_S \Big(\bm\nabla\frac{1}{r}\Big)\cdot\bm n\,dS \hspace{4.3cm}(ガウスの定理を用いた)\\ &=\int_S -\frac{1}{r^2}\,dS \hspace{5.2cm}(\mathrm{gradient}\,の\,r\,方向成分\ \bm e_{\bm r}\cdot\bm\nabla=\partial/\partial r)\\ &=-\frac{1}{R^2}\cdot 4\pi R^2\hspace{5.cm}(S\,は半径\,R\,の球面)\\ &=-4\pi \end{aligned}$$
したがって、
$$ \left(\nabla^2+k_0^2\right)G(\bm r)=\delta^3(\bm r) $$
が確かめられた。
上述の通り、この $G(\bm r)$ を用いれば、
$$ g(\bm r)=-\frac{1}{4\pi}\frac{2m}{\hbar^2}\iiint\frac{e^{ik_0|\bm r-\bm r'|}}{|\bm r-\bm r'|}V(\bm r')e^{i\bm k_0\cdot\bm r'}d\bm r' $$
と表せる。
散乱源から遠い位置における振幅†
$V(\bm r)$ が原点から近くにしか値を持たず、 その散乱源から遠い個所での振幅を求める場合には、 上記の積分内で $r'\ll r$ を仮定してよいから、
$$\begin{aligned} |\bm r-\bm r'|=&\sqrt{(\bm r-\bm r')\cdot(\bm r-\bm r')}\\ =&\,\sqrt{r^2-2\bm r\cdot\bm r'+r'^2}\\ =&\,r\sqrt{1-\frac{2\bm r\cdot\bm r'}{r^2}-\cancel{\frac{r'^2}{r^2}}}\\ \simeq&\,r\left(1-\frac{\bm r\cdot\bm r'}{r^2}\right)\\ \end{aligned}$$
$$ ik_0|\bm r-\bm r'|\simeq ik_0\big\{r-(\bm r/r)\cdot\bm r'\big\} $$
$$ \frac{1}{|\bm r-\bm r'|}\simeq \frac{1}{r}\left(1+\frac{\bm r\cdot\bm r'}{r^2}\right)\simeq\frac{1}{r}\\ $$
として、
$$\begin{aligned} g(\bm r)=&-\frac{1}{4\pi}\frac{2m}{\hbar^2}\iiint{\color{red}\frac{e^{ik_0\{r-(\bm r/r)\cdot\bm r'\}}}{r}}V(\bm r')e^{i\bm k_0\cdot\bm r'}d\bm r'\\ =&-\frac{1}{4\pi}\frac{2m}{\hbar^2}\underbrace{\frac{e^{ik_0 r}}{r}}_{rに依存}\underbrace{\iiint V(\bm r')e^{ik_0(\bm k_0/k_0-\bm r/r)\cdot\bm r'}d\bm r'}_{方向\bm r/rのみに依存} \end{aligned}$$
のように、$\bm r$ の大きさ $r$ に依存する部分と方向 $\bm r/r$ に依存する部分とを分離できる。*2大きさが $\bm k_0$ に等しく、$\bm r$ の方向を向く波数ベクトル $\bm k'=k_0 (\bm r/r)$ を導入すれば、$g(\bm r)=-\frac{1}{4\pi}\frac{2m}{\hbar^2}\frac{e^{i\bm k'\cdot\bm r}}{r}\iiint V(\bm r')e^{i(\bm k_0-\bm k')\cdot\bm r'}d\bm r'$ とも書ける。
散乱問題では入射波方向 $\bm k_0$ を軸に、散乱方向 $\bm r$ を球座標を用いて表すのが一般的である。
このとき、$\theta,\phi$ はそのまま「散乱角」を表して、上式より $g(\bm r)$ は
$$ g(\bm r)=g(r,\theta,\phi)=\frac{e^{ik_0 r}}{r}f(\theta,\phi) $$
と書けることになる。 つまり、$g(r,\theta,\phi)$ の $r$ 依存性は $V$ に依存しない。
散乱断面積†
$e^{ik_0 r}/r$ は原点から $1/r$ で減衰しながら等方的に広がる球面波である。$1/r$ の係数は絶対値の二乗が $1/r^2$ に比例して減衰することを意味しており、 距離とともに波が広がることによる減衰を表している。(確率流密度が $1/r^2$ に比例するとき、立体角 $d\Omega$ あたりの表面積 $r^2d\Omega$ を掛けた値が $r$ によらず一定になる)
したがって散乱波 $g(\bm r)$ も、$f(\theta,\phi)$ を一定とみなせる狭い角度範囲 $d\theta,d\phi$ だけ見れば散乱体から遠い位置において波数 $k_0$ の球面波のように振る舞う。 そして $f(\theta,\phi)$ はそれぞれの角度範囲の球面波の振幅および位相の散乱角依存性を表している。
位置 $r,\theta,\phi$ における単位面積・単位時間あたりの流量(= ベクトル量である)の $r$ 方向成分は、
$$\begin{aligned} S_{g,r} &=\mathrm{Re}\left[g^*(r,\theta,\phi)\frac{\hbar}{im}\frac{\partial}{\partial r}g(r,\theta,\phi)\right]\hspace{1.2cm}(\bm e_{\bm r}\cdot\bm\nabla=\partial/\partial r)\\ &=\mathrm{Re}\left[\frac{\hbar}{im}\frac{1}{r}\left(-\cancel{\frac{1}{r^2}}+\frac{ik_0}{r}\right)|f(\theta,\phi)|^2\right]\hspace{0.5cm}(1/r^2\,の項は虚部になる)\\ &=\frac{\hbar k_0}{mr^2}|f(\theta,\phi)|^2\\ &=\frac{S_I}{r^2}|f(\theta,\phi)|^2\hspace{4.1cm}(S_I=\hbar k_0/m は入射波の流量)\\ \end{aligned}$$
である。これが位置 $r,\theta,\phi$ に置かれた検出器で検出される単位面積あたり、単位時間あたりの粒子の検出確率に相当する。*3波動関数は入射波と散乱波の重ね合わせであるため、数学的には入射波も検出器に入ってしまうが、実際の系では検出器は入射平面波の当たらない箇所に置かれる
この流量を半径 $r$ の球面 $S$ 上で積分すると、
$$\begin{aligned} I_g &=\int_S \bm S_g\cdot\bm n \,dS\\ &=\int_S S_{g,r} \,dS\\ &=\iint\frac{S_I}{\cancel{r^2}}|f(\theta,\phi)|^2\cdot\cancel{r^2}\sin\theta\,d\phi\,d\theta\\ &=S_I\cdot \underbrace{\iint|f(\theta,\phi)|^2\sin\theta\,d\phi\,d\theta}_{\sigma^\mathrm{total}}\\ \end{aligned}$$
のように $r$ によらない定数となり、 これが散乱波全体の単位時間あたりの流量である。
$S_I$ は入射波の単位時間、単位面積あたりの流量であるから、 $\sigma^\mathrm{total}$ は面積の次元を持ち、「散乱断面積」と呼ばれる。
空間的に一様な密度を持つ平面波として入射する波のうち、この面積に当たった分に相当する流量だけが散乱波となったと解釈するのである。
また、$\sigma^\mathrm{total}$ の積分内の関数
$$ \sigma(\theta,\phi)=|f(\theta,\phi)|^2 =\left(\frac{m}{2\pi\hbar^2}\right)^2\left|\iiint V(\bm r')e^{ik_0(\bm k_0/k_0-\bm r/r)\cdot\bm r'}d\bm r'\right|^2 $$
は「微分散乱断面積」あるいは単に「微分断面積」と呼ばれる。 微分散乱断面積を立体角 $d\Omega=\sin\theta\,d\phi\,d\theta$ で積分したものが散乱断面積となるわけだ。
確率密度の保存は?†
1次元の散乱問題では 反射波と透過波の流量を加えると入射波の流量と等しかった。
上で考えた3次元の散乱問題では入射波は全空間に広がる平面波であり、そのまま透過波にもなる。 すなわち、入射波がすべて透過するにもかかわらず散乱波が生じる???
- 散乱波はどこから来たのか?
- 散乱により入射波は減衰しないのか?
実のところ、散乱による入射波の減衰は $g(\bm r)$ に含まれている。
すなわち、$g(\bm r)$ はいわゆる散乱波を表すだけでなく、 散乱を生じたことによる入射波の変化分も含んでいるのである。 $g(\bm r)$ が $\varphi_I$ と反対の複素位相を持てば 互いに打ち消しあって振幅が小さくなることに注意せよ。
上では原点を中心とする球面上で $g(\bm r)$ のわき出し量を計算したが、 $\varphi(\bm r)=\varphi_I(\bm r)+g(\bm r)$ について近似を用いず正確な湧き出し量を求めれば、 その結果はゼロとなる。これが3次元の散乱問題における確率密度の保存である。
以前見た通り、ボルン近似をする前であれば確率の保存が厳密に成り立つことは シュレーディンガー方程式から保証されている。 一方で、ボルン近似後の解については確率が保存されないのではないかと思われるが、 個人的には未確認なので、今後調べたい。
ラザフォード散乱†
ラザフォードは重い原子に $\alpha$ 線(ヘリウム $Z=2$ の原子核)を入射する散乱実験を行い、そこから原子半径に比べて原子核の半径がけた違いに小さいことを示し、その結果をもとに惑星型原子モデルを提唱した。ラザフォードはこのとき古典的な理論により実験結果を解析したが、ここでは同様の問題を上記の知識を生かして量子論的に扱おう。
このとき原子核同士の相互作用はクーロン相互作用そのものを使って構わない。 というのも、原子核の周りにいる電子によって原子核からの電場が遮蔽される効果は、高速でぶつかる2つの原子核が相互作用するようなごく短距離(原子核サイズの距離スケール)では無視できるためだ。(電子自身は軽すぎてヘリウム原子核の軌道を変えられない)
$$V(\bm r)=\frac{1}{4\pi\epsilon_0}\frac{qq'}{r}$$
とはいえ実は、厳密なクーロンポテンシャルを使ってしまうと計算上発散が現れ困難が生じるため、ここでは距離スケール $r_0$ で遮蔽されたクーロンポテンシャル
$$V(\bm r)=C\frac{e^{-r/r_0}}{r}$$
に対して計算を行い($C=qq'/4\pi\epsilon_0$)、最後に $r_0\to \infty$ の極限を考えることにより、「ほぼ完全なクーロン相互作用」に対する散乱を調べることにする。
詳細は省くが、上式に代入し積分すると次式を得る。
$$ f(\theta,\phi)=-\frac{mC}{2\hbar^2k_0^2}\frac{(2k_0r_0)^2}{1+(2k_0r_0)^2\sin^2\theta/2} $$
ここで、物質波の波長 $2\pi/k_0$ に比べて遮蔽長 $r_0$ が小さいとき、 すなわち $2k_0r_0\ll 1$ が成り立つとき、分母の $1$ に比べて $\sin$ の項が無視できて、$f(\theta,\phi)$ は定数となる。 これは散乱波が等方的になることを意味するが、このときデルタ関数による散乱、 グリーン関数がそのまま解として表れていることに注意せよ。 これは、遮蔽長(ポテンシャルが届く距離)が非常に短ければ、実質的にデルタ関数と変わらなくなる、と理解できる。
逆に遮蔽長が長く $r_0\to\infty$ となるときには、$2k_0r_0\to\infty$ であり、$f(\theta,\phi)$ は $\theta\to 0$ で発散する。
見やすくするために $\displaystyle\frac{1}{1+A^2\sin^2\theta/2}$ の部分だけ取り出して、 角度依存性をプロットしたのが下図である。
$A=2k_0r_0$ が小さいときにはほぼ等方的であるが、大きくなるにしたがって、 すなわち遮蔽長 $r_0$ が波長 $2\pi/k_0$ に比べて大きくなるに従って、 $|f(\theta,\phi)|$ も $\sigma(\theta,\phi)=|f(\theta,\phi)|^2$ も $\theta\sim 0$ 方向に偏っていくことが分かる。
- $\theta=0$ での値を $f=-\frac{mC}{2\hbar^2k_0^2}(2k_0r_0)^2=f_0$ と置くと、この値は $r_0\to\infty$ で発散する
- $\theta=\pi$ では $f=\frac{f_0}{1+(2k_0r_0)^2}$ となり、$r_0\to\infty$ で有限値 $-mC/2\hbar^2k_0^2$ をとる
- つまり $r_0\gg 2\pi/k_0$ では $\theta\sim 0$ への散乱が非常に大きくなるものの、それ以外の方向にも散乱波は出る
- ラザフォード散乱では $C>0$ なので $\theta\sim 0$ において符号は負、入射波と打ち消しあう符号を持つ
- 散乱された波は $\theta=0$ に近い角度に多く検出される
- それ以外の方向にも検出されないわけではない($f(\theta=\pi)$ は $r_0\to\infty$ でも有限値 $-mC/2\hbar^2k_0^2$ だけある)
上で議論したとおり、$C>0$ の場合には $g(\bm r)$ により入射波の減衰が表されていることが確認できた。 これは上図のように粒子同士に反発力が働く場合に対応する。
一方で、$C<0$ つまり2つの粒子の間に引力的な相互作用が働く場合には、 前方散乱により透過波はむしろ入射波よりも強められることになる。 これは、下図のように理解できて、散乱されたからと言って $\theta=0$ 方向への透過波が 必ずしも減衰せず、むしろ強められることもあることが分かる。
古典論との対応†
教科書では、$C=\frac{qq'}{4\pi\epsilon_0},\hbar k_0=mv_0, r_0\to \infty$ とした量子論の結果
$$ \sigma(\theta,\phi)=\frac{1}{4}\left(\frac{qq'}{4\pi\epsilon_0mv_0^2}\right)^2\frac{1}{\sin^4(\theta/2)} $$
と、古典論で得られる
$$ \sigma(\theta,\phi)=\frac{1}{4}\left(\frac{qq'}{4\pi\epsilon_0mv_0^2}\right)^2\frac{1}{\sin^4(\theta/2)} $$
とが完全に一致する、めでたしめでたし、としているが、これらの解が見た目上一致していることの解釈には注意が必要である。
古典論の解†
古典論では入射波はすべて散乱波となる。 そのため、散乱体の後ろには「影」ができて、そこには粒子は到達しない。
系の特性長を $\frac{qq'}{4\pi\epsilon_0mv_0^2}=1$ と置いて、 原点に置いた散乱体による散乱の様子をプロットした。
散乱体の近くを通る粒子ほど大きく散乱され、 遠くを通る粒子はほとんど影響を受けずほぼまっすぐ通過する。
微分散乱断面積が $\theta=0$ で発散するのは、 原子から遠く離れた位置に入射する絶対的多数の粒子が、 原子のポテンシャルをほとんど受けず、ほぼ直進することに対応する。
ただし、厳密に $\theta=0$ となる粒子は存在しないので、 $\sigma$ が $\theta=0$ で発散するというのは、 $\lim_{\theta\to 0}\sigma=\infty$ という意味であり、 $\sigma(\theta=0)$ は本来はゼロである。
量子論の解の怪?†
一方、量子論で求めた解では、原子との相互作用により散乱波が生じるものの、 入射波自体は散乱源を素通りする。
素通りした入射波はどうなるかというと、上記で見た通り $\theta=0$ の散乱波と打消し合って $x$ 軸上では振幅が減る・・・と思いきや、 実は遮蔽のない厳密なクーロンポテンシャルに対する解を使ってそのまま計算してしまうと $\theta=0$ で $f(\theta,\phi)$ は発散するので、 入射波に比べてむしろ散乱波が極端に大きくなって、 むしろ散乱波のせいで散乱体の後ろで確率密度が無限大になる。
影になるはずの部分でむしろ粒子密度が上がっており、 そればかりか無限大にまでなっているのは明らかにおかしい。
思い出すべきこととして、上記の計算には散乱波を「十分遠方」で観測するという近似が入っていた。 散乱波は距離とともに減衰するので、$\theta\ne 0$ だったり、$r_0$ が有限だったりすれば、遠いところで散乱波の振幅が小さくなり、問題が無くなる。
ただし微分断面積が無限大になってしまうと、無限大を何分の一にしてもやはり無限大で、らちがあかない。
古典論で見た $\theta=0$ の粒子は散乱体から遠いところを通過する粒子であったのに対して、 量子論での散乱波は常に原点から発生するのだから、様子が大きく異なるのも頷ける。 $\theta\ne 0$ では散乱波は徐々に $x$ 軸から離れていき、 十分遠方では古典論との差は無くなる。でも、$\theta=0$ はダメだ。
有限の遮蔽がかかっている限り、$\theta=0$ の散乱波も振幅は有限であるから、 散乱波は距離とともに減衰して、散乱体から十分遠く離れた位置では入射波を減衰させるように作用する。
さらに遠くでは散乱波が減衰しきって、入射波がほとんどそのまま透過波として観測される。
量子論の解で散乱体の後ろの影が距離とともにぼやけて消えていくのは、 本来影であるべき部分に物質波が回折して回り込むためだ。 つまり、散乱体の直後では波の振幅が少し減るものの、遠く離れると影が薄くなるのは量子論の効果と言える。
このように見ると、式の上では一致した古典論の解と量子論の解とでは、 その実態が大きく異なることが理解できる。
また、有限の遮蔽で計算した結果は良いとして、 遮蔽を完全にゼロにした量子力学的な解については、 実は正しい解を与えていないのではないかとも思われる。
これは、 「ポテンシャルがゼロと見なせるほど散乱体から離れた箇所からさらに十分離れた箇所で観察する」 という「遠方近似」に対して、$1/r$ でしか減衰しないクーロンポテンシャルではどれだけ離れても ポテンシャルをゼロと見なせないことが制約になっているのだろう。
遠方近似する前の式は次のような形をしていたが、
$$ g(\bm r)=-\frac{1}{4\pi}\frac{2m}{\hbar^2}\iiint\frac{e^{ik_0|\bm r-\bm r'|}}{|\bm r-\bm r'|}\underbrace{V(\bm r')}_{\propto\, 1/r'}e^{i\bm k_0\cdot\bm r'}d\bm r' $$
$V(r')\propto 1/r'$ では、積分中に $\displaystyle\frac{1}{|\bm r-\bm r'|}\frac{1}{|\bm r'|}$ の形が現れる。この形は原点付近($|\bm r'|\ll|\bm r|$)に於いて
$$\sim\frac{1}{|\bm r|}\frac{1}{|\bm r'|}$$
となるのに対して、$\bm r$ 付近($|\delta\bm r|=|\bm r-\bm r'|\ll|\bm r|$)に於いて
$$\sim\frac{1}{|\delta\bm r|}\frac{1}{|\bm r|}$$
となるから、どんなに $r$ が大きかったとしても、 両者は同程度の寄与を持ってしまい、遠方近似が成立しないのだ。
現実的にも、遮蔽ゼロの散乱体の散乱断面積は無限大なので、 散乱波を観測するには入射ビームの直径も無限大に取らなければならない。 入射ビーム径が有限の場合の解は、同程度の遮蔽長に対して計算した解と近い形になるはずで、 遮蔽ゼロの結果に現実的な物理的意味があるとは思えない。
有限の遮蔽がある場合、入射波と散乱波を合わせた全波動関数に対する確率密度 $|\phi|^2=|\phi_I+g|^2$ をプロットすれば次図のようになり、 入射波と散乱波との干渉により振幅が波打つことを除いて、 古典論の予想と良い一致を示す。
$b_0=1,2k_0r_0=10$ 等高線は $f(\theta,\phi)$ 一定の箇所を表す。
- 中央の白い部分は遠方近似が成り立たず、 入射波より散乱波が大きくなっている物理的に意味の無い領域。
- そこを越えると散乱波が入射波を打ち消して散乱体が「影」を作っている様子が見られる。
- さらに右へ行くと回折により影が徐々に薄くなっていく。これは量子的な解に特有の現象。
- 影の周囲は散乱波が重ね合わされて周囲よりも密度が上がっている。これは古典論の予想と合う。
- 影の部分の左側に確率密度が波打つ定在波が見られるが、これも入射波と散乱波の干渉による、量子論に特有なもの。
まとめ†
遮蔽のないラザフォード散乱の解は $\theta\sim 0$ 付近では現実的ではない振る舞いをする。とはいえ、$\theta\ne 0$ では遮蔽の緩い場合と遮蔽のない場合との差はほとんど無いため、 ある程度大きな $\theta$ に対して計算する際には遮蔽のない式を用いても問題はない。
質問・コメント†
確率密度の保存についての質問†
F.M ()
「g(r)が散乱波を表すだけでなく、 散乱を生じたことによる入射波の変化分も含んでいる」というところがよくわかりません。散乱波の確率密度が負になるような気がしてしまうのですが...
(確率密度に関しての正確な知識を持ち合わせていないためにこのような疑問が湧いてしまったのかもしれません)
- 系の波動関数はあくまで $\varphi$ であり、これを問題を解くために便宜的に $\varphi=\varphi_I+g$ と分けたに過ぎない点を確認して下さい。$\varphi_I$ は入射波そのものです。散乱によって生じる入射波からのズレ(入射波の減衰と散乱)はすべて $g$ に含まれることになります。そして全体の確率密度は $|\varphi|^2=|\varphi_I+g|^2$ ですので、$g$ は $\varphi_I$ と強め合うこともあれば、弱め合うことも考えられるという点を考えると、「散乱波の確率密度が負」という結論にいたらずに済むのではないかと思います。 -- 武内(管理人)
- 解決しました。ありがとうございます。 -- F.M
*1 George Green は19世紀のイギリスの物理学・数学者の名前 → Wikipedia:ジョージ・グリーン
*2 大きさが $\bm k_0$ に等しく、$\bm r$ の方向を向く波数ベクトル $\bm k'=k_0 (\bm r/r)$ を導入すれば、$g(\bm r)=-\frac{1}{4\pi}\frac{2m}{\hbar^2}\frac{e^{i\bm k'\cdot\bm r}}{r}\iiint V(\bm r')e^{i(\bm k_0-\bm k')\cdot\bm r'}d\bm r'$ とも書ける。
*3 波動関数は入射波と散乱波の重ね合わせであるため、数学的には入射波も検出器に入ってしまうが、実際の系では検出器は入射平面波の当たらない箇所に置かれる
添付ファイル: