バンド理論の勉強
目次†
若林克法先生の授業のノートをもとに勉強しなおす†
2015-02-24~26 に、当時 NIMS にいらした若林克法先生 (現在は関西学院大学) が 筑波大学でグラフェンの特異なナノスケール効果について授業をしてくださいました。
その際のノートなどを見ながら、バンド理論について勉強しなおそうと思います。
2020-02-19~21 に再び若林克法先生がいらっしゃり授業をしてくださった。 今回はちゃんと授業を受けられたので、その内容を元に内容に手を入れています。
いずれにしても、勉強不足の私が四苦八苦して理解できたかどうかギリギリのところを まとめていますので、間違いも多いかもしれません。ご容赦ください。
原子軌道の線形結合により分子軌道を構成(LCAO法の基礎)†
wikipedia:LCAO法 などに紹介されている、広い分野で利用されている方法です。
水素原子 H = 原子軌道†
水素原子では1つの陽子の周りを1つの電子が回っている。この電子に対する時間を含まないシュレーディンガー方程式は、
$$\left\{-\frac{\hbar^2}{2m}\nabla^2-\frac{e^2}{r}\right\}\phi(\bm r)=\varepsilon\phi(\bm r)$$
これを解いた基底状態は $1s$ 軌道と呼ばれる。
基底状態のエネルギーを$\varepsilon_{1s}$
固有関数を$\phi_{1s}(\bm r)$としよう。
水素分子 H2 = 分子軌道†
陽子が2つあるとき、その周辺での「電子1つに対する」ハミルトニアンは、
$$\hat H=\frac{-\hbar^2}{2m}\nabla^2-\frac{e^2}{r_1}-\frac{e^2}{r_2}$$
ただし、$r_1, r_2$ はそれぞれの陽子からの距離、となる。
それぞれの陽子を中心とした2つの 1s 軌道の波動関数を元にして、 それらの線形結合によりこの「分子軌道」を近似的に表したい。
$$\Phi(\bm r)=c_1\phi_1(\bm r)+c_2\phi_2(\bm r)$$
原子軌道(AO: atomic orbital) の線形結合(LC: linear combination) で近似するので LCAO 近似と呼ばれる。
陽子2つに電子1つなので、正確には水素分子ではなく水素分子イオン H2+ を考えていることになる。 最終的に「分子」にするにはエネルギーの低いほうから順に電子を詰める。つまり電子・電子間の相互作用は考えない。
ものすごく大雑把な近似†
$\phi_1(\bm r)$ は陽子 1 の周り以外でほぼゼロになると考えて、
$$-\frac{e^2}{r_2}\times\phi_1(\bm r)=0$$
と近似すれば、
$$\hat H\phi_1(\bm r)=\varepsilon_{1s}\phi_1(\bm r)$$
同様に、
$$\hat H\phi_2(\bm r)=\varepsilon_{1s}\phi_2(\bm r)$$
とすれば、任意の $c_1,c_2$ に対して
$$\hat H\Phi(\bm r)=\varepsilon_{1s}\Phi(\bm r)$$
となって、$\Phi(\bm r)$ はエネルギー $\varepsilon_{1s}$ を持つ固有状態となる。
これは2つの原子が遠く離れて別々に置かれており、 陽子1の周りに $|c_1|^2$ の確率で、 陽子2の周りに $|c_2|^2$ の確率で、電子が見出される状態に対応する。
ヒュッケル法†
$\phi_1(\bm r)$ にある電子に対する陽子2からのポテンシャルが完全には無視できない場合にも、 $\phi_1,\phi_2$ の重なりが小さい場合には $c_1,c_2$ を適切に選ぶことで $\Phi$ は近似的に $\hat H$ の固有関数となる。
$\Phi(\bm r)=c_1\phi_1(\bm r)+c_2\phi_2(\bm r)$ を $\ket\Phi=c_1\ket 1+c_2\ket 2$ と書くことにする。
$\hat H\ket\Phi=E\ket\Phi$ となるように $c_1,c_2$ を決めるため、左から $\bra 1$ をかけてみる。
$$c_1\underbrace{\bra 1\hat H\ket 1}_{h_{11}}+c_2\underbrace{\bra 1\hat H\ket 2}_{h_{12}}= c_1E\underbrace{\braket{1}{1}}_{=\,1}+c_2E\underbrace{\braket{1}{2}}_{=\,\delta}$$
ここで、 $|\delta|\ll 1$ つまり $\phi_1,\phi_2$ の重なり積分 $\delta=\braket{1}{2}$ が十分に小さいとして無視すると(これを wikipedia:ヒュッケル法 と呼ぶ)、
$ \begin{cases} c_1h_{11}+c_2h_{12}=c_1E\\ c_1h_{21}+c_2h_{22}=c_2E\\ \end{cases} $ つまり $ \begin{pmatrix} h_{11}&h_{12}\\ h_{21}&h_{12}\\ \end{pmatrix}\begin{pmatrix}c_1\\c_2\end{pmatrix}= E\begin{pmatrix}c_1\\c_2\end{pmatrix} $
を得る。(2行目の式は左から $\bra 2$ をかけて得た)
$$h_{12}=\bra 1\hat H\ket 2=\big(\bra 2\hat H^\dagger\ket 1\big)^\dagger=\big(\bra 2\hat H\ket 1\big)^*=h_{21}^*$$
より左辺の行列はエルミートであり、実数固有値と正規直交固有ベクトルを持つ。
$h_{11},h_{22}$ について†
$$ \begin{aligned} h_{11}&=\braketm{1}{\hat H}{1}\\ &=\int d\bm r\phi_1^*(\bm r)\left[-\frac{\hbar^2}{2m}\nabla^2-\frac{e^2}{r_1}-\frac{e^2}{r_2}\right]\phi_1(\bm r)\\ &=\underbrace{\int d\bm r\phi_1^*(\bm r)\left[-\frac{\hbar^2}{2m}\nabla^2-\frac{e^2}{r_1}\right]\phi_1(\bm r)}_{\displaystyle \varepsilon_{1s}} {}-\underbrace{\int d\bm r\phi_1^*(\bm r)\frac{e^2}{r_2}\phi_1(\bm r)}_{\displaystyle \tilde\alpha}\\ &=\varepsilon_{1s}-\tilde\alpha\equiv-\alpha \end{aligned} $$
同様にして $h_{22}=-\alpha$ となる。
$h_{21},h_{12}$ について†
$$ \begin{aligned} h_{21}&=\braketm{2}{\hat H}{1}\\ &=\int d\bm r\phi_2^*(\bm r)\left[-\frac{\hbar^2}{2m}\nabla^2-\frac{e^2}{r_1}-\frac{e^2}{r_2}\right]\phi_1(\bm r)\\ &=\int d\bm r\phi_2^*(\bm r)\varepsilon_1\phi_1(\bm r) {}-\underbrace{\int d\bm r\phi_2^*(\bm r)\frac{e^2}{r_2}\phi_1(\bm r)}_{\displaystyle \gamma}\\ &=\varepsilon_1\underbrace{\braket{2}{1}}_{=\,\delta\ \sim\,0}-\gamma=-\gamma \end{aligned} $$
時間によらない波動関数は必ず実数関数に取れる。$\phi_1,\phi_2$ が実数関数であるとき、$\gamma$ は実数になるため、以降では $\gamma\in\mathbb R$ とする。
このとき、$h_{12}=h_{21}^*=h_{21}=-\gamma$
$c_1,c_2$ を求める†
$$ \begin{pmatrix} \alpha-E&-\gamma\\ {}-\gamma&\alpha-E \end{pmatrix}\begin{pmatrix}c_1\\c_2\end{pmatrix}=\bm 0 $$
より、自明でない解を持つためには
$$ \begin{vmatrix} {}-\alpha-E&-\gamma\\ {}-\gamma&-\alpha-E \end{vmatrix}=(\alpha-E)^2-\gamma^2=0 $$
したがって、
$$E=-\alpha\pm\gamma$$
$E=-\alpha+\gamma$ のとき、$\begin{pmatrix}c_1\\c_2\end{pmatrix}=\frac{1}{\sqrt 2}\begin{pmatrix}1\\-1\end{pmatrix}$
$E=-\alpha-\gamma$ のとき、$\begin{pmatrix}c_1\\c_2\end{pmatrix}=\frac{1}{\sqrt 2}\begin{pmatrix}1\\1\end{pmatrix}$
つまり、
$\Phi\propto\phi_1-\phi_2$ のとき、エネルギーは $E=\epsilon_{1s}-\tilde\alpha+\gamma$ (反結合性軌道)
$\Phi\propto\phi_1+\phi_2$ のとき、エネルギーは $E=\epsilon_{1s}-\tilde\alpha-\gamma$ (結合性軌道)
である。
結合性軌道は反結合性軌道に比べ、両方の陽子からの引力相互作用を受ける 分子中心付近での状態密度が高いため、 $\braketm{1}{\hat H}{2}$ の分だけエネルギーが低くなっている。
ヒュッケル近似の意味†
波動関数は重ならないが($\braket{1}{2}=0$)
相互作用は取り入れる($\braketm{1}{\,e^2/r\,}{2}\ne 0$)
という近似が必要になる意味があまり良く理解できていない。。。
このあたりを理解するために、重なり積分をゼロとせずに、もう少しまじめに考えた結果と比べてみる。
$\braket{1}{2}=\braket{2}{1}=\delta\ne 0$ とすると、
$$ \begin{pmatrix} \varepsilon_{1s}-\tilde\alpha&\varepsilon_{1s}\delta-\gamma\\ \varepsilon_{1s}\delta-\gamma&\varepsilon_{1s}-\tilde\alpha\\ \end{pmatrix}\begin{pmatrix}c_1\\c_2\end{pmatrix}= \begin{pmatrix} E&E\delta\\ E\delta&E\\ \end{pmatrix}\begin{pmatrix}c_1\\c_2\end{pmatrix} $$
これが自明でない解を持つには、
$$ \begin{vmatrix} \varepsilon_{1s}-E-\tilde\alpha&(\varepsilon_{1s}-E)\delta-\gamma\\ (\varepsilon_{1s}-E)\delta-\gamma&\varepsilon_{1s}-E-\tilde\alpha\\ \end{vmatrix}=(\varepsilon_{1s}-E-\tilde\alpha)^2-((\varepsilon_{1s}-E)\delta-\gamma)^2=0 $$
$$ \begin{aligned} &\varepsilon_{1s}-E-\tilde\alpha=\mp\{(\varepsilon_{1s}-E)\delta-\gamma\}\\ &(1\pm\delta)(\varepsilon_{1s}-E)=\tilde\alpha\pm\gamma\\ &\varepsilon_{1s}-E=\frac{\tilde\alpha\pm\gamma}{1\pm\delta}\\ \end{aligned} $$
この時の解は、
$$ \begin{aligned} &\begin{pmatrix} \varepsilon_{1s}-E-\tilde\alpha&(\varepsilon_{1s}-E)\delta-\gamma\\ (\varepsilon_{1s}-E)\delta-\gamma&\varepsilon_{1s}-E-\tilde\alpha\\ \end{pmatrix}\begin{pmatrix}c_1\\c_2\end{pmatrix}=\\ &\frac{1}{1\pm\delta}\begin{pmatrix} \tilde\alpha\pm\gamma-(1\pm\delta)\tilde\alpha&(\tilde\alpha\pm\gamma)\delta-(1\pm\delta)\gamma\\ (\tilde\alpha\pm\gamma)\delta-(1\pm\delta)\gamma&\tilde\alpha\pm\gamma-(1\pm\delta)\tilde\alpha\\ \end{pmatrix}\begin{pmatrix}c_1\\c_2\end{pmatrix}=\\ &\frac{1}{1\pm\delta}\begin{pmatrix} \pm\gamma\mp\delta\tilde\alpha&\tilde\alpha\delta-\gamma\\ \tilde\alpha\delta-\gamma&\pm\gamma\mp\delta\tilde\alpha\\ \end{pmatrix}\begin{pmatrix}c_1\\c_2\end{pmatrix}=\\ &\frac{\gamma-\tilde\alpha\delta}{1\pm\delta}\begin{pmatrix} \pm 1&-1\\ {}-1&\pm 1 \end{pmatrix}\begin{pmatrix}c_1\\c_2\end{pmatrix}=0\\ \end{aligned} $$
すなわち、
$\begin{pmatrix}c_1\\c_2\end{pmatrix}\propto\begin{pmatrix}1\\\pm1\end{pmatrix}$ のとき、
$$E=\varepsilon_{1s}-\frac{\tilde\alpha\pm\gamma}{1\pm\delta}$$
となる。解の規格化は、
$$ \begin{aligned} \braket{\Phi}{\Phi}&=A^2\big[\braket{1}{1}\pm\braket{1}{2}\pm\braket{2}{1}+\braket{2}{2}\big]\\ &=A^2(2\pm 2\delta)=1 \end{aligned} $$
より、$A=\frac{1}{\sqrt{2(1\pm\delta)}}$ となるから、
$$\begin{pmatrix}c_1\\c_2\end{pmatrix}=\frac{1}{\sqrt{2(1\pm\delta)}}\begin{pmatrix}1\\\pm1\end{pmatrix}$$
である。
ヒュッケル近似によりエネルギーが少しだけ変化したが、解の形は変らず、 定性的には良い近似になっていることが分かる(?)。
このように少しまじめに考えたやり方は拡張ヒュッケル法と呼ばれる?
以下、特に断らない場合には普通のヒュッケル法(単純ヒュッケル)を使う。
電子が複数ある影響†
上で考えたのは陽子2つの周りを1つに電子がいる状況。
すなわち、水素分子 H2 ではなく水素分子イオン H2+ である。
水素分子では電子が2つになるため、電子・電子相互作用が入る。
通常、電子・電子相互作用は平均場近似で取り入れる。 すなわち他の電子により部分的に遮蔽された原子核からのポテンシャル中での 1電子の運動を考えることになる。
電子の空間分布が偏りを持つ場合、それぞれの原子核からのポテンシャルは等しくならないが、 ヒュッケル近似ではその影響は無視される。
最終的に1電子軌道から多電子軌道を構成する際には交換相互作用が現れる。
このようなことから、話はそれほど単純ではないとはいえ、 ヒュッケル近似から導かれる以下で見るような性質は、 実際の系でも強く表れる。
4つの原子からなる仮想的な四角い分子†
4つの同種原子が正方形に並んだ仮想的な分子を考える。
4個の原子軌道(AO : atomic orbital):$\ket 1,\ket 2,\ket 3,\ket 4$
分子軌道(MO : molecular orbital):$\ket\Phi=c_1\ket 1+c_2\ket 2+c_3\ket 3+c_4\ket 4$
ヒュッケル近似を用いて、
- 波動関数は重ならないとする $\braket{i}{j}=0\ \ (i\ne j)$
- クーロン積分 $\braketm{i}{\hat H}{i}=-\alpha$
- 隣接する原子核からだけ相互作用を受けるものとする $\braketm{i}{\hat H}{j}=0\ \ (i,j が離れているとき)$
- 飛び移り積分 $\braketm{i}{\hat H}{j}=-\gamma\ \ (i,j が隣り合うとき)$
とすると、1-2, 2-3, 3-4, 4-1 の間にのみ相互作用があるため、
$$ \begin{pmatrix} {}-\alpha & -\gamma & 0 & -\gamma\\ {}-\gamma & -\alpha & -\gamma & 0 \\ 0 & -\gamma & -\alpha & -\gamma \\ {}-\gamma & 0 & -\gamma & -\alpha \\ \end{pmatrix} \begin{pmatrix}c_1\\c_2\\c_3\\c_4\end{pmatrix} = E\begin{pmatrix}c_1\\c_2\\c_3\\c_4\end{pmatrix} $$
これを解くとエネルギーは
$$E=-a-2g,\ -a,\ -a,\ -a+2g$$
対応するベクトルは、
$$\psi=\frac{1}{\sqrt 4}\big(|1\rangle+|2\rangle+|3\rangle+|4\rangle\big)$$
$$\psi=\frac{1}{\sqrt 2}\big(-|2\rangle+|4\rangle\big)$$
$$\psi=\frac{1}{\sqrt 2}\big(-|1\rangle+|3\rangle\big)$$
$$\psi=\frac{1}{\sqrt 4}\big(-|1\rangle+|2\rangle-|3\rangle+|4\rangle\big)$$
つまり、
++ 0- -0 -+ ++ +0 0+ +-
の形になる。
一番左は4つのボンドすべてが結合性、
一番右は4つのボンドすべてが反結合性に対応する。
真ん中の2つは対角線なのでまったく相互作用のない形。
この2つは縮退しているため、その一時結合、例えば
-- +- ++ +-
なども固有値 $-\alpha$ の固有関数になる。
これら結合性の相互作用が2つと反結合性の相互作用が2つとで 打ち消し合って、ちょうど何の相互作用もない時と同じ値になっている。
結晶を作る†
一次元結晶 = $N$個の原子を直線状に並べる†
上の4つの時を拡張すれば、解くべき固有値問題は
$$ \begin{pmatrix} {}-\alpha&-\gamma&&&\\ {}-\gamma&-\alpha&-\gamma\\ &-\gamma&-\alpha&\ddots\\ &&\ddots&\ddots&-\gamma\\ &&&-\gamma&-\alpha \end{pmatrix} \begin{pmatrix} c_1\\c_2\\\vdots\\\vdots\\c_N \end{pmatrix} = E \begin{pmatrix} c_1\\c_2\\\vdots\\\vdots\\c_N \end{pmatrix} $$
あるいは同じ意味だが、
$$ \begin{pmatrix} 0&-1&&&\\ {}-1&0&-1\\ &-1&0&\ddots\\ &&\ddots&\ddots&-1\\ &&&-1&0 \end{pmatrix} \begin{pmatrix} c_1\\c_2\\\vdots\\\vdots\\c_N \end{pmatrix} = \frac{E+\alpha}{\gamma} \begin{pmatrix} c_1\\c_2\\\vdots\\\vdots\\c_N \end{pmatrix} $$
Mathematica を使えば解くのは簡単。
上式の通り $\alpha$ は固有値をずらすだけ、 $\gamma$ もスケールするだけなので、 便宜的に $\alpha=0,\gamma=1$ として解いて、固有値を小さいものから順にプロットすると、 ($N=50$ とした)
LANG:mathematica
a = Array[If[Abs[#1 - #2] == 1 , -1, 0] &, {50, 50}];
solution = Eigensystem[a];
ListPlot[Sort[solution[[1]] // N]]
ListPlot[Table[SortBy[Transpose[{solution[[1]] // N, solution[[2]]}], First][[n]] // Last,
{n, 1, 5}], PlotMarkers -> Automatic, PlotLegends -> Automatic]
何やら cos 的な関数が見えてくる。 (縦軸は $\gamma$ を単位としたエネルギー、横軸はエネルギーの低いほうから順に振った量子数)
エネルギーの低いほうから固有ベクトルを5つプロットすると、 固定端に対する弦の振動のような関数が見える。
エネルギーが高くなるに従い、波長が短くなり、波数が大きくなっていく。
ブロッホ波†
なぜ正弦波が現れたのか?
上記方程式を整理すると、
$$c_{n+1}+\frac{E+\alpha}{\gamma}c_n+c_{n-1}=0$$
となる。
ただし、$n=1\sim N$ で $c_0=c_{n+1}=0$ とした。
この方程式は固体物理学で1次元格子振動を扱う際に学んだ、 「互いにバネで繋がれたN個の質点」の方程式とそっくりな形をしている。
互いにバネで繋がれたN個の質点 を思い出す†
個体物理では1次元格子振動のモデルとして、 各質点の変位を $u_i$ として、
$$K(u_{n+1}-u_n)-K(u_n-u_{n-1})=M\ddot u_n$$
という形の方程式を解いた。ただし $K$ は質点を繋ぐバネのバネ定数、 $M$ は質点の質量。
ここでも固定端の条件は $u_0=u_{N+1}=0$ で与えられる。少々変形して、
$$u_{n+1}-2u_n+u_{n-1}=\frac{M}{K}\ddot u_n$$
を行列で表せば、
$$ \begin{pmatrix} {}-2&1\\ 1&-2&1\\ &1&\ddots&\ddots\\ &&\ddots&\ddots&1\\ &&&1&-2 \end{pmatrix} \begin{pmatrix} u_1\\u_2\\\vdots\\\vdots\\u_N \end{pmatrix} =\frac{M}{K}\frac{d^2}{dt^2} \begin{pmatrix} u_1\\u_2\\\vdots\\\vdots\\u_N \end{pmatrix} $$
したがって、
$$ \begin{pmatrix} {}-2&1\\ 1&-2&1\\ &1&\ddots&\ddots\\ &&\ddots&\ddots&1\\ &&&1&-2 \end{pmatrix} \begin{pmatrix} u_1\\u_2\\\vdots\\\vdots\\u_N \end{pmatrix} =-\omega^2\frac{M}{K} \begin{pmatrix} u_1\\u_2\\\vdots\\\vdots\\u_N \end{pmatrix} $$
となる固有値・固有ベクトルが求まれば、
$$ \frac{d^2}{dt^2} \begin{pmatrix} u_1\\u_2\\\vdots\\\vdots\\u_N \end{pmatrix}=-\omega^2 \begin{pmatrix} u_1\\u_2\\\vdots\\\vdots\\u_N \end{pmatrix} $$
より、
$$\bm u(t)=e^{\pm i\omega t}\bm u(0)$$
として方程式が解ける。
この固有値問題は $N$ 次元対称行列に対するものであるから、 重複度を含めて $N$ 個の実数固有値と、対応する一時独立な $N$ 個の固有ベクトルが存在する。
良く知られるように、質点間の距離を $\Delta x$ として、
$$u_n(t)=e^{ink\Delta x}$$
と置けば上記方程式は
$$\Big(e^{ik\Delta x}-2+e^{-ik\Delta x}\Big)e^{ink\Delta x}=-\omega^2\frac{M}{K}e^{ink\Delta x}$$
となり、両辺を $e^{ink\Delta x}$ で割って、
$$e^{ik\Delta x}-2+e^{-ik\Delta x}=-\omega^2\frac{M}{K}$$
$$\omega=\pm\sqrt{\frac{2K}{M}}\sqrt{1-\cos ik\Delta x}$$
を満たす $\omega,k$ が固有値、固有ベクトルの候補となる。
このとき分散関係($\omega(k)$ のグラフ)は $\sqrt{K/M}$ を単位として、
LANG:mathematica
Plot[Sqrt[2 (1 - Cos[Pi x])], {x, 0, 1}]
こんな形になる。
ただし、上でも述べた通り $k$ や $\omega$ の値は このグラフ上の任意の値をとれるわけではなく、$u_0=u_{N+1}=0$ の条件から許される値はとびとびになる。
$u_n(t)=e^{ink\Delta x}$ の形でこの「境界条件」を満たすことはできないが、 ある $\omega$ の値に足して $k$ が条件を満たすとき、同時に $-k$ も条件を満たすことに注意して($\because\cos(\theta)=\cos(-\theta)$)、
$$u_n(t)\propto e^{ink\Delta x}-e^{-ink\Delta x} \propto \sin nk\Delta x$$
と置き、$k_m=m\pi/\Delta x(N+1)$ とすれば、$m=1\dots N$ に対して $\bm u_m$ は線形独立になる。例えば $N=5$ の場合、$\{u_m\}_{m=1\dots N}$ は、
LANG:mathematica
Module[{nn}, nn = 5;
Plot[Table[Sin[n m Pi/(nn + 1)], {m, 1, nn}] // Evaluate, {n, 0, nn + 1},
Mesh -> 5, MeshStyle -> Directive[PointSize[Large]], ImageSize -> Large]
]
グラフにはサイン波を表示したが、実際には格子点上の値しか意味を持たないため、 例えば $m=(N+1)-1$ と $m=(N+1)+1$ とは符号を除いて同一の値を取り、 独立な解を与えない。
LANG:mathematica
Module[{nn}, nn = 5;
Plot[Table[
If[m > nn, -1, 1] Sin[n m Pi/(nn + 1)], {m, {nn, nn + 2}}] // Evaluate,
{n, 0, nn + 1}, Mesh -> 5, MeshStyle -> Directive[PointSize[Large]]]
]
これが $m=1\dots N$ の範囲に限られる理由となる。
これらに対応する $k_m$ のそれぞれに対して $\omega=\pm\sqrt{\frac{2K}{M}}\sqrt{1-\cos ik\Delta x}$ の2つの $\omega$ が対応するが、これらの線形結合で実数解を求めれば $\cos(\omega t+\delta)$ の形に限られることになる。
閑話休題(ブロッホ波再び)†
$n$ 番目の原子位置を $R_n=n\Delta R$ として、
$$c_n=e^{ikR_{n-1}}c_1$$
と置けば、このベクトルは
$$e^{ik\Delta R}+\frac{E+\alpha}{\gamma}+e^{-ik\Delta R}=0$$
より、
$$E=-\alpha-2\gamma\cos(k\Delta R)$$
の固有ベクトルとなっている。例えば $\alpha=\gamma=1$ とすると、 $E(k)$ は上式のとおり cos 的な、こんなグラフになる。
LANG:mathematica
Plot[-1 - Cos[Pi x], {x, 0, 1}]
上記の固体物理で学んだ分散関係とは一見異なって見えるが、それは $E\leftrightarrow \omega^2$ の関係にあるためであり、固体物理の分散関係で $\omega^2$ をプロットすれば同じ形の プロットが得られる。
固有ベクトルの形は上で見たように、$R_0$ サイトと $R_{N+1}$ サイトを固定端とする、正弦波的な形になる。
$$c_n^m\propto \sin(k_mR_n)$$
$$k_m=\frac{m\pi}{(N+1)\Delta R}$$
周期境界条件†
上記の例では固定端となっていたが、これを周期的境界条件にしてみると、 分散関係は固定端の場合と同じだが、周期境界条件で許される波数は
$$k_m=\frac{2m\pi}{(N+1)\Delta R}$$
であり、同じ波数に対して
$$c_n^{m,s}\propto \sin(k_mR_n)$$
と、
$$c_n^{m,c}\propto \cos(k_mR_n)$$
が縮退する。
したがって、固有値問題
$$ \begin{pmatrix} 0&-1&&&\red{-1}\\ {}-1&0&-1\\ &-1&0&\ddots\\ &&\ddots&\ddots&-1\\ \red{-1}&&&-1&0 \end{pmatrix} \begin{pmatrix} c_1\\c_2\\\vdots\\\vdots\\c_N \end{pmatrix} = \frac{E+\alpha}{\gamma} \begin{pmatrix} c_1\\c_2\\\vdots\\\vdots\\c_N \end{pmatrix} $$
に対する固有値を小さいものから並べれば、 (赤で示した $\red{-1}$ が周期性を担っている)
LANG:mathematica
solution = Array[ If[Abs[#1 - #2] == 1 || (#1 == 1 && #2 == 50) || (#1 == 50 && #2 == 1), -1, 0] &, {50, 50}] //
Eigensystem[#] &;
ListPlot[Sort[solution[[1]] // N]]
Transpose[{solution[[1]] // N, solution[[2]] // N}] //
SortBy[#, First] & // Map[Last, #] & // Orthogonalize //
ListPlot[#[[{1, 2, 3, 4, 5}]], PlotMarkers -> Automatic, PlotLegends -> Automatic] &
このように2つずつが等しいエネルギーを持つことになる。
ただし基底状態は定数関数なので sin, cos の区別が無く、縮退しない。
また上のように原子数が偶数の場合、エネルギー最大の状態は隣同士で符号が入れ替わる形になるため、 sin 的な解は存在せず、やはり縮退しない。
原子数が奇数の場合は、互い違いに入れ替わるベクトルは周期境界条件を満たさず解にならないため、 エネルギー最大の状態は縮退する。
固有ベクトルをエネルギーの低いものから5つ並べれば、
となる。
状態密度†
今の場合 $k_m$ は等間隔に並ぶため、状態密度は $\frac{\PD k}{\PD E}$ に比例する。 ここでは $1/\sin k\Delta R$ となって、
cos の上下端で状態密度が発散するのは1次元結晶の特徴である。
1次元状態密度†
$k$ 空間で状態が等間隔に存在しているとき、 つまり例えば $k=n\Delta k$ に状態があるとき、 $k$ 空間での状態密度(単位波数当たりの状態密度)は一定値 $1/\Delta k$ である。
分散関係 $E(k)$ が単調であれば、$E$ 空間での状態密度は
$$\rho(E)dE=\frac{dk}{\Delta k}$$
より、
$$\rho(E)=\frac{1}{\Delta k}\left.\frac{\PD k}{\PD E}\right|_E$$
である。
したがって、上のように $\frac{dE}{dk}=0$ となる点においては、 一次元状態密度は発散する。
一般には $E=E(k)$ となるような $k$ は複数あるので、
$$\rho(E)=\frac{1}{\Delta k}\sum_n\left.\frac{\PD k}{\PD E}\right|_{k=k_n} $$
としなければならない。
この式は、形式的には次のように書くこともできる。
$$\rho(E)=\frac{1}{\Delta k}\int \delta(E(k)-E)\,dk $$
$\frac{\PD k}{\PD E}$ の因子がなくなったのは、 それが暗に $\delta(E(k)-E)$ に含まれているためだ。
つまり、$E(k_0)=E_0$ であるとき、その周辺で
$$\delta(E(k_0)-E_0)=\delta(k-k_0)\left.\frac{\PD E}{\PD k}\right|_{k=k_0}$$
が成り立つ。すなわち、$k=k_1,k_2,k_3,\dots$ で $E(k)=k$ となるとき、
$$\rho(E)=\frac{1}{\Delta k}\int \delta(E(k)-E)\,dk=\frac{1}{\Delta k}\sum_n\left.\frac{\PD k}{\PD E}\right|_{k=k_n} $$
となる。$E$ で書かれたデルタ関数を $k$ で積分すると $\frac{\PD E}{\PD k}$ を集めて回ることができるのである。
運動量†
$$ \begin{aligned} \Phi_k(x) &=\sum_{n=1}^N e^{ikn\Delta x}\phi(x-n\Delta x)\\ &=e^{ikx}\underbrace{\sum_{n=1}^N e^{-ik(x-n\Delta x)}\phi(x-n\Delta x)}_{u_k(x)}\\ \end{aligned} $$
で表されるブロッホ状態に対して、速度の期待値を求めてみる。*1http://www1.doshisha.ac.jp/~ma... を参考にした
まず、
$$ \begin{aligned} \hat p\Phi_k &= \frac{\hbar}{i}\frac{\PD}{\PD x}e^{ikx}u_k(x)\\ &= \hbar ke^{ikx}u_k(x)+e^{ikx}\frac{\hbar}{i}\frac{\PD}{\PD x}u_k(x)\\ &= \hbar ke^{ikx}u_k(x)+e^{ikx}\hat p u_k(x)\\ &= e^{ikx}(\hbar k+\hat p) u_k(x)\\ \end{aligned} $$
$$ \begin{aligned} \hat p^2\Phi_k &= \hat p\,e^{ikx}(\hbar k+\hat p) u_k(x)\\ &= \hbar k e^{ikx}(\hbar k+\hat p) u_k(x)+e^{ikx}(\hbar k+\hat p) \hat p\,u_k(x)\\ &= e^{ikx}(\hbar k+\hat p)^2 u_k(x)\\ \end{aligned} $$
を用いてシュレーディンガー方程式を書き直すと、
$$ \left(\frac{\hat p^2}{2m}+V\right)\Phi_k=\varepsilon(k)\Phi_k $$
$$ e^{ikx}\left\{\frac{(\hbar k+\hat p)^2}{2m}+V\right\}u_k=e^{ikx}\varepsilon(k)u_k $$
すなわち、$u_k$ に対するシュレーディンガー方程式が次のように得られる。
$$ \underbrace{\left\{\frac{(\hbar k+\hat p)^2}{2m}+V\right\}}_{\hat H(k)}u_k=\varepsilon(k)u_k $$
ここに現れるハミルトニアンは $k$ に依存するが、 このような場合 ファインマンの定理 により、
$$ \int u_k^*\frac{\PD \hat H}{\PD k}u_k\,dx=\frac{\PD \varepsilon}{\PD k} $$
が成り立つ。ここでは $\PD \hat H/\PD k=\hbar (\hat p+\hbar k)/m$ であり、
$$ \int u_k^*\frac{\hbar}{m}(\hat p+\hbar k)u_k\,dx=\frac{\PD \varepsilon}{\PD k} $$
を得る。一方で、
$$ \begin{aligned} \langle v\rangle &=\int\Phi_k^*\frac{\hat p}{m}\Phi_k\,dx\\ &=\int \cancel{e^{-ikx}}u_k^*\ \cancel{e^{ikx}}\frac{(\hat p+\hbar k)}{m}u_k\,dx\\ &=\int u_k^*\frac{(\hat p+\hbar k)}{m}u_k\,dx\\ \end{aligned} $$
より、
$$ \langle v\rangle=\frac{1}{\hbar}\frac{\PD \varepsilon}{\PD k} $$
を得る。
これと正準方程式 $\dot x=\frac{\PD H}{\PD p}$ とを比べると、 $\hbar k$ が $x$ に対応する正準運動量になっていそうな気がしてくる。
ただ、ここまで良く見返してみると、上の議論では $V$ や $u_k$ の周期性など物理的な条件を一切使っていない。
それでは、任意のハミルトニアンの任意の固有関数に対して、 任意に決めた $k$ を使って同様の議論ができてしまうのではないか?
おかしな波数をとってみる†
以下、ちょっと納得のいかない結果になってしまうため、慎重に。
あるポテンシャル $V$ に対する時間を含まないシュレーディンガー方程式の エネルギー固有値及び固有関数が、 ほとんど連続な量子数 $k$ を用いて $\varepsilon(k), \Phi_k(x)$ と書けるとする。
ポテンシャルの周期性や、波動関数がブロッホ状態であることなどは仮定していないことに注意せよ。
$k$ を別の量子数 $k'$ を使って $k=k(k')$ と表したうえで、
$$ \Phi_k(x) =e^{ik'x}\underbrace{e^{-ik'x}\Phi_k(x)}_{u_{k'}(x)} $$
のように無理やり $e^{ik'x}$ をくくりだした形から始めて、速度の期待値を求める。
この関数に $\hat p$ を作用させると、上記と同様にして $\hbar k'+\hat p$ が間に挟まる形を導ける。
$$ \begin{aligned} \hat p\Phi_k &= \frac{\hbar}{i}\frac{\PD}{\PD x}e^{ik'x}u_{k'}(x)\\ &= \hbar k'e^{ik'x}u_{k'}(x)+e^{ik'x}\frac{\hbar}{i}\frac{\PD}{\PD x}u_{k'}(x)\\ &= e^{ik'x}(\hbar k'+\hat p) u_{k'}(x)\\ \end{aligned} $$
$$ \begin{aligned} \hat p^2\Phi_k &= \hat p\,e^{ik'x}(\hbar k'+\hat p) u_{k'}(x)\\ &= \hbar k' e^{ik'x}(\hbar k'+\hat p) u_{k'}(x)+e^{ik'x}(\hbar k'+\hat p) \hat p\,u_{k'}(x)\\ &= e^{ik'x}(\hbar k'+\hat p)^2 u_{k'}(x)\\ \end{aligned} $$
結局これは、
$$ \begin{aligned} \hat p\,f(x)&=\hat p\,e^{ikx}e^{-ikx}f(x)\\ &=e^{ikx}(\hbar k +\hat p)e^{-ikx}f(x)\\ &=e^{ikx}e^{-ikx}(\hbar k-\hbar k+\hat p)f(x)\\ &=\hat p\,f(x)\\ \end{aligned} $$
という恒等式を表しているに過ぎない。
上記を用いてシュレーディンガー方程式を書き直す。
$$ \left(\frac{\hat p^2}{2m}+V\right)\Phi_k=\varepsilon(k(k'))\Phi_k $$
$$ e^{ik'x}\left\{\frac{(\hbar {k'}+\hat p)^2}{2m}+V\right\}u_{k'}=e^{ik'x}\varepsilon(k(k'))u_{k'} $$
すなわち、$u_{k'}$ に対するシュレーディンガー方程式が次のように得られる。
$$ \underbrace{\left\{\frac{(\hbar k'+\hat p)^2}{2m}+V\right\}}_{\hat H(k')}u_{k'}=\varepsilon(k(k'))u_{k'} $$
ここに現れるハミルトニアンは $k'$ に依存するので、 「ファインマンの定理が成り立つならば」
$$ \int u_{k'}^*\frac{\PD \hat H}{\PD k'}u_{k'}\,dx=\frac{\PD \varepsilon}{\PD k'} $$
となる。
で、あとは一直線。$\PD \hat H/\PD k'=\hbar (\hat p+\hbar k')/m$ より、
$$ \int u_{k'}^*\frac{\hbar}{m}(\hat p+\hbar k')u_{k'}\,dx=\frac{\PD \varepsilon}{\PD k'} $$
一方で、
$$ \begin{aligned} \langle v\rangle &=\int\Phi_k^*\frac{\hat p}{m}\Phi_k\,dx\\ &=\int \cancel{e^{-ik'x}}u_{k'}^*\ \cancel{e^{ik'x}}\frac{(\hat p+\hbar k')}{m}u_{k'}\,dx\\ &=\int u_{k'}^*\frac{(\hat p+\hbar k')}{m}u_{k'}\,dx\\ \end{aligned} $$
より、
$$ \begin{aligned} \langle v\rangle &=\frac{1}{\hbar}\frac{\PD \varepsilon}{\PD {k'}}\\ &=\frac{1}{\hbar}\frac{\PD \varepsilon}{\PD k}\frac{\PD k}{\PD k'} \end{aligned} $$
となって、右辺は $k'$ の取り方によって値が変わってしまう。
どうしてこうなった?
怪しいのはファインマンの定理のところだけのように思われる。
英語版の Wikipedia にも書かれているように、 ファインマンの定理が成立するためには関数空間やハミルトニアンに対して一定の条件が必要になる。 Carfì, David (2010). "The pointwise Hellmann–Feynman theorem". AAPP: Physical, Mathematical, and Natural Sciences. 88 (1). no. C1A1001004. doi:10.1478/C1A1001004
たぶん、正しい $k$ を取ったときのみ上記の演算が許される?
ファインマンの定理再考†
正しく $k$ を取った場合、
$$ \Phi_k(x) =e^{ikx}\underbrace{\sum_{n=1}^N e^{-ik(x-n\Delta x)}\phi(x-n\Delta x)}_{u_k(x)} $$
この $u_k$ は結晶の端を除いて周期 $\Delta x$ の周期関数になっている。
$u_k$ を $k$ で微分すると
$$ \frac{\PD}{\PD k}u_k(x) =-ie^{ikx}\sum_{n=1}^N (x-n\Delta x)e^{-ik(x-n\Delta x)}\phi(x-n\Delta x) $$
となって、これも周期 $\Delta x$ の周期関数。
おそらくこの、「周期関数になっている」というのが重要な条件になっているのだと思われる。
で気づいたのが、そもそも周期的境界条件以外の束縛状態の定常状態を考える限り、 運動量あるいは速度の期待値が非ゼロになるような関数は解空間に含まれていないことだ。
箱型ポテンシャルや調和振動子では波数 $k$ の成分は必ず 波数 $-k$ の成分とある決まった係数で線形結合を取り、 全体での運動量の期待値をゼロにしないと境界条件を満たさない。
定常的に非ゼロの運動量を持った解は束縛されていないのだからこれは当然。
ファインマンの定理では $u_k$ や $\PD u_k/\PD k$ を含む 関数ベクトル空間でハミルトニアンがエルミートであることを仮定しているが、 適当な $k'$ を取ってしまうとその空間でハミルトニアンがエルミートでは なくなってしまうのが問題。*2演算子のエルミート性については 量子力学Ⅰ/固有値と期待値#qf83b503(./?%E9%87%8F%E5%AD%90%E5%8A%9B...) を参照のこと
周期的境界条件では領域の端でちょうど関数値が等しくなることから 内積を部分積分した際に現れる積分値がゼロになり、 運動量演算子のエルミート性が保たれる。
ただ実は、$\Phi_k$ に対して $u_k$ を周期関数にするには 必ずしも $k'=k$ としなければならないわけではなくて、 $k'=k+G$ となっていても良い。ただしこの $G$ は結晶格子の逆格子ベクトル。
このとき $\PD k'/\PD k=1$ なので、$k$ を使っても、 $k'$ を使っても、速度の期待値は変わらない。
これが結晶の分散関係がブリルアンゾーンをまたいで周期的に繰り返す理由になっている。
今の場合†
$$E=-\alpha-2\gamma\cos(k\Delta x)$$
$$\frac{\PD E}{\PD k}=2\Delta x\gamma\sin(k\Delta x)$$
より、
$$ \langle v\rangle_k=\frac{2\gamma\Delta x}{\hbar}\sin(k\Delta x) $$
確かに、$k\to k+G$ としても $\langle v\rangle$ の値は変わらない形になっている。
LANG:Mathematica
Plot[Sin[Pi x], {x, -1, 1}]
$k\sim 0$ では $\langle v\rangle\propto k$ だが、 ある程度 $k$ が大きくなると速度は徐々に上がらなくなり、 $k\Delta x=\pi/2$ で最大値 $2\gamma\Delta x/\hbar$ を取り、 それ以上では $k$ が増えると $\langle v\rangle$ は減少し、 $k\Delta x=\pi$ で再び静止する。
有効質量†
外力 $f$ が短時間 $\Delta t$ 加わって、 速度の期待値が $\Delta v$ 増えたとする。 このとき粒子は $\langle v\rangle \Delta t$ 進んでいるので、 外力から得たエネルギーは $\Delta E=\langle v\rangle \Delta t f$ である。
この過程で波数が $\Delta k$ 増えたとすると、
$$ \Delta E=\frac{\PD E}{\PD k}\Delta k=\langle v\rangle \Delta t f $$
ここに上で得た $\langle v\rangle$ の表式を代入すれば、
$$ \frac{\PD E}{\PD k}\Delta k=\frac{1}{\hbar}\frac{\PD E}{\PD k} \Delta t f $$
より、
$$ \frac{dk}{dt}=f/\hbar $$
を得る。
すなわち、一定の外力の下では $k$ は時間とともに線形に増加する。
一方、このとき粒子の加速度は、
$$ \frac{d}{dt}\langle v\rangle=\frac{d\langle v\rangle}{dk}\frac{dk}{dt}=\frac{1}{\hbar^2}\frac{\PD E}{\PD k^2}f $$
より、ニュートン方程式 $f=m\frac{d}{dt}\langle v\rangle$ と比較すると、 $m^*$ を有効質量として
$$\frac{1}{m^*}=\frac{1}{\hbar^2}\frac{\PD E}{\PD k^2}$$
の関係が得られる。
エネルギー対波数の分散関係を基準とすれば、
その傾きが速度であり、
波数の時間変化が力そのものであるため、
分散関係の二次微分が質量の逆数に対応する。
二次微分が大きければ同じ力に対する速度の増加率が大きい = 質量は小さい
二次微分が小さければ同じ力に対する速度の増加率が小さい = 質量は大きい
古典論との対応を見ておこう。
ハミルトニアンが運動エネルギーと保存力によるポテンシャルのみを含んでいる場合、 古典論において正準方程式から
$$\dot p=-\frac{\PD H}{\PD x}=-\frac{\PD V}{\PD x}=f$$
$$\dot x=\frac{\PD H}{\PD p}$$
$$ \begin{aligned} \ddot x&=\frac{d}{dt}\frac{\PD H}{\PD p}\\ &=\frac{\PD}{\PD p}\frac{dH}{dt}\\ &=\frac{\PD}{\PD p}\frac{\PD H}{\PD p}\dot p\\ &=\frac{\PD^2 H}{\PD p^2}f\\ \end{aligned} $$
のようにして、
$$\frac{1}{m}=\frac{\PD^2 H}{\PD p^2}$$
の関係を導けることに対応している。
3次元空間での一般形は、
$$\hbar\dot{\bm k}=-\bm\nabla_x H=-\bm\nabla_x V=\bm f$$
$$\dot{\bm x}=\frac{1}{\hbar}\bm \nabla_k H$$
$$ \begin{aligned} \ddot{\bm x}&=\hbar\frac{d}{dt}\bm\nabla_k H\\ &=\frac{1}{\hbar}\bm\nabla_k \frac{dH}{dt}\\ &=\frac{1}{\hbar^2}\bm\nabla_k (\bm\nabla_k H\cdot \hbar\dot{\bm k})\\ &=\frac{1}{\hbar^2}\Bigg(\frac{\PD^2 H}{\PD k_i\PD k_j}\Bigg) \hbar\dot{\bm k}\\\end{aligned} $$
のように、逆有効質量はテンソルになる。
今の場合†
$$m^*=\frac{\hbar^2}{2\Delta R^2\gamma\cos(k\Delta R)}$$
LANG:mathematica
Plot[1/Cos[Pi k], {k, 0, 1}]
$k\sim 0$ では $\cos(k\Delta R)\sim 1$ より $m^*=\frac{\hbar^2}{2\Delta R^2\gamma}$ となる。
一方、$k\sim \pi/\Delta R$ では $\cos(k\Delta R)\sim -1$ より $m^*=-\frac{\hbar^2}{2\Delta R^2\gamma}$ のように負の質量が現れる。
負の有効質量†
負の有効質量をもつ電子は、電場と同じ方向へ加速される。というか、もともと電場と逆方向に走っているので電場と逆方向の速度が減速される、というの方が分かりやすいか。通常の電子は電場と逆の方向へ加速されることに注意。
ここからどのような結論が導かれるだろうか?
電子が一つのとき†
バンドの下端に電子が1つある状況から、外場 $f$ によりこの電子を加速する。
散乱がなければ電子の波数は時間とともに一様に増加して、
$\frac{dk}{dt}=\frac{f}{\hbar}$ より、$k=\frac{f}{\hbar}t$
速度および位置は、
$$\langle v\rangle=\frac{2\gamma\Delta x}{\hbar}\sin(\Delta xft/\hbar)$$
$$\langle x\rangle=\int\langle v\rangle dt=\frac{2\gamma}{f}\cos(\Delta xft/\hbar)$$
のように振動する。
力が強くなれば速度変化が速くなり、振幅が小さくなる。
この振動はブロッホ振動と呼ばれる。
外場がゼロになると $\frac{dk}{dt}=0$ なので、等速直線運動を続けることになる。
実際には散乱があるので徐々に減衰して際安定状態に落ち込み、静止する。
散乱が強ければ電子が最高速度を超えることはなく、 平均的な速度が外場に比例するオーミックな電流が流れる。
電子が底の方に詰まっているとき†
最安定状態では $k$ 側と $-k$ 側に同じだけ電子がいるため、 電流は相殺されてゼロになる。
外場 $f$ がかかると、 すべての電子の $k$ が $\frac{dk}{dt}=\frac{f}{\hbar}$ で変化して、 $-k$ 側の電子が減り、$k$ 側の電子が増える。
その差の分だけ電流が流れる。
電子が半分以上詰まっているとき†
外場 $f$ がかかると、 すべての電子の $k$ が $\frac{dk}{dt}=\frac{f}{\hbar}$ で変化して、 $-k$ 側の電子が減り、$k$ 側の電子が増える。
$k\Delta x>\pi/2$ の電子は負の有効質量のために正方向の速度が減速され、
$k\Delta x<-\pi/2$ の電子は負の有効質量のために負方向の速度が加速されるが、
全体として見るとやはり負方向へ動く電子が減って、正方向へ動く電子が増えるため、
電流は力の加わった方向へ流れることになる。
詰まり具合と電流応答†
電子が底の方に少しだけ詰まっている時、 外場によって $k$ が少しだけ変わっても、 正側、負側とも速度が遅いので、電流の応答は小さい、と思われる。
電子が半分まで詰まっている時、 外場によって $k$ が少し変わるだけでも、 最高速で負側に動く電子が減って、最高速で正側に動く電子が増えるので、 電流の応答は大きい、と思われる。
電子がかなり上まで詰まっている時、 やはり正側、負側とも速度が遅いので、電流の応答は小さい、と思われる。
1個だけ残して残りが埋まっているとき†
外場 $f$ がかかると、 すべての電子の $k$ が $\frac{dk}{dt}=\frac{f}{\hbar}$ で変化するため、 空いた電子状態の $k$ も同じように変化する。
この電子状態は負の有効質量をもっているため、電子に加わる力とは反対方向に加速される。
電子の空状態なので、相対的に正の電荷を帯びている。
この電子の空準位がホールと呼ばれる。
2次元三角格子†
1原子状態をつなげてブロッホ波的な三角格子を作ると、これが実際の三角格子の解になっていることを確かめる。
$N$ 個の原子からなる三角格子中の原子位置を $\bm R_A$ で表し、 これらの原子を中心とする1原子状態を元にブロッホ状態を作る。
$$|\phi_A\rangle=\frac{1}{\sqrt{N}}\sum_{\bm R_A}e^{i\bm k\cdot\bm R_A}|\bm R_A\rangle$$
3角格子では最隣接原子が6個あり、基本ベクトルを $\bm a,\bm b$ と置けば
$$\bm a, -\bm a, \bm b, -\bm b,-\bm a+\bm b, \bm a-\bm b$$
に位置する。したがって係数間の方程式は
$$-\alpha C(\bm R_i)-\gamma\Big[C(\bm R_i+\bm a)+C(\bm R_i-\bm a)+C(\bm R_i+\bm b)+C(\bm R_i-\bm b)+C(\bm R_i-\bm a+\bm b)+C(\bm R_i+\bm a-\bm b)\Big]=EC(\bm R_i)$$
であり、$C(\bm R)=C(\bm 0)e^{i\bm k\cdot\bm R}$ と置いてみるとこれは、
$$ \begin{aligned} &-\alpha-\gamma\Big[e^{i\bm k\cdot\bm a}+e^{-i\bm k\cdot\bm a}+e^{i\bm k\cdot\bm b}+e^{-i\bm k\cdot\bm b}+e^{i\bm k\cdot(-\bm a+\bm b)}+e^{-i\bm k\cdot(-\bm a+\bm b)}\Big]=\\ &-\alpha-2\gamma\Big[\cos \bm k\cdot\bm a+\cos \bm k\cdot\bm b+\cos \bm k\cdot(\bm a-\bm b)\Big]=E\\ \end{aligned} $$
を満たす固有値 $E$ の固有ベクトルとなることが分かる。
今の場合 $\bm a=\begin{pmatrix}a\\0\end{pmatrix}$、 $\bm b=\begin{pmatrix}a/2\\\sqrt{3}\,a/2\end{pmatrix}$、 $$\bm a-\bm b=\begin{pmatrix}-a/2\\\sqrt{3}\,a/2\end{pmatrix}$$ であるから、その分散関係は次のようになる。
honeycomb[k_] =
Cos[k.{1, 0}] + Cos[k.{1/2, Sqrt[3]/2}] + Cos[k.{-1/2, Sqrt[3]/2}]
これらは、$\bm k=(k_x,k_y)$ に対して、対応する $E(\bm k)$ をプロットしたものである。
逆格子†
実空間での基本ベクトルが
$$\bm a=(a,0)$$
$$\bm b=(a/2,\sqrt 3a/2)$$
であるのに対応して、逆格子空間における基本ベクトルは、
$$\bm a^*=\frac{2\pi}{a}(1,-1/\sqrt 3)$$
$$\bm b^*=\frac{2\pi}{a}(0,2/\sqrt 3)$$
となる。
$$\bm a\cdot \bm a^*=\bm b\cdot \bm b^*=2\pi$$
$$\bm a\cdot \bm b^*=\bm b\cdot \bm a^*=0$$
に注意せよ。
- 6回対称性のあるΓ点は1種
- 3回対称性のあるK点は2種(K点、K'点)
- 2回対称性のあるM点は3種($M_1$点,$M_2$点,$M_3$点)
有効質量†
2次元なので、方向によって有効質量が異なる場合がある。
$$\frac{d\bm k}{dt}=\frac{1}{\hbar}\bm f$$
$$\langle \bm v\rangle=\frac{1}{\hbar}\bm \nabla_k H$$
$$\frac{d\langle \bm v\rangle}{dt}=\frac{1}{\hbar^2}\bm \nabla_k(\bm \nabla_k H\cdot \bm f)$$
より、
$$\frac{1}{m^*}=\frac{1}{\hbar^2}\Bigg(\frac{\PD^2 H}{\PD k_i\PD k_j}\Bigg)$$
三角格子の場合†
上で計算した分散関係を再掲すると、
ガンマ点、K'点、M点で速度ゼロ。その他の点では傾きに応じた方向の速度を持つ。
ガンマ点でエネルギー最大、曲率および有効質量は等方的で負の値を持つ。
K' 点でエネルギー最小、曲率および有効質量は等方的で正の値を持つ。
M点は鞍点で、曲率および有効質量は一方向に正、一方向に負の値を持つ。
原子の電子状態の等方性†
この手の議論では S 状態を出発点に仮定している場合が多い。
にもかかわらず、例えばグラフェンを扱う際にはπ電子を考えていたりする。
このような仮定は電子状態の等方性が問題にならないようにするためである。
電子状態が強い異方性を持っていると、$\alpha,\gamma$ の値が向きによって異なってしまう。
π電子は3次元空間で見ると非等方的だが、グラフェンシート内では等方的であるため、 その非等方性は問題にならない。
グラフェンの場合†
三角格子の単位胞に2つの原子 A, B がある構造。図ではそれぞれ白と赤。
系全体の波動関数を、A に対する三角格子波動関数と、B に対する三角格子波動巻子との線形結合で
$$\ket \Phi=C_A\ket{\Phi_A}+C_B\ket{\Phi_B}$$
と置き、$\braket{\Phi_A}{\Phi_B}=0$ を仮定すると、
$\braketm{\Phi_A}{\hat H}{\Phi}=E\braket{\Phi_A}{\Phi}$ より、
$$ C_A\underbrace{\braketm{\Phi_A}{\hat H}{\Phi_A}}_{h_{AA}}+ C_B\underbrace{\braketm{\Phi_A}{\hat H}{\Phi_B}}_{h_{AB}}=EC_A $$
などとなり、
$$ \begin{pmatrix} h_{AA}&h_{AB}\\ h_{BA}&h_{BB}\\ \end{pmatrix} \begin{pmatrix}C_A\\C_B\end{pmatrix} =E\begin{pmatrix}C_A\\C_B\end{pmatrix} $$
を得る。
$h_{AA},h_{BB}$ は等しく、三角格子のエネルギーと隣接原子からのクーロン相互作用とを加えたものになる。前者は上で解いたように波数に依存して変化するが、後者はブロッホ波の位相によらず、状態密度のみに依存する量であるため定数である。
$$h_{AA}=E_\mathrm{tri}(\bm k)-\tilde\alpha$$
$h_{AB}=h_{BA}^*$ であり、 隣り合う原子上の1原子波動関数の間に片方の原子核からのポテンシャルを挟んだものを 原子数分足したものになる。
$$ \begin{aligned} h_{AB}&=\braketm{\Phi_A}{H}{\Phi_B}\\ &\frac{1}{N}\sim \sum_{R_A}\sum_{R_{B}} \exp\big[-i\bm k\cdot(\bm R_A-\bm R_B)\big] \underbrace{\braketm{\bm R_A}{H}{\bm R_B}}_{-\gamma}\\ &= -\frac{1}{N}\gamma\sum_{R_A}\sum_{R_{B(隣接)}} \exp\big[i\bm k\cdot(\bm R_B-\bm R_A)\big]\\ &= -\frac{1}{N}\gamma\sum_{R_A} \Big( \exp\big[i\bm k\cdot\Delta\bm R_{BA,1}\big]+ \exp\big[i\bm k\cdot\Delta\bm R_{BA,2}\big]+ \exp\big[i\bm k\cdot\Delta\bm R_{BA,3}\big] \Big)\\ &= -\gamma \Big( \exp\big[i\bm k\cdot\Delta\bm R_{BA,1}\big]+ \exp\big[i\bm k\cdot\Delta\bm R_{BA,2}\big]+ \exp\big[i\bm k\cdot\Delta\bm R_{BA,3}\big] \Big)\equiv -\gamma f_k^*\\ \end{aligned} $$
2行目が $\sim$ で始まっているのは、 境界上の原子では周囲に3原子存在しない場合があり、 そのあたりの境界条件がうやむやになっているため。
上図の白丸を A サイトとすると、隣接 B サイトは
$$\Delta\bm R_{BA,1}=a(0,1/\sqrt 3)$$
$$\Delta\bm R_{BA,2}=a(-1/2,-1/2\sqrt 3)$$
$$\Delta\bm R_{BA,2}=a(1/2,-1/2\sqrt 3)$$
となるから、これらを代入すれば $\bm k$ の関数として $f_{\bm k}^*$ が求まる。
このとき、
$$ \begin{pmatrix} E_\mathrm{tri}(k)-\tilde\alpha&-\gamma f_{\bm k}^*\\ {}-\gamma f_{\bm k}&E_\mathrm{tri}(k)-\tilde\alpha\\ \end{pmatrix} \begin{pmatrix}C_A\\C_B\end{pmatrix} =E\begin{pmatrix}C_A\\C_B\end{pmatrix} $$
$$ \begin{pmatrix} 0&-\gamma f_{\bm k}^*\\ {}-\gamma f_{\bm k}&0\\ \end{pmatrix} \begin{pmatrix}C_A\\C_B\end{pmatrix} =\big(E-E_\mathrm{tri}(k)+\tilde\alpha\big)\begin{pmatrix}C_A\\C_B\end{pmatrix} $$
より、
$$E=\pm\gamma |f_k|+E_\mathrm{tri}(k)-\tilde\alpha$$
$$-\gamma f_k C_A=E C_B=\big(\pm\gamma N|f_k|+E_\mathrm{tri}(k)-\tilde\alpha\big)C_B$$
より、$f_k=|f_k|e^{i\phi_k}$ と置けば、
$$ \begin{pmatrix}C_A\\C_B\end{pmatrix}\propto \begin{pmatrix} \pm 1+(E_\mathrm{tri}(k)-\tilde\alpha)/\gamma |f_k|\\ {}-e^{i\phi_k} \end{pmatrix} $$
分散関係†
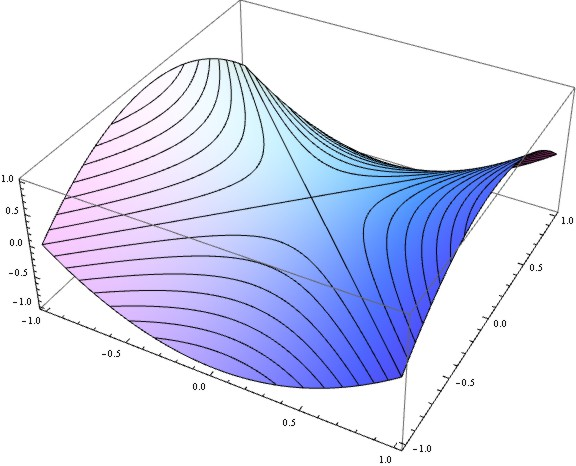
グラフェンの特異的な分散関係を見るために、まずは $E=\pm\gamma|f_k|$ のグラフを見る。
LANG: mathematica
Fk[k_] =
Exp[I k.{0, 1/Sqrt[3]}] +
Exp[I k.{-1/2, -1/(2 Sqrt[3])}] +
Exp[I k.{1/2, -1/(2 Sqrt[3])}]
Plot3D[{Abs[Fk[{x, y}]], -Abs[Fk[{x , y}]]},
{x, -10, 10}, {y, -10, 10}, PlotPoints -> 200]
分散関係はゼロを境に上下に対象であり、「卵のパック」のような形になる。
大きく膨らんでいる場所がガンマ点、 鋭くへこんでいる場所がK点、 鞍点となっているのがM点である。
中でもK点では、
$$f_k=\sum_{l=1}^3 e^{i\bm k\cdot \Delta R_l}$$
に対して $\bm k=\frac{2\pi}{a}(2/3,0)$ より、
$$ \begin{aligned} f_{\bm k}&=\exp(0)+\exp(i2\pi/3)+\exp(-i2\pi/3)\\ &=1+w+w^{-1}\\ &=0 \end{aligned} $$
ただし、$w=e^{i2\pi/3}$ は 1 の3乗根。
となって、$E_+(\bm k)=E_-(\bm k)=0$ すなわちギャップは閉じている。
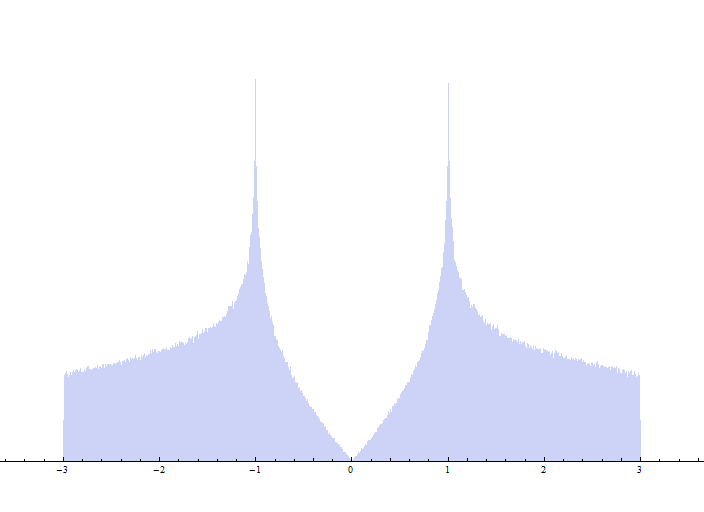
状態密度†
このとき、状態密度をモンテカルロ法により求めると、
LANG: mathematica
points = Table[{
Abs[Fk[{RandomReal[{-100, 100}], RandomReal[{-100, 100}]}]],
-Abs[Fk[{RandomReal[{-100, 100}], RandomReal[{-100, 100}]}]]},
{i, 1, 1000000}] // Flatten;
Histogram[points, {-4, 4, 0.05}]
ここでは $\gamma=1$ に取っている。
$E=\pm 3\gamma$ では状態密度はステップ関数的に立ち上がる。
これはΓ点のパラボリックな分散関係を反映している。
$E=\pm \gamma$ では発散する。
これはM点に存在する鞍点を反映している。
$E=0$ では線形に立ち上がる。
これはK点、K’点に存在する円錐状の分散関係を反映している。
以下、少し詳しく見てみる。
2次元状態密度†
1次元の時と同様に、2次元状態密度は形式的に
$$\rho(E)=\frac{1}{\Delta k_x\Delta k_y}\iint \delta(E(\bm k)-E)\,d\bm k $$
と書ける。この形は解析的に考えることができる場合には有用であるが、 数値計算可能な形ではないので、計算できる形に変形したい。
$$\rho(E)dE=\frac{dk_x}{\Delta k_x}\frac{dk_y}{\Delta k_y}$$
と書ければ良いのだが、 右辺の範囲が必ずしも $E\sim E+dE$ と一致しないため難しい。
$x,y$ 方向ではなく、$\bm e_1=\frac{\bm\nabla_k E}{|\bm\nabla_k E|}$ 方向と、それに垂直な $\bm e_2$ 方向に軸を取れば、
$$\delta\rho(E)dE=\oint\frac{dk_2}{\Delta k_2}\,\frac{dk_1}{\Delta k_1}$$
ただし $dE=|\nabla_k E|dk_1$。したがって、
$$\rho(E)=\frac{1}{\Delta k_1\Delta k_2}\oint |\nabla_k E|^{-1}dk_2$$
ここで、$\oint dk_2$ は $E(\bm k)=E$ となる等高線に沿って計算する。
とすると、格段にイメージはしやすくなるが、 これも数値計算可能な形は限られている。。。
ある点 $\bm k_0$ を中心に回転対称性があるとき†
$\delta \bm k\equiv \bm k-\bm k_0$ を用いて、 $E(\bm k)=E(|\bm k-\bm k_0|)=E(\delta k)$ と書けるから、
$\bm\nabla_{\bm k} E$ は円周方向を向くノルム一定のベクトルで、 $\int dk_2$ は円周に沿った長さ $2\pi r$ ($r$ は半径) に渡る積分になり、
$$ \begin{aligned} \rho(E)&=\frac{1}{\Delta k_x\Delta k_y}\int 2\pi\delta k\,\delta(E(\delta k)-E)\,d\delta k\\ &=\frac{1}{\Delta k_x\Delta k_y}2\pi\delta k\left.\frac{\PD \delta k}{\PD E}\right|_E\\ \end{aligned} $$
となる。
(1) ガンマ点の周りの円錐型の部分では
$$\frac{\PD \delta k}{\PD E}=\mathit{const.}$$
であるから、
$$\rho(E)\propto\frac{1}{\Delta k_x\Delta k_y}2\pi\delta k$$
のように $\delta k$ に対して1次で立ち上がる。
さらに
$$\frac{\PD \delta k}{\PD E}=\mathit{const.}$$
であるから、
$$\rho(E)\propto E$$
となる。
(2)ガンマ点の周りの回転放物面的な部分では [#x6fa440b]
$$E\propto \delta k^2$$
より、
$$\frac{\PD \delta k}{\PD E}\propto \frac{1}{\delta k}$$
であるから、
$$\rho(E)\propto\frac{2\pi}{\Delta k_x\Delta k_y}$$
のように定数値になる。
鞍点では†
$E-E_0=x^2-y^2$ の形の理想的な鞍点において、 特定のエネルギーでの切断面は
- $E=E_0$ では2つの直線が交わる形
- $E\ne E_0$ では双曲線
LANG:mathematica
Plot3D[x^2 - y^2, {x, -1, 1}, {y, -1, 1}, MeshFunctions -> {#3 &},
ImageSize -> Large, PlotPoints -> 101]
$\bm \nabla E=\begin{pmatrix}\PD E/\PD x\\\PD E/\PD y\end{pmatrix}=\begin{pmatrix}2x\\-2y\end{pmatrix}$ だから、
$E=E_0$ の直線上 $y=\pm x$ の上の 原点から距離 $t$ の点 $\frac{1}{\sqrt{2}}\begin{pmatrix}t\\\pm t\end{pmatrix}$ において $\bm \nabla E=\begin{pmatrix}\sqrt{2}t\\\mp\sqrt{2}t\end{pmatrix}$ となって、
$$\rho(E_0)\propto\int_{-\infty}^{\infty}|\nabla E|^{-1}dt=\int_{-\infty}^{\infty}\frac{dt}{2|t|}=+\infty$$
のように発散する。
モンテカルロじゃなくても計算できるか?†
電子状態密度を上記のデルタ関数を用いた形で Mathematica に与えても、
LANG:mathematica
rho[e_] :=
Integrate[Integrate[
DiracDelta[Abs[Fk[{x, y}]] - e],
{x, 0, y/Sqrt[3]}],
{y, 0, 2 Pi/Sqrt[3]}
]
Mathematica はうまく扱えないみたいだった。
三角格子の分散関係を加える†
正確には、上記のまさにグラフェンらしい分散関係に、単純三角格子の分散関係を足す必要がある。 ($\tilde\alpha$ は定数なので無視する)
$$E(\bm k)=\pm\gamma|f_{\bm k}| + E_\mathrm{tri}(\bm k) - \tilde\alpha$$
単純三角格子の時の方が原子間距離が $\sqrt{3}$ 倍遠いので、 単純計算ではクーロン相互作用が $1/3$ になる。 原子が複数いる場合には遮蔽効果によりクーロン相互作用はより急峻に減衰するため。 実際にはさらに影響は小さいと考えられる。
実際に相互作用がどのくらい違うかよく分からないまま、 とりあえず 1/10 だけ、単純三角格子の効果を入れたところ、次のようになった。
Plot3D[{honeycomb[{x, y}]/10 + Abs[Fk[{x, y}]],
honeycomb[{x, y}]/10 - Abs[Fk[{x, y}]]}, {x, 2 Pi 2/3 - 1,
2 Pi 2/3 + 1}, {y, -1, 1}, ViewPoint -> Left, ImageSize -> Large,
PlotPoints -> 101, BoxRatios -> Automatic, MeshFunctions -> {#3 &}]
ガンマ点での高さや有効質量の絶対値が正側と負側とで異なる
一方、K点付近では正側・負側の非対称性は小さく見える。
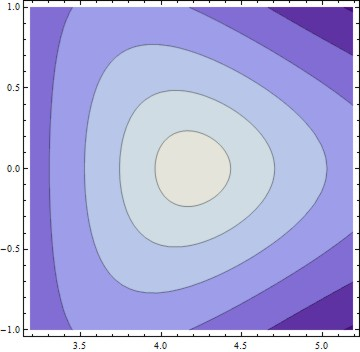
ContourPlot[
honeycomb[{x, y}]/10 + Abs[Fk[{x, y}]] -
honeycomb[{2 Pi 2/3, 0}]/10,
{x, 2 Pi 2/3 - 1, 2 Pi 2/3 + 1}, {y, -1, 1}]
ContourPlot[
honeycomb[{x, y}]/10 - Abs[Fk[{x, y}]] -
honeycomb[{2 Pi 2/3, 0}]/10,
{x, 2 Pi 2/3 - 1, 2 Pi 2/3 + 1}, {y, -1, 1}]
左が正側、右が負側
このようにプロットしてみると、コーンの裾の部分は完全な丸じゃなくて丸まった三角形になることがよく分かる。
コーンの中心部分は円錐になっている。
ContourPlot[
honeycomb[{x, y}]/10 + Abs[Fk[{x, y}]] -
honeycomb[{2 Pi 2/3, 0}]/10,
{x, 2 Pi 2/3 - 0.1, 2 Pi 2/3 + 0.1}, {y, -0.1, 0.1}]
Dirac 方程式†
K 点周りの解†
理想的なグラフェンでは2枚のバンドのうち下のバンドのみが電子で埋まっていて、 ちょうどディラックコーンの先端部分に「フェルミ点」が来る。
このディラックコーン付近の波動関数を記述する方程式は質量のない Dirac 方程式になることを以下確かめる。
上記の、
$$ \begin{pmatrix} 0&-\gamma f_{\bm k}^*\\ {}-\gamma f_{\bm k}&0\\ \end{pmatrix} \begin{pmatrix}C_A\\C_B\end{pmatrix} =\big(E-E_\mathrm{tri}(k)+\tilde\alpha\big)\begin{pmatrix}C_A\\C_B\end{pmatrix} $$
に現れる $f_k$ について、K 点周りの様子を知るため、 $\bm k-\bm K=\delta \bm k$ と書くことにして、 $\delta \bm k$ の一次の項までを残そう。 (長波長近似:$\delta \bm k$ に相当する振動が長波長になる条件で、格子定数分の座標変化に対する係数の変化分を1次の微係数のみで表して議論する)
$$f_k^*=\sum_{l=1}^3 e^{i\bm k\cdot\Delta\bm R_l}$$
より、
$$ \begin{aligned} f_k &=\sum_{l=1}^3 e^{-i\bm k\cdot\Delta\bm R_l}\\ &=\sum_{l=1}^3 e^{i\bm K\cdot\Delta\bm R_l}e^{-i\delta\bm k\cdot\Delta\bm R_l}\\ &=\sum_{l=1}^3 e^{i\bm K\cdot\Delta\bm R_l}(\cancel{1}-i\delta\bm k\cdot\Delta\bm R_l+\dots)\\ &\sim-i\delta\bm k\cdot\sum_{l=1}^3 \Delta\bm R_l e^{i\bm K\cdot\Delta\bm R_l}\\ &=-i\delta\bm k\cdot\frac{\sqrt 3}{2}a\begin{pmatrix} i\\1 \end{pmatrix}\\ &=\frac{\sqrt 3}{2}a(\delta k_x-i\delta k_y) \end{aligned} $$
ただしここで $a$ は格子定数であり、 $\sum_{l=1}^3 e^{i\bm K\cdot\Delta\bm R}=0$ および $\sum_{l=1}^3 \Delta\bm R e^{i\bm K\cdot\Delta\bm R}=\frac{\sqrt 3}{2}a\begin{pmatrix}i\\1\end{pmatrix}$ の関係を用いた。
LANG:mathematica
In[1]:= tau={0,1/Sqrt[3]}
Out[1]= {0,1/Sqrt[3]}
In[2]:= r=RotationMatrix[2Pi/3]
Out[2]= {{-(1/2),-(Sqrt[3]/2)},{Sqrt[3]/2,-(1/2)}}
In[3]:= tauList={tau, r.tau, r.r.tau}
Out[3]= {{0,1/Sqrt[3]},{-1/2,-1/(2 Sqrt[3])},{1/2,-1/(2 Sqrt[3])}}
In[4]:= k=2 Pi {2/3,0}
Out[4]= {(4 \[Pi])/3,0}
In[5]:= Sum[Exp[I k.tau], {tau, tauList}] // Simplify
Out[5]= 0
In[6]:= Sum[tau Exp[I k.tau],{tau,tauList}] // Simplify
Out[6]= {(I Sqrt[3])/2,Sqrt[3]/2}
In[7]:= Sum[-tau Exp[-I k.tau], {tau, tauList}] // Simplify
Out[7]= {(I Sqrt[3])/2,-Sqrt[3]/2}
さらに、三角格子の分散関係 $E_\mathrm{tri}(k)$ は $K$ 点付近で 停留値をとるため、これを定数と見て $E-E_\mathrm{tri}(k)+\tilde\alpha\to E$ と置きなおすと、
$$ \frac{\sqrt 3}{2}\gamma a\begin{pmatrix} 0&\delta k_x+i\delta k_y\\ \delta k_x-i\delta k_y&0\\ \end{pmatrix} \begin{pmatrix}C_A\\C_B\end{pmatrix} =E\begin{pmatrix}C_A\\C_B\end{pmatrix} $$
ただし、
$$E=\pm\gamma |f_k|=\pm\gamma \frac{\sqrt 3}{2}a|\delta \bm k|$$
$\delta k_x+i\delta k_y=|\delta \bm k|e^{i\phi_{\delta k}}$ と置けば、
$$ \begin{pmatrix}C_A\\C_B\end{pmatrix}\propto \begin{pmatrix} \pm 1\\ e^{i\phi_{\delta k}} \end{pmatrix} $$
が上記方程式の解となる。
つまり、電子の進む方向 $\phi_k$ によって A 原子と B 原子との位相が変わるということ。 (これが反射率の異方性を生んだりするらしい?)
Dirac 方程式が出てくる†
質量のない Dirac 方程式が出てくる気配は、 上記の方程式を次のようにパウリ行列 $\sigma_x,\sigma_y,\sigma_z$ で書き直すことで感じられる。
あーと、どこかで $i$ と $-i$ とが入れ替わってしまったみたい。 本来別にどちらでもよいのだけれど、一般的に扱われるパウリ行列に合わせて、 上記の方程式の $i$ と $-i$ とを入れ替えておく。 (実は $K$ 点と $K'$ 点とで $i$ の符号が変わる)
$$ \begin{aligned} &\frac{\sqrt 3}{2}\gamma a\begin{pmatrix} 0&\delta k_x-i\delta k_y\\ \delta k_x+i\delta k_y&0\\ \end{pmatrix} \begin{pmatrix}C_A\\C_B\end{pmatrix}\\ &=\frac{\sqrt 3}{2}\gamma a\left\{ \begin{pmatrix}0&1\\1&0\end{pmatrix}\delta k_x+ \begin{pmatrix}0&-i\\i&0\end{pmatrix}\delta k_x+ \begin{pmatrix}1&0\\0&-1\end{pmatrix}\cdot 0 \right\} \begin{pmatrix}C_A\\C_B\end{pmatrix}\\ &=\frac{\sqrt 3}{2}\gamma a\big( \sigma_x\delta k_x+ \sigma_y\delta k_x+ \sigma_z\cdot 0 \big) \begin{pmatrix}C_A\\C_B\end{pmatrix}\\ &=\frac{\sqrt 3}{2}\gamma a\big(\bm\sigma\cdot\delta \bm k\big) \begin{pmatrix}C_A\\C_B\end{pmatrix}=E\begin{pmatrix}C_A\\C_B\end{pmatrix}\\ \end{aligned} $$
そこで、両辺に $e^{i\delta\bm k\cdot\bm R}$ を掛けると、
$$ \hbar\delta \bm ke^{i\delta\bm k\cdot\bm R}=\frac{\hbar}{i}\bm\nabla_Re^{i\delta\bm k\cdot\bm R} $$
より、$\delta \bm k=\frac{1}{\hbar}\hat{\bm p}$ におきかえられて、
$$ \frac{\sqrt 3}{2}\frac{\gamma a}{\hbar}\big(\bm\sigma\cdot\hat{\bm p}\big) \begin{pmatrix}C_A\\C_B\end{pmatrix}e^{i\delta\bm k\cdot\bm R} =E\begin{pmatrix}C_A\\C_B\end{pmatrix}e^{i\delta\bm k\cdot\bm R} $$
これは自由な電子に対する一般的な Dirac 方程式、
$$ \Big(i\hbar\frac{\PD}{\PD t}+i\hbar c\sum_{i=1}^3 \alpha_i\frac{\PD}{\PD x^i}-\beta mc^2\Big)\psi=0 $$
で $m=0$ と置いた式と瓜二つである。*3http://members3.jcom.home.ne.j... を参考にした
というのも、Dirac 方程式では
$$\{\alpha_i,\alpha_j\}=0\ \ \ i\ne j$$
$$\{\alpha_i,\beta\}=0$$
$$\alpha_i^2=\beta^2=1$$
を満たすために $\alpha,\beta$ は4次行列になるが、ここでは $\beta$ に対する条件が必要ないため、$\alpha_i$ にパウリ行列を入れるだけで上記の条件を満たせるためである。
このとき、
$$ \frac{\hbar}{-i}\frac{\PD}{\PD t}\psi=c\frac{\hbar}{i}\bm\sigma\cdot\bm\nabla\psi=E\psi $$
として変数分離した
$$ c\frac{\hbar}{i}\bm\sigma\cdot\bm\nabla\phi=E\phi $$
と上記 $\begin{pmatrix}C_A\\C_B\end{pmatrix}e^{i\delta\bm k\cdot\bm R}$ の方程式とがまったく同じ形をしている。
つまり $\begin{pmatrix}C_A\\C_B\end{pmatrix}e^{i\delta\bm k\cdot\bm R}$ は質量のない自由粒子に対する Dirac 方程式の定常状態の解になっている。
以下、
$$ \begin{pmatrix}C_A\\C_B\end{pmatrix}e^{i\delta\bm k\cdot\bm R}= \begin{pmatrix}F_A\\F_B\end{pmatrix} $$
と書く。
$F_A,F_B$ の意味†
$$ \begin{aligned} \ket{\Phi} &=\frac{C_A}{\sqrt N}\sum_{\bm R_A}e^{i\bm k\cdot\bm R_A}\ket{\bm R_A}+ \frac{C_B}{\sqrt N}\sum_{\bm R_B}e^{i\bm k\cdot\bm R_B}\ket{\bm R_B}\\ &=\frac{C_Ae^{i\bm k\cdot\bm R}}{\sqrt N}\sum_{\bm R_A}e^{-i\bm k\cdot(\bm R-\bm R_A)}\ket{\phi(\bm R-\bm R_A)}+ \frac{C_Be^{i\bm k\cdot\bm R}}{\sqrt N}\sum_{\bm R_B}e^{-i\bm k\cdot(\bm R-\bm R_B)}\ket{\phi(\bm R-\bm R_B)}\\ &=e^{i\bm k\cdot\bm R}\Bigg(\frac{C_A}{\sqrt N}\sum_{\bm R_A}e^{-i\bm k\cdot(\bm R-\bm R_A)}\ket{\phi(\bm R-\bm R_A)}+ \frac{C_B}{\sqrt N}\sum_{\bm R_B}e^{-i\bm k\cdot(\bm R-\bm R_B)}\ket{\phi(\bm R-\bm R_B)}\Bigg)\\ \end{aligned} $$
の括弧内が周期関数になるから、$\Phi$ がブロッホ関数である、というのが基本の話。
$\bm k\sim\bm K$ のとき、$e^{i\bm k\cdot\bm R}$ は隣り合う基本単位胞でほぼ位相が $\pi$ だけ回るから、 隣り合う基本単位胞で波動関数の符号が反転する。
$\bm K$ を別にしてやると、$e^{i(\bm k-\bm K)\cdot\bm R}=e^{i\delta \bm k\cdot\bm R}$ はゆっくりと変化する関数となるが、残りの部分は基本単位胞2つで元に戻る、周期が二倍の関数になる。
$$ \ket{\Phi} =e^{i\delta\bm k\cdot\bm R}\Bigg(\frac{C_A}{\sqrt N}e^{i\bm K\cdot\bm R}\sum_{\bm R_A}e^{-i\bm k\cdot(\bm R-\bm R_A)}\ket{\phi(\bm R-\bm R_A)}+ \frac{C_B}{\sqrt N}e^{i\bm K\cdot\bm R}\sum_{\bm R_B}e^{-i\bm k\cdot(\bm R-\bm R_B)}\ket{\phi(\bm R-\bm R_B)}\Bigg) $$
この $e^{i\delta \bm k\cdot\bm R}$ と $C_A,C_B$ をまとめたのが $F_A,F_B$。 こいつに対してなら長波長近似が使えるよ、という話なのだと思う。
ワイル方程式†
非相対論的な、普通の Dirac 方程式では
$$ \alpha_i=\begin{pmatrix} 0&\sigma_i\\ \sigma_i&0 \end{pmatrix}, \ \beta=\begin{pmatrix} 0&\bm 1\\ {}-\bm 1&0 \end{pmatrix} $$
と取ることが多いが、これは $|\bm p|\ll m$ のときに方程式が対角形になるようにする配慮だった。 *4http://osksn2.hep.sci.osaka-u....
上記の条件を満たす $\alpha_i,\beta$ はこの他にもいろいろ考えられる。
質量のない Dirac 方程式は逆に $|\bm p|\gg m$ の極限と考えられ、 その場合にはカイラル表示、あるいはワイル表示と呼ばれる表示法が用いられる。
$$\alpha_i=\begin{pmatrix} \sigma_i&0\\ 0&-\sigma_i\\ \end{pmatrix}, \ \beta=\begin{pmatrix} \bm 1&0\\ 0&\bm 1\\ \end{pmatrix}, \ \gamma_i=\beta\bm\alpha_i\begin{pmatrix} 0&-\sigma_i\\ \sigma_i&0\\ \end{pmatrix} $$
たとえばスピン 1/2 で質量がごくわずかしかなく、ほぼ光速で飛び回るニュートリノなどがこの形式で扱われる。
この4成分表示では、
$$ \bm\alpha\cdot\hat{\bm p}\begin{pmatrix} F_A\\F_B\\F'_A\\F'_B \end{pmatrix}=E\begin{pmatrix} F_A\\F_B\\F'_A\\F'_B \end{pmatrix} $$
と書けば $F_A,F_B$ の2成分固有値は $E$、 $F'_A,F'_B$ の2成分固有値は $-E$ となって、 4成分合わせて上下バンドの A, B サイトに関する波動関数を表せることになる。
ここまで来るともはや完全に質量のない Dirac 方程式と言える。
電磁場との相互作用†
$E\to E+e\phi$, $\bm p\to \bm p+e\bm A$ の置き換えをすればよい。 ($\phi$ に空間分布を持たせてしまうと併進対称性が失われて $k$ を元にした議論ができなくなってしまうので、ここでは $\phi=0$ となるようにゲージを取って、電場の影響は $\bm A$ の時間依存性に含めるのがいいというような話を2回目の授業で聞いた)
$$ \begin{aligned} &\pm\bm\alpha\cdot(\hat{\bm p}+e\bm A)\begin{pmatrix} F^\pm_A\\F^\pm_B \end{pmatrix}=\\ &\pm \begin{pmatrix} 0&p_x+eA_x-ip_y-ieA_y\\ p_x+eA_x+ip_y+ieA_y&0\\ \end{pmatrix}\begin{pmatrix} F^\pm_A\\F^\pm_B \end{pmatrix}=(E+e\phi)\begin{pmatrix} F^\pm_A\\F^\pm_B \end{pmatrix} \end{aligned} $$
すなわち、
$$ \begin{cases} \pm(p_x+eA_x-ip_y-ieA_y)F^\pm_B=(E+e\phi)F^\pm_A\\ \pm(p_x+eA_x+ip_y+ieA_y)F^\pm_A=(E+e\phi)F^\pm_B \end{cases} $$
$F^\pm_B$ を消去すると、
$$ \begin{aligned} &(p_x+eA_x-ip_y-ieA_y)(p_x+eA_x+ip_y+ieA_y)F^\pm_A\\ &=\Big\{(p_x+eA_x)^2+(p_y+eA_y)^2+i(p_x+eA_x)(p_y+eA_y)-i(p_y+eA_y)(p_x+eA_x)\Big\}F^\pm_A\\ &=\Big\{(\bm p_\parallel+e\bm A_\parallel)^2+ie(p_xA_y-p_yA_x-A_yp_x+A_xp_y)\Big\}F^\pm_A\\ &=\Big\{(\bm p_\parallel+e\bm A_\parallel)^2+e(\bm\nabla\times\bm A)_z\Big\}F^\pm_A\\ &=\Big\{(\bm p_\parallel+e\bm A_\parallel)^2+e\bm B_z\Big\}F^\pm_A\\ &=(E+e\phi)^2F^\pm_A \end{aligned} $$
$F^\pm_A$ を消去すると、
$$ \begin{aligned} &(p_x+eA_x+ip_y+ieA_y)(p_x+eA_x-ip_y-ieA_y)F^\pm_B\\ &=\Big\{(p_x+eA_x)^2+(p_y+eA_y)^2-i(p_x+eA_x)(p_y+eA_y)+i(p_y+eA_y)(p_x+eA_x)\Big\}F^\pm_B\\ &=\Big\{(\bm p_\parallel+e\bm A_\parallel)^2-ie(p_xA_y-p_yA_x-A_yp_x+A_xp_y)\Big\}F^\pm_B\\ &=\Big\{(\bm p_\parallel+e\bm A_\parallel)^2-e(\bm\nabla\times\bm A)_z\Big\}F^\pm_B\\ &=\Big\{(\bm p_\parallel+e\bm A_\parallel)^2-eB_z\Big\}F^\pm_B\\ &=(E+e\phi)^2F^\pm_B \end{aligned} $$
$\bm\nabla\times\bm A=\bm B$ は磁束密度。$B_z$ はその $z$ 成分。
$F^\pm_A$ と $F^\pm_B$ とで磁場に対する応答が逆になることが分かる。
固有値がエネルギーの2乗になっているところが良くわからないけれど、 磁場をかけるとエネルギーが分裂したり・・・するのかしら???
ヘリシティ†
磁場への応答を見てわかる通り、$F_A,F_B$ は $z$ 方向の疑スピン +1, -1 の状態に対応する。
しかしグラフェン結晶においては上で解いた通り、$F_A,F_B$ の状態に同じだけ電子が入るため、 $z$ 方向の疑スピンの期待値はゼロになる。
一方、$x,y$ 方向の疑スピンは生き残る。その値がいくつになるかを見ておく。
$F_A,F_B$ 成分の相対的な位相は $\bm k$ の向きに依存するのだった。
$$ \begin{pmatrix}F_A\\F_B\end{pmatrix}= \begin{pmatrix}1\\\pm e^{i\phi_{\delta\bm k}}\end{pmatrix} $$
疑スピンの期待値は、
$$ \begin{aligned} \langle\bm \sigma\rangle &=\frac{1}{\sqrt 2}\begin{pmatrix}1&\pm e^{-i\phi}\end{pmatrix}\ \bm\sigma\ \frac{1}{\sqrt 2}\begin{pmatrix}1\\\pm e^{i\phi}\end{pmatrix}\\ &= \frac{1}{2}\begin{pmatrix}1&\pm e^{-i\phi}\end{pmatrix}\Bigg( \begin{pmatrix}0&1\\1&0\end{pmatrix} \ \begin{pmatrix}0&-i\\i&0\end{pmatrix} \ \begin{pmatrix}1&0\\0&-1\end{pmatrix} \Bigg)\begin{pmatrix}1\\\pm e^{i\phi}\end{pmatrix}\\ &= \frac{1}{2}\begin{pmatrix}1&\pm e^{-i\phi}\end{pmatrix}\Bigg( \begin{pmatrix}\pm e^{i\phi}\\1\end{pmatrix} \ \begin{pmatrix}\mp ie^{i\phi}\\i\end{pmatrix} \ \begin{pmatrix}1\\\mp e^{i\phi}\end{pmatrix} \Bigg)\\ &=\begin{pmatrix}\pm \cos\phi&\pm \sin\phi&0\end{pmatrix}\\ \end{aligned} $$
より、$x,y$ 平面内の疑スピンの方向は上バンドでは $\bm k$ 方向、 下バンドでは $-\bm k$ 方向を向く。
Berry 位相・Berry 接続・Berry 曲率†
$\phi_k\to\phi_k+2\pi$ のように $\bm k$ がK点周りを一周したとき、 上記の表式では
$$ \begin{pmatrix}se^{i\phi_{\delta k}+2\pi}\\1\end{pmatrix} =\begin{pmatrix}se^{i\phi_{\delta k}}\\1\end{pmatrix} $$
となって、$\begin{pmatrix}C_A\\C_B\end{pmatrix}$ は元の値に戻る。
ところが、$\begin{pmatrix}C_A\\C_B\end{pmatrix}$ は
$$ \begin{pmatrix} C_A\\C_B \end{pmatrix}=\frac{1}{\sqrt 2}\begin{pmatrix} se^{i\phi_{\delta k}/2}\\e^{i\phi_{\delta k}/2} \end{pmatrix} $$
と書くこともできて、このとき
$$ \frac{1}{\sqrt 2}\begin{pmatrix} se^{i(\phi_{\delta k}+2\pi)/2}\\e^{i(\phi_{\delta k}+2\pi)/2} \end{pmatrix}=\frac{1}{\sqrt 2}\begin{pmatrix} {}-se^{i\phi_{\delta k}/2}\\-e^{i\phi_{\delta k}/2} \end{pmatrix} $$
のように一周回ると符号が反転してしまう。
このあたりの話は Berry 位相と関係している。
Klein tunneling†
質量のない Dirac 方程式からは 自身のエネルギーよりも高い障壁を、透過率1でトンネルする解が得られる。
障壁高さを $V$ として、$0<E<V$ の電子を考える。
この電子は、障壁の外では上側のコーンを、障壁の中では下側のコーンを通過する。
2次元空間で考えるので、障壁は $0<x<D$ として、入射角度を $\phi_k$、 障壁内部での進行方向を $\theta_k$ とする。
入射、出射界面で屈折するので $\theta_k\ne \phi_k$ であることが予想される。
また、それぞれ反射波は $x$ 軸方向のみが折り返されるため、 $\pi-\phi_k,\pi-\theta_k$ となる。
I) $x<0$
$$ \begin{aligned} \begin{pmatrix}C_A\\C_B\end{pmatrix}_\mathrm{I} &=\underbrace{\begin{pmatrix}se^{i\phi_k}\\1\end{pmatrix}e^{ik_x x}e^{ik_y y}}_\text{入射波}\ + \ \underbrace{r\begin{pmatrix}se^{i(\pi-\phi_k)}\\1\end{pmatrix}e^{-ik_x x}e^{ik_y y}}_\text{反射波}\\ &=\underbrace{\begin{pmatrix}se^{i\phi_k}\\1\end{pmatrix}e^{ik_x x}e^{ik_y y}}_\text{入射波}\ + \ \underbrace{r\begin{pmatrix}-se^{i\phi_k}\\1\end{pmatrix}e^{-ik_x x}e^{ik_y y}}_\text{反射波}\\ \end{aligned} $$
II) $0<x<D$
$$ \begin{aligned} \begin{pmatrix}C_A\\C_B\end{pmatrix}_\mathrm{II} =\underbrace{a\begin{pmatrix}se^{i\theta_k}\\1\end{pmatrix}e^{ik'_x x}e^{ik'_y y}}_\text{進行波}\ + \ \underbrace{b\begin{pmatrix}-se^{i\theta_k}\\1\end{pmatrix}e^{-ik'_x x}e^{ik'_y y}}_\text{後退波} \end{aligned} $$
III) $D<x$
$$ \begin{pmatrix}C_A\\C_B\end{pmatrix}_\mathrm{III} =\underbrace{t\begin{pmatrix}se^{i\phi_k}\\1\end{pmatrix}e^{ik_x x}e^{ik_y y}}_\text{透過波} $$
境界条件は界面で連続になること。
$$ \begin{cases} \Phi_\mathrm{I}(0,y)=\Phi_\mathrm{II}(0,y)\\ \Phi_\mathrm{II}(D,y)=\Phi_\mathrm{III}(D,y) \end{cases} $$
さて、一見当然のように思えるこの条件はどこからくるのだろう?
$C_A,C_B$ は各原子サイトに置いた原子の波動関数にかける係数だから、 これらの条件がなくても波動関数の連続性は保たれる。当然、その微係数も。 つまり、これらは波動関数の連続性からくる要件ではない。
これは界面に隣接する原子に対応するシュレーディンガー方程式が成り立つようにする条件なのである。
界面の向こう側の原子が、こちら側と異なる係数を持っていたら、界面に隣接する原子に対するシュレーディンガー方程式が変化してしまうでしょ?ということ。
だから、微係数が連続であるという条件は必要ないのである。
ここの話は http://www.nature.com/nphys/journal/v2/n9/full/nphys384.html の論文でも取り扱われていて、そこに出てくる答えは
$$r=2ie^{i\phi_k}\sin(qD)\frac{\sin\phi_k-ss'\sin\theta}{ss'[e^{iqD}\cos(\theta-\phi)+e^{-iqD}\cos(\theta+\phi)]-2i\sin(qD)}$$
$$\theta=\tan^{-1}\left(\frac{k_y}{q}\right)$$
上記の境界条件から自分でも解いてみる。まずそれぞれの領域の分散関係から、
$$\varepsilon=\gamma\sqrt{k_x^2+k_y^2}$$
に対して、
$$\varepsilon=\gamma\sqrt{q^2+k_y^2}+V$$
より、
$$q=\sqrt{(\varepsilon-V)^2/\gamma^2-k_y^2}$$
条件式は4つ出てくる。
$$\left\{\begin{array}{l} 1+r=a+b\\ se^{i\phi}-sre^{-i\phi}=as'e^{i\theta}-bs'e^{-i\theta}\\ ae^{iqD}+be^{-iqD}=te^{ikD}\\ as'e^{iqD}e^{i\theta}-bs'e^{-iqD}e^{-i\theta}=ste^{ikD}e^{i\phi} \end{array}\right. $$
ここから $a,b,t$ を消去すれば $r$ が求まる。
第1式より $b=-a+(1+r)$
第2式に代入して、
$$ \begin{aligned} &2\cos\phi-(1+r)e^{-i\phi}=2ass'\cos\theta-(1+r)ss'e^{-i\theta}\\ &(1+r)(e^{-i\phi}-ss'e^{-i\theta})=2\cos\phi-2ss'a\cos\theta \end{aligned} $$
第3式を第4式に代入し、さらに第1式を使って、
$$ \begin{aligned} &as'e^{i(qD+\theta)}-bs'e^{-iqD}e^{-i\theta}=se^{i\phi}(ae^{iqD}+be^{-iqD})\\ &2ass'\cos(qD+\theta)-(1+r)ss'e^{-i(qD+\theta)}= 2iae^{i\phi}\sin(qD)+(1+r)e^{i\phi}e^{-iqD}\\ &(1+r)(e^{i\phi}e^{-iqD}+ss'e^{-i(qD+\theta)})= 2a\big(ss'\cos(qD+\theta)-ie^{i\phi}\sin(qD)\big)\\ \end{aligned} $$
両式から $a$ を消去すると、
$$ \begin{aligned} &(1+r)(e^{-i\phi}-ss'e^{-i\theta})=2\cos\phi-ss'\cos\theta (1+r)\frac{e^{i\phi}e^{-iqD}+ss'e^{-i(qD+\theta)}}{ss'\cos(qD+\theta)-ie^{i\phi}\sin(qD)}\\ &(1+r)\left[e^{-i\phi}-ss'e^{-i\theta}+\cos\theta \frac{ss'e^{i\phi}e^{-iqD}+e^{-i(qD+\theta)}}{ss'\cos(qD+\theta)-ie^{i\phi}\sin(qD)}\right]=2\cos\phi\\ &r=2\cos\phi\left[e^{-i\phi}-ss'e^{-i\theta}+e^{-iqD}\cos\theta \frac{ss'e^{i\phi}+e^{-i\theta}}{ss'\cos(qD+\theta)-ie^{i\phi}\sin(qD)}\right]^{-1}-1\\ \end{aligned} $$
似ても似つかないように見えるが、 値を入れて計算してみるとこれで論文の式と等しいらしい。
他の値は、
$$ \begin{aligned} &a=\frac{2\cos\phi-(1+r)(e^{-i\phi}-ss'e^{-i\theta})}{2ss'\cos\theta}\\ &b=-a+(1+r)\\ &t=e^{-ikD}(ae^{iqD}+be^{-iqD})\\ \end{aligned} $$
となる。
反射率を計算してみる†
あまり適当な値を入れると $r>1$ になってしまうので注意が必要。
$(E-V)^2-k_y^2<0$ となる条件では $q$ が虚数になって、 エネルギー障壁中で指数関数的に減衰する解になるから、 そこは別に計算しなければならない。恐らくこれは通常のトンネル条件。
ここでは $(E-V)^2-k_y^2<0$ の領域はプロットしないことにする。
$\gamma=1,s=1,D=1$ で、$V=10,20,30,40,50,100,10000,1000000$ について $|r|^2$ をグラフ化してみた。
障壁高さが高いほど反射率の低い範囲が広がるという不可思議な解が得られる。
論文には方向によって反射率が大きく異なる不思議な形のグラフが書かれているのだけれど、 実はこれは特殊な状況でしか起きない。 特に $V\gg E$ ではあんな風にならないような。
下は $V=50$ の時の反射率を濃淡表示して、同心円を重ねた物。
円の半径が小さいとき、すなわち $E\ll V$ の時は反射率の振動はほぼ同心円状に起きているため、反射率におかしな非等方性は現れない。
一方、$E\sim V$ となる、「ふち」ギリギリを通るような円ではふちのあたりで同心円からずれるために非等方性の強い反射率が得られる。
右は $|k|$ の値を 0 から 30 まで増やしながら、透過率 $|t|^2=1-|r|^2$ を方向に対してプロットした。
これが $V=1000$ になると、 $|r|^2$ の分布がほぼ同心円になることを反映して、 透過率の特異的な非等方性も失われる。
非常に高いエネルギー障壁に対しても、まっすぐ入射する電子は透過確率1で透過する!
また、非常に高いエネルギー障壁に対して $qD$ が $\pi$ の整数倍の時、$\phi$ によらず透過率1になることも出てくる。
エッジの効果†
K点の方程式から $F_B^\pm$ を消去する。
$$ \gamma\begin{pmatrix}0&\hat k_x-i\hat k_y\\\hat k_x+i\hat k_y&0\end{pmatrix} \begin{pmatrix}F_A^\pm(\bm r)\\F_B^\pm(\bm r)\end{pmatrix}= \pm E\begin{pmatrix}F_A^\pm(\bm r)\\F_B^\pm(\bm r)\end{pmatrix} $$
$$ \big(\hat k_x^2+\hat k_y^2\big)F_A^\pm(\bm r)=\frac{E^2}{\gamma^2}F_A^\pm(\bm r) $$
ここから、
$e^{i\bm k\cdot\bm r}$ ただし $k_x^2+k_y^2=\frac{E^2}{\gamma^2}$
が解になる。
$x=\pm\infty,y=\pm\infty$ で有限であることを仮定すれば
$$k_x,k_y\in\mathbb R$$
の平面波が唯一の解になる。このとき当然 $|k_x|<\frac{E}{\gamma}$ にしか解は存在せず、
$$k_y=\pm\sqrt{E^2/\gamma^2-k_x^2}$$
を満たす格子点の数が状態密度に当たる。$E=0$ では状態密度はゼロになる。
一方、系にエッジがあり、たとえば $y>0$ にしか原子が存在しない場合には $y=-\infty$ において波動関数が有限である必要がなくなる。
この時には $y$ の正方向に指数関数的に減衰する解も許される。
これは $k_y$ が虚数の場合に相当して、 $|k_x|>\frac{E}{\gamma}$ にも解が取れることになる。
$$k_y=i\sqrt{k_x^2-E^2/\gamma^2}$$
このような解はエッジから系内部へ指数関数的に減衰する状態を表わし、 エッジ状態と呼ばれる。
$E=0$ では特に、
$$k_y=i|k_x|$$
であり、エッジ状態は $e^{k(ix-y)}$ の形になる。
グラフェンの場合†
$x$ 軸に平行なジグザグエッジではエッジ状態が存在できる。 (もし $y$ 軸に平行ならアームチェアーエッジになるが、 後述の通りアームチェアーエッジではエッジ状態は存在できない)
エッジが水素終端されていると考えて、
$y=0$
に水素原子が並んで、$y>0$ にグラフェンが存在するとすると、 水素原子のサイトは $B$ サイトになる。
水素原子上でのπ電子密度はゼロであるから、
$$F_B(y=0)=0$$
エッジステートは指数関数なので、$F_B(y=0)=0$ ならば $F_B(\bm r)=0$ でなければならない。
一方、$F_A(\bm r)$ は上記の解があり得るから、
$$ \begin{aligned} \begin{pmatrix}F_A(\bm r)\\F_B(\bm r)\\\end{pmatrix} &=C\begin{pmatrix}e^{-|k|y}\\0\end{pmatrix}\theta(y)e^{ikx}\\ &=C\begin{pmatrix}e^{-ky}\\0\end{pmatrix}\theta(k)\theta(y)e^{ikx}\\ \end{aligned} $$
$\theta(y)=\begin{cases}0&y<0\\1&0<y\end{cases}$ はステップ関数。
$x$ 方向の波数の大きい物ほど早く減衰することになる。
このように見ると、エッジ状態が存在するための条件は、
- $F_A,F_B$ の方程式が独立であること
- 片方の原子だけがエッジに接していること
の両方が満たされることである
アームチェアーエッジでは A サイトの原子も B サイトの原子もエッジに接してしまうため、 エッジ状態は存在できない。
量子細線†
この項はグラフェンではない通常の2次元リボン状導体の話。
$y$ 方向の幅が $w$ であるナノリボンでは、
- $x$ 方向に自由 $e^{ik_xx}$
- $y$ 方向に深さ無限大の井戸型ポテンシャル $\sin m\pi y/w$
が解になり、
$$E=\frac{\hbar^2k_x^2}{2m}+\frac{\hbar^2\pi^2}{2mw^2}m^2$$
$$\psi(\bm r)=\sqrt{\frac{2}{wl}}\sin(m\pi y/w)e^{ik_xx}$$
LANG:mathematica
Plot[
Table[x^2 + n^2, {n, 1, 10}], {x, -8, 8},
PlotRange -> {0, 60}, ImageSize -> Large
]
ParametricPlot[
{Sum[If[# > n^2, 1/(2 Sqrt[# - n^2]), 0], {n, 1, 10}] &[x], x},
{x, 0, 60}, PlotRange -> {{0, 3}, {0, 60}}, PlotPoints -> 1000,
AspectRatio -> Full, ImageSize -> {200, 377}
]
グラフェンナノリボン†
ジグザグエッジに挟まれたグラフェンリボンでは、上記の通常のナノリボンの電子状態に加えて、 フェルミレベル付近にエッジ状態が形成されるため、伝導性に大きく寄与するらしい。
$$F_A(\bm r)=(C_1e^{\eta y}+C_2e^{-\eta y})e^{ikx}$$
と置けば、
$$(\hat k_x+i\hat k_y)F_A(\bm r)=\frac{E}{\gamma}F_B(\bm r)$$
より、
$$F_B(\bm r)=\frac{E}{\gamma}(C_1(k+\eta)e^{\eta y}+C_2(k-\eta)e^{-\eta y})e^{ikx}$$
まとめれば、
$$ \begin{pmatrix} F_A(\bm r)\\F_B(\bm r)\\ \end{pmatrix} = C_1\begin{pmatrix} 1\\\gamma(k+\eta)/E \end{pmatrix}e^{ikx+\eta y} + C_2\begin{pmatrix} 1\\\gamma(k-\eta)/E \end{pmatrix}e^{ikx-\eta y} $$
境界条件は $F_B(y=0)=0, F_A(y=w)=0$ より、
$$ \begin{cases} C_1e^{\eta w}+C_2e^{-\eta w}=0\\ C_1(k+\eta)+C_2(k-\eta)=0\\ \end{cases} $$
$C_1=C_2=0$ 以外に解を持つためには、
$$ \begin{vmatrix} e^{\eta w}&e^{-\eta w}\\ k+\eta&k-\eta\\ \end{vmatrix}=0 $$
すなわち、
$$ \begin{aligned} &(k-\eta)e^{\eta w}-(k+\eta)e^{-\eta w}=0\\ &(k-\eta)-(k+\eta)e^{-2\eta w}=0\\ &\underbrace{(k^2-\eta^2)}_{=\,(E/\gamma)^2}-(k+\eta)^2e^{-2\eta w}=0\\ &E=\pm\gamma(k+\eta)e^{-\eta w} \end{aligned} $$
このとき、
$$C_2=-C_1e^{2\eta w}$$
となって、
$$ \begin{aligned} \begin{pmatrix} F_A(\bm r)\\F_B(\bm r)\\ \end{pmatrix} &= Ce^{-\eta w}\begin{pmatrix} 1\\\gamma(k+\eta)/E \end{pmatrix}e^{ikx+\eta y} {}-Ce^{\eta w}\begin{pmatrix} 1\\e^{-2\eta w}\gamma(k+\eta)/E \end{pmatrix}e^{ikx-\eta y}\\ &=C\begin{pmatrix} (e^{\eta(y-w)}-e^{-\eta(y-w)})/2\\ (e^{\eta y}-e^{-\eta y})/2\cdot e^{-\eta w}\gamma(k+\eta)/E \end{pmatrix}e^{ikx}\\[-4mm] &\hspace{34mm}\underbrace{\hspace{20mm}}_{=\,|E|}\\ &=\begin{cases} C\begin{pmatrix} \sinh[\eta(y-w)]\\ \pm\sinh[\eta y] \end{pmatrix}e^{ikx}&|E|<\gamma|k|\\[5mm] C\begin{pmatrix} \sin[\eta'(y-w)]\\ \pm\sin[\eta' y] \end{pmatrix}e^{ikx}&|E|>\gamma|k|\\ \end{cases} \end{aligned} $$
ただし、$\eta=i\eta'$ として $\eta'$ を導入した。
通常であれば後者の条件を満たし、さらにリボンの両端で固定端条件を満たすもののみが解となり、 $\eta$ は離散化するが、グラフェンでは片側のみ固定して反対側はフリーな解が存在するため、 前者の条件や、後者でもリボン幅が波長の半整数倍にならないものも解として成立する。
そのような例を挙げれば次のようになる。
LANG:mathematica
With[{\[Eta] = 4},
Plot[{-Sinh[\[Eta] (y - 1)], Sinh[\[Eta] y]}, {y, 0, 1},
PlotRange -> Full, ImageSize -> Small]]
With[{\[Eta] = 7},
Plot[{-Sin[\[Eta] (y - 1)], Sin[\[Eta] y]}, {y, 0, 1},
PlotRange -> Full, ImageSize -> Small]]
分散関係は、
$\eta=\sqrt{k^2-E^2/\gamma^2}$ より、
$$ E=\pm\gamma(k+\sqrt{k^2-E^2/\gamma^2})e^{-w\sqrt{k^2-E^2/\gamma^2}} $$
変形すると、
$$ \begin{aligned} &E=\pm\gamma(k+\sqrt{k^2-E^2/\gamma^2})e^{-w\sqrt{k^2-E^2/\gamma^2}}\\ &\pm (E/\gamma)e^{w\sqrt{k^2-E^2/\gamma^2}}-k=\sqrt{k^2-E^2/\gamma^2}\\ &\Big[\pm (E/\gamma)e^{w\sqrt{k^2-E^2/\gamma^2}}-k\Big]^2=k^2-E^2/\gamma^2\\ &(E/\gamma)^2e^{2w\sqrt{k^2-E^2/\gamma^2}}\pm (2kE/\gamma)e^{w\sqrt{k^2-E^2/\gamma^2}}+\not\!k^2=\not\!k^2-E^2/\gamma^2\\ &(E/\gamma)\Big(1+e^{2w\sqrt{k^2-E^2/\gamma^2}}\,\Big)=\pm 2ke^{w\sqrt{k^2-E^2/\gamma^2}}\\ &(E/\gamma)\cosh\big(w\sqrt{k^2-(E/\gamma)^2}\,\big)=\pm k\\ &(E/k\gamma)\cosh\big(wk\sqrt{1-(E/k\gamma)^2}\,\big)=\pm 1\\ \end{aligned} $$
$k$ を変化させながら $E$ の関数として左辺の値をグラフにした。 $\pm 1$ との交点が解になる。
LANG:mathematica
Table[Plot[{(E/k) Cosh[k Sqrt[1 - (E/k)^2]], -1, 1}, {E, 0, 40},
PlotRange -> {-10, 10}], {k, -40, 40}] // Export["graphene-ribbon.gif", #] &
分散関係をグラフ化すると、
LANG:mathematica
ContourPlot[{k == x Cosh[Sqrt[k^2 - x^2]], -k ==
x Cosh[Sqrt[k^2 - x^2]]}, {k, -40, 40}, {x, -40, 40}, PlotPoints -> 800]
横軸に $kw$、縦軸に $E/\gamma$ を取っている。 とりあえずここでは $w=1$
グラフは $+k,-k$ それぞれについて点対称で、 互いに $x$ 軸対称であるように見えるのだけれど・・・ 本来は上下に対称でエッジ状態は $K$ 点で右、$K'$ 点で左だけに伸びるとか、 左右は青と黄色のどちらかだけが出るらしいのだけれど、どこを間違えたのか。 右に伸びるか左に伸びるかは境界条件次第で変わるらしく、ジグザグエッジではなくクラインエッジと呼ばれる、ジグザグの外にもう1つだけ原子を付け加えたエッジで挟んだ場合にはエッジ状態の伸びる向きが変わるそうなので、境界条件のところを後で見直してみたい。片方をジグザグ、もう片方をクラインエッジにすると、フラットなバンドが現れるとか。
$E=\pm k$ の解は本当は許されないのだけれど、 ここでは手抜きをしているためプロットに現れてしまっている。
$x$ 軸に沿って出ているヒゲがエッジ状態の解に相当する。
$E/\gamma=k$ の中に入っちゃってるように見えるけれど、 同じヒゲの上の点でもコーンの外だけがエッジ状態である。
グラフ全体を見ると、件のヒゲが $x$ 軸の正の無限大から $x$ 軸に沿って原点付近にやってきて、コーンのへりを通って 左上遠方へと続いていく。で、次は左上遠方から原点付近に戻ってきて 右上遠方へ去っていく、そして右上遠方から戻ってきて・・・・
となっていて、グラフはまるっきり左右対称ではない。
DOS は、
LANG:mathematica
Ew\[Gamma] =
Function[k,
DeleteDuplicates[
Round[#, 0.0001] & /@
Table[x /.
FindRoot[(x/k) Cosh[k Sqrt[1 - (x/k)^2]] == 1, {x,
x0}][[1]], {x0, 0, 20, 0.1}]] //
Select[#, Function[x, 0 < x]] &];
points = Table[{k, #} & /@ Ew\[Gamma][k], {k, -20, 20, 0.1}] // Flatten[#, 1] &;
Show[Plot[{x, -x}, {x, -20, 20}, PlotStyle -> {{Gray, Dashed}}],
ListPlot[points //
Select[#, Function[p, Abs[Abs[p[[1]]] - p[[2]]] > 0.0001]] &,
PlotRange -> {-0.4, 20}],
AspectRatio -> 1, ImageSize -> Medium]
Histogram[
points //
Select[#, Function[p, Abs[Abs[p[[1]]] - p[[2]]] > 0.0001 && p[[2]] < 20]] & //
Map[#[[2]] &, #] &,
{0, 20, 0.2}]
通常のナノリボンと同様に、非対称な放物線の先端で DOS は発散し、エネルギーの絶対値の大きい側へ尾を引く。
グラフェン小片に対する方程式を愚直に解いてみる†
三角形の島†
行列を作るために番号付けを考える。
左下から順に数えるには、行列の指数を $p$ とすると、
$$ \begin{aligned} p&=(n+m+B?)(n+m+1)+n\\ &=(k+B?)(k+1)-1+n \end{aligned} $$
逆変換は、
$k=\mathrm{Floor}\big[\big(\sqrt{1+4p}-1\big)/2\big]$
$B?=p-k(k+1)\ge k+1$
$n=p-(k+B?)(k+1)$
$m=k-n$
で大体あっているのだけれど、 最終ラインのみ $n=0$ が欠番になるので、 一辺を $l$ とすると、
$$ \begin{aligned} p&=(n+m+B?)(n+m+1)+n-(m+n=l)?\\ &=(k+B?)(k+1)-1+n-(k=l)? \end{aligned} $$
$k=\mathrm{Floor}\big[\big(\sqrt{1+4p}-1\big)/2\big]$
$B?=p-k(k+1)\ge k+1$
$n=p-(k+B?)(k+1)+(k=l)?$
$m=k-n$
原子数は $l^2+2l-2$ になる。
相互作用は、
$B_{mn}$ と $A_{mn},A_{(m+1)n},A_{(m+1)(n+1)}$ の間にあるから、
LANG:mathematica
(* mn と p との変換 *)
mn2p[m_, n_, b_, l_] := (m + n + If[b, 1, 0]) (m + n + 1) + n - If[m + n == l, 1, 0];
p2mn[p_, l_] := Module[{k, m, n, b},
k = Floor[1/2 (Sqrt[1 + 4 p] - 1)];
b = p - k (k + 1) >= k + 1;
n = p - (k + If[b, 1, 0]) (k + 1) + If[k == l, 1, 0];
m = k - n;
{m, n, b, k}
];
(* 島の内部かどうかを判定 *)
island[m_, n_, b_, l_] :=
(0 <= m && 0 <= n && m + n <= l) &&
! (!b && ((m == 0 && n == 0) || (m == l && n == 0) || (m == 0 && n == l)))
(* xy 座標に直す *)
mn2xy[m_, n_, b_] := {
m + If[b, 1/2, 0] + n/2,
n Sqrt[3]/2 + If[b, 1/(2 Sqrt[3]), 0]
}
p2xy[p_, l_] := Module[{m, n, b, dummy}, {m, n, b, dummy} = p2mn[p, l]; mn2xy[m, n, b]]
(* 一辺 l の三角島を表わす行列を作る *)
matrix[l_] :=
Table[p, {p, 1, l (l + 1) + l - 2}] //
Map[
Module[{p=#, m, n, b, dummy, q},
{m, n, b, dummy} = p2mn[p, l];
If[!b, {},
{{m, n}, {m + 1, n}, {m, n + 1}} //
Select[#, island[#[[1]], #[[2]], False, l] &] & //
Map[mn2p[#[[1]], #[[2]], False, l] &, #] & //
Map[{{#1, p} -> -1, {p, #1} -> -1} &, #] & //
Join @@ # &
]
]&, #] & //
Join @@ # & //
SparseArray
(* ボンドを図示する -- sw で表示するボンドの方向を指定する *)
showbonds[l_, sw_] :=
Module[{ll, m, lines, bondexists, bond2line},
ll = l^2 + 2 l - 2;
m = matrix[l];
bondexists[{p1_, p2_}] := m[[p1, p2]] != 0 && If[sw, p1 < p2, p1 > p2];
bond2line[{p1_, p2_}] := Line[{p2xy[p1, l], p2xy[p2, l]}];
Table[{p1, p2}, {p1, 1, ll}, {p2, 1, ll}] //
Flatten[#,1] & //
Select[#, bondexists]& //
Map[bond2line, #] & //
Graphics
]
(* 固有値問題を解いて結果をエネルギーの小さい純に並び替える *)
solve[l_] :=
Eigensystem[matrix[l] // N] //
SortBy[Transpose[{#[[1]] // N, #[[2]]}], First] & //
Transpose
(* 固有値問題を解いて結果をエネルギーの小さい純に並び替え、さらに正規直交化する *)
solveandorthogonalize[l_] :=
solve[l] //
Transpose //
Gather[#, #1[[1]]==#2[[1]] &] & //
Map[Function[eigenspace,
Orthogonalize[Map[Last, eigenspace]] //
Map[{eigenspace[[1]][[1]], #}&, #] &
], #] & //
Flatten[#, 1] & //
Transpose
(* 正規直交化されていることを確認する *)
checkorthogonal[solution_] := Module[{l = atoms2l[solution[[1]]//Length]},
Table[
solution[[2]][[n]].solution[[2]][[m]],
{n, 1, l^2 + 2 l - 2}, {m, 1, l^2 + 2 l - 2}] //
Chop //
MatrixForm
]
(* エネルギー固有値をグラフにする *)
showenergies[solution_] :=
ListPlot[ solution[[1]],
ImageSize->Medium, PlotMarkers->{Automatic,Medium},
BaseStyle->{FontSize->20}, PlotRange->{-3,3}]
(* 原子数から l を求める *)
atoms2l[atoms_] := -1 + Sqrt[3 + atoms]
(*n 番目の固有状態を原子の座標と値の組に変換する*)
points[vector_] := Module[{l = atoms2l[vector // Length]},
Table[Append[p2xy[p, l], vector[[p]]], {p, 1, l^2 + 2 l - 2}] ~Join~
( Join[ (*周囲の点を追加する*)
{{0, 0, False}, {l, 0, False}, {0, l, False}},
Table[{mm, -1, True}, {mm, 1, l - 1}],
Table[{-1, nn, True}, {nn, 1, l - 1}],
Table[{l - nn, nn, True}, {nn, 1, l - 1}]
] //
Map[Append[mn2xy[#[[1]], #[[2]], #[[3]]], 1/2] &, #] &
)
]
normalize[vector_] := Module[{ma = Max[vector // N // Abs]}, (vector/ma + 1)/2];
showsolution[vector_, title_] :=
Module[{l = atoms2l[vector // Length]},
ListDensityPlot[ points[vector // N // normalize],
Frame -> False, ImageSize -> Tiny, PlotLegends -> Placed[title, Below],
InterpolationOrder -> 0, PlotRange -> {{-0.1, l + .1}, {-0.6, l - 0.4}, {0, 1}},
ColorFunctionScaling -> False,
ColorFunction -> Function[v,
If[v < 1/4, Blend[{Purple // Darker, Blue // Lighter}, 4 v],
If[v < 1/2, Blend[{Blue // Lighter, White}, 4 (v - 1/4)],
If[v < 3/4, Blend[{White, Yellow // Lighter}, 4 (v - 1/2)],
Blend[{Yellow // Lighter, Red}, 4 (v - 3/4)]]]]]
]
]
showallsolutions[solution_] :=
Module[{l = atoms2l[solution[[1]] // Length]},
Table[showsolution[solution[[2]][[n]], n], {n, 1, l^2 + 2 l - 2}] //
TableForm[Partition[#, 10, 10, 1, {}]] &]
showlocaldos[solution_, fromto_] :=
Module[{l = atoms2l[solution[[1]] // Length]},
Map[
If[Length[#1] == 0,
showsolution[solution[[2]][[#1]]^2, ToString[#1]],
If[Length[#1] == 1,
showsolution[solution[[2]][[#1[[1]]]]^2, ToString[#1[[1]]]],
showsolution[Sum[solution[[2]][[n]]^2, {n, #1[[1]], #1[[2]]}],
ToString[#1[[1]]] <> " ~ " <> ToString[#1[[2]]]]
]
] &, fromto]
] // TableForm[Partition[#, 10, 10, 1, {}]] &
$l=2$†
LANG:mathematica matrix[2] // MatrixForm
$$ \left( \begin{array}{cccccc} {} 0 & -1 & -1 & 0 & 0 & 0 \\ {} -1 & 0 & 0 & -1 & 0 & 0 \\ {} -1 & 0 & 0 & 0 & -1 & 0 \\ {} 0 & -1 & 0 & 0 & 0 & -1 \\ {} 0 & 0 & -1 & 0 & 0 & -1 \\ {} 0 & 0 & 0 & -1 & -1 & 0 \\ \end{array} \right) $$
全部で6原子からなる島。 各行・列がそれぞれの原子に相当する。 ボンドで結ばれている部分に -1 が入っている。
LANG:mathematica
With[{l = 2}, {showbonds[l, True], showbonds[l, False]}]
LANG:mathematica solution = solveandorthogonalize[2]; showenergies[solution]
ボンドを可視化すると、原子が正しく結ばれていることを確認できる。
これを解くと非重複解が2つ、2重解が2つの合計6個の固有値が求まる。 この数は原子数に一致する。
LANG:mathematica showallsolutions[solution]
固有状態はこの通り。
E > 0 の解は、-E の解を互い違いに符号反転させたものになっている。
n = 1 と n = 6 は固有状態自体が3回対称を持つから良いとして、
縮退している n = 2,3 と n = 4,5 について、
- 縮退している相手と似てないこと
- 自身を120度回した形と縮退しているはずなのにそのような解が現れないこと
が気になる。
実は、自身を120度回した解は、縮退した2つの固有状態の線形結合で作ることができる。
LANG:mathematica
{{solution[[2]][[2]], "\!\(\*SubscriptBox[\(u\), \(2\)]\)"},
{(-solution[[2]][[2]] + Sqrt [3] solution[[2]][[3]])/2,
"(\!\(-\*SubscriptBox[\(u\), \\(2\)]\)+\!\(\*SqrtBox[\(3\)]\)\!\(\*SubscriptBox[\(u\), \\(3\)]\))/2"},
{(-solution[[2]][[2]] - Sqrt[3] solution[[2]][[3]])/2,
"(\!\(-\*SubscriptBox[\(u\), \\(2\)]\)-\!\(\*SqrtBox[\(3\)]\)\!\(\*SubscriptBox[\(u\), \\(3\)]\))/2"}
} // Map[(showsolution @@ #) &, #] & // Grid[{#}] &
LANG:mathematica
{{solution[[2]][[3]], "\!\(\*SubscriptBox[\(u\), \(3\)]\)"},
{(-Sqrt[3] solution[[2]][[2]] - solution[[2]][[3]])/Sqrt[5],
"(\!\(-\!\(\*SqrtBox[\(3\)]\)\*SubscriptBox[\(u\), \\(2\)]\)-\!\(\*SubscriptBox[\(u\), \(3\)]\))/2"},
{(Sqrt[3] solution[[2]][[2]] - solution[[2]][[3]])/Sqrt[5],
"(\!\(\!\(\*SqrtBox[\(3\)]\)\*SubscriptBox[\(u\), \\(2\)]\)-\!\(\*SubscriptBox[\(u\), \(3\)]\))/2"}
} // Map[(showsolution @@ #) &, #] & // Grid[{#}] &
また、1番目と6番目の波動関数の局所状態密度は一様であり、 縮退している2番目と3番目、4番目と5番目の波動関数の存在確率の和も一様であった。 (いたるところ一定)
LANG:mathematica
showlocaldos[solution, {1, {2, 3}, {4, 5}, 6}]
$l=3$ 原子数 13†
今度は重複度3の解が出てくる。
- n=1 の解は中央に1つだけ山を持つ
- n=2, 3 の解は中央に節があって、山と谷がある
- n=4 の解は2つの節がある
- n=5,6 の解はわかりづらいけれど、混ぜると n=9 の解を互い違いに反転させたものが得られるはずで、縦と横に1つずつ節を持つ
- n=7 の解はエッジ状態で、片方のエッジで値を持ち、反対側へ減衰する
- n>7 の解は n<7 の解を互い違いに反転させた形になっている
$l=5$ 原子数 33†
l=3 の時と同様に、
- E<0 では徐々に節の数が増えていき
- E=-1 では n=11 のような特徴的な解が現れる
- E=0 はエッジ状態
- E>0 では E<0 の解を互い違いに反転したもの
- E=1 では n=21 のような特徴的な解が現れる
になっている。
$l=8$ 原子数 78†
$l=40$ 原子数 1678†
DOS を求めてみると、
グラフェンそのものの DOS に近づいてきていることが分かる。
ただし、エッジ状態に相当する、E=0 のピークが存在する。
この E=0 の状態を抜き出してみると、
確かにエッジ状態っぽい。
ここで作った三角形の島ではすべてのエッジがジグザグエッジになるため、 例の特徴的なエッジ状態が見られることが確認できる。
E=0 に隣接する状態が、K 点や K' 点周辺の状態である。
E < 0 は、
E > 0 は、
隣り合うサイトで符号が入れ替わる細かい振動を除いて k の値が徐々に増えていく感じになっていて、 固定端の条件によりエネルギーが離散化している雰囲気だ。
E = ±1 は M 点に相当する。
E = -1 はこんな感じ。
少し整理しないと何が何やら・・・
$E=1$ と $E=0$ に相当する LDOS を見てみると、
$E=0$ がエッジ状態なのに比べて、$E=1$ は・・・なんなんだろう?
$E=0$ の軌道はほぼ完全に縮退しているように見えて、 $E\ne0$ の軌道との間にエネルギーギャップがあるように見える。 もしかするとこれはジグザグエッジとクラインエッジに挟まれたナノリボンに期待される フラットなエッジ状態バンドが形成されているのと対応しているのかもしれない?
任意形状の島†
自由な形の島を作れるようにする。
大きなハニカムシートを作っておいて、 createisland に与える criteria で島の形状に切り出す。
原子位置と番号との関係は以下の通り。
0,0 番の原子を原点に持ってくると6回対称にならないので、 y 軸方向に少しだけずらしてある。
LANG:mathematica
(* 島を作成する *)
createisland[size_, criteria_] :=
Module[{atoms, bonds, triangles, indices, table, neighbors},
table[n_, m_, b_] = 0;
{atoms, triangles, indices} =
Table[{Sqrt[3] (m + b/2 + Mod[n, 2]/2), (3/2) n + b (1/2), m, n, b},
{m, -size, size}, {n, -size, size}, {b, 0, 1}] //
Flatten[#, 2] & //
Select[#,
Function[xymnb, criteria /. {x -> xymnb[[1]], y -> xymnb[[2]]}]
] & //
MapIndexed[Function[{xymnb, index},
table[xymnb[[3]], xymnb[[4]], xymnb[[5]]] = index[[1]];
{
xymnb[[{1, 2}]],
If[xymnb[[5]] == 1, { {Sqrt[3]/2, 1/2}, {-Sqrt[3]/2, 1/2}, {0, -1} },
{ {Sqrt[3]/2, -1/2}, {-Sqrt[3]/2, -1/2}, {0, 1} }] //
Map[xymnb[[{1, 2}]] + # &, #] &,
xymnb[[{3, 4, 5}]]
}], #] & //
Transpose //
Evaluate;
neighbors[n_, m_, b_] := If[Mod[n, 2] == 0,
If[b == 0, {{m - 1, n - 1}, {m - 1, n}, {m, n}},
{{m, n}, {m, n + 1}, {m + 1, n}}],
If[b == 0, {{m, n - 1}, {m - 1, n}, {m, n}},
{{m, n}, {m + 1, n + 1}, {m + 1, n}}]
];
bonds =
MapIndexed[Function[{mnb, index}, Module[{m, n, b, i},
{m, n, b} = mnb;
i = index[[1]];
neighbors[n, m, b] //
Map[Module[{j = table[#[[1]], #[[2]], 1 - b]},
If[j > 0, {{i, j} -> -1, {j, i} -> -1}, {}]] &, #] &
]], indices] //
Flatten[#, 2] & //
SparseArray;
{size, atoms, bonds, triangles}
]
(* ボンド位置を表示する *)
showbonds[island_, sw_] :=
Module[{atoms, bonds, bondexists, bond2line},
atoms = island[[2]];
bonds = island[[3]];
bondexists[{p1_, p2_}] :=
bonds[[p1, p2]] != 0 && If[sw, p1 < p2, p1 > p2];
bond2line[{p1_, p2_}] := Line[{atoms[[p1]], atoms[[p2]]}];
Table[{p1, p2}, {p1, 1, Length[atoms]}, {p2, 1, Length[atoms]}] //
Flatten[#, 1] & //
Select[#, bondexists] & //
Map[bond2line, #] & //
Graphics
]
showbonds[island_] := Grid[{{ showbonds[island, False], showbonds[island, True] }}]
(* 固有値問題を解いて結果をエネルギーの小さい純に並び替える *)
solve[bonds_] :=
Eigensystem[bonds // N] //
SortBy[Transpose[{#[[1]] // N, #[[2]]}], First] & //
Transpose
(* 固有値問題を解いて結果をエネルギーの小さい純に並び替え、さらに正規直交化する *)
solveandorthogonalize[bonds_] :=
solve[bonds] //
Transpose //
Gather[#, #1[[1]]==#2[[1]] &] & //
Map[Function[eigenspace,
Orthogonalize[Map[Last, eigenspace]] //
Map[{eigenspace[[1]][[1]], #}&, #] &
], #] & //
Flatten[#, 1] & //
Transpose
(* 正規直交化されていることを確認する *)
checkorthogonal[solution_] := Module[{l = atoms2l[solution[[1]]//Length]},
Table[
solution[[2]][[n]].solution[[2]][[m]],
{n, 1, l^2 + 2 l - 2}, {m, 1, l^2 + 2 l - 2}] //
Chop //
MatrixForm
]
(* エネルギー固有値をグラフにする *)
showenergies[solution_] :=
ListPlot[ solution[[1]],
ImageSize->Large, PlotMarkers->{Automatic,Medium},
BaseStyle->{FontSize->20}, PlotRange->Full]
(* 状態を表示する *)
showstate[island_, vector_, title_] :=
Module[{ma, values, color, ymi},
ma = Max[Abs[vector]];
ymi = Min[Transpose[island[[2]]][[2]]];
values = vector/ma/2 + 1/2;
color = Function[{v},
If[v < 1/4, Blend[{Purple // Darker, Blue // Lighter}, 4 v],
If[v < 1/2, Blend[{Blue // Lighter, White}, 4 (v - 1/4)],
If[v < 3/4, Blend[{White, Yellow}, 4 (v - 1/2)],
Blend[{Yellow // Lighter, Red // Darker}, 4 (v - 3/4)]]]]];
island[[4]] //
MapIndexed[Module[{c = color[values[[#2[[1]] ]] ]},
{FaceForm[c], EdgeForm[c], Polygon[#1]}] &, #] & //
Graphics[#, ImageSize -> Small] &
] // Grid[{{#}, {title}}] &
showallstates[island_,solution_] :=
solution[[2]] //
MapIndexed[showstate[island, #1, #2[[1]]] &, #] & //
Grid[Partition[#, 10, 10, 1, {}]] &
showldos[island_, solution_, fromto_] := Map[
If[Length[#1] == 0,
showstate[island, solution[[2]][[#1]]^2, #1],
If[Length[#1] == 1,
showstate[island, solution[[2]][[#1[[1]]]]^2, #1[[1]]],
showstate[island, Sum[solution[[2]][[n]]^2, {n, #1[[1]], #1[[2]]}],
ToString[#1[[1]]] <> " ~ " <> ToString[#1[[2]]]]
]
] &, fromto] // Grid[Partition[#, 10, 10, 1, {}]] &
6角形の島 $n=2$ 原子数 54†
LANG:mathematica
island := With[{n = 2},
createisland[n+2,
Abs[y - 1] < 1.5 n + 1.1 &&
Abs[y - 1 - Sqrt[3] x] < 3 (n + 1) &&
Abs[y - 1 + Sqrt[3] x] < 3 (n + 1)
]
]
showbonds[island]
LANG:mathematica solution = solveandorthogonalize[island[[3]]]; showenergies[solution]
LANG:mathematica showallstates[island, solution]
E=0 にエッジ状態はない。
E=±1は強く縮退している。
6角形の島 $n=10$ 原子数 726†
E=0 は完全には縮退していないものの、K 点付近の状態はやはりエッジ状態になっている。
分布をみる限り、きれいに縮退しない理由は角の部分でつじつまが合わないためにように思える???
一方 E=±1 の鞍点は強く縮退している。
6角形の島 アームチェア 原子数 684†
LANG:mathematica
island := With[{n = 10, ox = 0., oy = 1, dx = 0.5, dy = 0.5},
createisland[n + 3,
Abs[x - ox] < 1.5 ( n + dx ) &&
Abs[x - ox - Sqrt[3] (y - oy)] < 3 (n + dy) &&
Abs[x - ox + Sqrt[3] (y - oy)] < 3 (n + dy)
]
]
アームチェアエッジではゼロ付近の縮退はない。
$E>0$ についてエネルギーの低いほうから LDOS を並べてみた。
LANG:mathematica
showldos[island, solution, {{382, 383}, 384, 385, {386, 387}, {388, 389}, 390, {391, 393}, {394, 395}, {396, 397}, {398, 399}, 400, {401, 402}, {403, 404}, 405, {406, 407}, {408, 409}, 410, 411, 412, {413, 414}, {415, 416}, {417, 420}, {421, 422}, {423, 424}, 425, 426, {427, 428}, {429, 430}, {431, 432}, {433, 434}, {435, 436}, {437, 438}, 439, {440, 441}, 442, {443, 444}, 445, {446, 447}, {448, 449}, 450, {451, 452}, {453, 454}, 455, 456, {457, 458}, 459, {460, 461}, {462, 463}, {464, 465}, 466, {467, 468}, {469, 493}, 494, 495, {496, 497}, {498, 499}, 500, {501, 502}, {503, 504}, 505}]
"469~493" というのが $E=1$ に対応する分布。かなり特徴的なのだけれど、どういう意味があるのだろう?
島のサイズを大きくしてみたところこうなった。Wikipedia:ダイヤモンドゲーム の盤を彷彿とさせる・・・
6角形の島 $n=30$ 原子数 5766†
かなりグラフェンに近づいているが、ゼロ付近に縮退が見られる?
対数プロットしてみると、完全には縮退していないことが分かる。
E>0 の状態をプロットしておく。
両側ジグザグの ナノリボン 原子数†
LANG:mathematica
island := With[{n = 60},
createisland[n+1,
Abs[y - 1] < 1.5 n/10 + 1.1 &&
Abs[y - 1 - Sqrt[3] x] < 5 (n + 1) &&
Abs[y - 1 + Sqrt[3] x] < 5 (n + 1)
]
] // Evaluate
ぴんぴんヒゲが立っているのが量子細線のところで出てきたピークに当たる。
あるモードが現れる最低エネルギーのところで dos が高くなる。
鞍点を超えるとピークから引く裾の方向が逆になる?
E=0 は縮退していない(グラフの縦軸は対数スケール)。 これは6角形の島と同じ。
E>0 の K 点、K' 点付近。
アームチェアエッジ†
真四角の島を作ると上下端をジグザグに、左右端をアームチェアにできる。
LANG:mathematica
island := With[{n = 21},
createisland[n+1,
Abs[y - 1] < 1.5 n/10 + 1.1 &&
Abs[x] < Sqrt[3] (n + 1)
]
] // Evaluate
E>0 の K 点、K' 点付近。
非常にきれいでわかりやすい。
ジグザグエッジにはエッジステートが形成される
(A,B サイトのどちらかしかエッジに接しないため)
アームチェアーエッジにはエッジステートは形成されない
(A,B サイトの両方がエッジに接するため)
位相は隣り合う原子間でほぼ反転する
E = 0 では完全に反転するが、エネルギーが高くなると完全反転から少しずれて、 ゆっくりとした振動が見えるようになる
アームチェアーエッジは固定端なので、横方向の振動はエッジ部分が節になる波数に限られる。
ジグザグエッジは必ずしも固定端になる必要はないので、縦方向の振動の波数は任意のもので構わない。
結果的に、横方向の波数でモードが決まっている。
やってみたい計算†
- 周期境界を入れてみたい
- xy方向の周期境界
- x方向だけの周期境界(ナノリボン(リング?) or ナノチューブに相当)
- 変な周期境界
- 6角形の端で折り返すとか
- 斜めの周期境界(ナノチューブに相当)
- 分散関係を出したい
- 欠陥を入れてみたい
- 電場をかけて電流を計算・・・できるのか?
- 有限島でエッジ状態がフラットになる条件を見たい
*1 http://www1.doshisha.ac.jp/~makato/lecture/IC_S1/eff_mass.pdf を参考にした
*2 演算子のエルミート性については 量子力学Ⅰ/固有値と期待値#qf83b503 を参照のこと
*3 http://members3.jcom.home.ne.jp/nososnd/qu/weyl.pdf を参考にした
*4 http://osksn2.hep.sci.osaka-u.ac.jp/~naga/kogi/konan-class04/ch4-dirac.pdf
添付ファイル: