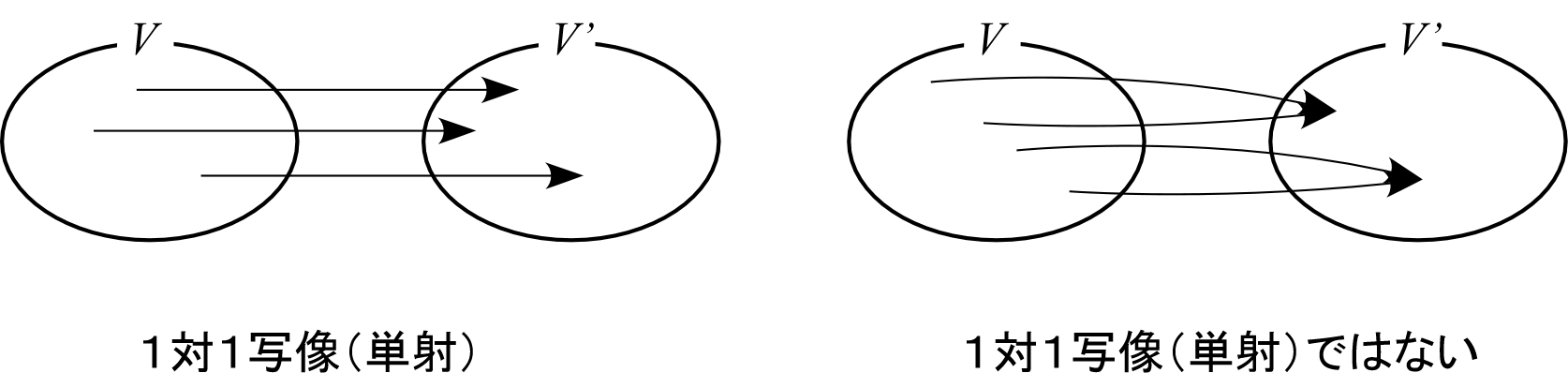前の単元 <<<
線形代数II
>>> 次の単元
写像 †
通常、関数
と言えば実数を実数に、あるいは複素数を複素数に変換する規則のことである。
例えば複素関数
は「
を
に変換する」という規則なので、
によって複素数
は
に変換される。
この考え方を拡張して、ベクトルをベクトルに変換する関数を考えることができる。
例えば2次元列ベクトルを3次元列ベクトルに変換する関数
は、
を、
のように、
に変換する。
この
は2次元列ベクトル空間から3次元列ベクトル空間への「写像」である。
一般に、「集合
から
への写像
」と言えば、
ある集合
の要素を別の集合
の要素に変換する規則のことである。
このことを、
と書く。このとき、
に対して
となる。例えば
は 0 を変換できないため
ではない。
が
を
に変換する規則であることを指して、
という書き方も良く行われる。
2つの矢印
と
との違いに注意せよ。
例:
先の例であれば
であり、
と書ける。これを
のように書くことも多い。
例:
集合
は任意に取れるから、例えば
を、
に対して
と定義すれば、
である。
なので、
と捉えても問題ない。
線形写像 †
を線形空間として、
が次の条件を満たすとき、
は「線形である」と言う。
-
,
に対して、
すなわち、線形写像ではベクトル和やスカラー倍を行ってから
で変換しても、
で変換してからベクトル和やスカラー倍を行っても、同じ結果が得られる。
この性質を、線形写像はベクトル和やスカラー倍に対して透過的である、などともいう。
演習:
(1) 実数関数
は線形か? → つまり、
と
は常に等しいか?
(2) 実数関数
は線形か?
(3) 実数関数
は線形か?
(4)
が
実行列であれば、
は
の写像となる。この写像は線形か?
線形の条件は、
として、
と書いても同値である。
線形写像を大文字のアルファベットで表わすとき、
写像の括弧を省略して行列
とのかけ算のように書くこともよく行われる。
このとき、
-
分配法則が成り立つ
-
スカラー倍との交換法則が成り立つ
-
線形写像同士の交換はできない
つまり数ベクトルと行列との掛け算と同じ扱いができる。
例:
先のように
に対して
と定義すれば、これは線形写像になる。
微分や積分は 典型的な線形写像 として以後頻出する
のように括弧を省略する書き方は
のような書き方と対応している。
こういう場合、
を 「線形演算子」とも呼ぶ。
例:
2次以下の
の多項式の集合を
として、
を
ただし
と定義すれば、これは線形写像になる。
例:
多項式と数ベクトル表現との間の変換、例えば
-
ただし
-
ただし
もそれぞれ線形写像になる。
練習 †
問:
が線形写像であれば、
となることを示せ。
答:
(最後の部分で、任意の
について
となることを使った)
線形代数という学問について †
線形写像 $f:V\to V'$ とは「ベクトルの和とスカラー倍に対して透過的な写像である」と上で説明した。
この説明が意味を持つためには「$V$ と $V'$ とにそれぞれ和とスカラー倍が定義されている必要がある」のは当然であるが重要でもある。
ここまででピンと来た人は感が良い。
和とスカラー倍が定義された集合に「ベクトル空間」あるいは「線形空間」と名前を付け、
それらの要素をベクトルと呼び、その性質を学ぶ線形代数という学問は、
実は線形写像について議論するための学問であったのだ。
線形写像について議論できるギリギリの性質だけを残して他をそぎ落とした公理こそがベクトル空間の公理であることを理解してほしい。
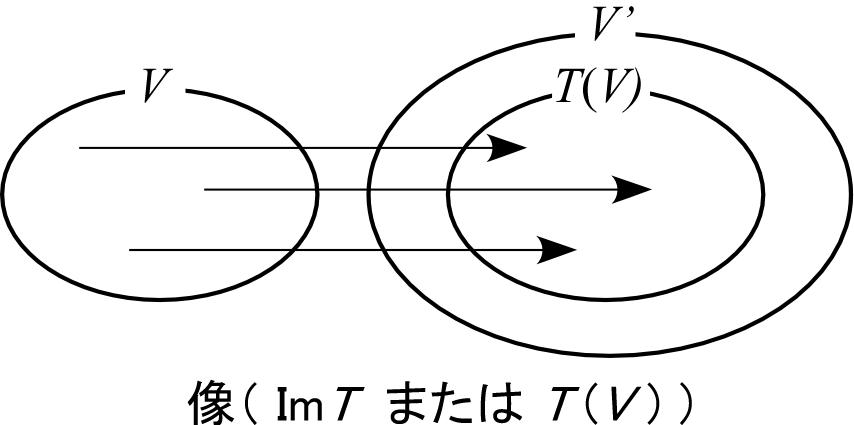
像 $\text{Im}\,T$ †
写像
の「像」は、
として定義される。
上の式は「ある
に対して
が成り立つような
の元
を集めた集合が
である」 と読めて、その意味は
「任意の $\bm x'\in\mathrm{Im}\,T\subset V'$ には、そこに移ってくる元
が存在して、
が成り立つ」ということ。
像は
とも書かれる。当然、
である。
高校で関数について定義域、値域を考えたが、その値域にあたる。
線形写像の像は線形空間となる †
線形空間の部分集合が部分空間となることを示すには、
その集合が演算に対して閉じていることを確かめればよかった。
に対して、
となるような
が存在するから、
すなわち
であり、
はベクトル和とスカラー倍について閉じている。
したがって、
は $V'$ の部分空間となる。
階数 †
ある線形写像
の「階数」は、
として定義される。すなわち像の次元。
行列の階数との関係は後述する。
例:
が
ならば、
であり、
である。
が
ならば、
であり、
である。
性質:
のとき、
となる。
解説:
前者は、
の任意の基底
に対して
が
を張ることと、
であることから証明される。
後者は
が
の部分空間であることから自明。
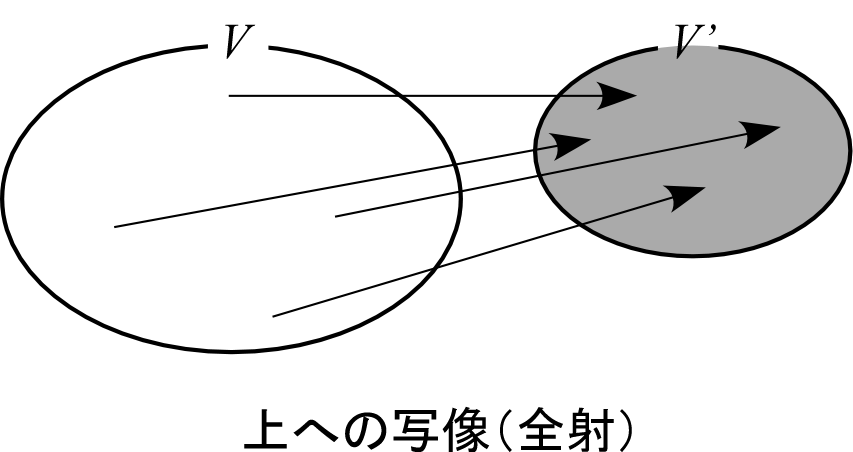
全射(上への写像) †
写像
が
を満たすとき、上への写像あるいは全射であるという。
(教科書の「全写」は間違い)
これは、任意の
に対して、
そこに移ってくる
を必ず見つけられること、
と同義である。
例えば、
は
なら全射ではないが、
なら全射である。
(矢印の右側の大括弧 [ ] はベクトルが張る空間を表わす記号だった)
単射(1対1写像) †
一般の写像では異なるベクトルが同じ値に移される場合があるが、
であれば必ず
であるとき、
つまり異なるベクトルが同じベクトルへ移されることがないとき、
は単射である、あるいは、1対1写像である、という。
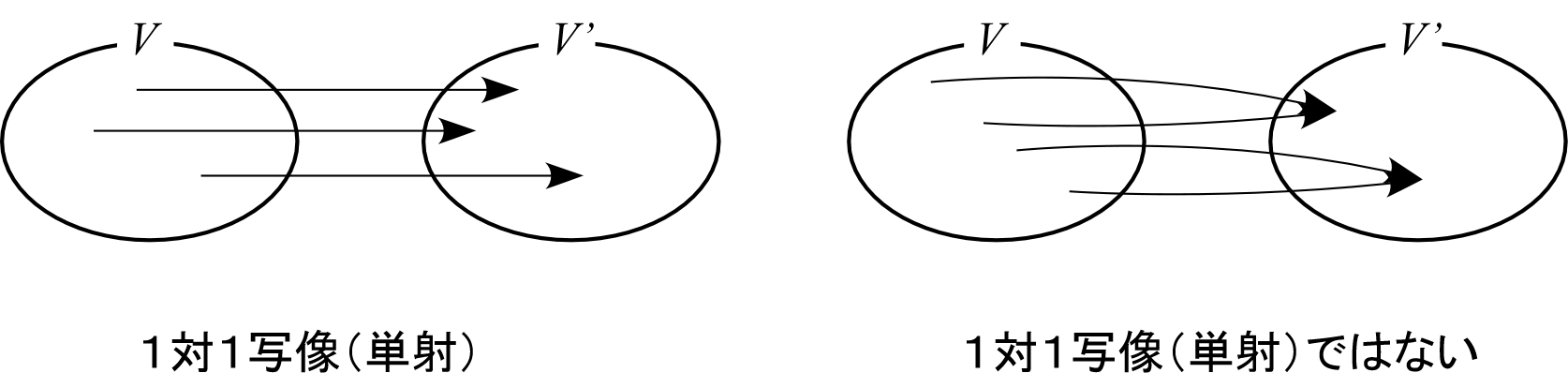
-
と
との間に1対1対応を生む
-
と
との間の1対1ではないことに注意せよ
全単射(上への1対1写像) †
単射かつ全射であることをいう。
の元の1つ1つに
の元が1つ1つ対応することになる。
このときに限り、「逆写像
」が定義できる。
- 全単射でないと逆写像は定義できないことに注意せよ
- 1対1でないと、ある
に複数の
が対応してしまう
- 上への写像でないと、ある
に対応する
が存在しない場合がある
- 逆写像も全単射になり、逆写像の逆写像は元の写像である
全射、単射、全単射のわかりやすい図解 †
https://twitter.com/taketo1024/status/899084595630489601
練習 †
問:
線形写像の逆写像
は線形写像であることを示せ
答:
とすると、
一方、
の両辺に
を作用させると
この左辺は
と等しいことから、
が線形であることが示される。
同型 †
2つの線形空間
と
の間に 全単射の線形写像
を定義できるとき、
と
は同型であるといい、
と書く。
このとき、
を同型写像と呼ぶ。
注)同型である2つの線形空間の間には無数の異なる同型写像を定義可能であるが、
1つでも同型写像を定義できれば同型と呼ぶ。
同型の空間は非常に似た構造を持つ。
-
なら
-
なら
-
が
の基底なら、
は
の基底となる
- などなど、
上の演算はそのまま
上でも(対応する)同じ結果を生む
特に、すべての
上の
次元ベクトル空間は
に同型であるため、1年生でやった
次元数ベクトル空間は、
任意の(有限次元の)線形空間を理解するための基礎となる。
∵ 特定の基底に対して
の元から数ベクトル表現への写像を定義すればそれが同型写像となる。
同値関係 †
線形空間の「同型」は同値関係の公理を満たす。すなわち、
-
: 反射律 (恒等写像による同型)
-
: 対称律 (逆写像による同型)
-
: 推移律 (合成写像による同型)
一方を調べればもう一方が分かる例 †
の同型写像を
とすると、
が線形独立であれば、
も線形独立である。
対偶を証明する。証明するのは、
「
が線形従属ならば、
も線形従属である。」
は従属なので、
すべてがゼロではない3つのスカラー
に対して
が成立する。
は線形なので、
ここで両辺に
を掛けると、
より、
はすべてがゼロではないから、
は線形従属。
同型写像の階数 †
同型写像
の階数は
である。
核 $\text{Ker}\,T$ †
線形写像
の核 (Kernel):
「
でゼロベクトルに移されるベクトルの集合」のこと。
核はゼロを含む †
核は線形空間となる †
に対して、
より、
となる。
すなわち、
はベクトル和とスカラー倍に対して閉じており、
部分空間となる。
1対1写像の条件 †
は、
が1対1写像であるための必要十分条件となる。
証明 †
「
」 を
、「
が1対1写像」を
として、
■必要であること (
) の対偶 (
) を証明:
線形写像なら必ず
だから、
ということはつまり
ただし
となる
が存在するということになる。
にもかかわらず
より、
複数の元が
に移る。すなわち1対1写像ではない。
■十分であること (
) の対偶 (
) を証明:
かつ
ならば
より
かつ
となって、
次元定理 †
上記をまとめると下図のようになる。
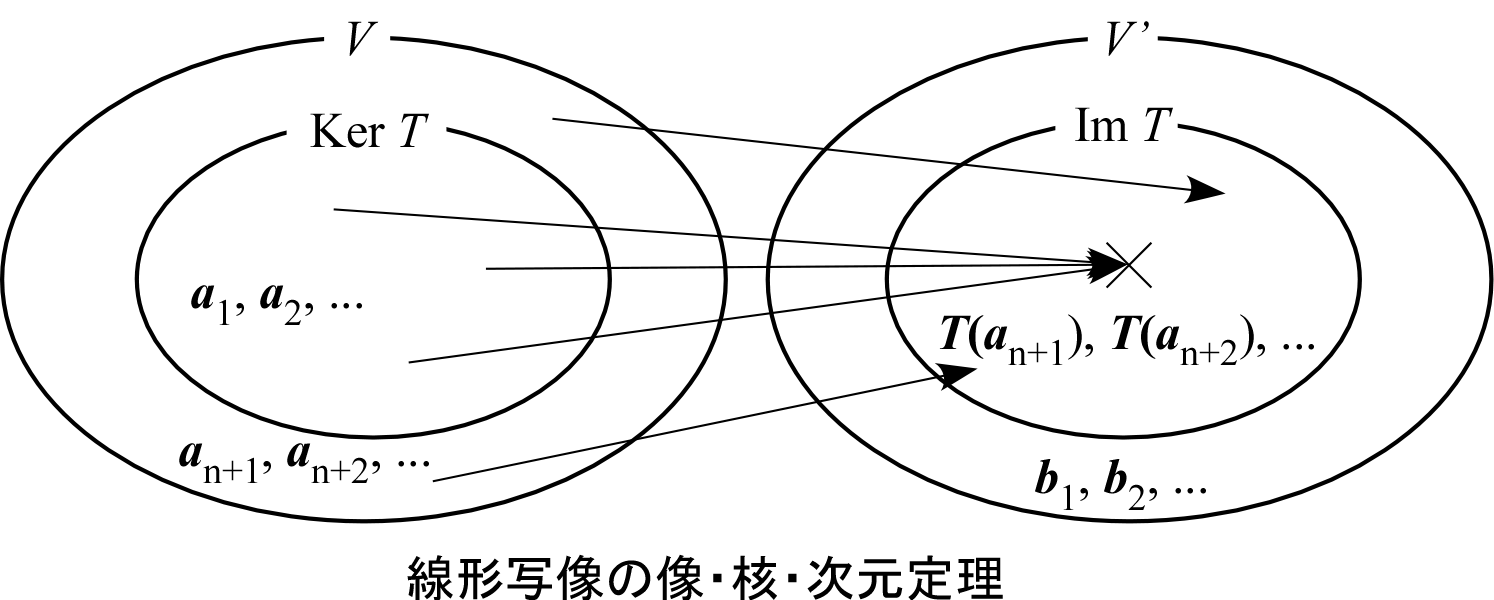
-
は
の、
は
の、部分空間である
-
に含まれる元は
に移る
-
に含まれる元は
に移る
線形写像の次元定理とは、次の関係のことである。
(イメージ的には上の 3. そのまま)
略証明:
の基底を
として(つまり、
) 、
これにいくつかベクトルを加えた
が
の基底となるようにできる。(本当は証明が必要)
は
によってすべて
に移る一方、
は
に移り、
は
の基底を為す。
すなわち、
退化次数 †
もともと
の次元を持つ線形空間が、
で移されることにより
だけ次元が減ってしまうため、
を退化次数と呼ぶ。
練習 †
行列による線形写像の階数 †
上で見たように、
の時、
(右辺は
が張る空間)であるから、
は
の列ベクトルが張る空間の次元となる。
そしてこれは次に見るとおり
に等しい。
すなわち
略証明 †
まず任意の行列
は、ある正則行列
により階段化可能であり、
その「段数」が
であった。
階段形から、
の列ベクトルが張る空間の次元が
に等しいことはすぐに分かる。
すなわち
に対して
さらに、
は、
と
との間の同型写像を定義する。
(
を掛けるのが逆写像)
同型な空間の次元は等しいため、
すなわち、
練習問題 †
から
への線形写像を
として定義する。
(
)。
として次のものが与えられたとして、以下の問いに答えよ。
(1) 行列
の階数を求めよ
(2)
の核の基底を1組定め、核の次元を答えよ。
(3)
の像の基底を1組定め、像の次元(
の階数)を答えよ。
(4)
で変換すると (3) で求めた基底のベクトルと重なるベクトルをそれぞれ1つずつ求めよ。
(5) (2) で求めた基底ベクトルと、(4) で求めたベクトルとを合わせると元の空間
の基底となることを確認せよ。
解答例と解説 †
(1) †
行列の階数を求めるにはガウスの消去法(掃出し法)を適用して階段行列化した際の非ゼロな行数を数えれば良いのであった。
したがって、
1年生では習っていない場合もあるかもしれないが、実は階数を求めるには行ではなく列方向に掃き出してゼロでない列数を数えてもよい(同じ値になる)ことを証明できる。ここでも念のため等しい値になることを確かめておく。
確かに非ゼロ列は2列になる。これは
が
の列ベクトルに含まれる一次独立なベクトルの本数に等しい。
(2) †
の核は
で変換するとゼロになるベクトルの集合であるから、
つまり
を解けば良い。(1) の途中結果を使いつつ拡大係数行列を変形して、
これは、
を意味するので、掃出しを行えなかった列に相当する
をパラメータ
で置き換えて、
あるいは、
この2つのベクトルは核を張り、しかも1次独立であるため、核の基底となる。
核の次元は基底を構成するベクトルの数であるから、
上記より、以下のように次元定理を理解できる。
(3) †
(1) の後半の結果を利用して、
したがって、
の像はこれら2つのベクトルで張られ、しかもこれらは一次独立であるから、
が像の基底となる。
(4) †
を満たすのは例えば
を満たすのは例えば
(5) †
ここで、
よりこの行列は正則。すなわち
と
は1対1に対応し、
これら4本のベクトルが元の空間
を張ることが分かる。
このように
を
で表すと、
は
となる。
が成り立つことを再度理解せよ。
前の単元 <<<
線形代数II
>>> 次の単元