前の単元 <<<
線形代数II
>>> 次の単元
無限次元の線形空間 †
これまで主に、有限個数のベクトルで張ることのできる、
有限次元の線形空間について学んできた。
線形空間にはこれ以外に、有限個のベクトルで張ることのできない
無限次元の線形空間が存在する。
中でも有用なのが以下で見る関数の線形空間である。
関数の線形空間 = 関数空間 †
閉区間
ただし
で定義された任意の複素関数を要素とする集合
は、
通常の和と定数倍に対して線形空間を為す。
すなわち、
のとき、
を
として、
を
として
定義すれば、
であり、
はこれらの演算に対して閉じている。
以下、数ベクトル空間と対比させながら関数空間について学んでいこう。
ベクトルの値 †
|
のとき、
添字
に対して
をプロットすれば、
「ベクトルのグラフ」を表示できる。
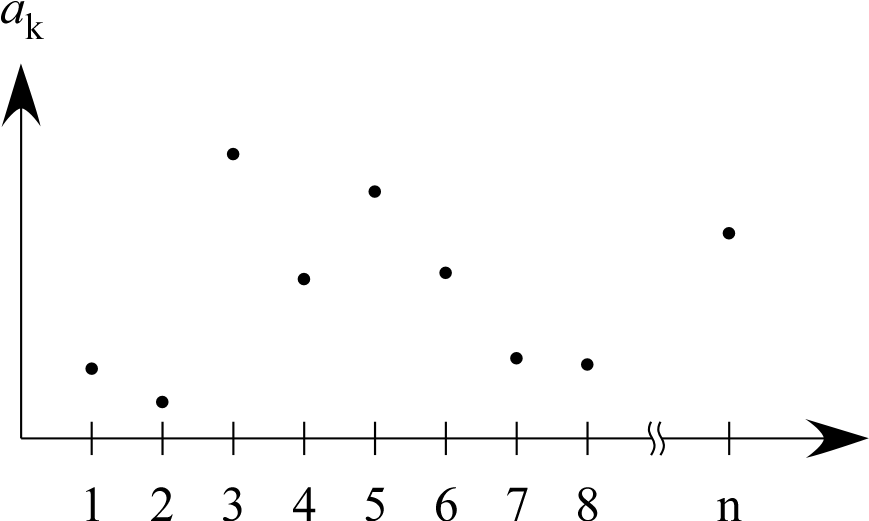
から
への対応関係を1つ決めると、
それが1つのベクトルを決めることに相当する。
|
のとき、
変数
に対して
をプロットすれば、
「関数のグラフ」を表示できる。
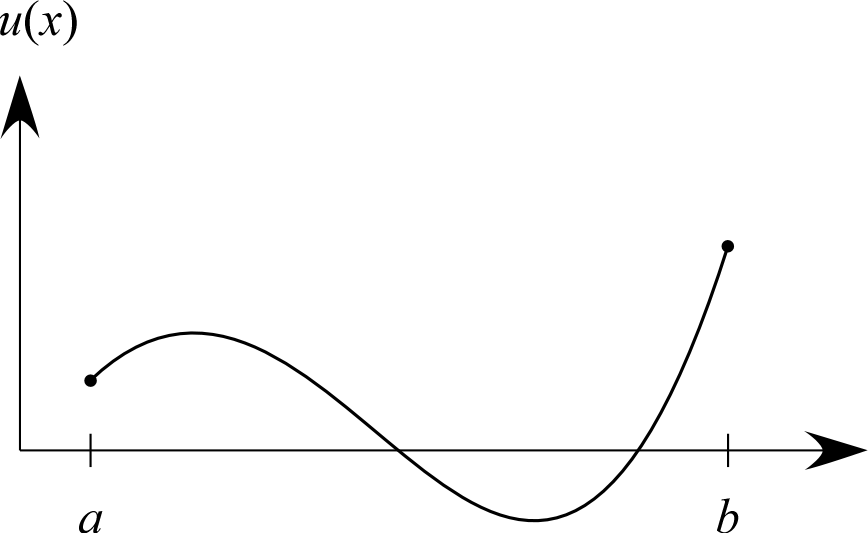
から
への対応関係を1つ決めると、
それが1つの関数を決めることに相当する。
|
このようなグラフを考えれば、
- ベクトルの和はグラフの上下方向への重ね合わせに
- ベクトルの定数倍はグラフの上下方向の引き延ばしに
それぞれ対応する。
ただし、ベクトルや関数の値として複素数を許す場合もあるので、
その場合には3次元的なグラフを考える必要がある。
内積 †
本授業で採用している内積の公理はかけ算の順番が一般的な物と異なるため注意せよ。
関数空間では和ではなく積分で内積を定義できる。
|
標準内積:
少し一般化して、
としても内積の公理を満たす。ただし
はある決まった正の数列で、
個々の成分に付けられた重みに相当する。
|
標準内積:
少し一般化して、
としても良い。ただし、
は「重み関数」と呼ばれる。
|
もっと一般には、標準内積を
として、任意の正定値(固有値が全て正)なエルミート変換
に対して新しい演算
を作れば、この演算は内積の公理を満たす。
正規・直交 †
|
正規性:
直交:
正規直交:
ベクトルの組
に対して
|
正規性:
直交:
正規直交:
関数の組
に対して
|
完全性・成分表示 †
|
あるベクトルの組
が「線形空間
を張る」 とは、
任意の
を次の形に表せること。
|
ある関数系
が集合
で完全であるとは、
任意の関数
を次の形に表せること。
無限次元なので、和の上限は
となる。
実際には
の
までの和を取るわけには行かないため、
この表示は
のときに左辺と右辺との差がゼロに近づくことを表わす。つまり、
例えば、関数系
は、任意の無限回微分可能な関数を
と表せることから、無限回微分可能な関数全体が作る線形空間において完全系をなす。
(
でのテイラー展開 = マクローリン展開)
|
|
正規直交基底
により
と分解するとき、
その
成分を
として求められる。(あるいは
)
すなわち、
数ベクトル空間では内積を行列の積で表して、
が任意の
に対して成り立つから、
である。
|
正規直交関数系
により
と分解するとき、
その
の係数を
として求められる。すなわち、
この式を変形すれば
となり、これが任意の関数
に対して成り立つならば、
である。この式を完全性の条件とする場合もある。
|
与えられた関数をこのように正規直交な完全関数系で展開することを、
「フーリエ式展開」と呼ぶ。
|
正規直交基底
に対するベクトル
の表現を
とすれば、
→ 正規直交基底に対する内積の成分表示 を参照
|
パーセバルの等式:
ある正規直交関数系
が完全であることと、
任意の関数
に対して
を求めた際に
を満たすこととは同値となる。この等式はパーセバルの等式と呼ばれる。
例えば、
が完全であるとき、
は完全でない。
このように関数系が不完全なときは、右辺の項数が不足する。
両方合わせると、任意の正規直交関数系
に対して
が成り立つ。これをベッセルの不等式と呼ぶ。
|
ここまでの話は、積分や無限級数の和が収束することが条件となっていて、
そういった性質の良い関数空間にはバナッハ空間とか、ヒルベルト空間などの名前が付いている。
正規直交な完全関数系の例 †
授業で扱う範囲においては、
ルジャンドル(Legendre)多項式 は主に量子力学で、
実・複素フーリエ級数は 波動・電気回路・信号処理などの他にも幅広い分野で、
活用されることになる。
ルジャンドル(Legendre)多項式 †
ルジャンドル多項式は、内積の積分範囲を
とし、重み関数を
ととり、
をシュミットの直交化法を用いて直交化して得られる関数系である。
(厳密には係数分だけ異なる)
と同様に、無限回微分可能な関数を要素とする関数空間に於いて完全系をなす。
|
1)
|
2)
|
3)
|
これを続けると、一般に
の形が得られる。式中で
として表わした部分がルジャンドル多項式と呼ばれる。
具体的な形は、
などとなる。
実フーリエ級数展開 †
区間
を定義域とする実関数空間に、
重み関数 = 1 として内積を導入するとき、
は正規直交基底を為す。→ 正規直交性を確かめよ
と展開するとき、各係数は、
として与えられる。
微分不可能な点を持っているような関数を含む、
ルジャンドル多項式で表せる空間よりもさらに広い空間で完全系となる。
複素フーリエ級数展開 †
区間
を定義域とする複素関数空間に、
重み関数 = 1 として内積を導入するとき、
は正規直交基底を為す。→ 正規直交性を確かめよ
と展開するとき、各係数は、
として与えられる。
微分不可能な点を持っているような関数を含む、
ルジャンドル多項式で表せる空間よりもさらに広い空間で完全系となる。
演習1 †
区間
を定義域とするたちの良い実関数空間に、内積を
として導入すると、関数系
は、正規直交完全系となる。
を上記関数系で展開した際の展開係数を求めよ。
(実フーリエ展開せよ、ということ)
解答 †
この問題は、
と展開するときの
を求めろ、ということである。
正規直交系であるから、係数はそれぞれ、
として求められる。
まず、
は偶関数なので、
一方、
に対して、
となる。
すなわち、
グラフを書いてみると、項数を増やすに従って徐々に
に漸近していく様子が分かる。
前の単元 <<<
線形代数II
>>> 次の単元

