相互作用のない複数粒子のスレーター行列
概要 †
多粒子波動関数をそのまま扱うことは数学的にも、数値計算的にも、人間の理解としても大きな困難を伴うため、 ここでは、1粒子波動関数を組み合わせて多粒子波動関数を構成する基本的な考え方を学び、 その知識をもとに多粒子波動関数の性質について理解していくことにする。
目次 †
相互作用のない2つの粒子 †
例として、遠く離れた2つの水素原子を考える。
このときそれぞれは互いに独立した系とみなせるから、2つの原子核の位置を $\bm R_1,\bm R_2$ として、
原子核 1 の周りの電子の存在確率は $|\varphi_0(\bm r-\bm R_1)|^2$ と
原子核 2 の周りの電子の存在確率は $|\varphi_0(\bm r-\bm R_2)|^2$ と
ほぼ等しいはずである。
ただし、孤立水素原子の基底状態の、時間によらない波動関数を $\varphi_0(\bm r)$、 そのエネルギーを $\varepsilon_0$ とした。
そこで、
$$\varphi_1(\bm r)=\varphi_0(\bm r-\bm R_1)$$ $$\varphi_2(\bm r)=\varphi_0(\bm r-\bm R_2)$$
と置き、系全体の波動関数を
$$\mathit\Phi(\bm r_1,\bm r_2)=\varphi_1(\bm r_1)\varphi_2(\bm r_2)$$
としてみると、これは電子1が $\bm R_1$ 付近に、電子2が $\bm R_2$ 付近に局在する2粒子系波動関数となる。事実、$\bm r_1\sim\bm R_1$ かつ $\bm r_2\sim\bm R_2$ でない限り $\mathit\Phi$ は実質的にゼロとなるから、$\mathit\Phi/|\bm r_1-\bm R_2|$ や $\mathit\Phi/|\bm r_2-\bm R_1|$、$\mathit\Phi/|\bm r_1-\bm r_2|$ などの項は無視できて、
$$ \begin{aligned} \hat H\mathit\Phi(\bm r_1,\bm r_2)&= \underbrace{\left[-\frac{1}{2m}\bm \nabla_{\bm r_1}^2-\frac{1}{4\pi\epsilon_0}\frac{e^2}{|\bm r_1-\bm R_1|}\right]} _{\displaystyle\hat H_1}\mathit\Phi(\bm r_1,\bm r_2) {}+\underbrace{\left[-\frac{1}{2m}\bm \nabla_{\bm r_2}^2-\frac{1}{4\pi\epsilon_0}\frac{e^2}{|\bm r_2-\bm R_2|}\right]} _{\displaystyle\hat H_2}\mathit\Phi(\bm r_1,\bm r_2) {}+\,\text{(無視)}\\ &\sim\hat H_1\varphi_1(\bm r_1)\varphi_2(\bm r_2)+\hat H_2\varphi_1(\bm r_1)\varphi_2(\bm r_2)\\[1mm] &=\big[\hat H_1\varphi_1(\bm r_1)\big]\varphi_2(\bm r_2) {} +\varphi_1(\bm r_1)\big[\hat H_2\varphi_2(\bm r_2)\big]\\[1mm] &=\varepsilon_0\varphi_1(\bm r_1)\varphi_2(\bm r_2)+\varepsilon_0\varphi_1(\bm r_1)\varphi_2(\bm r_2)\\[1mm] &=2\varepsilon_0\mathit\Phi(\bm r_1,\bm r_2) \end{aligned} $$
のように、近似的にエネルギー固有値 $E=2\varepsilon_0$ の固有関数となっている。
このように、「独立な1体シュレーディンガー方程式の解を単に掛け合わせた形」は「ハートリー積」 と呼ばれ、相互作用のない粒子に対する多体のシュレーディンガー方程式を満たす解を作る簡便な方法となる。
また、$\hat H$ は粒子の入れ替えに対して対称だから、$\bm r_1$ と $\bm r_2$ とを入れ替えた、
$$\mathit\Phi(\bm r_2,\bm r_1)=\varphi_1(\bm r_2)\varphi_2(\bm r_1)$$
このことは、$\varphi_1(\bm r_1)\varphi_2(\bm r_2)$ と $\varphi_1(\bm r_2)\varphi_2(\bm r_1)$ とが縮退した2つの独立した解を与える、ということにはならないところが重要である。 これらは2つの粒子の入れ替えにより互いに入れ替わるから、 同種粒子の不可弁別性によりそもそも区別されるべきではない、同一の状態であると言える。
それにもかかわらず $\varphi_1(\bm r_1)\varphi_2(\bm r_2)$ と $\varphi_1(\bm r_2)\varphi_2(\bm r_1)$ とは数学的に見れば明らかに異なる関数であり、 さらにどちらもがハミルトニアンの固有関数であるから、ハミルトニアンの線形性により任意の $A,B$ に対して
$$\mathit\Phi(\bm r_2,\bm r_1)=A\varphi_1(\bm r_1)\varphi_2(\bm r_2)+B\varphi_1(\bm r_1)\varphi_2(\bm r_2)$$
は $E=2\varepsilon_0$ に対応するシュレーディンガー方程式の解となる。
以上を、多粒子系のシュレーディンガー方程式では「対称性を指定しない限り解が1つに定まらない」 という事実を示す例として理解せよ。「$\varphi_1(\bm r)$ と $\varphi_2(\bm r)$ により表される 2つの1粒子状態がそれぞれ1つずつの電子に寄り占有された状態」を表す波動方程式に含まれる パラメータ $A$ と $B$ とは、電子がフェルミ粒子であることから、 その入れ替えに対して波動関数が反対称でなければならないという制約によって決められることを以下に見る。
対称性を満たす解 †
1つのハートリー積により作られた波動関数はボーズ粒子、フェルミ粒子に要求される対称性、反対称性 $\Phi(\bm r_2,\bm r_1)=\pm\Phi(\bm r_1,\bm r_2)$ を満たさない。「電子 1 が $\bm R_1$ 付近に、電子 2 が $\bm R_2$ 付近に存在する」というのは明らかに2つの電子を区別しており、そのような波動関数は不可弁別性を満たさないためだ。
一方、上記で見たような
「電子 1 が $\bm R_1$ 付近に、電子 2 が $\bm R_2$ 付近に存在する」解と
「電子 2 が $\bm R_1$ 付近に、電子 1 が $\bm R_2$ 付近に存在する」解と
を混ぜ合わせた解の係数をうまく選ぶことにより、フェルミオンやボゾンに要求される対称性を満たす解を構成可能である。(さしあたり以下では2つの電子が同じスピンを持っているとする)
つまり、フェルミオンなら
$$\mathit\Phi(\bm r_1,\bm r_2)=A\big\{\varphi_1(\bm r_1)\varphi_2(\bm r_2)-\varphi_1(\bm r_2)\varphi_2(\bm r_1)\big\}$$
ボゾンなら、
$$\mathit\Phi(\bm r_1,\bm r_2)=A\big\{\varphi_1(\bm r_1)\varphi_2(\bm r_2)+\varphi_1(\bm r_2)\varphi_2(\bm r_1)\big\}$$
と取ることで、必要な対称性を満たせる。
どちらも、$\varphi_1(\bm r)$ と $\varphi_2(\bm r)$ が正規直交なら、$\varphi_1(\bm r_1)\varphi_2(\bm r_2)$ と $\varphi_1(\bm r_2)\varphi_2(\bm r_1)$ も正規直交であるから、$|A|=1/\sqrt 2$ とすれば規格化された解となる。(上の例において $\varphi_1(\bm r)\ne 0$ である範囲で常に $\varphi_2(\bm r)= 0$ と見なせるなら近似的に直交する)
これらはどちらも $\varphi_1$ と $\varphi_2$ の2つの1粒子状態が2つの粒子により占有された状態を表す。
シュレーディンガー方程式に加えて対称性を指定することで、位相を除いてシュレーディンガー方程式の解が一意に定まったことを確認せよ。
以上は相互作用のない2つの1粒子波動関数から、フェルミ粒子やボーズ粒子の2粒子波動関数を作る標準的な手順である。
(2つの電子が異なるスピンを持つ可能性を考慮すると、原子1側に $\varphi_{1\uparrow},\varphi_{1\downarrow}$ 原子2側に $\varphi_{2\uparrow},\varphi_{2\downarrow}$ を取れるから、下記のスレーター行列の略記法を用いて $\det\big(\ \varphi_{1\uparrow}\ \ \varphi_{2\uparrow}\ \big)/\sqrt{2}$、 $\det\big(\ \varphi_{1\uparrow}\ \ \varphi_{2\downarrow}\ \big)/\sqrt{2}$、 $\det\big(\ \varphi_{1\downarrow}\ \ \varphi_{2\uparrow}\ \big)/\sqrt{2}$、 $\det\big(\ \varphi_{1\downarrow}\ \ \varphi_{2\downarrow}\ \big)/\sqrt{2}$ の4通りを作れる)
スレーター行列 †
フェルミオンの場合 = 行列式 †
上でフェルミオンの波動関数が以下の性質を持たなければならないことを学んだ。
- 座標を入れ替えると符号が反転する
- 同じ座標が2つ以上あるとゼロになる
これは行列式の以下の性質とよく似ている。
- 2つの列を入れ替えると符号が反転する
- 同じ列が2つ以上あるとゼロになる
実際、上で見た反対称な2電子の波動関数は($\varphi_j$ が正規直交系になっていれば)
$$ \begin{aligned} \Phi(\bm r_1,\bm r_2) &=\frac{1}{\sqrt 2}\Big[\varphi_1(\bm r_1)\varphi_2(\bm r_2)-\varphi_1(\bm r_2)\varphi_2(\bm r_1)\Big]\\ &=\frac{1}{\sqrt 2}\det\begin{pmatrix} \varphi_1(\bm r_1) & \varphi_1(\bm r_2) \\ \varphi_2(\bm r_1) & \varphi_2(\bm r_2) \\ \end{pmatrix} \end{aligned} $$
のように2×2の行列式の形に表せる。
一般の多粒子系においても、
$$ \Phi(\bm r_1,\bm r_2,\dots,\bm r_n) =\frac{1}{\sqrt{n!}}\det\begin{pmatrix} \varphi_1(\bm r_1) & \varphi_1(\bm r_2) & \dots & \varphi_1(\bm r_n) \\ \varphi_2(\bm r_1) & \varphi_2(\bm r_2) & & \vdots \\ \vdots & & \ddots & \vdots \\ \varphi_n(\bm r_1) & \dots & \dots & \varphi_n(\bm r_n) \\ \end{pmatrix} $$
とすることで、反対称性を満たす $n$ 個の粒子の波動関数を $n$ 個の1粒子の波動関数から作れる。
この $n$ 粒子波動関数は、$\varphi_1\cdots\varphi_n$ の $n$ 個の状態のそれぞれが、$n$ 個の粒子のうちの特定されない 1 つずつの粒子で占められた状態を表す。
上式の右辺に現れる行列はスレーター行列と呼ばれ、教科書ではその係数と行列式を合わせた省略形として次の記法を用いている。
$$ \Phi(\bm r_1,\bm r_2,\dots,\bm r_n) =|\,\varphi_1, \varphi_2, \dots, \varphi_n\,| $$
ただ、この書き方はわかりにくいので、以下ではこれを
$$ \Phi(\bm r_1,\bm r_2,\dots,\bm r_n) =\frac{1}{\sqrt{n!}}\det\big(\,\varphi_1, \varphi_2, \dots, \varphi_n\,\big) $$
と書くことにする。
行列式の定義 により、これは下記のようにも書ける。
$$ \Phi(\bm r_1,\bm r_2,\dots,\bm r_n) =\frac{1}{\sqrt{n!}}\sum_{(p_1\ p_2\ \cdots\ p_n)}\varepsilon(p_1\ p_2\ \cdots\ p_n) \varphi_1(\bm r_{p_1})\varphi_2(\bm r_{p_2})\dots\varphi_n(\bm r_{p_n}) $$
右辺には $n!$ 個の項が現れる。 それぞれの項は、$n$ 個の粒子をそれぞれどの1粒子状態に割り当てるか、 の割り当て方の1つ1つに対応し、その割り当て方は $n$ 個の1粒子状態に $n$ 個の粒子を割り当てる数として、${}_nP_n=n!$ 通り存在する。 それらに適切な符号を付け、均等に加えたのがスレーター行列式である。 $\set{\varphi_k}$ が正規直交系であれば、$n!$ 個の項も正規直交系をなすため 頭の $1/\sqrt{n!}$ により正規化がなされる。
※本来は1粒子波動関数は空間座標とスピン座標の関数であることに注意せよ
パウリの排他律2 †
スレーター行列式を作る $n$ 個の1粒子波動関数のうち、 $\varphi_j$ と $\varphi_k$ とが同一であるとすると、
$$ \begin{aligned} \Phi(\bm r_1,\bm r_2,\dots,\bm r_n) &=\frac{1}{\sqrt{n!}}\left|\begin{matrix} \varphi_1(\bm r_1) & \dots & \varphi_1(\bm r_n) \\ \vdots&&\vdots\\ \varphi_j(\bm r_1) & \dots & \varphi_j(\bm r_n) \\ \vdots&&\vdots\\ \varphi_k(\bm r_1) & \dots & \varphi_k(\bm r_n) \\ \vdots&&\vdots\\ \varphi_n(\bm r_1) & \dots & \varphi_n(\bm r_n) \\ \end{matrix}\right| \begin{array}{l} \\ \\ \leftarrow \text{同一の行になる}\\ \\ \leftarrow \text{同一の行になる}\\ \\ \\ \end{array}\\ &=0 \end{aligned} $$
行列式中にまったく同じ行が2つ現れるから、 行列式の値はゼロになる。
すなわち、2つ以上のフェルミ粒子が同じ1粒子量子状態を占めることはできない。
こちらが通常の意味でのパウリの排他律である。
正確には粒子の座標は空間座標とスピン座標の両方で指定されるため、 波動関数の空間座標部分が同一でも、スピン座標成分が異なれば同一とは見なされない。
(参考)ボゾンの場合 = パーマネント †
ボゾンの場合には各項の符号を与える $\varepsilon(p_1\ p_2\ \cdots\ p_n)$ の部分を $+1$ に置き換えれば、粒子の入れ替えで値の変わらない形が得られる。 行列式(デターミナント)に現れる符号をすべて $+1$ に置き換えた形は パーマネントと呼ばれるため、以下では次のように表す。
$$ \begin{aligned} \Phi(\bm r_1,\bm r_2,\dots,\bm r_n) &=A\sum_{(p_1\ p_2\ \cdots\ p_n)}(+1)\cdot \varphi_1(\bm r_{p_1})\varphi_2(\bm r_{p_2})\dots\varphi_n(\bm r_{p_n})\\ &=A\,\mathrm{perm}\,\big(\,\varphi_1, \varphi_2, \dots, \varphi_n\,\big) \end{aligned} $$
$A$ は規格化定数であるが、フェルミオンの場合と異なりスレーター行列内に同じ波動関数が 複数現れる可能性があるため、$A=1/\sqrt{n!}$ とはならない。
というのも、$k$ 番目の1粒子状態に $n_k$ 個の粒子が入るとすれば、 それらに与える座標を入れ替えてもまったく同じ形の関数になる。 パーマネントの中にそのような項は $\prod_k n_k!$ 個あるから、 それらをまとめて書けば、
$$ \begin{aligned} \Phi(\bm r_1,\bm r_2,\dots,\bm r_n) &=A\sum_{代表の(p_1\ p_2\ \cdots\ p_n)} \Big(\prod_k n_k!\Big)\cdot \varphi_1(\bm r_{p_1})\varphi_2(\bm r_{p_2})\dots\varphi_n(\bm r_{p_n})\\ &=A\Big(\prod_k n_k!\Big)\sum_{代表の(p_1\ p_2\ \cdots\ p_n)} \varphi_1(\bm r_{p_1})\varphi_2(\bm r_{p_2})\dots\varphi_n(\bm r_{p_n}) \end{aligned} $$
$\sum$ 内の項は正規直交であり、項数は $\frac{n!}{\prod_k n_k!}$ であるから、
$$ \int|\Phi|^2\,d\bm r_1d\bm r_2\cdots d\bm r_n =A^2\Big(\prod_k n_k!\Big)^{\cancel 2}\frac{n!}{\cancel{\prod_k n_k!}} =A^2 n!\prod_k n_k!=1 $$
より、正規化した形は次のようになる。
$$ \Phi(\bm r_1,\bm r_2,\dots,\bm r_n) =\frac{1}{\sqrt{n!\prod_k n_k!}}\,\mathrm{perm}\,\big(\,\varphi_1, \varphi_2, \dots, \varphi_n\,\big) $$
(発展)スレーター行列式のユニタリ変換 †
関数系 $\{\chi_i\}$ が正規直交関数系 $\{\varphi_i\}$ と同じ空間を張る正規直交関数系であるとする。すなわち、あるユニタリ行列 $U=(u_{ij})$ に対して
$$ \Big( \begin{matrix} \chi_1(\bm r)& \chi_2(\bm r)& \dots& \chi_n(\bm r) \end{matrix}\Big)= \Big(\begin{matrix} \varphi_1(\bm r)& \varphi_2(\bm r)& \dots& \varphi_n(\bm r) \end{matrix}\Big) \begin{pmatrix} u_{11}&u_{12}&\dots&u_{1n}\\ u_{21}&\ddots&&\vdots\\ \vdots&&\ddots&\vdots\\ u_{n1}&\dots&\dots&u_{nn}\\ \end{pmatrix} $$
の関係があるとするということである。
このとき、$\det\big(\,\chi_1,\chi_2,\dots,\chi_n\,\big)$ と $\det\big(\,\varphi_1,\varphi_2,\dots,\varphi_n\,\big)$ とは絶対値が1となる係数(複素位相)を除いて一致する。 なぜなら、
$$ \begin{aligned} \begin{vmatrix} \chi_1(\bm r_1)&\chi_2(\bm r_1)&\dots&\chi_n(\bm r_1)\\ \chi_1(\bm r_2)&\ddots&&\vdots\\ \vdots&&\ddots&\vdots\\ \chi_1(\bm r_n)&\dots&\dots&\chi_n(\bm r_n)\\ \end{vmatrix}&=\left| \ \begin{pmatrix} \varphi_1(\bm r_1)&\varphi_2(\bm r_1)&\dots&\varphi_n(\bm r_1)\\ \varphi_1(\bm r_2)&\ddots&&\vdots\\ \vdots&&\ddots&\vdots\\ \varphi_1(\bm r_n)&\dots&\dots&\varphi_n(\bm r_n)\\ \end{pmatrix} \begin{pmatrix} u_{11}&u_{21}&\dots&u_{n1}\\ u_{12}&\ddots&&\vdots\\ \vdots&&\ddots&\vdots\\ u_{1n}&\dots&\dots&u_{nn}\\ \end{pmatrix}\ \right|\\ &=\begin{vmatrix} \varphi_1(\bm r_1)&\varphi_2(\bm r_1)&\dots&\varphi_n(\bm r_1)\\ \varphi_1(\bm r_2)&\ddots&&\vdots\\ \vdots&&\ddots&\vdots\\ \varphi_1(\bm r_n)&\dots&\dots&\varphi_n(\bm r_n)\\ \end{vmatrix} \left|U\right| \end{aligned} $$
であり、$|U|$ はユニタリ行列の行列式なので絶対値は1となる。
これは、$\varphi_1,\dots,\varphi_n$ に1つずつ粒子が入っている多粒子状態 $\Phi$ と、 $\chi_1,\dots,\chi_n$ に1つずつ粒子が入っている多粒子状態 $\Phi'$ とは、物理的に等しいということを示している。 ($3n$ 次元空間における確率密度分布が等しくなる)
$$ |\Phi|^2 =\Big|(1/\sqrt{n!})\det\begin{pmatrix}\varphi_1&\varphi_2&\dots&\varphi_n\end{pmatrix}\Big|^2 =\Big|(1/\sqrt{n!})\det\begin{pmatrix}\chi_1&\chi_2&\dots&\chi_n\end{pmatrix}\Big|^2 =|\Phi'|^2 $$
これは、たとえば3次元調和振動子において
$x,y,z$ 座標で解いた $N=1$ の3つの1粒子状態 $(n_x,n_y,n_z)=(1,0,0),(0,1,0),(0,0,1)$ のそれぞれを粒子が1つずつ占める状態と、
$r,\theta,\phi$ 座標で解いた $N=1$ の3つの1粒子状態 $(n,l,m)=(0,1,-1),(0,1,0),(0,1,+1)$ のそれぞれを粒子が1つずつ占める状態と、
は等しいことを示している(この授業では詳しくやらないが、ハートリー・フォック法などでこのことが生きてくる)。
対称性・反対称性を満たす波動関数 †
対称性・反対称性を満たす波動関数は、スレーター行列から作られる上記の形以外にも様々なものが考えられる。というのも、対称性・反対称性を満たす波動関数の線形結合はやはり同じ対称性を持つためだ(対称・反対称な波動関数の集合は線形空間となる=対称変換 $\hat P_{ij}$ の固有空間=フォック空間と呼ばれる)。
たとえば、「単一のスレーター行列式から作った多体波動関数」を 複数重ね合わせたものはやはり反対称な波動関数となる。 1粒子の正規直交完全系から $n$ 個の異なる関数を取り出して作ることのできるすべてのスレーター行列を集めれば、$n$ 粒子系における「完全系」ができあがる。
スレーター行列を使う方法の他にも、任意の、 特別な対称性を持たない多体波動関数 $\Phi(\bm r_1,\bm r_2,\dots,\bm r_n)$ から、
$$ \Phi_\mathrm{asym}(\bm r_1,\bm r_2,\dots,\bm r_n)= A\sum_{(p_1\ p_2\ \dots\ p_n)} \varepsilon(p_1\ p_2\ \dots\ p_n) \Phi(\bm r_{p_1},\bm r_{p_2},\dots,\bm r_{p_n}) $$
として、反対称な多体波動関数を得ることが可能である。対称なものを作りたければ
$$ \Phi_\mathrm{sym}(\bm r_1,\bm r_2,\dots,\bm r_n)= A\sum_{(p_1\ p_2\ \dots\ p_n)} \Phi(\bm r_{p_1},\bm r_{p_2},\dots,\bm r_{p_n}) $$
とすればよい。例えば3粒子であれば $\Phi(\bm r_1,\bm r_2,\bm r_3)$ から、
$$ \Phi(\bm r_1,\bm r_2,\bm r_3)+\Phi(\bm r_2,\bm r_3,\bm r_1)+\Phi(\bm r_3,\bm r_1,\bm r_2) \pm\Phi(\bm r_1,\bm r_3,\bm r_2)\pm\Phi(\bm r_3,\bm r_2,\bm r_1)\pm\Phi(\bm r_2,\bm r_1,\bm r_3) $$
を作ると、複合で $+$ を取れば対称な、$-$ を取れば反対称な関数となるのである。
元の $\Phi(\bm r_1,\bm r_2,\dots,\bm r_n)$ が多体ハミルトニアンの固有関数であるなら、 $\Phi_\mathrm{asym}$ や $\Phi_\mathrm{sym}$ も同じエネルギーに対する固有関数となる事に注意せよ。ここから、「多体ハミルトニアンの固有関数である」という条件では波動関数が一意に決まらないことを再々確認せよ。
交換相互作用 †
2粒子系波動関数をハートリー積で作った場合には、 確率密度の $\bm r_1$ に対する依存性は、$\bm r_2$ によらず一定であり、 両者の間に相関はない。
$$|\Phi(\bm r_1,\bm r_2)|^2=|\varphi_1(\bm r_1)|^2\,|\varphi_2(\bm r_2)|^2$$
複合確率が個々の確率の積になるのは、両者に相関がなく独立であることを示している。
一方、2粒子系波動関数をスレーター行列式で書いた場合、
$$ \begin{aligned} \Big|\Phi(\bm r_1,\bm r_2)\Big|^2 &=A^*\Big(\varphi_1(\bm r_1)\varphi_2(\bm r_2)-\varphi_1(\bm r_2)\varphi_2(\bm r_1)\Big)^*A\Big(\varphi_1(\bm r_1)\varphi_2(\bm r_2)-\varphi_1(\bm r_2)\varphi_2(\bm r_1)\Big)\\ &=A^2\Big[ \big|\varphi_1(\bm r_1)\varphi_2(\bm r_2)\big|^2+\big|\varphi_1(\bm r_2)\varphi_2(\bm r_1)\big|^2 {}-\varphi_1(\bm r_1)\varphi_2(\bm r_2)\varphi_1^*(\bm r_2)\varphi_2^*(\bm r_1) {}-\varphi_1^*(\bm r_1)\varphi_2^*(\bm r_2)\varphi_1(\bm r_2)\varphi_2(\bm r_1) \Big]\\ &=A^2\Big[ \big|\varphi_1(\bm r_1)\varphi_2(\bm r_2)\big|^2+\big|\varphi_1(\bm r_2)\varphi_2(\bm r_1)\big|^2 {}-2\,\mathrm{Re}\Big\{\varphi_1(\bm r_1)\varphi_2(\bm r_2)\varphi_1^*(\bm r_2)\varphi_2^*(\bm r_1)\Big\} \Big]\\ \end{aligned} $$
1粒子の時間によらない波動関数は常に実数に取れることを利用すると、
$$ \Big|\Phi(\bm r_1,\bm r_2)\Big|^2 =A^2\Big[ \big|\varphi_1(\bm r_1)\big|^2\big|\varphi_2(\bm r_2)\big|^2+\big|\varphi_1(\bm r_2)\big|^2\big|\varphi_2(\bm r_1)\big|^2 {}-2\varphi_1(\bm r_1)\varphi_2(\bm r_1)\varphi_1(\bm r_2)\varphi_2(\bm r_2) \Big] $$
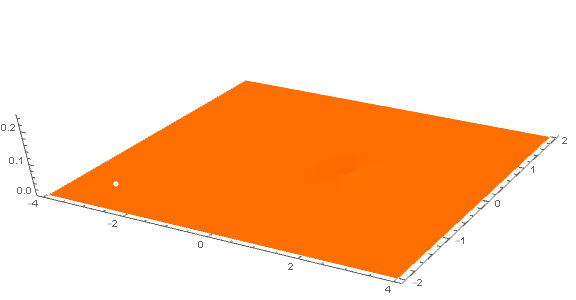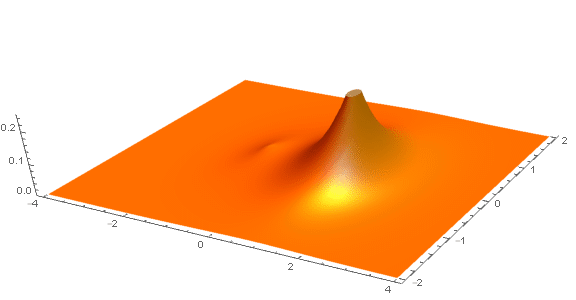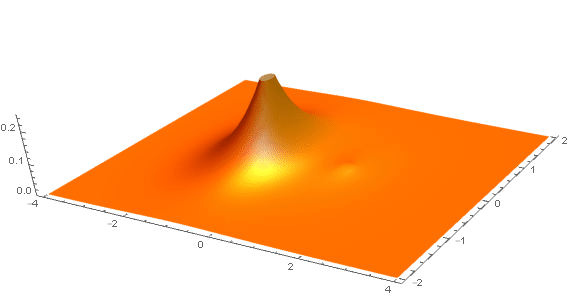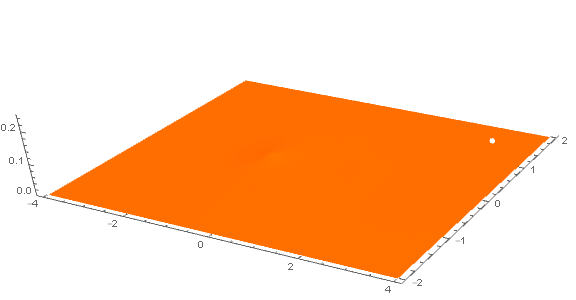
となって、$\bm r_2$ の値によって $\bm r_1$ の確率分布は大きく変化する(相関を持つ)。
下図は、$\bm r_2$ の位置を変えつつ $|\Phi(\bm r_1,\bm r_2)|^2$ の分布をプロットした。確率密度が $\bm r_2$ の位置を避けるように移動する様子が分かる。
この2つの粒子が互いに避けるように分布する相互作用はクーロン反発から生じるものではないという点は重要である。ここでは2つの粒子間に働くポテンシャルは完全に無視していたのを思い出そう。
この「見かけ上の斥力相互作用」は、波動関数を $\bm r_1$ と $\bm r_2$ の入れ替えに対して反対称にしたことにより生じたものであり、「交換相互作用」と呼ばれる。繰り返しになるが、交換相互作用はハミルトニアンに含まれるポテンシャルとはまったく関係のないものであることに注意せよ。事実、単純なハートリー積として構築した波動関数も、2つのハートリー積により反対称化した波動関数も、どちらも同じポテンシャルに対応する同じハミルトニアンの固有関数であり、その固有値(エネルギー)も等しいのであった。
2つの粒子が独立ではなく、2粒子間にポテンシャルがある場合には、交換相互作用はこの2粒子間ポテンシャルを通じてエネルギーに影響を与える。例えば電子の場合、2粒子間に斥力ポテンシャルが存在する。波動関数が反対称化されることにより、反対称化する前に比べて2粒子が「より離れて」存在するようになると、その分だけ斥力ポテンシャルが低下し、エネルギーが低下するのである。この点についてはハートリー・フォック法のところで再度触れる。
LANG:mathematica
Table[Table[
Show[
Plot3D[
Module[{phi, r1, r2, R1, R2},
r1 = {x, y};
r2 = {x2, y2};
R1 = {-1, 0};
R2 = {+1, 0};
phi[rr_] := Exp[-Sqrt[rr[[1]]^2 + rr[[2]]^2]];
phi[r1 - R1]^2 phi[r2 - R2]^2 +
phi[r2 - R1]^2 phi[r1 - R2]^2 -
2 phi[r1 - R1] phi[r2 - R1] phi[r1 - R2] phi[r2 - R2]
], {x, -4, 4}, {y, -2, 2}, PlotPoints -> 51,
MaxRecursion -> 5,
AspectRatio -> 1/2, PlotRange -> {Full, Full, {0, 0.25}},
Mesh -> None, ClippingStyle -> Opacity[0.5],
BoundaryStyle -> None,
Boxed -> False,
PlotStyle -> Directive[Orange, Specularity[White, 40]]
],
ListPointPlot3D[{{x2, y2, 0.01}},
PlotStyle -> {White, PointSize[0.01]}],
ImageSize -> {576, 300}],
{x2, -3, 3, 0.15}
] // If[OddQ[Round[(y2 + 1.5)/0.3]], Reverse, # &],
{y2, -1.5, 1.5, 0.3}
] // Flatten // Export["sample.gif", #] &;
ボゾンの場合 †
ボゾンの場合にも交換相互作用は働く。
その結果、やはり一方の粒子とは遠い側に確率が大きくなるが、 その影響はフェルミオンの場合よりも小さく、 特に、一方の粒子が存在する近辺でも他方の粒子の存在確率はゼロにならない。
平均的な確率分布 †
2粒子波動関数を粒子2の位置座標で積分することにより、 「平均的な粒子1の確率分布」が得られる。
$$ \begin{aligned} P(\bm r_1) &=\int\Big|\Phi(\bm r_1,\bm r_2)\Big|^2 d\bm r_2\\ &=\int\Big|\Phi(\bm r_2,\bm r_1)\Big|^2 d\bm r_2\ \ \ (粒子2の分布も等しい)\\ &=\frac{1}{2}\Big[ \big|\varphi_1(\bm r_1)\big|^2\underbrace{\int\big|\varphi_2(\bm r_2)\big|^2d\bm r_2}_{=\,1} {}+\big|\varphi_2(\bm r_1)\big|^2\underbrace{\int\big|\varphi_1(\bm r_2)\big|^2d\bm r_2}_{=\,1} \pm 2\varphi_1(\bm r_1)\varphi_2(\bm r_1)\underbrace{\int\varphi_2(\bm r_2)\varphi_1(\bm r_2)d\bm r_2}_{=\,0} \Big]\\ &=\frac{1}{2}\Big[\big|\varphi_1(\bm r_1)\big|^2+\big|\varphi_2(\bm r_1)\big|^2\Big]\\ \end{aligned} $$
複合は上がフェルミ粒子、下がボーズ粒子であるが、 $\varphi_1$ と $\varphi_2$ とが正規直交である場合には両者は同じ解を与え、 粒子の確率分布は単に $|\varphi_1|^2$ と $|\varphi_2|^2$ の平均値となる。
これは「$n$ 個の状態に $n$ 個の粒子が入っている」という状況をよく表している。
(正規直交でない場合には $(\varphi_1,\varphi_2)$ の項が残るため話はここまで単純にはならない)
質問・コメント †
相互作用のない2つの粒子(3回目) †
岡安一壽? ()
武内先生
先生の近似を使い、ハミルトニアンを
H=-(1/2m)ℏ^2∇1^2-(1/2m)ℏ^2∇2^2-(e^2/4πε0❘r1-rA❘)-(e^2/4πε0❘r2-rB❘)
-(e^2/4πε0❘r1-rB❘)-(e^2/4πε0❘r2-rA❘)として考えれば
Φ(r1,r2)={φA(r1)φB(r2)-φA(r2)φB(r1)}/√2はHの固有関数になりますね。Hも対称で美しく自然に受け入れることができます。素晴らしいと思います。
ただ、「粒子の交換⇔関数内での座標の交換」ということには疑問を感じています。
まず、ハミルトニアンが対称でない場合は
Φ(r1,r2)={φA(r1)φB(r2)-φA(r2)φB(r1)}/√2は固有関数になれませんよね。例えば、電子1は磁束密度Baの一様な磁場にあり、電子2は磁束密度Bbの一様な磁場にあり、2つは十分離れているといった場合です。電子スピンと磁場によるエネルギー(e/m)(Ba・msaℏ+Bb・msbℏ)に対応するハミルトニアンは
H=(e/m)(Ba・S1z+Bb・S2z)でハートリー積φa(s1)φb(s2)は正しい固有値を与えます。しかし、スピン座標を入れ替えたφa(s2)φb(s1)の固有値は
(e/m)(Ba・msbℏ+Bb・msbℏ)と変わってしまいます。ですから、スレーター行列式は、この場合、固有関数にはなれません。
関数内での座標の交換で、波動関数の絶対値が変わらない必要もない(観測される物理量は全て固有値ですから)ので、あくまでも仮定ですよね。
- - が・になってしまいました。すみません。 -- 岡安一壽?
- マイナスが・です。本当にすみません。 -- 岡安一壽?
- 表示のおかしかった部分を直させていただきました。
同種の粒子の入れ替えに対してハミルトニアンが常に対称になることは重要な事実です。例えば $n$ 個の電子を含む系で、$j$ 番目の電子と $k$ 番目の電子の位置を入れ替えたとしても、$n$ 個の電子の位置自体はすべて、電子の番号付け以外変化ありません。ですので粒子の入れ替えでエネルギーが変化することはなく、すなわちハミルトニアンは対称なのです。
岡安さんのおっしゃる例で、「電子1は磁束密度Baの一様な磁場にあり、電子2は磁束密度Bbの一様な磁場にあり、2つは十分離れているといった場合です。」というのは電子の位置座標の話と、軌道の分布とがまぜこぜになってしまっているように思います。磁場を感じている電子1の位置に電子1のかわりに電子2がを持ってくれば電子2が同じ磁場を感じるはずです。一方、「軌道1は磁束密度Baの一様な磁場中に局在しており、軌道2は磁束密度Bbの一様な磁場中に局在しており、2つは十分離れている」というのはあり得る話です。その場合、電子1が軌道1を、電子2が軌道2を占有した状態がエネルギー固有状態であれば、逆に電子2が軌道1を、電子1が軌道2を占有しても、同じエネルギー固有値に対する固有状態になるはずです。これはハミルトニアンが粒子の入れ替えに対して対称であるためです。あるいは、それで固有状態ではなくなってしまうなら、それらは同種粒子ではなく、区別可能な粒子であることになります。
そしてこの2つの状態の任意の線形結合はすべて同じエネルギー固有値の固有状態になるところ、実際には対称あるいは反対称な状態のみが実現する、というのがここでの話の流れになっています。 -- 武内(管理人)? - 「粒子の交換⇔関数内での座標の交換」よりも「粒子の交換⇔ポテンシャル内での座標の交換」を意識されると良いかもしれません。 -- 武内(管理人)?
- スピン座標を入れ替える話もするべきでしたね。「粒子1と粒子2とが同種であればポテンシャルは座標の入れ替えに対して対称である」の意味するところは、「粒子1が $\bm r_a$ にいてスピン $s_a$ を持ち、粒子2が $\bm r_b$ にいてスピン $s_b$ を持つ状況」と、「粒子2が $\bm r_a$ にいてスピン $s_a$ を持ち、粒子1が $\bm r_b$ にいてスピン $s_b$ を持つ状況」とで、ポテンシャルが同じ値になるということです。当然このときハミルトニアンも対称になります。 -- 武内(管理人)?
- もう1点。多粒子ハミルトニアンの対称性 で解説したように、同種粒子の入れ替えに対するハミルトニアンの対称性は粒子間に相互作用のあるときも含めて常に成り立つことを指摘しておきます。 -- 武内(管理人)?
(続)相互作用のない2つの粒子 †
岡安一壽? ()
武内 先生
私も
H=-(1/2m)ℏ^2∇1^2-(1/2m)ℏ^2∇2^2-(e^2/4πε0❘r1-rA❘)-(e^2/4πε0❘r2-rB❘)
-(e^2/4πε0❘r1-rB❘)-(e^2/4πε0❘r2-rA❘)とすればうまくいくように思ってけいさんをしたのですが、 φA(r1)φB(r2)にHを作用させる時だけ❘r1-rB❘→∞,❘r2-rA❘→∞とし、
φA(r2)φB(r1)にHを作用させる時だけ❘r1-rA❘→∞,❘r2-rB❘→∞としなくてはなりません。1つの関数の中にある同じr1という2つの変数の片方だけ
❘r1-rA❘→∞という制約があることは認められませんね。
考えてみれば、[H1A+H2B]Φ(r1,r2)=E0Φ(r1,r2)の解をこの場合の系の波動関数と呼ぶことにし、[H1A+H2B]Φ(r2,r1)=E0Φ(r2,r1)も成り立つということが
不可弁別性の神秘的なところなのであって、ハミルトニアンを変えてはいけないんですよね。
- コメントをありがとうございます。おかげさまで説明の足りなかったところがはっきりしてきました。上の議論で無視したのは、「波動関数が値を持つ領域で」ポテンシャルをゼロと見なせる項なのです。例えば、$\varphi_1(\bm r_1)$ は $\bm r_1\sim \bm R_1$ でのみ値を持つため、$\varphi_1(\bm r_1)/|\bm r_1-\bm R_1|$ は $\bm r_1\sim \bm R_1$ で値を持ちますが、$\varphi_1(\bm r_1)/|\bm r_1-\bm R_2|$ は全領域でゼロと見なせます。これが前者を残し、後者を無視してよい理由になります。より分かりやすい書き方ができないか、本文を見直すことにいたします。(不可弁別性はどうも神秘的に語られることが多いのですが、本当はそれほど神秘的な話ではないのではと考えています。現状の私の解説もちょっと神秘性に引きずられてしまっているところが残っているのですが、そうではない説明にできるよう検討中です。) -- 武内(管理人)?
相互作用のない2つの粒子 †
岡安一壽? ()
武内 先生
失礼かと存じますがコメントさせて頂きます。先生の書かれたハミルトニアン H (ハット)は電子1と2の交換で対称ではないと思います。間違えにくいように原子核の座標をRA,RBとします。φA(r)=φ0(r-RA),φB(r)=φ0(r-RB)とします。
H1A=-(1/2m)ℏ^2∇1^2-(e^2/4πε0❘r1-rA❘),
H2B=-(1/2m)ℏ^2∇2^2-(e^2/4πε0❘r2-rB❘)とします。
H=H1A+H2Bは電子1と2の交換をすると、-(e^2/4πε0❘r2-rA❘), -(e^2/4πε0❘r1-rB❘)という、なかった項が
現れてしまうので対称ではありません。
ハートリー積φA(r1)φB(r2)はH1A+H2B の固有関数で
[H1A+H2B]φA(r1)φB(r2)=2E0φA(r1)φB(r2)ですが、φA(r2)φB(r1)は
H1A+H2B の固有関数にはなれません。
(∵ H2BφA(r2)≠E0φA(r2), H1AφB(r1)≠E0φB(r1))
結局、Φ(r1,r2)={φA(r1)φB(r2)-φA(r2)φB(r1)}/√2は
H1A+H2B の固有関数にはなれません。
文字がうまく出せず、見にくくて申し訳ありません。
- 指摘をありがとうございます。おっしゃるとおりですね。どのように直すか検討いたします。 -- 武内(管理人)?
- とんでもございません。あまりに早いお返事に驚きました。 -- 岡安一壽?
- 少し落ち着いて考えてみました。上の議論で意図しているところとしては、$\hat H$ は粒子の入れ替えに対して対称な、近似前のハミルトニアンで、$\Phi=\varphi_1(\bm r_1)\varphi_2(\bm r_2)$ とした場合にはそれが近似的に $\hat H\sim \hat H_1+\hat H_2$ と表せる、というつもりだったのだと思います。粒子を入れ替えて $\Phi=\varphi_1(\bm r_2)\varphi_2(\bm r_1)$ とした場合にはゼロになる項が変わるため $\hat H\sim \hat H_1+\hat H_2$ とはならず、今度は $\hat H'_1=-\frac 1{2m}\bm \nabla_{\bm r_1}^2-\frac1{4\pi\epsilon_0}\frac{e^2}{|\bm r_1-{\color{red}\bm R_2}|}$ 等に対して $\hat H\sim \hat H'_1+\hat H'_2$ となります。そのように考えると、入れ替え後の波動関数に対しても近似的に $\hat H\Phi=2\varepsilon_0\Phi$ が成り立ち、上の解説は大筋として間違ってはいないのですが、今の書き方だとそのあたりが分かりづらいですね。さしあたり脚注を追加しましたが、もう少し何かできないか考え中です。 -- 武内(管理人)?
*1 $\begin{aligned}\hat H\mathit\Phi(\bm r_1,\bm r_2)&=\underbrace{\left[-\frac{1}{2m}\bm \nabla_{\bm r_1}^2-\frac{1}{4\pi\epsilon_0}\frac{e^2}{|\bm r_1-\bm R_2|}\right]}_{\displaystyle\hat H_1'}\mathit\Phi(\bm r_1,\bm r_2)+\underbrace{\left[-\frac{1}{2m}\bm \nabla_{\bm r_2}^2-\frac{1}{4\pi\epsilon_0}\frac{e^2}{|\bm r_2-\bm R_1|}\right]}_{\displaystyle\hat H_2'}\mathit\Phi(\bm r_1,\bm r_2)+\,(その他は無視)\\&\sim\hat H_1'\varphi_1(\bm r_2)\varphi_2(\bm r_1)+\hat H_2'\varphi_1(\bm r_2)\varphi_2(\bm r_1)\\[1mm]&=\varphi_1(\bm r_2)\big[\hat H_1'\varphi_2(\bm r_1)\big]+\big[\hat H_2'\varphi_1(\bm r_2)\big]\varphi_2(\bm r_1)\\[1mm]&=\varepsilon_0\varphi_1(\bm r_2)\varphi_2(\bm r_1)+\varepsilon_0\varphi_1(\bm r_2)\varphi_2(\bm r_1)\\[1mm]&=2\varepsilon_0\mathit\Phi(\bm r_1,\bm r_2)\end{aligned}$
添付ファイル: