電磁気学/Ampère の法則
目次 †
§1-5 Ampère の法則 †
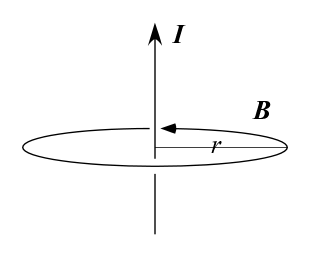
これは電流が磁場を作るという法則である。
$$\begin{aligned}B\propto \frac{I}{r}\end{aligned}$$
すなわち、
$$\begin{aligned}2\pi rB=\mu_0I\end{aligned}$$
と書けることを示した。ただし $\mu_0$ はある定数(実際には真空の透磁率)
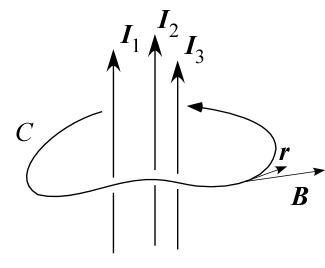
$$\begin{aligned} \oint_C\bm B\cdot d\bm r &=\mu_0 I\\ &=\mu_0 (I_1+I_2+\dots)\\ \end{aligned}$$
と表せることを示した。ただし $I$ は $C$ を貫く電流の総量。 この法則は点電荷の電場から Coulomb の法則を導いたのと同様に、 Oersted の法則と空間の等方性から導くことが可能である。
$\mu_0$ は真空の透磁率と呼ばれる定数であり、その値は次のように定義される。
$$\begin{aligned}\mu_0=4\pi\times 10^{-7}\,\text{N/A}^2\end{aligned}$$
これはたまたま測定値がこのようになったというわけではなく、光速 $c=1/\sqrt{\epsilon_0\mu_0}$ に対して、$\mu_0$ がこの値となるように $\epsilon_0$ の値、ひいては電荷の単位 $C$ を定めたということである。
電流密度 †
ある曲面 $S$ を貫く電流は、電流密度 $\bm i$ を用いて、
$$\begin{aligned}I=\int_S\bm i\cdot\bm n\,dS\end{aligned}$$
と表せるから、$C$ を
$$\begin{aligned}\oint_C\bm B\cdot d\bm r &=\mu_0\int_S\bm i\cdot\bm n\,dS\end{aligned}$$
と表せる。さらにこれを Stokes の定理により変形すれば、Ampère の法則の微分形を
$$\begin{aligned}\frac{1}{\mu_0}\rot\,\bm B=\bm i\end{aligned}$$
として得る。
閉曲線を貫く電流? †
ある閉曲線を貫く磁束が定義できる理由は、$\mathrm{div}\,\bm B=0$ すなわち磁場が常にループを描くことにあった。
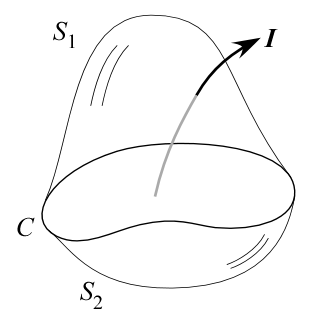
「ある閉曲線を貫く電流」が定義できるためには、これと同様に $\mathrm{div}\,\bm i=0$ が成り立たなければならない。もしどこかで電流が途切れたり、湧き出したりするようなことがあれば、 「閉曲線 $C$ を縁とする曲面」の取り方によって、曲面を貫く電流値が違うことになってしまい、 結果として「閉曲面を貫く電流」が一意に定義されないことになる。
例えば右図では閉曲線 $C$ を縁とする2つの曲面 $S_1,S_2$ に対して、 それらに囲まれる範囲から湧き出した電流 $I$ が $S_1$ は貫くものの、 $S_2$ を貫かない状況を表している。このとき「$C$ を貫く電流」は一意に定義されない。
このことは、上記の Ampère の法則の微分形の両辺の発散を取ることでも確認できる。
$$\begin{aligned}\frac{1}{\mu_0}\underbrace{\mathrm{div}\,\mathrm{rot}}_{=0}\,\bm B=0=\mathrm{div}\,\bm i\end{aligned}$$
すなわち、Ampère の法則はそれ自体が $\mathrm{div}\,\bm i=0$ を表していることになる。
電荷保存則 †
$\mathrm{div}\,\bm i=0$ すなわち電流が完全にループを描いている限り、 電流が流れても正味の電荷の移動はないが、一方で 電流の湧き出し、吸い込みがあればそこには正味の電荷密度の変化が生じる。
これを端的に表したのが電荷保存則である:
$$ \underbrace{\rule[-8pt]{0pt}{0pt}\DIV\,\bm i}_\text{電流が湧き出せば}=\underbrace{\rule[-8pt]{0pt}{0pt}-\frac{\partial}{\partial t}\rho}_\text{電荷密度が低下する} $$
Ampère-Maxwell の法則 †
Maxwell は Ampère の法則を拡張し、電荷密度が時間的に変化する場合にも成り立つ法則を導いた。
$$\begin{aligned}\frac{1}{\mu_0}\mathrm{rot}\,\bm B=\bm i+\underbrace{\epsilon_0\frac{\partial \bm E}{\partial t}}_\text{変位電流}\end{aligned}$$
これは電場の時間変化も電流と同様に磁場を生むという式になっている。 この電流の次元を持つ項はしばしば変位電流と呼ばれる。
両辺の div を取ると、
$$\begin{aligned} 0&=\mathrm{div}\,\bm i+\epsilon_0\frac{\partial \mathrm{div}\,\bm E}{\partial t}\\ &=\mathrm{div}\,\bm i+\frac{\partial \rho}{\partial t}\end{aligned}$$
が得られ、これは電荷保存則に他ならない。
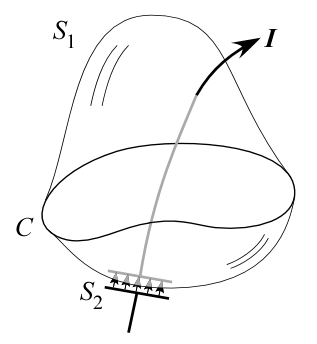
変位電流の意味するところは右図により説明される。ここでは $S_1$ を貫く電流 $I$ の経路にコンデンサが存在し、その対向電極の間を $S_2$ が通っている。このため、$S_2$ を貫く電流はゼロとなるが、 電流 $I$ によりコンデンサが充電されるため、$S_2$ 上の電場が時間と共に増加し、 $S_2$ 上では通常の電流の代わりに変位電流が流れる。
Ampère-Maxwell の法則から電荷保存則が導かれることからも分かるとおり、 $S_2$ 上を流れる変位電流はちょうど $S_1$ 上を流れる電流値と一致する。 したがって閉曲線 $C$ を貫く「電流+変位電流」は $C$ を縁とする曲面の取り方に依らず一意に定義され、 $\bm B$ の $C$ 上の周回積分の値がこの「電流+変位電流」で書かれることになる。
コメント・質問 †
添付ファイル: