量子力学Ⅰ/一次元の散乱現象
障壁よりもエネルギーが高い場合の散乱†
ここでは、自身のエネルギーよりも低い障壁や、むしろ井戸になっているようなポテンシャルへ入射する粒子について考える。古典的にはこのような障壁は粒子の進行を妨げないため常に透過するのであるが、量子論ではこのようなポテンシャルの変化によっても粒子が反射される可能性があることが分かる。
障壁よりも粒子のエネルギーが高い場合、 障壁内部の波動関数は外と同様に振動的になるが、 ポテンシャルエネルギーの分だけ運動エネルギーが減り、波長は長くなる。
同様に、障壁が負のエネルギーを持つ場合、 すなわち井戸になっている場合の評価もそのまま行える。 この場合にはポテンシャルエネルギーの分だけ運動エネルギーは増え、 井戸内の波長は外部に比べて短くなる。
先に見たトンネル現象の問題では障壁内の波動関数は指数関数的になっており、 一見すると質的に異なる問題のように感じるが、 数式の上ではトンネル現象について得た結果は粒子のエネルギーより障壁が低い場合にもそのまま適用できる。
ただ単に $\kappa=\sqrt{\frac{2m}{\hbar^2}(V_0-\varepsilon)}$ とした部分が虚数となることを加味して、
$$\kappa\to ik'$$
$$\sinh\kappa a\to -i\sin k'a$$
$$\cosh\kappa a\to \cos k'a$$
などと書き換えるだけでよい。
このとき、
$$|T|^2=\frac{1}{1+Y^2}$$
$$Y^2=\frac{V_0^2}{4\varepsilon|V_0-\varepsilon|}\sin^2 k'a$$
であるから、$\sin k'a=0$ であれば $|T|=1$ となって 100% 透過するが、 そうでない場合には有限の確率で反射されることになる。
$\sin k'a=0$ の条件は $k'\cdot a=n\pi$ すなわち、
$$k'\cdot 2a=2n\pi$$
の条件に対応するが、これは障壁中を往復するだけの距離進むと位相が元に戻る条件になっている。
このとき、
- 障壁の左端で反射した波と、
- 障壁内へ入射し、障壁の右端で反射した波と、
が打ち消し合い、$|R|$ がゼロになる。
起きる現象は $V_0>0$ の場合と $V_0<0$ の場合とで少し異なるため、個別に説明すると:
- $V_0>0$ の障壁の場合には
- 井戸の内部を進む波が右端で反射する際には位相が反転する
- 井戸の内部を戻る波は左端で元の波と反対の位相を持つ
- 入射波が井戸の左端で反射する際には位相は反転しない
- ii. の波と iii. の波が打ち消しあう
- $V_0<0$ の井戸の場合には
- 井戸の内部を進む波が右端で反射する際には位相は変化しない
- 井戸の内部を戻る波は左端で元の波と同じ位相を持つ
- 入射波が井戸の左端で反射する際に位相が反転する
- ii. の波と iii. の波が打ち消しあう
LANG: p5js_live
// =============== ここが設定
const gif_url = 'https://dora.bk.tsukuba.ac.jp/~takeuchi/?plugin=attach&refer=%E9%87%8F%E5%AD%90%E5%8A%9B%E5%AD%A6%E2%85%A0%2F%E4%B8%80%E6%AC%A1%E5%85%83%E3%81%AE%E6%95%A3%E4%B9%B1%E7%8F%BE%E8%B1%A1&openfile=scatter-vs-v0.gif';
const multi = 1; // スライダーは multi 回ループで最大値になる
const fps = 30; // 描画頻度 (frame per second)
const maxWidth = 600; // 横幅最大値
// ================ ここから下は汎用コード
let gif = null;
let frameSlider = null;
let w, h;
p.preload = () => gif = p.loadImage(gif_url);
const draw = () => {
let index = frameSlider.value();
gif.setFrame(index % gif.numFrames()); // フレームを選択して
p.image(gif, 0, 0, w, h); // 描画
}
p.setup = () => {
p.frameRate(fps);
w = Math.min(maxWidth, gif.width);
h = gif.height * w / gif.width;
p.createCanvas(w, h + 20);
frameSlider = p.createSlider(0, gif.numFrames() * multi - 1);
frameSlider.value(0);
frameSlider.position(0, h);
frameSlider.size(w);
frameSlider.input(draw);
draw();
}
p.draw = () => {
if(p.mouseIsPressed) return;
frameSlider.value((frameSlider.value() + 1) % (gif.numFrames() * multi));
draw();
}
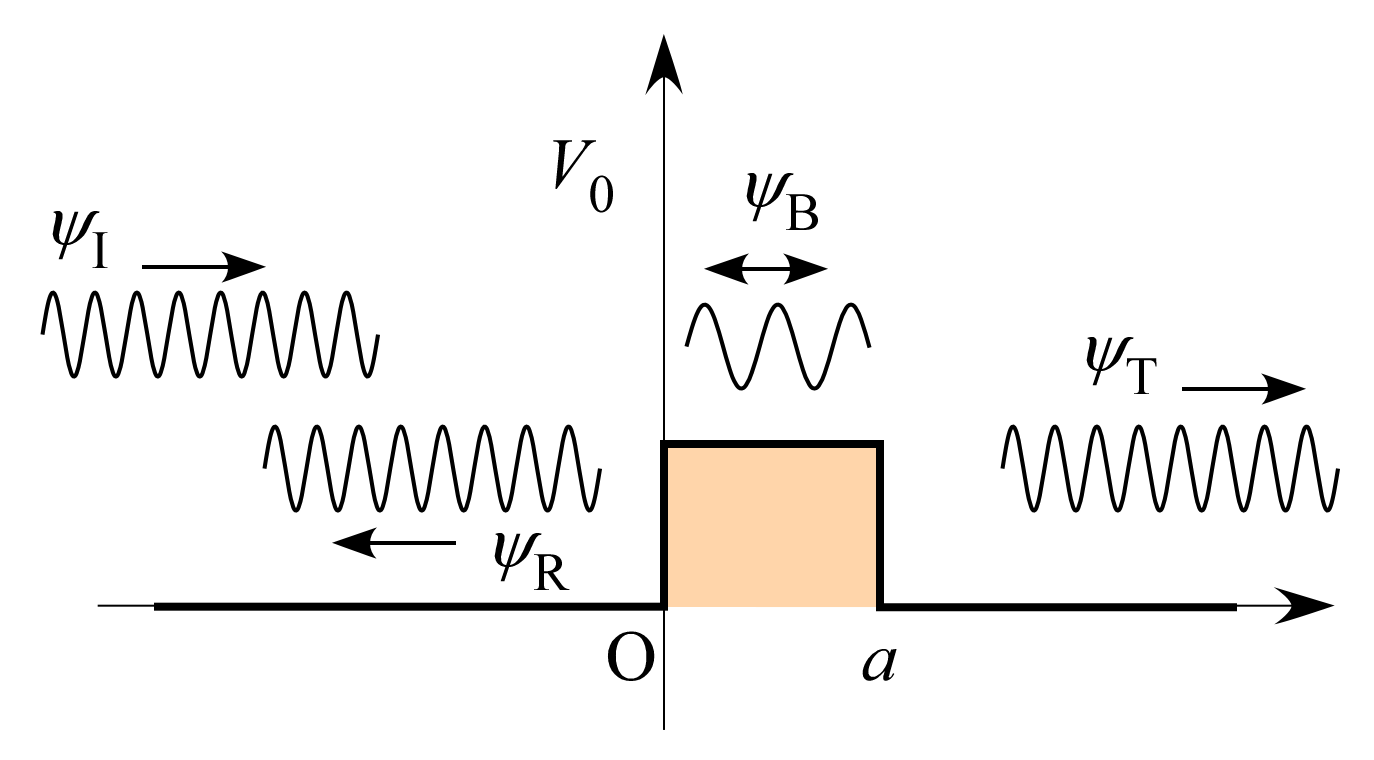
演習:ポテンシャルエネルギーの異なる領域へ入射する正弦波†
$x=0$ にて変化するポテンシャルによる散乱問題を考える。
$$V(x)=\begin{cases} 0&(x<0)\\ V_0&(0\le x) \end{cases}$$
ただし図のように、入射波を $\varphi_I(x)$、反射波を $\varphi_R(x)$、透過波を $\varphi_T(x)$ と置く。
(1) 1次元の時間によらないシュレーディンガー方程式を書き下せ。ただし波動関数を $\varphi(x)$ で表し、系のエネルギーは $\varepsilon$ ($\varepsilon>V_0$) とせよ。
(2) $\varphi(x)=e^{\pm ikx}$ ただし $k=\sqrt{2m\varepsilon/\hbar^2}$ が $x<0$ の領域での解となることを示せ。
(3) $\varphi(x)=e^{\pm ik'x}$ ただし $k'=\sqrt{2m(\varepsilon-V_0)/\hbar^2}$ が $0\le x$ の領域での解となることを示せ。
(4) $x=0$ における境界条件を $\varphi_I(x)$、$\varphi_R(x)$、$\varphi_T(x)$ を用いて書き下せ。
(5) $\varphi_I(x)=e^{ikx},\ \varphi_R(x)=Re^{-ikx},\ \varphi_T(x)=Te^{ik'x}$ と置き、(4)の方程式から $R, T$ を $k,k'$ で表せ。
(6) (5)の結果が $k|R|^2+k'|T|^2=k$ を満たすことを確かめよ。
(7) $V_0=\frac{3}{4}\varepsilon$ のときの $R,T$ を求め、(6)の関係が成り立つことを確かめよ。
(8) $V_0<0$ すなわち波長が短くなる領域に入射する条件では、界面において反射波の位相が入射波と $\pi$ だけ異なることを確かめよ。
解説†
(6) の結果は、単位時間、単位面積あたりの反射波および透過波の確率密度の流れを加えると、入射波の確率密度の流れと等しくなることに対応している。単位時間、単位面積あたりの確率密度の流量が、$S=\mathrm{Re}\left[\varphi^*(x)\frac{\hbar}{im}\frac{d}{d x}\varphi(x)\right]$ と表せることを思い出せ。
(8) の結果は屈折率の大きな領域へ入射する光の反射と同様の結果である。
ここでの結果を組み合わせて箱型ポテンシャルによる散乱問題を解くこともできる。
次図のように
$x=0$ における入射波の散乱、
$x=a$ における障壁内進行波の散乱、
$x=0$ における障壁内後退波の散乱、
のそれぞれに対して上記結果を用いると、
となり、これらをまとめることで
$$B_+=\frac{2k}{k+k'}+\frac{k'-k}{k+k'}B_-$$
$$B_-=\frac{k'-k}{k+k'}B_+e^{i2k'a}$$
$$Te^{ika}=\frac{2k'}{k+k'}B_+e^{ik'a}$$
$$R=\frac{k-k'}{k+k'}+\frac{2k'}{k+k'}B_-$$
を得る。$\lambda=k'/k$ と置いて計算すれば、
$$(1+\lambda)B_+=2-\frac{(1-\lambda)^2}{1+\lambda}e^{i2k'a}B_+$$
$$B_+=\frac{(1+\lambda)e^{-ik'a}}{(1+\lambda)^2e^{-ik'a}+(1-\lambda)^2e^{ik'a}}$$
$$B_-=\frac{(1-\lambda)e^{+ik'a}}{(1+\lambda)^2e^{-ik'a}+(1-\lambda)^2e^{ik'a}}$$
$$T=\frac{2\lambda}{(1+\lambda)^2e^{-ik'a}+(1-\lambda)^2e^{ik'a}}e^{-ika}$$
$$ \begin{aligned} R&=\frac{1}{1+\lambda}\left(1-\lambda+2\lambda B_-\right)\\ &=\frac{(1-\lambda)\{(1+\lambda)^2e^{-ik'a}+(1-\lambda)^2e^{ik'a}\}+2\lambda(1-\lambda)e^{ik'a}} {(1+\lambda)\{(1+\lambda)^2e^{-ik'a}+(1-\lambda)^2e^{ik'a}\}}\\ &=\frac{(1-\lambda)(1+\lambda)^{\cancel{2}}e^{-ik'a}+(1+\lambda)^{\cancel{2}}(1-\lambda)e^{ik'a}} {\cancel{(1+\lambda)}\{(1+\lambda)^2e^{-ik'a}+(1-\lambda)^2e^{ik'a}\}}\\ &=\frac{(1-\lambda^2)(e^{-ik'a}+e^{ik'a})} {(1+\lambda)^2e^{-ik'a}+(1-\lambda)^2e^{ik'a}}\\ \end{aligned} $$
この結果は上で得たものと等しい。
質問・コメント†
波動関数の連続性について†
匿名 ()
質問です。
ポテンシャルがデルタ関数の時、一回微分が不連続となり滑らかに接続することができないと思います。それはなぜ許されるのでしょうか?接続するための条件式だからでしょうか?
- ポテンシャルが有限高さのステップ関数である場合になぜ波動関数が滑らかに接続しなければならないかを 量子力学Ⅰ/一次元箱形障壁のトンネル#zcdcd945 で考えました。ステップ関数やデルタ関数を極限系として扱うことにより、そこでの波動関数の性質を理解することができると思います。 -- 武内(管理人)
誤植指摘†
匿名応理 ()
演習:ポテンシャルエネルギーの異なる領域へ入射する正弦波
での(3)xの範囲がx≧0だと思います。
- おっしゃるとおりでした。ご指摘ありがとうございました。 -- 武内(管理人)
添付ファイル: