量子力学Ⅰ/球面調和関数
目次 †
球面調和関数 $Y^m_l(\theta,\phi)$:角運動量の固有関数 †
全角運動量の二乗と、$z$ 軸周り角運動量との同時固有関数となる球面調和関数(球関数)の性質について学ぶ。
中心力に対する時間を含まないシュレーディンガー方程式を変数分離した際の $Y(\theta,\phi)$ に対する方程式
$$\begin{aligned} \hat\Lambda Y(\theta,\phi)=-l(l+1)Y(\theta,\phi) \end{aligned}$$
は、$Y(\theta,\phi)=\Theta(\theta)\Phi(\phi)$ と分離して、さらに
$$\begin{aligned} \frac{\partial}{\partial\phi}\Phi=im\Phi \end{aligned}$$
を満たすことを仮定すると、
$$\begin{aligned}\Phi(\phi)=\Phi_0e^{im\phi}\hspace{1cm}\text{ただし}\ \ \ \ m=0,\pm 1,\pm 2,\dots \end{aligned}$$
および、$\Theta$ に関する方程式
$$\Big[-\frac{1}{\sin\theta} \frac{\partial}{\partial \theta} \Big(\sin\theta\frac{\partial}{\partial \theta}\Big)+\frac{m^2}{\sin^2\theta}\Big]\Theta(\theta)=l(l+1)\Theta(\theta)$$
を与えることを 前項 で見た。この方程式は、$l$ が $l\ge|m|$ を満たす 整数であるときのみ解を持ち、
$$\begin{aligned} Y_l^m(\theta,\phi)= \underbrace{\rule[-15pt]{0pt}{0pt}(-1)^{(m+|m|)/2}\sqrt{\frac{2l+1}{2}\frac{(l-|m|)!}{(l+|m|)!}}P_l^{|m|}(\cos\theta)}_{\displaystyle \Theta_l{}^m(\theta)}\, \underbrace{\rule[-15pt]{0pt}{0pt}\frac{1}{\sqrt{2\pi}}e^{im\phi}}_{\displaystyle\Phi_m(\phi)} \end{aligned}$$
が、
$$\begin{aligned} \int_0^\pi \Theta_l^m(\theta)^*\Theta_{l'}^m(\theta)\,\underbrace{\sin\theta\rule[-6pt]{0pt}{0pt}}_{\text{重み}} d\theta=\delta_{ll'} \end{aligned}$$
$$\begin{aligned} \int_0^{2\pi}\Phi_m(\phi)^*\Phi_{m'}(\phi) d\phi=\delta_{mm'} \end{aligned}$$
を満たす正規直交完全な固有関数となる。この関数を 球面調和関数 と呼ぶ。*1ここでは符号を $\Theta$ に含めたが、符号を $\Phi$ に含めても、両者で分け合っても、正規直交条件を満たすことはできる
ここで、$P_l^{|m|}(\zeta)$ はルジャンドルの
$$P_l^{|m|}(\zeta)=\underbrace{(1-\zeta^2)^{|m|/2}\rule[-10pt]{0pt}{0pt}}_{\sin^{|m|}\theta}\,\underbrace{\frac{d^{|m|}}{d\zeta^{|m|}}P_l(\zeta)\rule[-10pt]{0pt}{0pt}}_{\cos\theta\text{\,の}\,l-|m|\,\text{次}}\hspace{1cm}\text{ただし\ }\zeta=\cos\theta$$
$P_l(\zeta)$ はルジャンドルの多項式で、
$$P_l(\zeta)=\frac{1}{\,2^l\,l!\,}\,\underbrace{\frac{d^l}{\,d\zeta^l\,}\underbrace{(\zeta^2-1)^l\rule[-10pt]{0pt}{0pt}}_{\zeta\,\text{の}\,2l\,\text{次}}}_{\zeta\,\text{の}\,l\,\text{次}}$$
によって与えられる。(ここでは微分方程式の解き方には踏み込まない)
|
$Y_0^0=\frac{1}{2 \sqrt{\pi }}$ $Y_1^0=\frac{1}{2} \sqrt{\frac{3}{\pi }} \cos (\theta )$ $Y_1^{\pm 1}=\mp\frac{1}{2} \sqrt{\frac{3}{2 \pi }} e^{\pm i \phi } \sin (\theta )$ $Y_2^0=\frac{1}{4} \sqrt{\frac{5}{\pi }} \left(3 \cos ^2(\theta )-1\right)$ $Y_2^{\pm 1}=\mp\frac{1}{2} \sqrt{\frac{15}{2 \pi }} e^{\pm i \phi } \sin (\theta ) \cos (\theta )$ $Y_2^{\pm 2}=\frac{1}{4} \sqrt{\frac{15}{2 \pi }} e^{\pm 2 i \phi } \sin ^2(\theta )$ |
$Y_3^0=\frac{1}{4} \sqrt{\frac{7}{\pi }} \left(5 \cos ^3(\theta )-3 \cos (\theta )\right)$ $Y_3^{\pm 1}=\mp\frac{1}{8} \sqrt{\frac{21}{\pi }} e^{\pm i \phi } \sin (\theta ) \left(5 \cos ^2(\theta )-1\right)$ $Y_3^{\pm 2}=\frac{1}{4} \sqrt{\frac{105}{2 \pi }} e^{\pm 2 i \phi } \sin ^2(\theta ) \cos (\theta )$ $Y_3^{\pm 3}=\mp\frac{1}{8} \sqrt{\frac{35}{\pi }} e^{\pm 3 i \phi } \sin ^3(\theta )$ ・・・ |
正規直交完全かつ $\phi$ での微分に対して固有関数という使い勝手の良さから、普通の周期関数をフーリエ級数展開するのと同じように、任意の $\theta,\phi$ の関数を球面調和関数で展開して処理するようなことが行われるため、これは応用数学的にも重要な関数である。
ルジャンドル多項式は、$\{1,x,x^2,x^3,\dots\}$ を、内積 $(f,g)=\int_{-1}^1 f^*(x)g(x)\,dx$ の下でシュミットの直交化により正規直交化して得られる関数系であった。→ 線形代数II/関数空間#obfa5335
$m=0$ において、$\Theta_l^0(\theta)$ はルジャンドル多項式に $\cos\theta$ を代入した形になるが、 $x=\cos\theta$ の変数変換により $dx=-\sin\theta\,d\theta$ となり、
$$\begin{aligned} (\Theta_l^0,\Theta_{l'}^0)\propto\int_0^\pi P_l^*(\cos\theta)P_{l'}(\cos\theta)\sin\theta\,d\theta &=\int_1^{-1} P_l^*(x)P_{l'}(x)\,dx \end{aligned}$$
となることから、$\Theta_l^0(\theta)$ の直交性はルジャンドル多項式の直交性から直接導かれる。 同様に、$\Theta_l^m(\theta)$ の直交性もルジャンドル陪関数の直交性から導かれる。
特徴 †
$$Y_l^m(\theta,\phi) \propto \underbrace{(\sin\theta)^{|m|}\rule[-6.6pt]{0pt}{0pt}}_{0,\pi\text{に}|m|\text{重根}}\underbrace{\Big[\cos\theta\,\text{の}\,l-|m|\,\text{次多項式}\Big]}_{0\,<\,\theta\,<\,\pi\,\text{に}\,l-|m|\,\text{個の根を持つ}}e^{im\phi}$$
の形になっている。
- $\phi$ 依存性は $e^{im\phi}$ なので、$0\le\phi\le 2\pi$ で $|m|$ 回振動する
- 絶対値 $|Y_l^m|$ は $\phi$ に依存しない
- $\Theta_l^m$ は
- $\theta=0,\pi$ に $|m|$ 重根を持つ
- $0<\theta<\pi$ に $l-m$ 個の単根を持つ
- つまり、$0\le\theta\le\pi$ に $l+1-m$ 個の山を持つ
「振動が多い = 運動量が大きい」であることを考えると、 $\Phi$ が $m$ 回、$\Theta$ が $l+1-m$ 回振動し、合わせて $l+1$ になる 全角運動量 $l$ を $z$ 軸周り成分とその他とに分けたことに対応する。
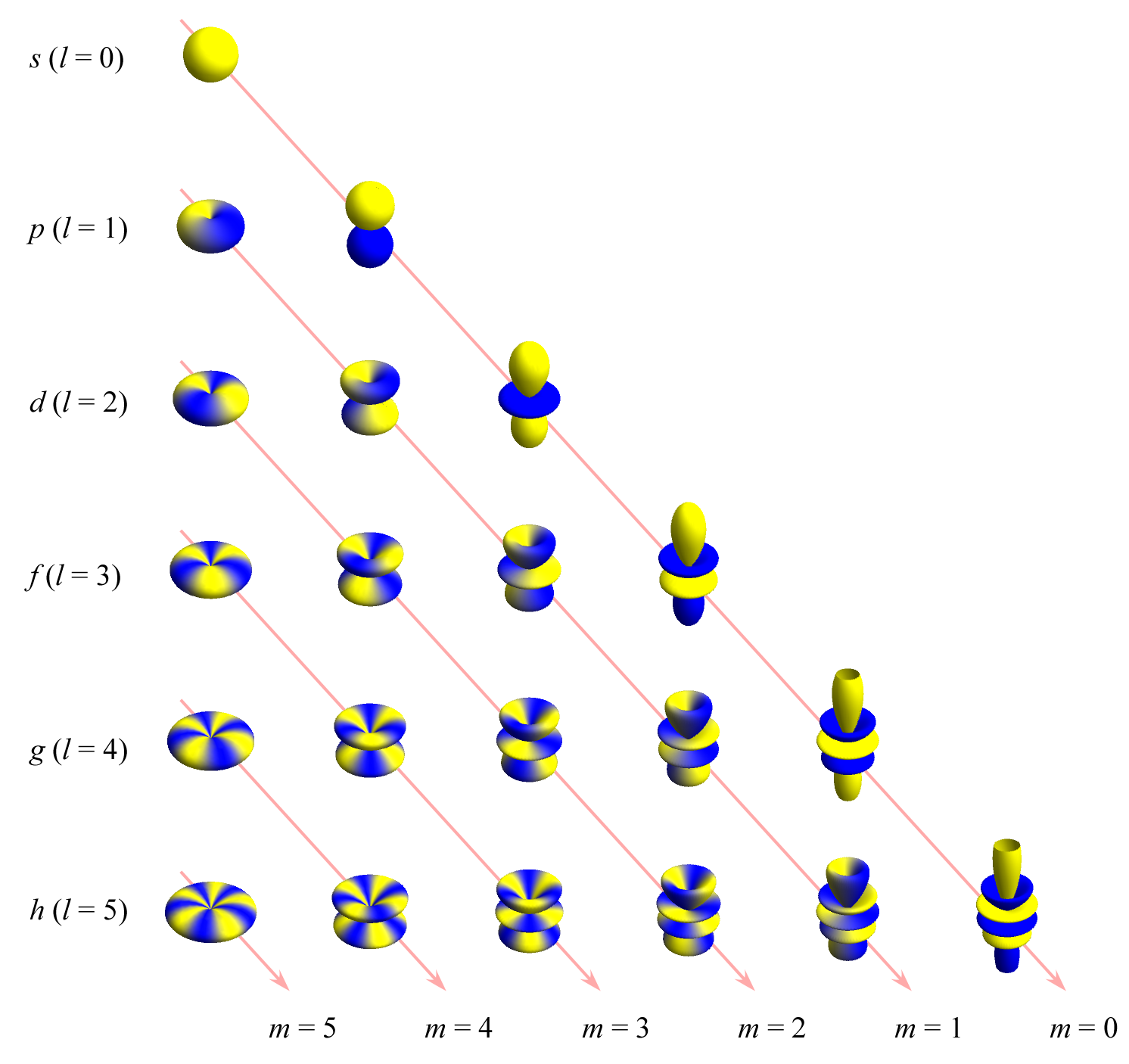
形状 †
$|\Theta_l^m(\theta)|$ の形状は次のようになる。
ここでは縦軸に $\theta$ を取り、右方向に $|\Theta_l^m(\theta)|$ を取った。
- グラフは左から、$l-m=0,1,2,3,4$ に相当する。$l-m$ が増えると山の数が増える = $x,y$軸周りの角運動量が大きくなる。
- 1つのプロットの中では $m=0,1,2,3,4$ のグラフを重ねて示した。
- $m$ が増えると $\theta=0,\pi$ 付近の立ち上がりが遅くなり、山が中央に寄る。
- これは $l_z$ が大きくなることで遠心力により分布が扁平になったことに対応する。
上と同じものを動径プロットにしたのが次のグラフである。 (原点から $\theta$ の向きに $|\Theta_l^m(\theta)|$ だけ離れた点を結んだ曲線)
さらに $\phi$ 依存性も合わせて表示するため、 $\theta,\phi$ 方向別に原点から $|Y_l^m(\theta,\phi)|$ の距離の点を結ぶ曲面をプロットしたのが次の図である。 色は複素数としての位相 $\mathrm{arg}\,Y_l^m(\theta,\phi)$ を表しており、黄色が+1、青が-1に対応する。
- $\Theta$ は実数関数である
- $\Phi$ は位相を回転させるだけで大きさを変えない
- そのため絶対値のプロットは $z$ 軸を中心とする回転体となり、また、$Y_l^m$ と $Y_l^{-m}$ は同じ形になる
- 位相 ($\Phi$ で決まる) は
- $\phi$ が一周する間に $m$ 回だけ回転する。
- $Y_l^m$ と $Y_l^{-m}$ とは $xz$ 平面に対して対称になる
- 形状 ($\Theta$ で決まる) は
- $\theta$ 方向は隣り合う突出部で符号が反転することから、位相も反転する
- $l-m$ が等しいもの(上図で縦に並んだもの)について形状が似ている
- $\theta$ 方向に $l-m+1$ 個の突出部が見られる。
- これらは $l^2-l_z^2=l_x^2+l_y^2$ が等しい状態である
- $l-m$ が等しいもの同士では、$m$ が大きくなるほど扁平になり、半径も大きくなる。$l_z$ が大きくなるため遠心力により引き延ばされている。
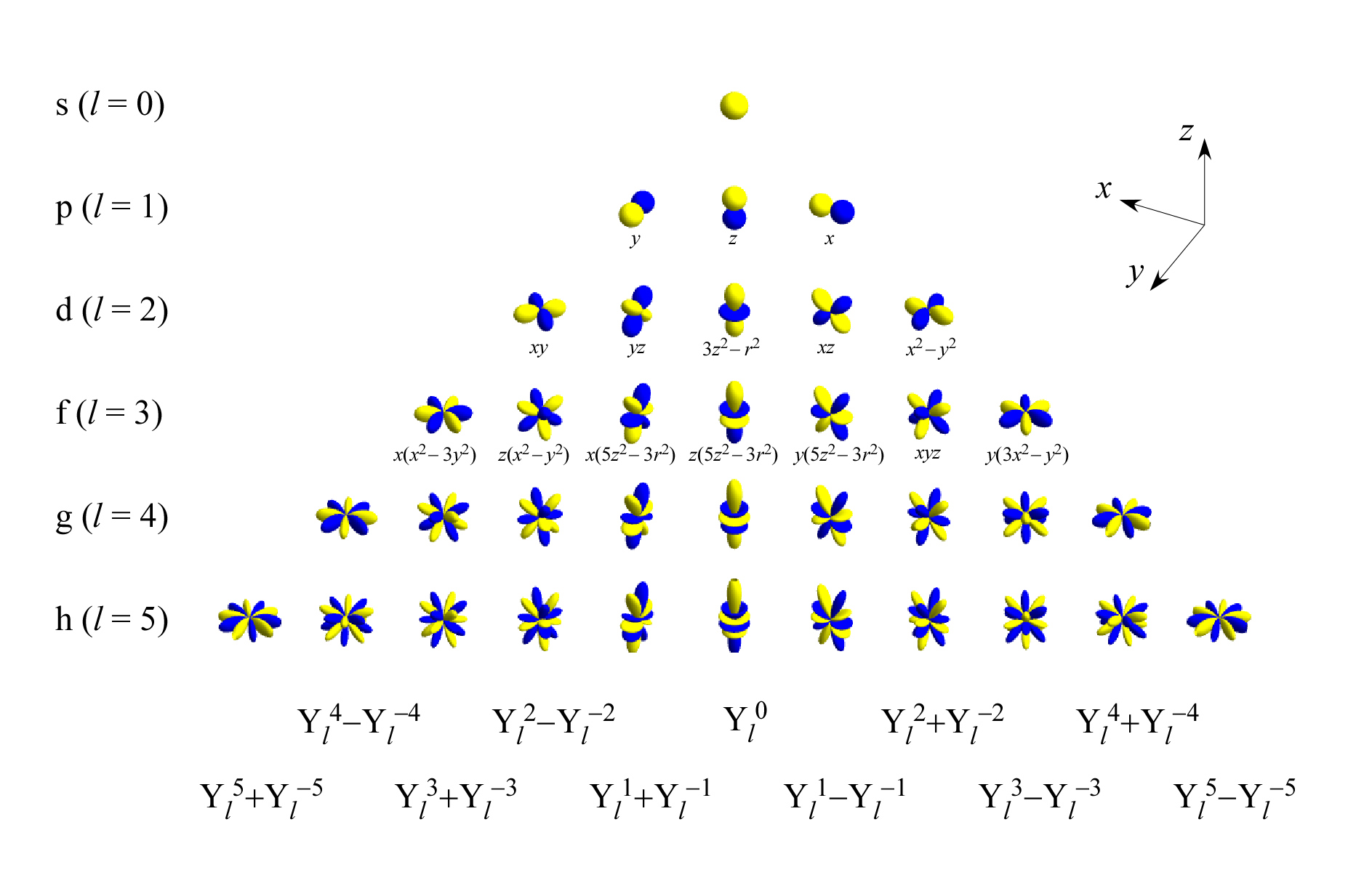
$x,y,z$ との関係 †
$Y_l^m$ は位相成分 $e^{im\phi}$ を含むため、$m\ne 0$ に対しては必然的に複素関数となる。
一方、$Y_l^m\pm Y_l^{-m}$ を作れば、
$$\begin{aligned}Y_l^m\pm Y_l^{-m}\propto e^{im\phi}\pm e^{-im\phi}\propto \sin m\phi,\cos m\phi\end{aligned}$$
であり(ただし、複合の順序は両辺で必ずしも一致しない)、係数を適当に選ぶと全体を実数関数にできる。
以下に例を挙げる:
$p\ (l=1)$ 状態 †
$$\begin{aligned}\begin{array}{lll} {}-(Y_1{}^{1}-Y_1{}^{-1}) &\propto \sin\theta\cos\phi&\propto x/r\\ i(Y_1{}^{1}+Y_1{}^{-1})&\propto \sin\theta\sin\phi&\propto y/r\\ Y_1{}^0 &\propto \cos\theta&\propto z/r\\ \end{array} \end{aligned}$$
であるから、これらの軌道は $p_x,p_y,p_z$ と呼ばれる。
$d\ (l=2)$ 状態 †
$$\begin{aligned} \begin{array}{lll} {}-i(Y_2{}^{2}-Y_2{}^{-2})&\propto \sin^2\theta\sin 2\phi&\propto xy/r^2\\ i(Y_2{}^{1}+Y_2{}^{-1})&\propto \sin\theta\cos\theta\sin\phi&\propto yz/r^2\\ {}-(Y_2{}^{1}-Y_2{}^{-1}) &\propto \sin\theta\cos\theta\cos\phi&\propto zx/r^2\\ (Y_2{}^{2}+Y_2{}^{-2}) &\propto \sin^2\theta\cos 2\phi&\propto (x^2-y^2)/r^2\\ Y_2{}^{0} &\propto 3\cos^2\theta-1&\propto (3z^2-r^2)/r^2 \end{array} \end{aligned}$$
であるから、これらの軌道は $d_{xy},d_{yz},d_{zx},d_{x^2-y^2},d_{3z^2-r^2}$ などと呼ばれる。
同様に、
$$\begin{aligned}Y_1{}^{1}\propto (x-iy)/r\end{aligned}$$
のように $Y_l^m$ を $x,y,z$ で表すことも可能である。
実関数表示 †
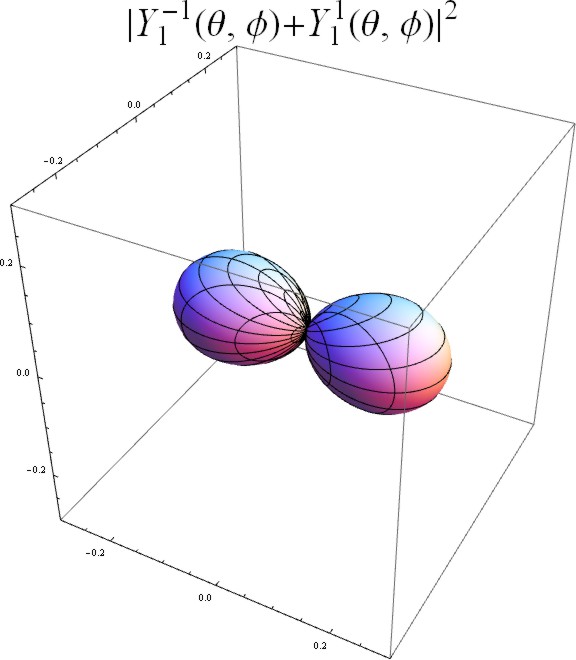
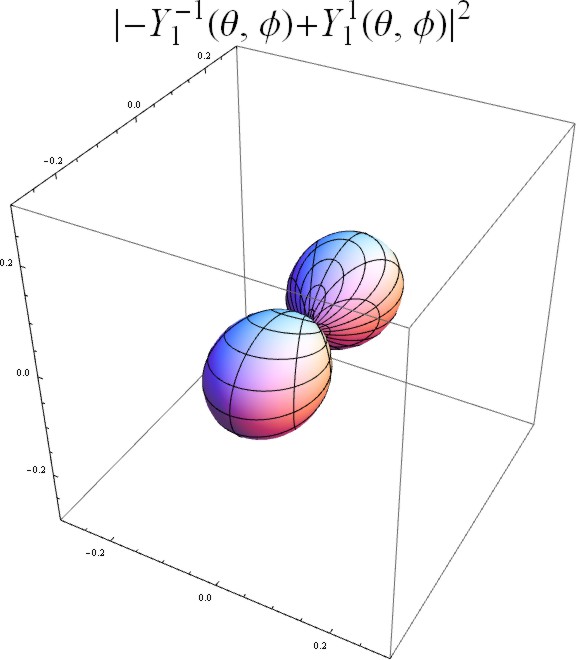
以下に $(Y_l^m\pm Y_l^{-m})/\sqrt{2}$ をプロットした。($m=0$ についてはそのまま $Y_l^0$ をプロットした)
$\cos m\phi$ と $\sin m\phi$ は互いに直交するため、これらの関数も正規直交系をなす
この表示から、$\phi$ 方向に $m$ 個、$\theta$ 方向に $l-m+1$ 個の突出部を持つことが明確に読み取れる。
実際にこれらをキレイな形の実関数とするためには符号に注意する必要があり、正確な表示は次のようになる。
$$\begin{aligned} \Psi_l^m=\begin{cases} i\Big\{(-1)^{|m|}Y_l^{|m|}-Y_l^{-|m|}\Big\}/\sqrt 2\hspace{4mm}&(m<0)\hspace{5mm}\propto\ \sin m\phi\\ \hspace{1cm}Y_l^0&(m=0)\hspace{4mm}\propto \ \ \ 1\\ \Big\{(-1)^{|m|}Y_l^{|m|}+Y_l^{-|m|}\Big\}/\sqrt 2&(m>0)\hspace{4mm}\propto\ \cos m\phi\end{cases} \end{aligned}$$
これらの関数は、$l_z=\hbar m$ の状態と $l_z=-\hbar m$ の状態とを等しい重みで重ね合わせたものであるので、もはや $l_z$ の固有状態ではなく、$l_z$ を測定すれば等確率で $\pm\hbar m$ のどちらかの値を取る。したがって、$\overline{l_z}=0$ である。
隣り合う突出部で波動関数の符号が反転している理由は下図を参照せよ。
$z$ の特殊性 †
球面調和関数は $\hat l^2$ および $\hat l_z$ の同時固有関数となるように取られているため、 表式の上では $z$ が特殊な方向となっている。しかし、
$$\begin{aligned} \begin{array}{lll} p_x:\ \Psi_1{}^1\hspace{2.3mm}=(-Y_1{}^{1}+Y_1{}^{-1})/\sqrt{2} &\propto \sin\theta\cos\phi&\propto x/r\\ p_y:\ \Psi_1{}^{-1}=i(Y_1{}^{1}+Y_1{}^{-1})/\sqrt{2}&\propto \sin\theta\sin\phi&\propto y/r\\ p_z:\ \Psi_1{}^0\hspace{2.3mm}=Y_1{}^0 &\propto \cos\theta&\propto z/r\\ \end{array} \end{aligned}$$
のようにして作った $p_x, p_y$ が $p_z$ と異なる方向を向いているものの、まったく同じ形になることからも分かるとおり、 中心力に対するシュレーディンガー方程式自体は当然等方的であり、その解も $z$ 方向を特別な方向としているわけではない。
実際、ある特定の $l$ に対する $2l+1$ 個の関数 $\{Y_l{}^{m}\}\ (m=-l,-l+1,\dots,l-1,l)$ を用いることで、$\hat l^2=\hbar^2l(l+1)$ となる「任意の関数」をこれらの線形結合(重ね合わせ)で表現できる。
言い換えると、$\hat l^2$ の固有値 $\hbar^2l(l+1)$ の固有空間は $2l+1$ 次元であり、 $\{Y_l{}^{m}\}\ (m=-l,-l+1,\dots,l-1,l)$ はその空間に取った正規直交完全系である。
この正規直交完全系のそれぞれが $\hat l_z$ の固有関数であるように選んだために $z$ が特殊な方向になったのである。
このことを示すように、同じ $l$ に属する $2l+1$ 個の固有関数の確率密度をすべて足し合わせてしまえば、次のように球対称な定数関数が得られる。これは、仮想的に全ての $\{Y_l{}^{m}\}\ (m=-l,-l+1,\dots,l-1,l)$ に1つずつ電子が入るなら、その電荷密度は空間的に等方的に分布することを示している。
$$\begin{aligned}\sum_{m=-1}^l|Y_l^m(\theta,\phi)|^2=\frac{2l+1}{4\pi}\end{aligned}$$
演習:$m$ に関する漸化式 †
$\displaystyle\begin{aligned}\Phi_m(\phi)=\frac{1}{\sqrt{2\pi}}e^{im\phi}\end{aligned}$ より、 $e^{\pm i\phi}\Phi_m(\phi)=\Phi_{m\pm 1}(\phi)$
一方、$Y_l{}^m(\theta,\phi)=\Theta_l{}^m(\theta)\Phi_m(\phi)$ を $Y_l{}^{m\pm 1}(\theta,\phi)=\Theta_l{}^{m\pm 1}(\theta)\Phi_{m\pm 1}(\phi)$ に変換するには、先に導入した演算子
$$\begin{aligned}\hat l_\pm=\hat l_x\pm i\hat l_y\end{aligned}$$
が役に立つ。 具体的には $m$ に対する次の漸化式が成り立つ。
$$\begin{aligned} \begin{cases} \,\hat l_+\,Y_l{}^{m}(\theta,\phi)=\hbar\sqrt{(l-m)(l+m+1)}\,Y_l{}^{m+1}(\theta,\phi)\\ \,\hat l_-\,Y_l{}^{m}(\theta,\phi)=\hbar\sqrt{(l+m)(l-m+1)}\,Y_l{}^{m-1}(\theta,\phi)\\ \end{cases} \end{aligned}$$
すなわち、$\hat l_\pm$ は量子数 $m$ を1だけ増やす/減らす演算子になっている。
(1) $Y_l{}^m$ の $m$ は $-l\le m\le l$ の範囲に入らなければならなかった。 $m=\pm l$ のとき、さらに1だけ $m$ を増やそう/減らそうとすると何が起きるか? 上記の漸化式を元に確かめよ。
(2) $Y_l{}^m$ は $\hat l_x,\hat l_y$ の固有関数でも、$\hat l_+,\hat l_-$ の固有関数でもないが、$\hat l_+\hat l_-$ や $\hat l_-\hat l_+$ の固有関数になっている。 その固有値を求めよ。
(3) $\frac{1}{2}\left( \hat l_+\hat l_-+\hat l_-\hat l_+\right)=\hat l_x^2+\hat l_y^2$ となることを確かめよ
(4) (2),(3) の結果を用いて $\left(\hat l_x^2+\hat l_y^2\right)Y_l{}^m=\hbar^2(l^2-m^2+l)Y_l{}^m$ を示せ。
解説 †
(1) から分かるように、 通常、固有関数に生成・消滅演算子を適用すると、量子数を1だけ増やしたり、 減らしたりした固有関数が得られるのであるが、 量子数の取りうる範囲が限られているとき、その範囲を超えて量子数を増減させようとすると、 演算結果はゼロになってしまい、有効な固有関数を生成しない。 これは生成・消滅演算子が一般的に持つ性質である。
調和振動子では下降演算子と上昇演算子の合成 $\hat a^\dagger\hat a$ は数演算子 $\hat n$ として働き、 波動関数から量子数を取り出すのに使えたが、(2) から分かるように $\hat l_+\hat l_-$ は数演算子にはならない。ボゾンやフェルミオンで $\hat a^\dagger\hat a$ が数演算子 $\hat n$ として働くのはボゾンやフェルミオンの生成・消滅演算子が持つ特異な交換関係 $\hat a\hat a^\dagger\pm\hat a^\dagger\hat a=1$ に依存していることを知っておくように。
(4) より、$Y_l{}^m$ は $\hat l^2$ および $\hat l_z$ の固有関数であると共に、 $\hat l_x^2+\hat l_y^2$ の固有関数でもある。(ただし、$\hat l_x^2$ や $\hat l_y^2$ の固有関数ではない)
このことは、次のように書き表してみると明らかである。
$$\begin{aligned} \underbrace{\hat l^2}_{\hbar^2l(l+1)}Y_l{}^m= (\underbrace{\hat l_x^2+\hat l_y^2}_{\hbar^2(l^2+l-m^2)}+ \underbrace{\hat l_z^2}_{\hbar^2m^2})Y_l{}^m \end{aligned}$$
すなわち、上記 (4) の結果は $\hat l^2Y_l{}^m=\hbar^2l(l+1)Y_l{}^m$ と $\hat l_zY_l{}^m=\hbar mY_l{}^m$ とから直接導けるものである。
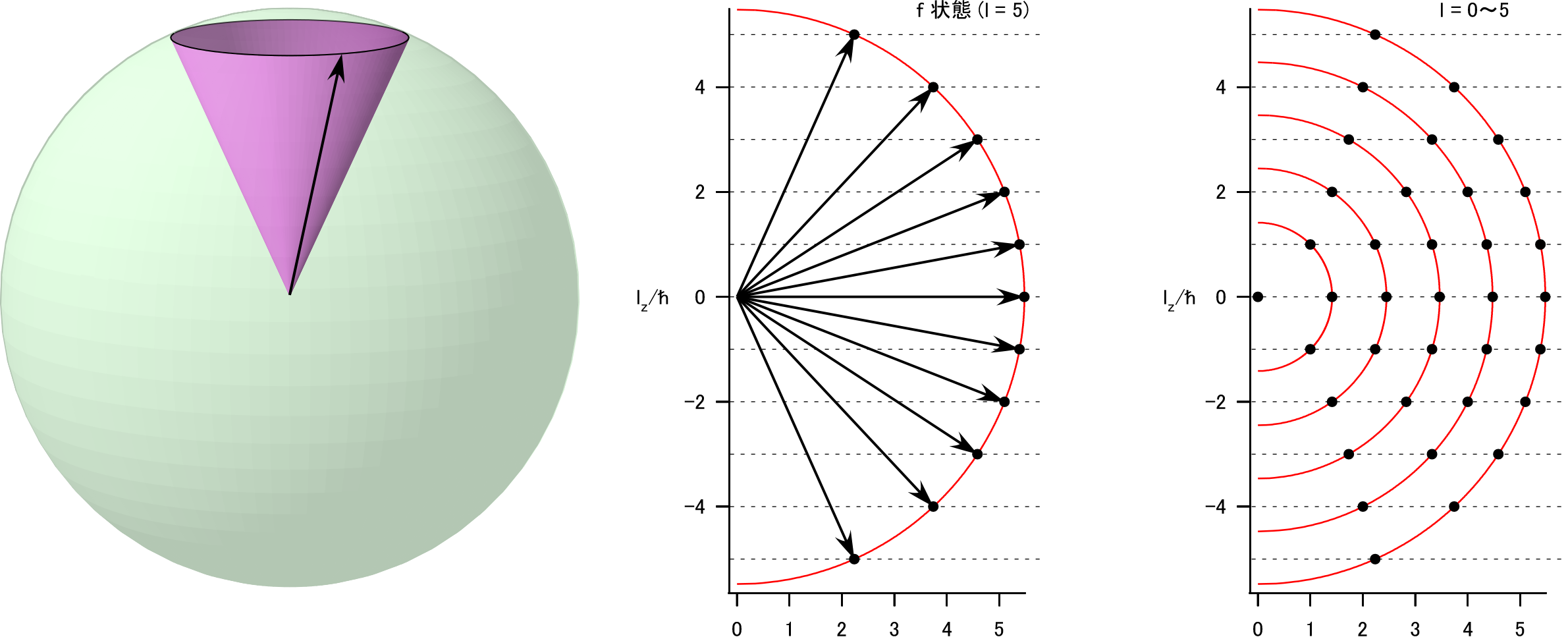
この関係を図形的に理解しよう。
たとえば $l=5$ に対応する f 状態では $\hat l^2=\hbar^2 5(5+1)$ であるから、 対応する角運動量ベクトル $\bm l$ は半径 $|\bm l|=\hbar \sqrt{30}$ の球面上にある。
この状態に対して適当な方向に $z$ 軸を取ると、角運動量のその方向の成分 $l_z$ は 全角運動量 $|\bm l|^2$ と同時に確定値を取ることができて、その値は $m=-l,\dots,l$ に対応する $2l+1$ 個の値を取りうる。
例えば $l=5,m=5$ の状態に対しては $\hat l^2=30\hbar^2, \hat l_z=5 \hbar$ が確定し、 さらに $\hat l_x^2+\hat l_y^2=\hat l^2-\hat l_z^2=30\hbar^2-(5\hbar)^2=5\hbar^2$ が確定するものの、 $\hat l_z$ と非可換な $\hat l_x$ や $\hat l_y$ 自体は、 $\langle l_x\rangle=\langle l_y\rangle=0$ のように期待値がゼロであることはわかるものの、 ${\sigma_{l_x}}^2+{\sigma_{l_y}}^2=\hat l_x^2+\hat l_y^2=5\hbar^2$ であるから、 それぞれの値は完全に不定となる。
すなわち、角運動量ベクトル $\bm l$ は左図に示した紫の円錐と球との交線上にあることになる。
他の $m$ についてもそのような円錐を考えることができ、その方向は中図に示したようになる。
$l$ は全角運動量を決める量子数であるため、(軌道)角運動量量子数 あるいは 軌道量子数と呼ばれる。また歴史的経緯により 方位量子数 と呼ばれることもある。
一方、$m$ はこれが原子内での電子の運動を表す場合には $z$ 方向への磁化を決める量であるため、(軌道)磁気量子数と呼ばれる(荷電粒子である電子の磁気モーメントは角運動量に比例するため)。
量子数の名前に(軌道)と付いているのは、スピン(角運動量)量子数やスピン磁気量子数と区別する際に用いるためだ。
方位量子数という名前について †
「方位量子数」は英語で Azimuthal Quantum Number といい、Azimuth という単語を方位と訳したのがこの名前だ。
通常 Azimuth とは角度 $\phi$ のことを表すので、この名前はむしろ $l_z$ に相当する量子数である $m$ にこそふさわしい感じがして、紛らわしいのだが、どうやらこの命名は歴史的経緯によるものであるらしい。
この量子数を導入したアルノルト・ゾンマーフェルトも始めは Azimuth を $z$ 軸周りの角度の意味で使っていたのであるが、後に「(原子核の周りを惑星のように一定の軌道を描いて回転する電子の)軌道面上で測った角度」の意味で使い始め、 結果的に Azimuthal Quantum Number が「軌道面に垂直な軸周りの角運動量」すなわち「全軌道角運動量」 を表す量子数を指すようになったらしい。*2https://hsm.stackexchange.com/... を鵜呑みにした解説なのだけれど、、、信憑性は高そう?
非常に紛らわしいので、特に国内では「軌道量子数」「(軌道)角運動量量子数」との呼び方が一般的になりつつある。
質問・コメント †
質問 †
こいけ? ()
球面調和関数Y(θ,φ):角運動量の固有関数
の項の最後から4行目が
dx=sinθdθではなくdx=-sinθdθではないでしょうか?
- おっしゃる通りでした。修正いたしました。 -- 武内(管理人)?
球面調和関数の実数化 †
質問? ()
なぜ、確率密度の分布を考える際に、球面調和関数の2乗ではなく、実数化した球面調和関数の2乗を考えるのでしょうか?
言い換えると、球面調和関数の実数化は何を目的として、行っているのでしょうか?
理解が浅く、的を得ていない質問であるかもしれませんが、よろしくお願いします
- 球面調和関数の虚数版と実数版との関係は、フーリエ級数の虚数版 $e^{\pm ikx}$ と実数版 $\sin kx,\cos kx$ との関係に似ていると考えるといいと思います。複素関数を念頭に置く場合には複素版がふさわしいけれど、主に実数関数を考える場合には実数系がふさわしい。また、実数系は $x,y,z,r$ で書き換えることのできるため、そういう意味でも重畳されますね。化学の時間に $p_x$ 軌道や $d_{xy}$ 軌道などというのが出てきたと思いますが、それらが実数版の関数系と対応しています。 -- 武内(管理人)?
*1 ここでは符号を $\Theta$ に含めたが、符号を $\Phi$ に含めても、両者で分け合っても、正規直交条件を満たすことはできる
*2 https://hsm.stackexchange.com/questions/7107/why-is-the-azimuthal-quantum-number-so-named を鵜呑みにした解説なのだけれど、、、信憑性は高そう?
添付ファイル: