量子力学Ⅰ/箱の中の自由粒子
目次 †
概要 †
シュレーディンガー方程式を解くという問題は数学的に難しく、 解析的な関数として解が得られるような問題は非常に限られている(それ以外は数値的に、あるいは近似的に解くが、それでも精度の高い計算には困難を伴う)。
この授業では、最も簡単ないくつかの例について時間に依存しないシュレーディンガー方程式を解き、 定常的な解を求めながら、普通の(難しい)問題にも共通する 波動関数の一般的性質 について学ぶ。
復習 †
時間に依らないシュレーディンガー方程式:
$$ \left(-\frac{\hbar^2}{2m}\nabla^2+V(\bm r)\right)\varphi(\bm r)=\varepsilon\varphi(\bm r) $$
確率密度が時間によって変化しない解:
$$\psi(\bm r,t)=e^{-i\varepsilon_kt/\hbar}\varphi_k(\bm r)$$
ただし $\varepsilon_k$ は上記方程式の固有値、$\varphi_k(\bm r)$ はそれに対応する固有関数。
演習:1次元の箱の中の自由粒子 †
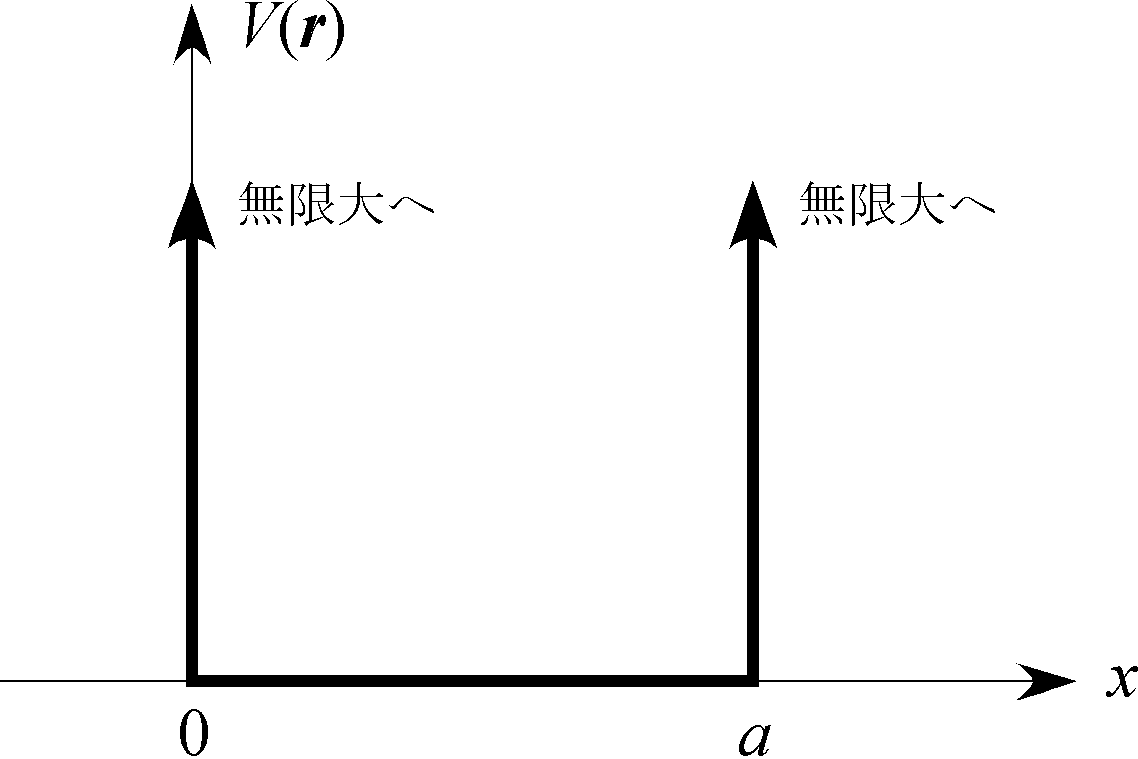
$a$ を正の定数として、$0<x<a$ の領域に閉じ込められた電子の定常状態を考える。
このような状況は、上記の範囲内で $V(x)=0$、範囲外で $V(x)=+\infty$ と仮定することで実現され、井戸型ポテンシャルの問題とも呼ばれる。
(1) 箱の中の領域での、時間に依存しない一次元シュレーディンガー方程式を書け。 (一次元なので $\bm r\to x$、$\bm\nabla\to d/dx$ とすればよい。 また、上記の通り箱の中では $V(x)=0$ である。)
(2) $\varphi(\bm r)=Ae^{ikx}+Be^{-ikx}$ の形の波動関数が (1) の解となることを確かめ、 $k$ の値を定めよ。 この式は2つの任意パラメータを含むから、(1)で求めた2階の微分方程式に対する一般解である。
(3) 箱の外では $\varphi(x)=0$ となる。その理由を答えよ。
(4) 波動関数には連続性が要求されるため、箱の内側でも壁面において $\varphi(x)=0$ でなければならない。 この境界条件を満たすために $k$ に課される条件を 任意の自然数を表わす変数 $n$ を用いて書け。 *1通常は $\varphi$ の1次微分 $d\varphi/dx$ も連続となるが、ここではポテンシャルの無限大の不連続性を反映して微係数は不連続になる
以下、$n$ で指定される $k$ を $k_n$、 対応する波動関数を $\varphi_n(x)$、 対応するエネルギー固有値を $\varepsilon_n$ と書く。 このように離散化した固有値や固有関数を指定する指標 $n$ は 量子数と呼ばれる。
(5) $\varepsilon_n$ を求めよ。
(6) $\varphi_n(x)$ を求めよ。ただし、規格化すること。
(7) $\varphi_n(x)$ に対応する、 時間に依存するシュレーディンガー方程式の解 $\psi_n(x,t)$ を求めよ。
(8) $\psi_n(x,t)$ に対して、$\overline x,\sigma_x,\overline p,\sigma_p$ を求めよ。
解説 †
固有値の離散化 †
上の問題を顧みると、
時間に依らないシュレーディンガー方程式は $\hat H\varphi(\bm r)=\varepsilon\varphi(\bm r)$ の形をしており、行列の固有値問題 $A\bm x=\lambda \bm x$ と非常に似た形をしていることが分かる。事実、関数をベクトルとみなす関数空間の考え方からすると(後で詳しく復習する)、文字通り線形変換 $\hat H$ に対する固有値問題となっており、そのためこの $\varepsilon$ を固有値、解となる波動関数 $\varphi$ を固有関数と呼ぶ。
時間に依らないシュレーディンガー方程式は具体的には位置座標に対する2次微分方程式となり、 境界条件を考えなければ任意の $\varepsilon$ (複素数でさえ)に対して解が見つかった。 → (2)
そこに境界条件を課すと解の一般形に含まれるパラメータが 量子数を含む形で書かれ、その結果としてエネルギー固有値が離散化し、同時に実数に限られた。 → (4)
離散化したエネルギー固有値をエネルギー準位あるいはエネルギーレベルなどと呼ぶ。
一般に束縛された電子では系の境界において波動関数がゼロとなる条件が課され、 その条件のために離散化した固有値が現れる。
一方で、束縛されていない場合にはそのような境界条件が存在せず、連続的な固有値が現れる。 例えば全空間で自由な場合の平面波には波数の制限はなく、エネルギー(運動エネルギー)も任意の値を取りうる。 ただしそのように全空間に広がった波動関数に対しては通常の意味での規格化はできず、 現実的な系に対する数学的に厳密な解とはなり得ない。
一方、上の例でも箱をどんどん大きくしていくと、離散化したエネルギー準位の間隔は徐々に狭まるから、 箱がある程度以上大きくなればエネルギーや波数は実質的に連続値を取れるようになる。
波動関数の形 †
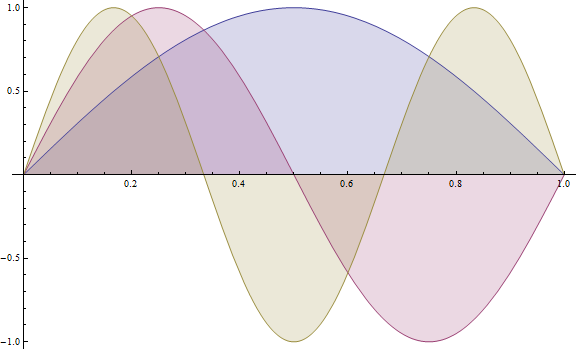
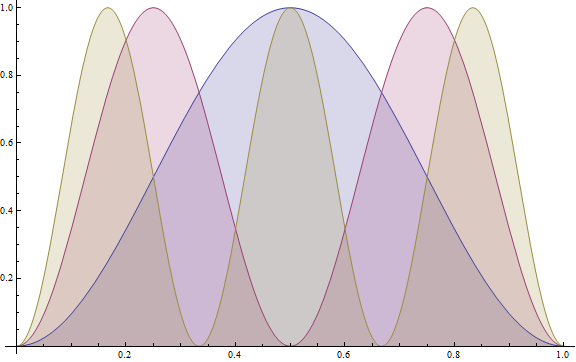
下のグラフは $\varphi_n(x)$ と $|\varphi_n(x)|^2$ を表わしており、 $n=1,2,3$ の場合を示している。
$n$ 番目の固有関数は $n$ 個のピークと $n-1$ 個の
ポテンシャル井戸の中心を基準とすれば、$n$ が奇数の時は偶関数、偶数の時は奇関数となっている。 実は $x=0$ に対して 対称なポテンシャルに束縛されたエネルギー固有関数は必ず偶関数または奇関数の形になる ことを証明可能である。→ 詳しくは [箱の中の自由粒子/メモ]
定常状態の運動エネルギーと運動量 †
$n$ が大きいほどエネルギーが高くなるが、波動関数が値を持つ全領域で $V(x)=0$ であるから、 そのエネルギーはすべて運動エネルギーである。このように「定常状態」 が運動エネルギーを持つとはどういうことであろうか?
ここで見たような「エネルギー障壁」に閉じ込められた粒子は、古典論では2つの「弾性壁」に挟まれた空間を一定周期で壁にバウンドしながら往復運動する系に対応する。弾性衝突で速さは変化せず向きだけが変わるため、運動エネルギーは時間に対して変化しないものの、運動方向は周期的に変化する。
一方、後に学ぶ方法を用い、「$\varphi_n(x)$ で表される状態($n>1$)」に対して運動量を測定した際に得られる運動量の確率分布を求めれば、$+n\pi\hbar/a$ 程度の値、あるいは $-n\pi\hbar/a$ 程度の値、が半々の確率で得られることが分かる。$\overline p=0$ はそれらの平均(= 期待値)がゼロであることを表わしており、$\sigma_p^2=\overline{\ p^2\ }=(n\pi\hbar/a)^2$ もこのことと対応している(ただし確率分布は幅を持ち、必ずしも $|p|=n\pi\hbar/a$ ピッタリにはならないこと、$n=1$ では $p=0$ となる確率が最も高いこと、など、一筋縄ではいかないところもある)。 → 詳しい導出については 量子力学Ⅰ/箱の中の自由粒子/メモ#t79c9512 を参照のこと。
運動量を測定した際に正と負のどちらの値が得られるかが本質的に決まらないというような 不確定性 が量子力学の特徴である。例えば、ある時点で測定した運動量が正の値であれば、直後にもう一度運動量を測定すればやはり正の値が測定される可能性が高そうに思える。しかし、位置や運動量などの物理量を測定するためには電子と計測器との間に何らかの相互作用が必要であり、定常状態を求める際に仮定した $V(x)$ はそのような相互作用の影響を含んでいない。つまり、測定を行うことにより $V(x)$ が変化するため測定前の量子状態は壊れてしまう。すなわち、ある量子状態に対する測定は最大1回しか行えない。その1回の測定で得られる位置や運動量の確率分布が、先に学んだように波動関数により与えられるのである。
ゼロ点運動 †
$n=1$ は最低エネルギーの状態を表わしており、そのような状態は 基底状態 と呼ばれる。 これに対して、$n>1$ は 励起状態 と呼ばれる。
興味深いことに、定常状態の中でもさらに $n=1$ となる基底状態においてさえ、系は有限の運動エネルギーを持っている。
$$\varepsilon_1=\frac{\hbar^2 \pi^2}{2ma^2}$$
基底状態における運動を ゼロ点運動 あるいは ゼロ点振動、エネルギーを ゼロ点エネルギー と呼ぶ。
$\varepsilon\propto 1/a^2$ のように、 電子を 狭い場所に閉じ込めると運動エネルギーが大きくなる ことも覚えておくように。
非定常状態の解 †
定常状態の重ね合わせで非定常状態を作れる †
異なるエネルギーを持つ定常状態の解を複数加え合わせることで非定常状態の解を作れる。
例として、基底状態と第一励起状態の解を加えた次の関数を考えよう。 係数の $1/\sqrt 2$ は規格化定数である。*22つの直交するベクトルを加えて規格化する際の係数が $1/\sqrt 2$ であったことを思い出そう
$$\begin{aligned} \psi(x,t)&=\frac{1}{\sqrt 2}\big(\psi_1(x,t)+\psi_2(x,t)\big)\\ &=\frac{1}{\sqrt 2}\big(e^{-i\varepsilon_1t/\hbar}\varphi_1(x)+e^{-i\varepsilon_2t/\hbar}\varphi_2(x)\big) \end{aligned} $$
この関数が時間を含むシュレーディンガー方程式の解となることは、シュレーディンガー方程式が線形であることと、$\psi_1(x,t),\psi_2(x,t)$ がそれぞれシュレーディンガー方程式の解であることからすぐに導かれる。
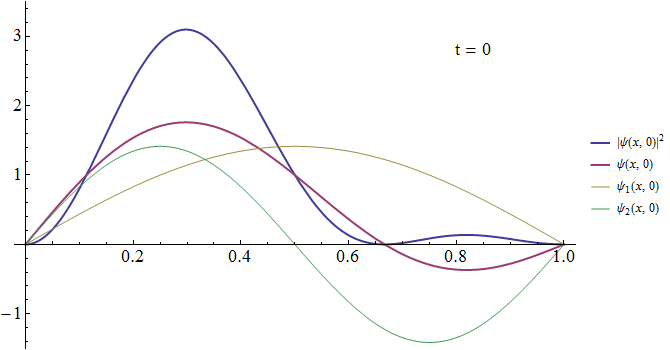
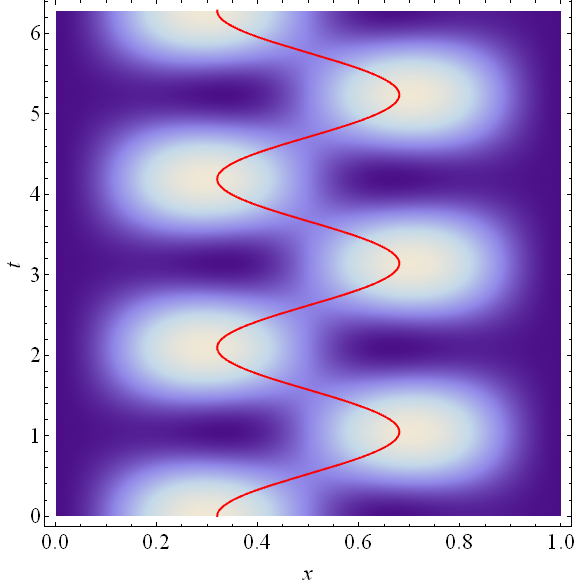
この時間変化をグラフに示せば次のようになる。 $\psi_1$ も $\psi_2$ もその絶対値を変化させないまま複素空間での位相を回転させるが、 その回転速度は後者が前者の4倍である。 その結果2つの波動関数の相対的な位相が変化し、$|\psi(x,t)|^2$ が左右に振動する。
濃淡図の右は縦軸を時間軸として表示したもので、確率密度を明るさで示した。 赤線は $x$ 座標の期待値を表わす。
$$\overline{x}(t)=\int x |\psi(x,t)|^2dx$$
電子が2つの壁にはね返り、振動する様子が見て取れる。
逆に任意の非定常状態を定常状態の重ね合わせで表せる †
任意の関数はフーリエ級数に展開できることを応用数学で学んだ。
すなわち任意の波動関数のある時刻 $t=t_0$ における空間分布は、
$$\psi(x, t_0)=\sum_{n=1}^\infty c_n \varphi_n(x)$$
と表せる。このときこの波動関数の時間発展は、
$$\begin{aligned} \psi(x, t) &=\sum_{n=1}^\infty c_n \varphi_n(x)e^{-i\varepsilon_n(t-t_0)/\hbar}\\ &=\sum_{n=1}^\infty c_n \psi_n(x,t)e^{i\varepsilon_n t_0/\hbar}\\ \end{aligned} $$
で表せる。このことを以下の3点から理解せよ。
- 時間に依存するシュレーディンガー方程式は
$$ i\hbar\underbrace{\frac{\partial}{\partial t}\psi(x,t)}_\text{波動関数の時間変化}= \underbrace{\left[-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}+V(x)\right]\psi(x,t)}_\text{波動関数自身から求まる値} $$
の形であるから、ある時刻の波動関数が分かればそれ以降の時間発展はシュレーディンガー方程式から一意に定まる。 - 上記の関数は時刻 $t=t_0$ において $\psi(x, t_0)$ に一致する
- シュレーディンガー方程式は線形であるから、解 $\psi_n(x,t)$ の一次結合は同じシュレーディンガー方程式の解になる
定常状態はいつ実現する? †
上のような非定常状態は $t\to\infty$ でも振動を続け、いつまで経っても定常状態には落ち着かない。
実際の系では光子を放出するなどして電子はエネルギーを失い、 基底状態に落ち着く。
そのような過程を記述するには、上で学んだシュレーディンガー方程式に 電子の持つ電荷と、周囲の電磁場との相互作用を入れてやる必要がある。 教科書では「量子力学(II)」の13章で扱われている。
1次元の箱の中の自由粒子(有限ポテンシャル) †
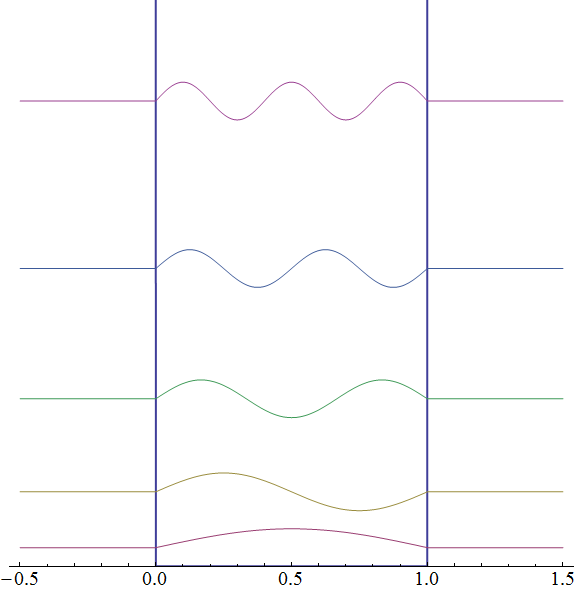
上で求めた解のうち、$n=1\sim 5$ に当たる波動関数をポテンシャル形状と重ねてグラフ化すれば 下左図のようになる。このグラフでは個々の解をエネルギー固有値分だけ上にずらして表示している。 波動関数は箱の内部でのみ有限値を取り、箱の境界および外部ではゼロとなる。
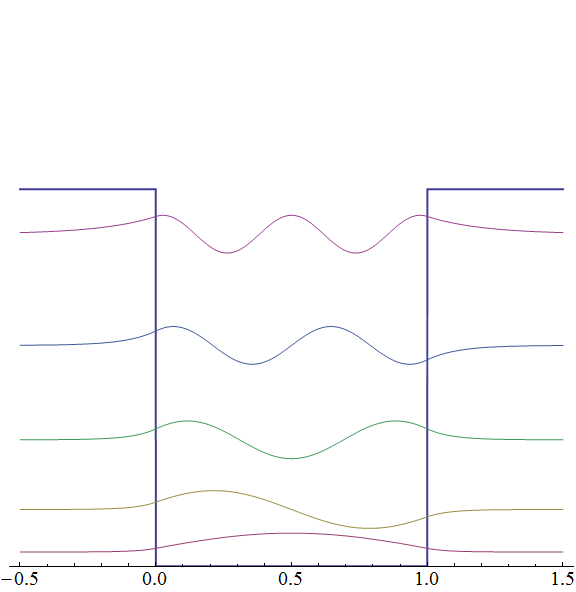
これに対して、有限なポテンシャル障壁 (高さ $V$) によって閉じ込められた自由粒子に対する解は上右図のようになる。それぞれの解は無限大障壁の場合と非常に似通った形をしているが・・・
- 自身のエネルギーよりも高い、障壁の外側部分にまで確率密度が染み出している
- 染み出した分だけ波長が長くなり、すなわち運動量が小さくなり、全エネルギーも低下している
- エネルギーの低い ($n$ の小さい) 解は染み出しが小さいため、無限大障壁の解とほとんど変わらない
特に1番目の特徴について、古典論では自身のエネルギーより高い障壁の外へは一切進入できないのに対して、量子力学では有限エネルギーの障壁で粒子を完全に閉じ込めることができないところに注目せよ。
どうしてこんな解が得られるか †
実は自身のエネルギーよりポテンシャルが大きいような場所では
「運動エネルギーが負になるのだ(なんだって?)」
$$ \underbrace{\varepsilon\phantom p}_\text{全エネルギー}= \underbrace{p^2/2m}_\text{運動エネルギー}+\underbrace{V\phantom p}_\text{ポテンシャル} $$
だから、$\varepsilon<V$ は、$\frac{p^2}{2m}<0$ を表す。 これは $p$ が虚数ならば可能。$p\leftrightarrow \hbar k$ の対応があるため、そこでは波数 $k$ も虚数となる。
以下数式を使って考えよう。
ポテンシャルが一定値 $V(x)=V$ である時、 時間に依存しないシュレーディンガー方程式を変形すれば
$$\left(-\frac{\hbar}{2m}\frac{d^2}{dx^2}+V\right)\varphi=\varepsilon\varphi\hspace{1cm}\text{より}$$
$$\frac{d^2}{dx^2}\varphi=\frac{2m(V-\varepsilon)}{\hbar^2}\varphi$$
を得る。
箱の中のように $\varepsilon>V$ の時、この式は $\varphi''=-k^2\varphi$ の形であるから、
$$\varphi(x)=Ae^{ikx}+Be^{-ikx}\hspace{2cm}(0<x<a)$$
のような振動解が得られる。ただし $k=\sqrt{2m(\varepsilon-V)}/\hbar$
一方、箱の外のように $\varepsilon<V$ の時、この式は $\varphi''=k'^2\varphi$ の形であるから、
$$\varphi(x)=Ce^{k'x}+De^{-k'x}$$
のように、指数関数的な一般解が得られる。ただし、$k'=\sqrt{2m(V-\varepsilon)}/\hbar$。 指数関数は波数が虚数となった振動解と見なせることに注意せよ。
解の接続 †
上のようにいくつかの領域で別々の形の解が得られた場合、 その「接続部分(領域の端)」でも方程式を満たせるようにパラメータを選ぶことで、 「全領域で方程式を満たす解」すなわち「正しい解」を作れる。
シュレーディンガー方程式の性質から次のような接続部の境界条件が要求される。
- 無限遠でゼロになる(束縛されているという条件)
- ポテンシャルエネルギーが有限の不連続性を持つ部分で波動関数が滑らかに繋がる(一次微分まで連続)
証明 → 量子力学Ⅰ/箱の中の自由粒子/メモ#l1fcae51 - ポテンシャルエネルギーに無限大の不連続性がある場合でも波動関数は連続
そこで、
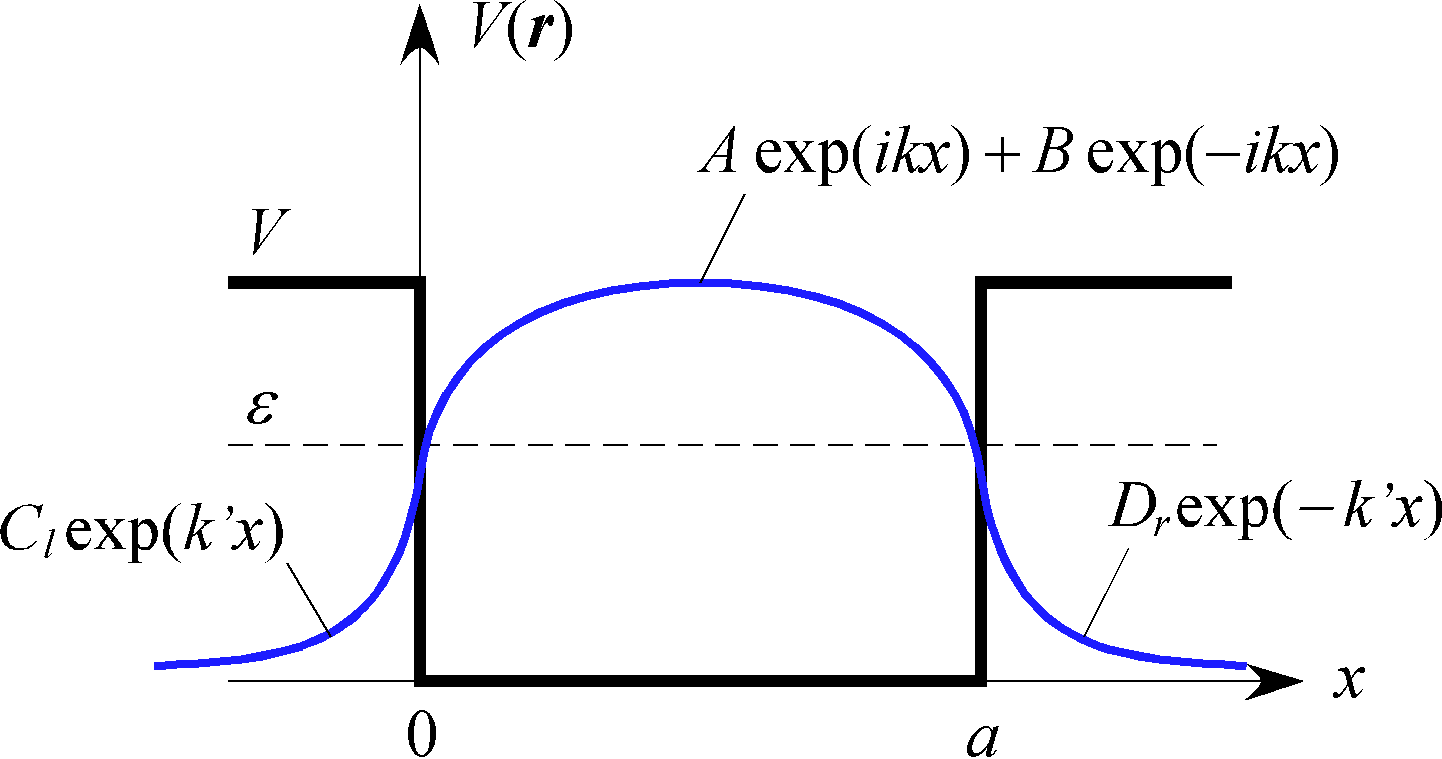
$$ \varphi(x)=\begin{cases} Ce^{k'x}+De^{-k'x}&x<0\\ Ae^{ikx}+Be^{-ikx}&0<x<a\\ C'e^{k'x}+D'e^{-k'x}&a<x\\ \end{cases} $$
と置いて、以下の境界条件からパラメータ $A,B,C,D,C',D',\varepsilon_n$ を決める。
$$\begin{aligned} &\varphi(-\infty)=0,\ \ \varphi(+\infty)=0\ \rightarrow\ D=C'=0\\ &\varphi(-0)=\varphi(+0),\ \ \varphi'(-0)=\varphi'(+0)\\ &\varphi(a-0)=\varphi(a+0),\ \ \varphi'(a-0)=\varphi'(a+0)\\ \end{aligned} $$
$D=C'=0$ より、解の形が「箱の中では振動する」、「箱の外では指数関数的に減衰する」、「境界部分で滑らかに繋がる」形になることがわかる。
式が6つで決めるべきパラメータが7つなので、1つを除いて値が決まる。
ただし、方程式中に周期関数を含むため解は複数存在する。
この決まらずに残る1つのパラメータは波動関数全体にかかる係数である。 そしてその絶対値は「波動関数の規格化」によって決まる。
波動関数の「複素位相」は最後まで決定できないが、 位相は観測可能な物理量ではないため、 位相だけが異なる波動関数は同じ物理状態を表す物として同一視される。 時間に依らない波動関数は常に実数関数として書けることが知られており、 そのように位相を取ることが慣例である。
具体的に計算してみると、境界条件による $k$ への制約は
→ 詳しい導出過程
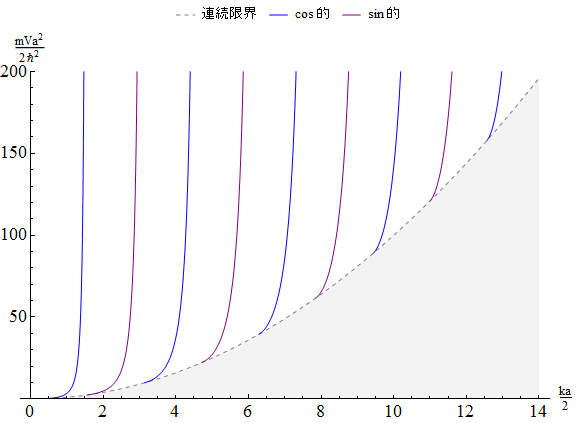
$(ka/2)^2(1+\tan^2(ka/2))=mVa^2/2\hbar$ ただし $\tan(ka/2)>0$
または、
$(ka/2)^2(1+\cot^2(ka/2))=mVa^2/2\hbar$ ただし $\tan(ka/2)<0$
となる。
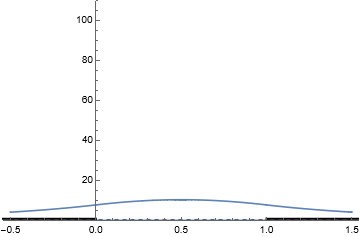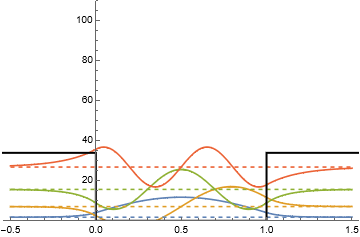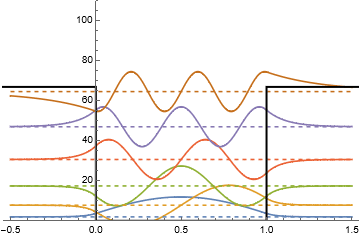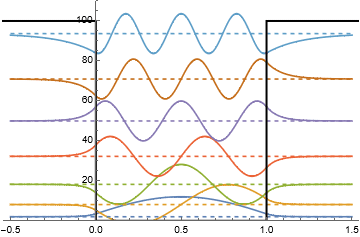
下図に $(ka/2)^2(1+\tan^2(ka/2))$ と $(ka/2)^2(1+\cot^2(ka/2))$ をグラフに表わした。 井戸の幅や深さを $mVa^2/2\hbar$ に代入し、対応する高さに水平線を引いた時、これらの曲線との交点が解を与える。$\tan$ や $\cot$ の周期性を反映して、一般に $k$ についての複数の解が得られることが解る。
グラフの右下の影のかかった部分では $\varepsilon>V$ となり、 このときは箱の外でも振動的な解が得られる。 その場合無限遠における位相に境界条件が課されないため $k$ は 連続値をとれる が、 粒子はポテンシャルに束縛されず無限遠まで広がってしまい、 確率密度として規格化された解を得ることはできない。
縦軸の $mVa^2/2\hbar$ の値によって $ka/2$ には $\varepsilon<V$ の範囲に有限個の解が得られ、それらが離散化した波数、ひいては離散化したエネルギー固有値を与える。 グラフから $V$ が大きくなるほど解の個数が増えていくことが分かる。
$mVa^2/2\hbar\to+\infty$ のときは $ka/2=n\pi/2$ がすべて解になる。 これらの解は $V=+\infty$ の場合に求めた $k_n=\pi/a$ に一致する。
$mVa^2/2\hbar=50$ においては $ka/2$ は $\varepsilon<V$ の範囲に5つの解を持ち、その形状をグラフにしたのが上記の例であった。
上記の計算は例えば金属中に閉じ込められた電子のモデルと考えることができる。 金属中には結晶の周期でイオン核が存在するにも関わらず、 電子は自由に運動できることを固体物理学で学ぶ。 金属中に比べて真空中は電子の感じるエネルギーが高いため、 金属の端面を上で見たポテンシャル障壁と見なすことができる。
ただし金属物体の端面は必ずしも平面的でないし、急峻でもないため、 そのようなポテンシャル形状に対する境界条件は複雑な物になる。 ただ上でも見たとおり、一般に「境界条件」はシュレーディンガー方程式の解を定量的に変えるのみで、 定性的には変化させしない。そこで、不定形の金属の境界条件を箱形であると仮定したり、 あるいは周期的であると仮定したり(箱の一方の端がもう一方と繋がっていることを仮定)して 問題を解いたとしても、端面近傍や極端にエネルギーの高い解の性質を除いて得られる結果は現実の物と 変わらない。そのようにして問題を易しくして解くことが良く行われる。
まとめ †
箱の外で全エネルギーがポテンシャルエネルギーより小さくなる
→ 運動エネルギーが負になる
→ 波数が虚数になる
→ 指数関数的に減衰する
ポテンシャルエネルギーが不連続に変化しても、その変化が有限であれば「波動関数」と「その一次微分」が連続になる
有限の箱型ポテンシャルに束縛された状態は、「波数が実の振動解」と「波数が虚の減衰解」とを箱の境界で「滑らかに接続すること」および「無限遠点での境界条件を満たすこと」によって得られる
そのようにして作った波動関数が、
- それぞれの領域でシュレーディンガー方程式を満たすこと
- 箱の境界における境界条件を満たすこと
- 無限遠点における境界条件を満たすこと
- すなわち「全領域」でシュレーディンガー方程式を満たすこと
に注意せよ
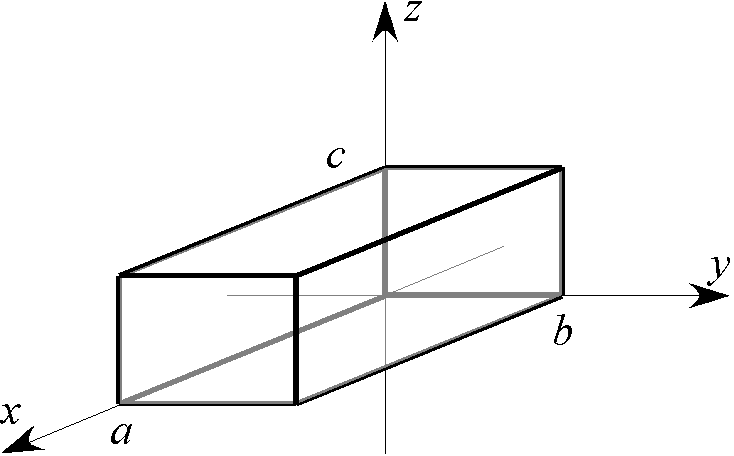
3次元の箱の中の自由粒子 †
$a,b,c$ を正の定数として、$0<x<a$ かつ $0<y<b$ かつ $0<z<c$ の領域に閉じ込められた電子の定常状態を考える。 箱の中ではポテンシャルをゼロ、外ではポテンシャルを無限大とする。
今の場合 $x,y,z$ 座標に相関はないから
$$\varphi(\bm r)=X(x)Y(y)Z(z)$$
のように変数分離できることを仮定して、
$$\begin{aligned} &-\frac{\hbar^2}{2m}\left( \frac{\PD^2}{\PD x^2}+\frac{\PD^2}{\PD y^2}+\frac{\PD^2}{\PD z^2}\right)\Big[X(x)Y(y)Z(z)\Big]\\ &=-\frac{\hbar^2}{2m}\left[ \left(\frac{d^2}{dx^2}X(x)\right)Y(y)Z(z) + X(x)\left(\frac{d^2}{dy^2}Y(y)\right)Z(z) + X(x)Y(y)\left(\frac{d^2}{dz^2}Z(z)\right) \right]\\ &=\varepsilon X(x)Y(y)Z(z) \end{aligned} $$
$$ \left(\frac{d^2}{dx^2}X(x)\right)\frac{1}{X(x)} + \left(\frac{d^2}{dy^2}Y(y)\right)\frac{1}{Y(y)} + \left(\frac{d^2}{dz^2}Z(z)\right)\frac{1}{Z(z)} =\frac{-2m\varepsilon}{\hbar^2} $$
左辺の各項はそれぞれ $x,y,z$ のみの関数であり、右辺は定数である。 任意の $x,y,z$ に対してこの式が成り立つためには、左辺の各項が定数でなければならない。
すなわち、
$$\begin{aligned} &\left(\frac{d^2}{dx^2}X(x)\right)\frac{1}{X(x)} = \frac{-2m\varepsilon_x}{\hbar^2}\\ &\left(\frac{d^2}{dy^2}Y(y)\right)\frac{1}{Y(y)} = \frac{-2m\varepsilon_y}{\hbar^2}\\ &\left(\frac{d^2}{dz^2}Z(z)\right)\frac{1}{Z(z)} = \frac{-2m\varepsilon_z}{\hbar^2}\\ &\varepsilon_x+\varepsilon_y+\varepsilon_z=\varepsilon \end{aligned} $$
$X(x),Y(y),Z(z)$ に対する方程式は1次元の箱形ポテンシャルの問題に帰着して、
$$X_{n_x}(x)=\sqrt{\frac{2}{a}}\sin\left(\frac{n_x\pi}{a} x\right)$$
$$\varepsilon_{x,n_x}=\frac{\hbar^2 \pi^2}{2ma^2}n_x^2$$
等の解を得る。$\varphi(\bm r)$ の解は量子数 $n_x,n_y,n_z$ により指定できて、
$$\varphi_{n_x,n_y,n_z}(\bm r)=\sqrt{\frac{8}{abc}}\sin(n_x\pi x/a)\sin(n_y\pi y/b)\sin(n_z\pi z/c)$$
$$\varepsilon_{n_x,n_y,n_z}=\frac{\hbar^2 \pi^2}{2m}(n_x^2/a^2+n_y^2/b^2+n_z^2/c^2)$$
となる。
例えば電子($m=9.11\times 10^{-31}\,\mathrm{kg}$) を $a=b=c=1\,\mathrm{nm}$ に閉じ込めれば、ゼロ点エネルギーは $11.3\,\mathrm{eV}$ となる。
次の準位は $\varepsilon_{211}=\varepsilon_{121}=\varepsilon_{112}=22.6\,\mathrm{eV}$ である。
このように異なる量子数に対応する波動関数のエネルギーが等しいとき、 それらの準位は縮退していると言う。この様子を示したのが下図左である。
$a=b\ne c$ では $x,y,z$ 方向の対称性が崩れるため、 このうちいくつかの縮退が解けて、準位の分裂が生じる。 $a=b=c/1.1$ としたときのエネルギー準位と、分裂前の縮退した準位との関係を下図右に示した。
まとめ †
水素原子中の電子のエネルギーレベルを正しく再現するなど、 シュレーディンガー方程式が正しそうなことが分かったことから、 同方程式により記述される量子力学的現象を理解するために 簡単な問題を解いてみた。
「量子力学的現象」には我々の直感が働かないため、 今後も同様に、シュレーディンガー方程式を調べることで、 量子力学的現象に対する直感を養うという手順で量子力学を学んでいく。
今回見た下記の特徴は定常状態を扱う他の問題でも同様に現れるため良く理解しておくこと。
- 「井戸の中」のように $\varepsilon>V(x)$ となる領域では波動関数は振動する
- 「壁に染み出した部分」のように $\varepsilon<V(x)$ となる領域では、指数関数的に減衰する
- 定常状態の空間部分 $\varphi(\bm r)$ は実数関数として書き表せる*3定常状態 $\varphi(\bm r)$ を実数関数として書き表せる証明は 量子力学Ⅰ/箱の中の自由粒子/メモ#t5b8d7c3(https://dora.bk.tsukuba.ac.jp:...)
- 時間的には $e^{-i\varepsilon t/\hbar}$ で位相が回転する
- 1次元の解は縮退しないが*41次元の解は縮退しないことの証明は 量子力学Ⅰ/箱の中の自由粒子/メモ#e976c7dd(https://dora.bk.tsukuba.ac.jp:...)、3次元の解は空間に等方性があればそれに応じて縮退する
- 定常状態の基底状態でさえも運動エネルギーはゼロにならない
- 基底状態・励起状態とも、狭い領域に閉じ込めることで運動エネルギーが上昇する
質問・コメント †
無限高さの箱の中の自由粒子の運動量の記述 †
morimoto hideo? ()
無限高さの箱の中の自由粒子ですが(無限深さの井戸でも)
運動量を測定すれば、それぞれ 1/2の確率で
+nπh'/a または −nπh'/a のどちらかの値が得られる
という記述は間違いと思います。
根拠は
「無限高さの箱」の場合、
p=-ih'∂x は、エルミート演算子ですが
自己共役演算子にはなりません。
したがって、固有値は意味を持ちません
1.田崎晴明 @Hal_Tasaki :
https://www.gakushuin.ac.jp/~881791/d/1506.html#17
2.岩波講座・現代物理学の基礎「量子力学 II」新装版
江沢先生のパートに該当の内容が入っているようです(田崎先生による)
- ご指摘ありがとうございます、修正が必要ですね。検討いたします。 -- 武内(管理人)?
- こちらこそ、ありがとうございます。尚、この「無限高さの箱の運動量」の問題は、 ほぼ10年、EMANの掲示板で議論が続いたものです。 解決に導いて頂いたのは、東北大の堀田先生です。 -- morimoto?
- いただいたご指摘を元に本文を修正いたしました。系を $x\in[0,a]$ に閉じたものと考えず、あくまで $x\in(-\infty,\infty)$ の範囲で考える限り、恐らく「微分不可能な点」があることを除いてこの授業で扱う枠組みで説明可能であると考えました。「微分不可能な点」については本来慎重な扱いが必要になりますが、この問題を「有限な井戸」の極限として考える限り、$p$ や $p^2$ の期待値を求める上で影響はないと考えました。 -- 武内(管理人)?
教科書について †
タカギ タイセイ? ()
他大学の者です。
教科書は何を使っていますか?
- 教科書には 小出昭一郎 著 「量子力学 (I)」 を指定しています。 -- 武内(管理人)?
- 初歩的な質問で申し訳ありません。 -- ナカタ?
- 波数が虚数とありますが、運動エネルギーでなくk´から考えると正の数で実数に見えるのですが、k´と運動エネルギーの波数kは別なのでしょうか -- ナカタ?
- 他の方の質問欄に質問してしまいました。申し訳ありません。 -- ナカタ?
固定端条件と周期的境界条件 †
()
箱の中の自由粒子について議論するときに、境界条件として、i)固定端条件やii)周期的境界条件を課すことがあると思います。(本文中では、固定端条件を用いていると思います。)
これらの境界条件はどのように使い分けているのですか?
- 固定端条件に対するエネルギー固有関数は運動量の固有関数にはならず、上記の通り実数関数として表せることから運動量の期待値はゼロになります。一方、周期的境界条件を用いるとエネルギーと運動量の同時固有関数を作れます。ですので運動量空間(波数空間)で話をしたい場合には周期的境界条件を仮定することになるのだと思います。 -- 武内(管理人)?
アニメーションの作り方について †
neko? ()
コメントの位置間違えました。
「非定常状態の解」のセクションにあるアニメーションですが、どのように作成しましたか?また、用いたプログラミング言語も教えてください。
- こちらに公開しています → 量子力学Ⅰ/箱の中の自由粒子/メモ#n62d71f3。 他のページのグラフ等も「メモ」に置いてあることが多いです。 -- 武内(管理人)?
- 回答ありがとうございます。調べてみます。 -- neko?
「逆に任意の非定常状態を定常状態の重ね合わせで表せる」の項について †
匿名希望? ()
第二式目はψ(x,t=0)についての式でなく、ψ(x,t)についての式なのではないでしょうか?
また、第二式目のexpの指数はε1でなく、εnでないでしょうか?
- ありがとうございます、ご指摘の通りでした。本文を修正いたしました。 -- 武内(管理人)?
作り方 †
あ? ()
このグラフの作り方を教えてください
*1 通常は $\varphi$ の1次微分 $d\varphi/dx$ も連続となるが、ここではポテンシャルの無限大の不連続性を反映して微係数は不連続になる
*2 2つの直交するベクトルを加えて規格化する際の係数が $1/\sqrt 2$ であったことを思い出そう
*3 定常状態 $\varphi(\bm r)$ を実数関数として書き表せる証明は 量子力学Ⅰ/箱の中の自由粒子/メモ#t5b8d7c3
*4 1次元の解は縮退しないことの証明は 量子力学Ⅰ/箱の中の自由粒子/メモ#e976c7dd
添付ファイル: