エネルギー保存・運動量保存
目次 †
点電荷の系 †
電磁ポテンシャルの導入 では、 $\bm i(\bm x,t),\rho(\bm x,t)$ を与えて、そこから生まれる $\bm E(\bm x,t),\bm B(\bm x,t)$ を求める問題について考えた。
ここでは、$\bm E(\bm x,t),\bm B(\bm x,t)$ ばかりでなく $\bm i(\bm x,t),\rho(\bm x,t)$ も未知であり 電荷が電磁場と相互作用しながら共に時間発展していく様子を記述することを考える。
系は $n$ 個の点電荷からなり、$k$ 番目の電荷は
- 電荷 $e_k$
- 質量 $m_k$
- 位置座標 $\bm z_k(t)$
を持つとする。
電荷密度 †
1つの点電荷 $e$ が作る電荷密度を考えよう。
$\bm x=\bm z(t)$ に電荷があり、 それ以外で電荷密度はゼロであるから、 電荷密度は Dirac のデルタ関数を用いて、
$$\begin{aligned}\rho(\bm x,t)=e\delta^3(\bm x-\bm z(t))\end{aligned}$$
と表せる。この式から時間と共に点電荷が移動し、 電荷密度が変化する様子を思い浮かべられるだろうか?
ここで、$\delta^3(\bm x)=\delta(x)\delta(y)\delta(z)$ であり、 Dirac のデルタ関数 $\delta(x)$ は
$$\begin{aligned}\delta(x)=\begin{cases}0&x\ne 0\\+\infty&x=0\end{cases}\end{aligned}$$
$$\begin{aligned}\delta(-x)=\delta(x)\end{aligned}$$
$$\begin{aligned}\int_{-\infty}^\infty\delta(x)dx=1\end{aligned}$$
を満たす。
電流密度 †
点電荷 $e$ の電流密度は次のように書ける。
$$\begin{aligned}\bm i(\bm x,t)=e\dot{\bm z}(t)\delta^3(\bm x-\bm z(t))\end{aligned}$$
と言われても、
- 電流密度が点電荷の存在する位置 $\bm z(t)$ 以外でゼロになること、
- 大きさが電荷 $e$ およびその速度 $\dot{\bm z}(t)$ に比例すること、
は納得できるとして、
- 他に係数が必要ないのか?
と、心配になるかもしれない。
この点は、電荷保存則が成り立っていることを確認すれば納得できる。
$$\begin{aligned} \frac{\partial}{\partial t}\rho(\bm x,t) &=-e\dot{\bm z}(t)\cdot\grad\delta^3(\bm x-\bm z(t))\\ &=-e\sum_{a=x,y,z}\dot z_a(t)\frac{\partial}{\partial a}\delta^3(\bm x-\bm z(t)) \end{aligned}$$
$$\begin{aligned} \DIV \bm i(\bm x,t) &=e\,\DIV\{\dot{\bm z}(t)\delta^3(\bm x-\bm z(t))\}\\ &=e\sum_{a=x,y,z}\frac{\partial}{\partial a}\dot z_a(t)\delta^3(\bm x-\bm z(t))\\ &=e\sum_{a=x,y,z}\dot z_a(t)\frac{\partial}{\partial a}\delta^3(\bm x-\bm z(t)) \end{aligned}$$
$$\begin{aligned} \therefore \frac{\partial}{\partial t}\rho(\bm x,t)+\DIV \bm i(\bm x,t)=0 \end{aligned}$$
として、上記の電流密度の式が正しいことが分かる。
Lorentz力 †
点電荷 $e$ に働く力は、
$$\begin{aligned} \bm f(t)&=m\ddot{\bm z}(t)\\ &=\int\Big[\rho(\bm x,t)\bm E(\bm x,t)+\bm i(\bm x,t)\times\bm B(\bm x,t)\Big]d^3x\\ &=\int\Big[e\delta^3(\bm x-\bm z(t))\bm E(\bm x,t)+e\delta^3(\bm x-\bm z(t))\dot{\bm z}(t)\times\bm B(\bm x,t)\Big]d^3x\\ &=e\bm E(\bm z(t),t)+e\dot{\bm z}(t)\times\bm B(\bm z(t),t) \end{aligned}$$
と表せる。
解くべき方程式 †
以上を合わせると、
- 運動方程式
- 電荷密度、電流密度
- Maxwell 方程式
をすべて連立させることで、系の時間発展を記述できる。
$$\begin{aligned} \left\{\begin{array}{l} m_1\ddot{\bm z}_1(t)=e_1\Big[\bm E(\bm z_1(t),t)+\dot{\bm z}_1(t)\times\bm B(\bm z_1(t),t)\Big]\\[2mm] m_2\ddot{\bm z}_2(t)=e_2\Big[\bm E(\bm z_2(t),t)+\dot{\bm z}_2(t)\times\bm B(\bm z_2(t),t)\Big]\\[2mm] m_3\ddot{\bm z}_3(t)=e_3\Big[\bm E(\bm z_3(t),t)+\dot{\bm z}_3(t)\times\bm B(\bm z_3(t),t)\Big]\\ \vdots\\ \displaystyle\rho(\bm x,t)=\sum_{k=1}^n e_k\delta^3(\bm x-\bm z_k(t))\\[2mm] \displaystyle\bm i(\bm x,t)=\sum_{k=1}^n e_k\dot{\bm z}_k(t)\delta^3(\bm x-\bm z_k(t))\\[2mm] \displaystyle\rot\bm E(\bm x,t)+\frac{\partial}{\partial t}\bm B(\bm x,t)=\bm 0\\[2mm] \displaystyle\DIV\bm B(\bm x,t)=0\\[2mm] \displaystyle\frac{1}{\mu_0}\rot \bm B(\bm x,t)-\varepsilon_0\frac{\partial}{\partial t}\bm E(\bm x,t)=\bm i(\bm x,t)\\[3mm] \displaystyle\varepsilon_0\DIV\bm E(\bm x,t)=\rho(\bm x,t)\\ \end{array}\right. \end{aligned}$$
以下ではこの方程式で記述される系の物理的性質を調べ、 電磁場の持つエネルギーや運動量について学ぶ。
Galilei の相対性について †
ある質点の運動 $\bm z(t)$ は、速度 $\bm v$ で動く人から見ると
$$ \bm z'(t)=\bm z(t)-\bm vt $$
のように観測される。このとき、
$$ \dot{\bm z}'(t)=\dot{\bm z}(t)-\bm v $$
$$ \ddot{\bm z}'(t)=\ddot{\bm z}(t) $$
であるから、
$$ \bm f(t)=m\ddot{\bm z}(t)=m\ddot{\bm z}'(t) $$
のように、静止した人に対しても、等速直線運動する人に対しても同様に成り立つ。
このことをGalileiの相対性と呼ぶ。
→ 絶対的な静止系は存在せず、静止・運動は相対的であるということ
Maxwell の方程式に対して同様の相対性が成り立つだろうか?
ある座標で見て電荷が一点で静止していれば、その周りには球対称な電場のみが存在する。
同じ状況を等速直線運動する人から見れば、 電荷は移動しており、その周りには電場だけではなく磁場も発生しているはずである。
このことは、磁場の大きさ・方向、あるいは有無自体が観測者の運動に依存することを 示しており、直感的な意味での Galilei の相対性が失われていることを示している。
このあたりをしっかり考えていくことで、
エネルギー保存則 †
遠隔相互作用では:
- 静電ポテンシャル $\displaystyle\frac{1}{4\pi\varepsilon_0}\frac{e_1e_2}{r^2}$
- コイルの電流 $\displaystyle\frac{L}{2}I^2$
- コンデンサの電荷 $\displaystyle\frac{Q^2}{2C}$
- ジュール熱 $\displaystyle\int_0^\infty IV\,dt$
- 光の運ぶエネルギー $\text{(太陽定数)}=1,366\,\mathrm{W/m}^2$
というように、個々の問題に対して別々の方法でエネルギーを測っていた。
近接相互作用の考え方で:
- 電磁場の存在する空間の持つエネルギー
- 電磁場により運ばれるエネルギー
を、局所的な電磁場の値のみによって定義しようというのが以下の目標である。
これらは同じエネルギーを別の形で表わそうというものなので、 ある意味排他的である。すなわち、遠隔相互作用的なエネルギーと、 近接相互作用的なエネルギーの両方でエネルギーを記述してしまうと、 同じエネルギーを2度測ってしまうことになるため注意せよ。
基本 †
エネルギー保存則を式で書けば:
$$\begin{aligned}\frac{d}{dt}(エネルギー)=0\end{aligned}$$
あるいは、
$$\begin{aligned}\frac{d}{dt}(エネルギー)=(単位時間あたりに入ってくるエネルギー)\end{aligned}$$
となるはず。
一般に、このような式は Newton 方程式に速度を掛けることで得られる。
$$\begin{aligned} &\bm f=m\ddot{\bm z}\\ &\bm f\cdot\dot{\bm z}=m\ddot{\bm z}\cdot\dot{\bm z}= \frac{d}{dt}\Big(\frac{1}{2}m|\dot{\bm z}|^2\Big)\\ \end{aligned}$$
この左辺 $\bm f\cdot\dot{\bm z}$ は系に「加えられる単位時間当たりの仕事」を表わし、
右辺は運動エネルギー $\frac{1}{2}m|\dot{\bm z}|^2$ の単位時間当たりの増加量を表わす。
Lorentz 力に適用する †
$$\begin{aligned} &m_k\dot{\bm z}_k(t)\cdot\ddot{\bm z}_k(t)\\ &=\frac{d}{dt}\Big(\frac{1}{2}m_k|\dot{\bm z}_k(t)|^2\Big)\\ &=e_k\dot{\bm z}_k(t)\cdot\bm E(\bm z_k(t),t)+e_k\underbrace{\dot{\bm z}_k(t)\cdot\big[\dot{\bm z}_k(t)\times\bm B(\bm z_k(t),t)\big]}_{\displaystyle \bm a\cdot(\bm a\times\bm b) の形なのでゼロ} \end{aligned}$$
すべての粒子について足し合わせると、
$$\begin{aligned} &\frac{d}{dt}\left(\sum_{k=1}^n\frac{1}{2}m_k|\dot{\bm z}_k(t)|^2\right)\\ &=\sum_{k=1}^n e_k\dot{\bm z}_k(t)\cdot\bm E(\bm z_k(t),t)\\ &=\sum_{k=1}^ne_k\dot{\bm z}_k(t)\cdot\int d^3x\ \delta^3(\bm x-\bm z_k(t))\bm E(\bm x,t)\\ &=\int d^3x\ \left(\sum_{k=1}^ne_k\dot{\bm z}_k(t)\delta^3(\bm x-\bm z_k(t))\right)\cdot\bm E(\bm x,t)\\ &=\int d^3x\ \bm i(\bm x,t)\cdot\bm E(\bm x,t) \end{aligned}$$
Maxwell 方程式を用いて $\bm i(\bm x,t)$ を書き直すと、
$$\begin{aligned} &=\int d^3x\ \left(\frac{1}{\mu_0}\rot B-\varepsilon_0\frac{\partial\bm E}{\partial t}\right)\cdot\bm E(\bm x,t)\\ \end{aligned}$$
Maxwell 方程式より $\rule[0pt]{0pt}{32pt}\frac{1}{\mu_0}\bm B\cdot\underbrace{\left(\frac{\partial\bm B}{\partial t}+\rot\bm E\right)}_{=\bm 0}=0$ を加えると、
$$\begin{aligned} &=\int d^3x\ \left[\frac{1}{\mu_0}\rot\bm B\cdot\bm E-\frac{1}{\mu_0}\bm B\cdot\rot\bm E-\frac{1}{\mu_0}\bm B\cdot\frac{\partial\bm B}{\partial t}-\varepsilon_0\bm E\cdot\frac{\partial\bm E}{\partial t}\right]\\ \end{aligned}$$
ベクトル解析の公式から、$\DIV(\bm E\times\bm B)=\bm B\cdot\rot\bm E-\bm E\cdot\rot\bm B$ なので、
$$\begin{aligned} &=\int d^3x\ \left[- \frac{1}{\mu_0}\DIV(\bm E\times\bm B)- \frac{\partial}{\partial t}\left\{\frac{1}{2\mu_0}|\bm B|^2-\frac{\varepsilon_0}{2}|\bm E|^2\right\}\right]\\ &=-\int_S \underbrace{\frac{1}{\mu_0}(\bm E\times\bm B)}_{=\,\bm S(\bm x,t)}\cdot\bm ndS- \frac{d}{dt}\int d^3x\ \underbrace{\left\{\frac{1}{2\mu_0}|\bm B|^2-\frac{\varepsilon_0}2|\bm E|^2\right\}}_{=\,w(\bm x,t)}\\ \end{aligned}$$
エネルギー保存の式 †
結果として、
$$\begin{aligned} \frac{d}{dt}\Bigg[\underbrace{\sum_{k=1}^n\frac{1}{2}m_k|\dot{\bm z}_k(t)|^2}_\text{全質点の運動エネルギー}+\underbrace{\rule[-2.8ex]{0pt}{1ex}\int d^3x\,w(\bm x,t)}_\text{電磁場のエネルギー}\Bigg]= \underbrace{\rule[-2.8ex]{0pt}{0pt}-\int_S\bm S(\bm x,t)\cdot\bm n\,dS}_\text{界面から入ってくる量} \end{aligned}$$
の形を得る。
ここで、
- 電磁場のエネルギー密度
$$\begin{aligned} w(\bm x,t)&=\frac{\varepsilon_0}2|\bm E|^2+\frac{1}{2\mu_0}|\bm B|^2 \end{aligned}$$ - 電磁場によるエネルギー流量 (
Poynting ベクトル)
$$\begin{aligned} \bm S(\bm x,t)&=\frac{1}{\mu_0}\bm E\times\bm B \end{aligned}$$
と考えれば、上記の結果を以下のように理解できる。
- 電場 $\bm E$ あるいは磁場 $\bm B$ が存在する空間は、 電場・磁場の2乗に比例する密度でエネルギーを蓄えていること
- 電場 $\bm E$ と磁場 $\bm B$ とが同時に存在し、なおかつ非平行な場合、 空間に蓄えられたエネルギーは単位時間・単位面積あたり $\bm S$ の流れを持つこと
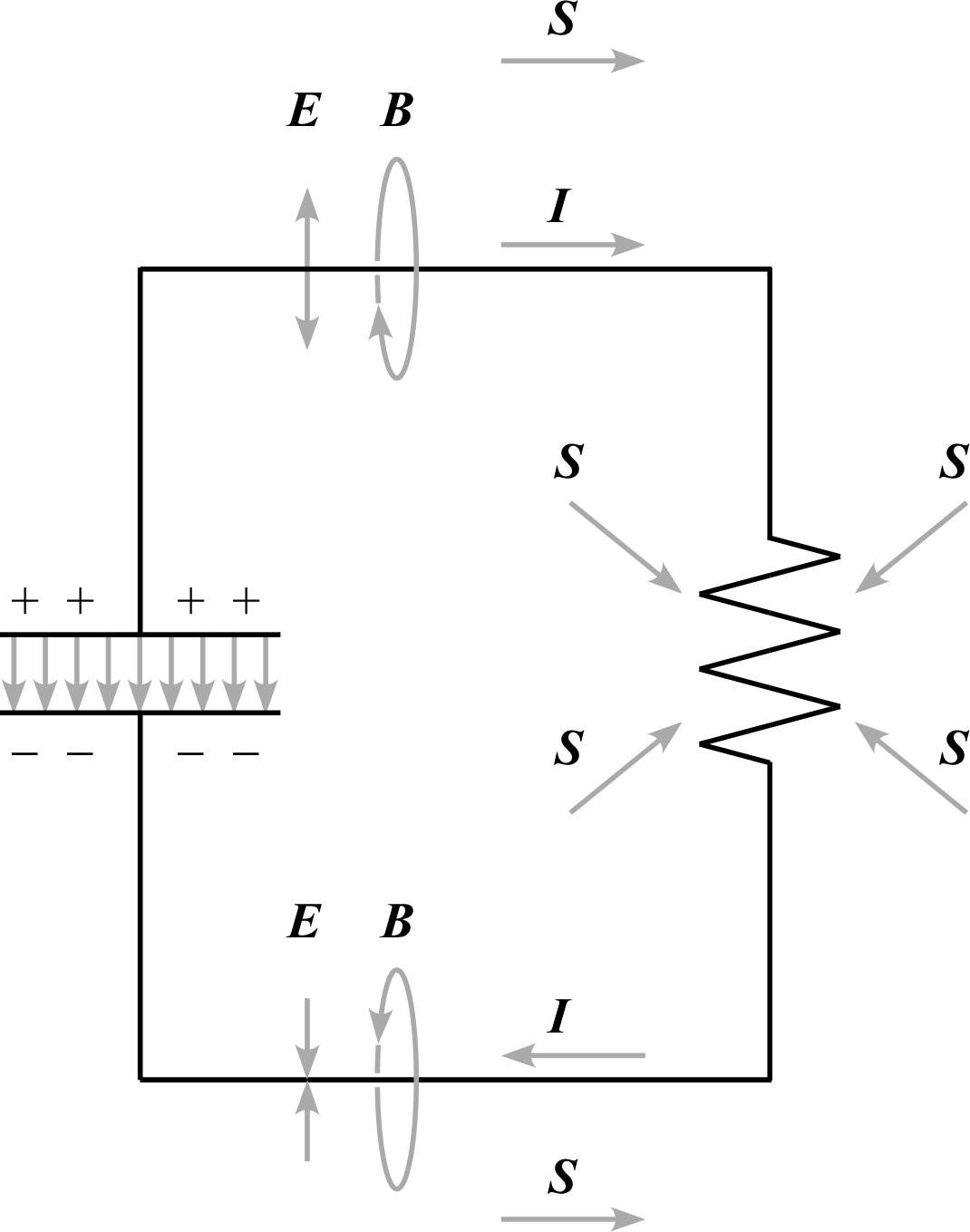
例:コンデンサの放電 †
回路学ではコンデンサに蓄えられたエネルギーを $\displaystyle\frac{Q^2}{2C}=\frac{CV^2}{2}$ などと表わすが、近接相互作用の考えでは「電場の存在する空間」がそのエネルギーを蓄えていると考える。
具体的にはコンデンサを構成する平板電極間の電場の強い領域にわたって、上記 $w(\bm x,t)$ を積分することにより蓄えられたエネルギーを求められる(当然その値は $\displaystyle\frac{Q^2}{2C}=\frac{CV^2}{2}$ と等しくなる)。
回路学では電圧 $V$ で電流 $I$ が流れるとき、電力(仕事量)$IV$ が運ばれるが、近接相互作用の考えでは導線を流れる電流そのものではなく その周りに生じる電場・磁場がエネルギーを運ぶ。
図の上部では導線は周囲に比べて高電位であるから、電場は導線を中心に外向きである。 また、電流は右向きに流れるため、磁場は図の向きで導線を取り囲む。 その結果、Poynting ベクトル $\bm S$ は右向きとなり、 コンデンサから抵抗へエネルギーを運ぶ。
図の下部では導線は周囲に比べて低電位であるから、電場は導線を中心に内向きである。 また、電流は左向きに流れるため、磁場は図の向きで導線を取り囲む。 その結果、Poynting ベクトル $\bm S$ はやはり右向きとなり、 コンデンサから抵抗へエネルギーを運ぶ。
Poynting ベクトルは全体を通じてコンデンサから湧き出し抵抗器へ吸い込まれることになり、 その結果、コンデンサのエネルギーが抵抗器にてジュール熱として失われる。
回路学に代表される遠隔相互作用の視点と、 上記のような近接相互作用的な視点とは同じものを異なる見方をしたものであり、 表裏一体の関係にある。2つの見方をしっかりと対比させて理解せよ。
運動量保存則 †
光が運動量を運ぶことは有名であり、これを利用した光子ヨットなども検討されている。*1以前は「ラジオメーター」(https://www.google.com/search?...) により光の運動量を目で見ることができると記述していたのですが、これは誤りとのこと。https://ja.wikipedia.org/wiki/ラジオメーター効果#誤った原理説明(https://ja.wikipedia.org/wiki/...) すみませんでした。
すなわち、電磁場はそれ自体が運動量を持ち、その値は物質系や外界との相互作用で刻々と変化する。
そこで、
(系の全運動量)=(質点系の運動量)+(電磁場の運動量)
と考え、全運動量の時間変化について考えることにしよう。
基本 †
Newton 方程式を
$$\begin{aligned}\bm f=m\ddot{\bm z}=\frac{d}{dt}\underbrace{\Big(\,m\dot{\bm z}\,\Big)}_\text{運動量}\end{aligned}$$
のように変形すると、 運動量の時間変化は外力に等しいことを示している。
Lorentz力の式から、系の全運動量の時間変化を考えよう。
$$\begin{aligned} &\sum_{k}m_k\ddot{\bm z}_k(t)=\frac{d}{dt}\Big(\sum_km_k\dot{\bm z}_k(t)\Big)\\ &=\sum_k \Big[e_k\bm E(\bm z_k,t)+e_k\dot{\bm z}_k(t)\times\bm B(\bm z_k,t)\Big]\\ &=\sum_k\int d^3x \Big[e_k\delta(\bm x-\bm z_k(t))\bm E(\bm x,t)+e_k\dot{\bm z}_k(t)\times\delta(\bm x-\bm z_k(t))\bm B(\bm x,t)\Big]\\ &=\int d^3x \Big[\Big\{\sum_ke_k\delta(\bm x-\bm z_k(t))\Big\}\bm E(\bm x,t)+\Big\{\sum_ke_k\dot{\bm z}_k(t)\delta(\bm x-\bm z_k(t))\Big\}\times\bm B(\bm x,t)\Big]\\ &=\int d^3x \Big[\rho(\bm x,t)\bm E(\bm x,t)+\bm i(\bm x,t)\times\bm B(\bm x,t)\Big]\\ \end{aligned}$$
Maxwell 方程式を用いて $\rho,\bm i$ を書き換えると、
$$\begin{aligned} &=\int d^3x \Big[\Big(\varepsilon_0\DIV \bm E\Big)\bm E+\Big(\frac{1}{\mu_0}\rot\bm B-\varepsilon_0\frac{\partial \bm E}{\partial t}\Big)\times\bm B\Big]\\ \end{aligned}$$
さらに、
$$\begin{aligned} \frac{\partial}{\partial t}\Big(\varepsilon_0\bm E\times\bm B\Big) &=\varepsilon_0\frac{\partial\bm E}{\partial t}\times \bm B+\varepsilon_0\bm E\times\frac{\partial\bm B}{\partial t}\\ &=\varepsilon_0\frac{\partial\bm E}{\partial t}\times \bm B-\varepsilon_0\bm E\times\rot \bm E\\ \end{aligned}$$
を積分して両辺に加えれば、
$$\begin{aligned} &\frac{d}{dt}\Big[ \underbrace{\sum_km_k\dot{\bm z}_k(t)}_\text{全質点の運動量}+ \underbrace{\frac{1}{c^2}\rule[-3ex]{0pt}{1ex}}_{\displaystyle\varepsilon_0\mu_0}\int d^3x \underbrace{\rule[-3ex]{0pt}{1ex}\Big(\frac{1}{\mu_0}\bm E\times\bm B\Big)}_{\displaystyle \bm S}\Big]\\ &=\int d^3x\ \Big[\varepsilon_0(\DIV \bm E)\bm E+\varepsilon_0(\rot \bm E)\times\bm E+\\ &\hspace{18mm}\underbrace{\frac{1}{\mu_0}(\DIV \bm B)\bm B}_{\displaystyle=0}+ \frac{1}{\mu_0}(\rot \bm B)\times\bm B\Big] \end{aligned}$$
を得る。ただし、式の対称性を高めるために常にゼロとなる項 $\frac{1}{\mu_0}(\DIV \bm B)\bm B$ を右辺に加えた。
右辺は対称性は良いものの、まだごちゃごちゃしていて分かりづらい。ここを何とかしよう。
$(\mathrm{div}\,\bm X)\bm X+(\mathrm{rot}\,\bm X)\times\bm X$ という量について †
次のような2階のテンソル量を考える。
(2階のテンソルは行列(ベクトルに対する線形写像)の形で表される物理量のこと、1階のテンソルはベクトルとして表される物理量のこと。どちらも座標変換に対して決まった法則に従い形を変える。)
$$\begin{aligned} T^e&=\varepsilon_0\begin{pmatrix} E_x^2-\frac{1}{2}|\bm E|^2&E_xE_y&E_xE_z\\ E_yE_x&E_y^2-\frac{1}{2}|\bm E|^2&E_yE_z\\ E_zE_x&E_zE_y&E_z^2-\frac{1}{2}|\bm E|^2\\ \end{pmatrix}\\ &=\varepsilon_0\begin{pmatrix} E_x^2&E_xE_y&E_xE_z\\ E_yE_x&E_y^2&E_yE_z\\ E_zE_x&E_zE_y&E_z^2\\ \end{pmatrix}-\frac{\varepsilon_0}{2}|\bm E|^2I\\ &=\varepsilon_0\Big[ \begin{pmatrix}E_x\\E_y\\E_z\end{pmatrix} \begin{pmatrix}E_x&E_y&E_z\end{pmatrix}-\frac{1}{2}\begin{pmatrix}E_x&E_y&E_z\end{pmatrix}\begin{pmatrix}E_x\\E_y\\E_z\end{pmatrix}I\Big]\\ &=\varepsilon_0\Big[\bm E\bm E^T-\frac{1}{2}(\bm E^T\bm E) I\Big]\\ \end{aligned}$$
直交行列 $R$ により $\bm E\to \bm E'=R\bm E$ の形の座標変換が施されるとき、 $T^e$ の変換規則は次のようになり、この量が2階のテンソル量であることを確認できる。
$$\begin{aligned} T^e\to {T^e}'&=\varepsilon_0\Big[(R\bm E)(R\bm E)^T-\frac{1}{2}\{(R\bm E)^T(R\bm E)\} I\Big]\\ &=\varepsilon_0\Big[R\bm E\bm E^TR^T-\frac{1}{2}(\bm E^T\underbrace{R^TR}_{=I}\bm E) \underbrace{R^TR}_{=I}\Big]\\ &=\varepsilon_0R\Big[\bm E\bm E^T-\frac{1}{2}(\bm E^T\bm E) I\Big]R^T\\ &=R\,T^eR^T\\ \end{aligned}$$
これは典型的な2階のテンソル量の座標変換である。
この $T^e$ に対して、
$$\begin{aligned}\DIV \bm E=\begin{pmatrix}\frac{\partial}{\partial x}&\frac{\partial}{\partial y}&\frac{\partial}{\partial z}\end{pmatrix} \begin{pmatrix}E_x\\E_y\\E_z\end{pmatrix}\end{aligned}$$
であったのと同様に、
$$\begin{aligned} \DIV T^e &=\begin{pmatrix}\frac{\partial}{\partial x}&\frac{\partial}{\partial y}&\frac{\partial}{\partial z}\end{pmatrix} \begin{pmatrix}T^e_{xx}&&T^e_{xy}&&T^e_{xz}\\T^e_{yx}&&T^e_{yy}&&T^e_{yz}\\T^e_{zx}&&T^e_{zy}&&T^e_{zz}\\\end{pmatrix}\\ &=\begin{pmatrix}\rule[-4ex]{0pt}{9ex} \big(\frac{\partial T^e_{xx}}{\partial x}+\frac{\partial T^e_{yx}}{\partial y}+\frac{\partial T^e_{zx}}{\partial z}\big)& \big(\frac{\partial T^e_{xx}}{\partial x}+\frac{\partial T^e_{yx}}{\partial y}+\frac{\partial T^e_{zx}}{\partial z}\big)& \big(\frac{\partial T^e_{xx}}{\partial x}+\frac{\partial T^e_{yx}}{\partial y}+\frac{\partial T^e_{zx}}{\partial z}\big) \end{pmatrix} \end{aligned}$$
を定義すると、その成分を計算することにより
$$\begin{aligned} \DIV T^e=\varepsilon_0(\DIV\bm E)\bm E+\varepsilon_0(\rot\bm E)\times\bm E \end{aligned}$$
となることを確かめられる。
同様に、
$$\begin{aligned} T^m=\frac{1}{\mu_0}\Big[\bm B\bm B^T-\frac{1}{2}(\bm B^T\bm B) I\Big]\\ \end{aligned}$$
と置く時、$T=T^e+T^m$ を Maxwell の応力テンソルと呼ぶ。
電磁場の運動量・電磁場の及ぼす応力 †
この $T$ を用いることにより、
$$\begin{aligned} \frac{d}{dt}\Big[\underbrace{\sum_km_k\dot{\bm z}_k(t)}_\text{全粒子の運動量}+ \int d^3x\underbrace{\rule[-3ex]{0pt}{1pt}\Big\{\frac{1}{c^2}\bm S(\bm x,t)\Big\}}_\text{電磁場の運動量密度}\Big]\\ =\int d^3x\,\DIV T(\bm x,t)=\underbrace{\int_S T(\bm x,t)\bm ndS\rule[-3ex]{0pt}{1pt}}_\text{界面にて系に加えられる外力} \end{aligned}$$
のように書き表せる。
- 左辺2項目は電磁場の持つ運動量で、その単位体積あたりの密度は
ポインティングベクトルを使って $\bm S(\bm x,t)/c^2$ と表せる - 右辺は外界から系に加わる力で、界面部分の電磁場の値のみを用いて書かれている
- 外界から系に加わる力は必ずしも界面に垂直とは限らず、 界面に水平な成分も持っている。これは、 $T\bm n$ が必ずしも $\bm n$ と平行にならないことから分かる。
図で表わすと †
すべての質点(点電荷)を含む閉曲面 $S$ と、$S$ に囲まれる体積 $V$ を考える。
全質点の運動量の他に、電磁場の存在する空間自体が運動量を持つというのが上での結論。
微小体積 $d^3x$ の持つ運動量は、体積に運動量密度を掛けて $d\bm p=\frac{1}{c^2}\bm S(\bm x,t)d^3x$ と表せる。
系に及ぼされる外力は界面 $S$ における Maxwell 応力を積分することにより求められる。
微小面積 $dS$ にかかる応力は、法線ベクトルに応力テンソル $T$ を掛けて求められ、 $d\bm f=T\bm ndS$ と表せる。
この描像では個々の質点がうけるローレンツ力は、系の部分と部分との間の相互作用であるため、全運動量の変化に影響しないとして無視できる。
近接相互作用の視点から見れば、個々の質点が感じるローレンツ力は、 まさに質点の存在する点に存在する電磁場との相互作用であり、 系内部での運動量のやりとりにしかならない(全運動量に寄与しない)。 これに対し、系外部との運動量のやりとりは界面 $S$ 上でのみで起きていることになる。
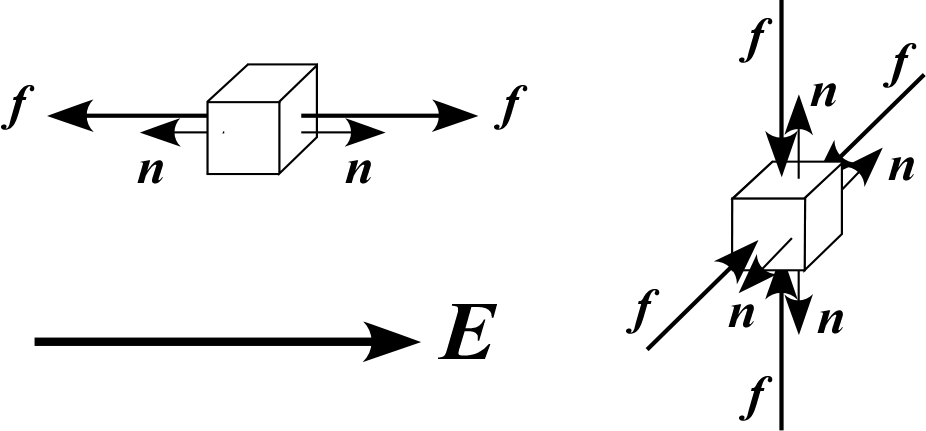
例:一様な電磁場 †
$\bm E=(0\ 0\ E_z)$ のとき、
$$\begin{aligned}T=T^e=\varepsilon_0\begin{pmatrix}-\frac{1}{2}E_z^2&&\\ &-\frac{1}{2}E_z^2&\\ &&\frac{1}{2}E_z^2 \end{pmatrix}\end{aligned}$$
となる。
これは必ずしも全空間で一様な電場を考えているわけではなく、局所的に電場が一様と思えるくらいの小さな領域に電場と同じ方向に $z$ 軸を取ったと思えば良い。
電場に垂直な面への外力:
$\bm n=(0\ 0\ \pm1)\parallel\bm E$ の時、$T\bm n=\frac{\varepsilon_0}{2}E_z^2\bm n$
力は常に $\bm n$ と同じ向きになることが分かる。 すなわち微小領域における電場に垂直な界面には引っ張り(外向き)の応力がかかることになる。
電場に平行な面への外力:
$\bm n=(\pm 1\ 0\ 0)\perp\bm E$ あるいは $\bm n=(0\ \pm 1\ 0)\perp\bm E$ の時、 $T\bm n=-\frac{\varepsilon_0}{2}E_z^2\bm n$
力は常に $\bm n$ に反平行になることが分かる。 すなわち微小領域における電場に平行な界面には圧縮(内向き)の応力がかかることになる。
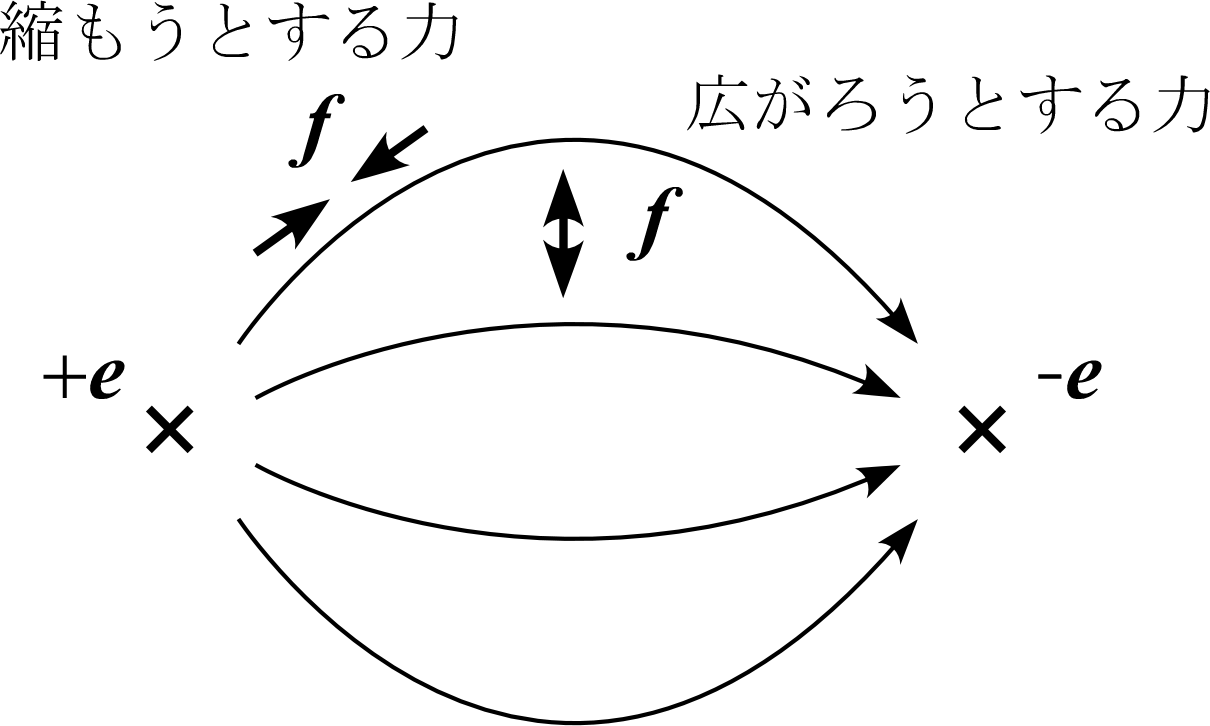
微小領域がそのような外力を受ける理由として、電気力線には長さ方向に縮もうとする方向に、 また、線間をなるべく広く取ろうとする方向に力を生じる性質があるとする古典的な解釈が 役に立つ。
微小領域が引っ張りの外力を受けているとき、微小領域自体は逆に外部領域を引っ張ろうとしている。 逆に、微小領域が押しつぶされるような外力を受けているとき、微小領域は外部領域を押し返している。 微小領域が受ける外力と、微小領域が外部領域に及ぼす力とは、作用と反作用の関係になるのである。
電気力線が線に沿って縮もうとするのは微小領域が外部領域を引っ張ることに相当し、 線間を広げようとするのは微小領域が外部領域を押し返すことに相当する。
このような電気力線による応力の理解は、静電気力の近接相互作用による描像と整合性が高い。 電荷同士が遠隔的に相互作用するのではなく、電荷はすぐ側の電気力線により引っ張られる。 電気力線自体も、電気力線に沿った方向、電気力線に垂直な方向に応力を感じながら空間に張られる。
質問・コメント †
電荷保存則の途中式について †
初学者? ()
初めまして。分かりやすい資料ありがとうございます。
質問なのですが、電荷保存則が成り立つか確認する箇所で
電荷密度の時間tによる偏微分をおこない、その結果、右辺で,ベクトルxによる偏微分が出てきていると思います.
勉強不足の私からすると,ベクトルxは時間を引数に持たないので,ここでは連鎖率により,ベクトルz(t)による偏微分がでてくるのではないかと考えてしまいます.
何故,ベクトルz(t)による偏微分ではなく,ベクトルxによる偏微分なのでしょうか.
お手数おかけしますが、よろしくお願いします.
- こちらを参考にしてください。$$\begin{aligned} \rho(\bm x,t+\Delta t) &=e\delta^3(\bm x-\bm z(t+\Delta t))\\ &=e\delta^3(\bm x-\bm z(t)-\dot{\bm z}\Delta t)\\ &=\underbrace{e\delta^3(\bm x-\bm z(t))}_{\rho(\bm x,t)}+\big[-e\dot{\bm z}\cdot\text{grad}\,\delta^3(\bm x-\bm z(t))\big]\Delta t\\ \end{aligned}$$ -- 武内(管理人)?
- 丁寧な解説,ありがとうございました.おかげ様で理解できました. -- 初学者?
*1 以前は「ラジオメーター」 により光の運動量を目で見ることができると記述していたのですが、これは誤りとのこと。https://ja.wikipedia.org/wiki/ラジオメーター効果#誤った原理説明 すみませんでした。
添付ファイル: