スピントロニクス理論の基礎/8-10 のバックアップ(No.7)
更新- バックアップ一覧
- 差分 を表示
- 現在との差分 を表示
- ソース を表示
- スピントロニクス理論の基礎/8-10 へ行く。
8-10 不純物散乱の元での Green 関数 †
(8.116)
&math( &v_i(\bm q)\equiv \frac{1}{V}\int d^3re^{i\bm q\cdot\bm r}v_i(\bm r)\\ &=\frac{1}{V}\sum_k^{N_i}v_ka^3\int d^3re^{i\bm q\cdot\bm r}[\delta(\bm r-\bm R_k)-1/V]\\ &=\frac{a^3}{V}\sum_k^{N_i}v_k(e^{i\bm q\cdot\bm R_k}-\delta_{\bm q,0}) );
を不純物散乱ポテンシャルの Fourier 変換と定義する。
この定義は (8.74) 等に与えられた の Fourier 変換とは の配置や の符号などが異なるので注意が必要。
これに対応するハミルトニアンは、
(8.116)
&math( &V_i=\int d^3rv_i(\bm r)c^\dagger(\bm r)c(\bm r)\\ &=\int d^3r \left(\sum_{\bm q}e^{-i\bm q\cdot\bm r}v_i(\bm q)\right) \left(\frac{1}{\sqrt V}\sum_{\bm k}e^{-i\bm k\cdot\bm r}c_{\bm k}^\dagger\right) \left(\frac{1}{\sqrt V}\sum_{\bm k'}e^{i\bm k'\cdot\bm r}c_{\bm k'}\right)\\ &=\sum_{\bm q,\bm k,\bm k'}v_i(\bm q)c_{\bm k}^\dagger c_{\bm k'}\frac{1}{V}\int d^3re^{i(-\bm q-\bm k+\bm k')\cdot\bm r}\\ &=\sum_{\bm q,\bm k,\bm k'}v_i(\bm q)c_{\bm k}^\dagger c_{\bm k'}\delta_{\bm q+\bm k,\bm k'}\\ &=\sum_{\bm q,\bm k}v_i(\bm q)c^\dagger(\bm k)c(\bm k+\bm q) );
となる。
今考えているようなポテンシャルでは電子の振動数が変わらないため、単一の によって表すことができる。
&math(g_{\bm k,\bm k',\omega,\omega'}= 2\pi \delta(\omega-\omega')g_{\bm k,\bm k',\omega});
さらに 8-7 で見たように、 に関しては、単一の で表せる。
&math(g_{0\bm k,\bm k',\omega}= \delta_{\bm k,\bm k'}g_{0\bm k,\omega});
(8.117)
係数を正しく付けるために次元について確認
- は (8.76) によれば で無次元、 で無次元、 が残って (時間/エネルギー) の次元を持つ
- は が外に出るので、(1/エネルギー) の次元を持つ
- は (8.116) によれば と同じ次元で、これは (エネルギー) の次元を持つ
実のところ、ここでのフーリエ係数の定義は係数の付け方などが非常に特殊なので、 慎重に計算していかないと正しい答えが得られない。実際に計算を進めるとかなり大変。
&math( &g_{\bm k,\bm k',\omega,\omega'}^r= \frac{1}{\hbar V}\int dt\int dt'\int d^3r\int d^3r' e^{i(\omega t-\omega't'-\bm k\cdot\bm r+\bm k'\cdot\bm r')}g^r(\bm r,t,\bm r',t')\\ &= \frac{1}{\hbar V}\int dt\int dt'\int d^3r\int d^3r' e^{i(\omega t-\omega't'-\bm k\cdot\bm r+\bm k'\cdot\bm r')} g_0^r(\bm r,t,\bm r',t')\\ &+ \frac{1}{\hbar V}\int dt\int dt'\int d^3r\int d^3r' e^{i(\omega t-\omega't'-\bm k\cdot\bm r+\bm k'\cdot\bm r')} \frac{1}{\hbar}\int dt_1\int d^3r_1 g_0^r(\bm r,t,\bm r_1,t_1)v_i(\bm r_1)g^r(\bm r_1,t_1,\bm r',t')\\ &= g_{0\bm k,\bm k',\omega,\omega'}^r+ \frac{1}{\hbar^2 V}\int dt_1\int d^3r_1 \int dt\int dt'\int d^3r\int d^3r' e^{i(\omega t_1-\omega't'-\bm k\cdot\bm r_1+\bm k'\cdot\bm r')} \\ &\hspace{1cm}\times e^{i\omega (t-t_1)}e^{-i\bm k\cdot(\bm r-\bm r_)} g_0^r(\bm r-\bm r_1,t-t_1)v_i(\bm r_1)g^r(\bm r_1,t_1,\bm r',t')\\ &= 2\pi\delta(\omega-\omega')\delta_{\bm k,\bm k'}g_{0\bm k,\omega}^r+ \frac{1}{\hbar V}\int dt_1\int d^3r_1 \int dt'\int d^3r' e^{i(\omega t_1-\omega't'-\bm k\cdot\bm r_1+\bm k'\cdot\bm r')}\\ &\hspace{1cm}\times \left[\frac{1}{\hbar}\int d^3(r-r_1)\int d(t-t_1)e^{-i\bm k\cdot(\bm r-\bm r_)}e^{i\omega (t-t_1)} g_0^r(\bm r-\bm r_1,t-t_1)\right]v_i(\bm r_1)g^r(\bm r_1,t_1,\bm r',t')\\ &=2\pi\delta(\omega-\omega')\delta_{\bm k,\bm k'}g_{0\bm k,\omega}^r+ \frac{g_{0\bm k,\omega}^r}{\hbar V}\int dt_1\int d^3r_1 \int dt'\int d^3r' e^{i(\omega t_1-\omega't'-\bm k\cdot\bm r_1+\bm k'\cdot\bm r')} \Big[\sum_{\bm q}e^{-i\bm q\cdot\bm r_1}v_i(\bm q) \Big] g^r(\bm r_1,t_1,\bm r',t')\\ &=2\pi\delta(\omega-\omega')\delta_{\bm k,\bm k'}g_{0\bm k,\omega}^r+ \frac{g_{0\bm k,\omega}^r}{\hbar V} \sum_{\bm q}v_i(\bm q) \int d^3r_1\int d^3r'\int dt_1\int dt'e^{i(\omega t_1-\omega't'-i(\bm k+\bm q)\cdot\bm r_1+\bm k'\cdot\bm r')} g^r(\bm r_1,t_1,\bm r',t')\\ &=2\pi\delta(\omega-\omega')\delta_{\bm k,\bm k'}g_{0\bm k,\omega}^r+ g_{0\bm k,\omega}^r \sum_{\bm q}v_i(\bm q) g_{\bm k+\bm q,\bm k',\omega,\omega'}^r\\ &=2\pi\delta(\omega-\omega')\left[\delta_{\bm k,\bm k'}g_{0\bm k,\omega}^r+ g_{0\bm k,\omega}^r \sum_{\bm q}v_i(\bm q) g_{\bm k+\bm q,\bm k',\omega}^r\right] );
したがって、
&math(&g_{\bm k,\bm k',\omega}^r=\delta_{\bm k,\bm k'}g_{0\bm k,\omega}^r+ g_{0\bm k,\omega}^r \sum_{\bm q}v_i(\bm q) g_{\bm k+\bm q,\bm k',\omega}^r);
(8.74)〜(8.76) や (8.116) のフーリエ変換の定義で係数がいろいろ工夫してある。 を埋め込む場所が と で異なったり、 数学的には意味のない が埋め込まれていたり。
これらの工夫は上式で余計な係数が出てこないようにするための、 細心の注意を払った定義であったことがここへ来て始めて分かった。
もう一度次元を確認しておくと、
- および は (1/エネルギー) の次元
- は (エネルギー) の次元を持っている
右辺の を (8.117) で繰り返し展開すると、
(8.118)
&math( &g_{\bm k,\bm k',\omega}^r=\delta_{\bm k,\bm k'}g_{0\bm k,\omega}^r+ g_{0\bm k,\omega}^r \sum_{\bm q}v_i(\bm q) \big(\delta_{\bm k+\bm q,\bm k'}g_{0\bm k+\bm q,\omega}^r+ g_{0\bm k+\bm q,\omega}^r \sum_{\bm q'}v_i(\bm q')g_{\bm k+\bm q+\bm q',\bm k',\omega}^r \big)\\ &=g_{0\bm k,\omega}^r\delta_{\bm k,\bm k'}+ \sum_{\bm q}v_i(\bm q) g_{0\bm k,\omega}^r g_{0\bm k+\bm q,\omega}^r \delta_{\bm k+\bm q,\bm k'}+ \sum_{\bm q,\bm q'}v_i(\bm q) g_{0\bm k,\omega}^r g_{0\bm k+\bm q,\omega}^r v_i(\bm q')g_{\bm k+\bm q+\bm q',\bm k',\omega}^r\\ &=g_{0\bm k,\omega}^r\delta_{\bm k,\bm k'}+ \sum_{\bm q_1}v_i(\bm q_1) g_{0\bm k,\omega}^r g_{0\bm k+\bm q_1,\omega}^r \delta_{\bm k+\bm q_1,\bm k'}+ \sum_{\bm q_1,\bm q_2} g_{0\bm k,\omega}^r v_i(\bm q_1)g_{0\bm k+\bm q_1,\omega}^r v_i(\bm q_2)g_{0\bm k+\bm q_1+\bm q_2,\omega}^r \delta_{\bm k+\bm q_1+\bm q_2,\bm k'}+\dots\\ &+\sum_{\bm q_1,\bm q_2,\dots,\bm q_n} g_{0\bm k,\omega}^r v_i(\bm q_1)g_{0\bm k+\bm q_1,\omega}^r v_i(\bm q_2)g_{0\bm k+\bm q_1+\bm q_2,\omega}^r \dots v_i(\bm q_{n-1})g_{0\bm k+\bm q_1+\dots+\bm q_{n-1},\omega}^r v_i(\bm q_n)g_{0\bm k+\bm q_1+\dots+\bm q_n,\omega}\, \delta_{\bm k+\bm q_1+\dots+\bm q_n,\bm k'}\\ &+\dots\\ );
特徴を見ておくと、
- 次の項には 個の が現われ、
- その間に 個の が入っている
- 一番右の は 関数により に等しくなるため、 個の のうち実質的に自由に動かせるのは 個である。
や の中に現われる和について不純物の位置平均 を取る。
(8.119A)
&math(&\langle \sum_{k=1}^{N_i}e^{\textcolor{red}{i}\bm q\cdot\bm R_k}\rangle_i \equiv \frac{1}{V^{N_i}}\int d^3R_{1}\int d^3R_{2}\dots\int d^3R_{N_i} \sum_{k=1}^{N_i}e^{\textcolor{red}{i}\bm q\cdot\bm R_k}\\ &=\sum_{k=1}^{N_i} \frac{1}{V}\int d^3R_k e^{\textcolor{red}{i}\bm q\cdot\bm R_k} = N_i\delta_{\bm q,\bm 0});
&math( &\langle \sum_{k_1,k_2}e^{\textcolor{red}{i}\bm q_1\cdot\bm R_{k_1}}e^{\textcolor{red}{i}\bm q_2\cdot\bm R_{k_2}} \rangle_i\\ &=\frac{1}{V^{N_i}}\int d^3R_{1}\int d^3R_{2}\dots\int d^3R_{N_i} \sum_{k_1,k_2}e^{\textcolor{red}{i}\bm q_1\cdot\bm R_{k_1}}e^{\textcolor{red}{i}\bm q_2\cdot\bm R_{k_2}} \\ &= \sum_{k_1\ne k_2} \frac{1}{V} \int d^3R_{k_1}\int d^3R_{k_2} e^{\textcolor{red}{i}\bm q_1\cdot\bm R_{k_1}}e^{\textcolor{red}{i}\bm q_2\cdot\bm R_{k_2}}
- \sum_{k} \frac{1}{V} \int d^3R_{k} e^{\textcolor{red}{i}\bm q_1\cdot\bm R_{k}}e^{\textcolor{red}{i}\bm q_2\cdot\bm R_{k}}\\ &= N_i(N_i-1)\delta_{\bm q_1,\bm 0}\delta_{\bm q_2,\bm 0} + N_i\delta_{\bm q_1+\bm q_2,\bm 0} );
&math( &\langle \sum_{k_1,k_2,k_3}e^{\textcolor{red}{i}\bm q_1\cdot\bm R_{k_1}}e^{\textcolor{red}{i}\bm q_2\cdot\bm R_{k_2}}e^{\textcolor{red}{i}\bm q_2\cdot\bm R_{k_3}} \rangle_i\\ &= \sum_{k_1\ne k_2 \ne k_3} \delta_{\bm q_1,0}\delta_{\bm q_2,0}\delta_{\bm q_3,0}
- \sum_{k_1 = k_2 \ne k_3} \delta_{\bm q_1+\bm q_2,0}\delta_{\bm q_3,0}
- \sum_{k_1 \ne k_2 = k_3} \delta_{\bm q_1,0}\delta_{\bm q_2+q_3,0}
- \sum_{k_1 = k_3 \ne k_2} \delta_{\bm q_1+\bm q_3,0}\delta_{\bm q_2,0}
- \sum_{k_1 = k_3 = k_2} \delta_{\bm q_1+\bm q_2+\bm q_3,0}\\ &= N_i(N_i-1)(N_i-2)\delta_{\bm q_1,\bm 0}\delta_{\bm q_2,\bm 0}
- N_i(N_i-1)(\delta_{\bm q_1+\bm q_2,0}\delta_{\bm q_3,0}+\delta_{\bm q_1,0}\delta_{\bm q_2+q_3,0}+\delta_{\bm q_1+\bm q_3,0}\delta_{\bm q_2,0})
- N_i\delta_{\bm q_1+\bm q_2+\bm q_3,\bm 0} );
ここで、 の成分はゼロなので、 を含む項はすべて消えて、
などとなる。
次の項では、 個の のうち、そのすべてが、 どれか他の と等しくなる項以外は消えることになる。
例えば であれば、
- →
- →
- →
- →
の4つの場合以外の項は消えて、これらが (8.135)〜(8.139) で評価されている4つの場合に相当する。
このようにして現われる 関数の部分に注目すると、 たとえば は の時以外ぜろとなるため、 この項を評価するに当たっては、 と仮定して良い。
同様に、 次に現われるすべての項で を仮定できる。
すると (8.118) に見るように、すべての 次の項に が含まれているため、
これは、不純物平均により電子の運動量の保存が回復したことに対応している。 (平均により系の並進対称性が回復したと言い換えても良い、らしい)
そこで、
(8.121)
&math(g_{\bm k,\omega}^r=g_{0\bm k,\omega}^r+ n_iv_i^2\frac{1}{N}\sum_{\bm q_1}g_{0\bm k,\omega}^r g_{0\bm k+\bm q_1,\omega}^r g_{0\bm k,\omega}^r+ n_iv_i^3\frac{1}{N^2}\sum_{\bm q_1,\bm q_2}g_{0\bm k,\omega}^r g_{0\bm k+\bm q_1,\omega}^r g_{0\bm k+\bm q_1+\bm q_2,\omega}^r g_{0\bm k,\omega}^r+ \cdots);
などとなる。
2次の項に現われる に対する和は、 を新しい変数と考えると独立に評価することができて、
(8.122)
&math( \frac{1}{N}\sum_{\bm q_1}g_{\textcolor{red}{0}\bm k+\bm q_1,\omega}^r= \frac{1}{N}\sum_{\bm k_1}g_{\textcolor{red}{0}\bm k_1,\omega}^r= a^3\int\frac{d^3k}{(2\pi)^3}g_{\textcolor{red}{0}\bm k_1,\omega}^r= a^3\int\frac{d^3k}{(2\pi)^3}\frac{1}{\hbar\omega-\varepsilon_{\bm k}+i0} );
に対する積分を、 に対する積分に置き換えると、 ( は 分散関係)
(8.123)
&math( \frac{1}{N}\sum_{\bm q_1}g_{\textcolor{red}{0}\bm k+\bm q_1,\omega}^r= \int_{-\epsilon_F}^\infty d\varepsilon\nu(\varepsilon)\frac{1}{\hbar\omega-\varepsilon+i0} );
これ、本当は δ関数の性質 を使うとまともに計算できるんだけど、 まずはしばらく教科書の通りやってみる。
(8.124)
から始めればいいのかな?
&math( \nu(\varepsilon)\equiv\frac{V}{N(2\pi)^3}\frac{d^3k}{d\varepsilon}=\frac{a^3}{2\pi^3}\frac{k^2dk}{d\varepsilon} =\frac{mk}{2\pi^2\hbar^2}a^3 =\frac{m^{3/2}a^3}{\sqrt 2\pi^2\hbar^3}\sqrt{\varepsilon+\varepsilon_F} );
などを使った。
(8.125)
は 付近でのみ大きな値を取る。そこで、
&math( \int_{-\epsilon_F}^\infty d\varepsilon\nu(\varepsilon)\frac{1}{\hbar\omega-\varepsilon+i0}\sim \nu(\hbar\omega)\int_{-\infty}^\infty d\varepsilon\frac{1}{\hbar\omega-\varepsilon+i0} );
どうして教科書で でなく になっているのか分からない・・・
グリーン関数に という項が出てくることと、 最終的にフェルミレベル付近、すなわち しか考えないことから、 として大丈夫、とかいうことなんだろうか?
&math(\frac{1}{N}\sum_{\bm k}g_{\bm k,\omega}^r\sim \nu(0)\int_{-\infty}^\infty d\varepsilon\frac{1}{-\varepsilon+i0} =\nu(0)\int_{-\infty}^\infty d\varepsilon\frac{-\varepsilon-i0}{\varepsilon+(0)^2} \ \textcolor{red}{\stackrel{?}{=}}\,-\pi i\nu(0) );
うーん、これって説明になっているんだろうか?なんだかよく分からない。
(9.18) あたりでもう少しまじめにやると書いてあるので重複するかもしれないけれど、 δ関数の性質 を使って少しちゃんとやってみる。
&math( &\int_{-\epsilon_F}^\infty d\varepsilon\nu(\varepsilon)\frac{1}{\hbar\omega-\varepsilon+i0}\\ &=-\int_{\epsilon_F+\hbar\omega}^{-\infty} d\varepsilon'\nu(\hbar\omega-\varepsilon')\frac{1}{\varepsilon'+i0}\\ &=\int_{-\infty}^{\epsilon_F+\hbar\omega} d\varepsilon'\nu(\hbar\omega-\varepsilon')\frac{1}{\varepsilon'+i0}\\ &=\int_{-\infty}^{\epsilon_F+\hbar\omega} d\varepsilon'\nu(\hbar\omega-\varepsilon')
\left[\frac{1}{\varepsilon'}-i\pi\delta(\varepsilon')\right]\\
&=\left[\ \frac{m^{3/2}a^3}{\sqrt 2\pi^2\hbar^3}\int_{-\infty}^{\epsilon_F+\hbar\omega} d\varepsilon'\frac{\sqrt{\hbar\omega-\varepsilon'+\varepsilon_F}}{\varepsilon'}\ \right]
- i\pi\nu(\hbar\omega)\\ );
この第一項、実数成分の被積分関数は の時に と見なすことができるから、 この積分は発散する。しかし、今は件の積分の虚数成分のみに興味があって、 実数成分は無視してしまって良いらしい。これは (8.126) の直後の 注11) の通り。
虚数成分にはやはり ではなく が出てくることが確かめられたが、以降では教科書通り で進めてみる。
(8.127)
&math( &g_{\bm k,\omega}^r=g_{0\bm k,\omega}^r- n_iv_i^2 \pi i\nu(0)(g_{0\bm k,\omega}^r)^2+\cdots\\ &=g_{0\bm k,\omega}^r- \frac{i\hbar}{2\tau}(g_{0\bm k,\omega}^r)^2+\cdots\\ );
ここで、
(8.128)
この は電子エネルギーのぼやけであることが後に分かる。
そこで、系が金属であるための条件
(8.129)
を先取りして用いていく。
(8.130)
を計算するに当たり、
- 0次には1つも無いが
- 1次は を1つ
- 2次は を2つ
- ・・・
含んでいる。
不純物平均により、複数の に共通の がかかり、 が現われる項以外が消えてしまうため、
(8.131), (8.132)
のように、 個の を必ず2本以上束ねた項だけが残る。
(8.134)
(8.121) の3次の項に出てくる和は、 、 と置けば、
&math( &\sum_{\bm q_1,\bm q_2}g_{0\bm k,\omega}^rv_i(\bm q_1)g_{0\bm k+\bm q_1,\omega}^rv_i(\bm q_2)g_{0\bm k+\bm q_1+\bm q_2,\omega}^r v_i(\bm q_3=-\bm q_1-\bm q_2)g_{0\bm k,\omega}^r\\ &=n_iv_i^3\textcolor{red}{\frac{1}{N^2}}\sum_{\bm q_1,\bm q_2}g_{0\bm k,\omega}^r g_{0\bm k+\bm q_1,\omega}^r g_{0\bm k+\bm q_1+\bm q_2,\omega}^r g_{0\bm k,\omega}^r\\ &=n_iv_i^3g_{0\bm k,\omega}^r \Big(\textcolor{red}{\frac{1}{N}}\sum_{\bm k_1}g_{0\bm k_1,\omega}^r\Big)\Big(\textcolor{red}{\frac{1}{N}}\sum_{\bm k_2}g_{0\bm k_2,\omega}^r\Big) g_{0\bm k,\omega}^r\\ &=n_iv_i^3g_{0\bm k,\omega}^r \Big(\textcolor{red}{\frac{1}{N}}\sum_{\bm k_1}g_{0\bm k_1,\omega}^r\Big)^2 g_{0\bm k,\omega}^r\\ &=n_iv_i^3g_{0\bm k,\omega}^r \big(-\pi i\nu(0)\big)^2 g_{0\bm k,\omega}^r\\ &=-\frac{\textcolor{red}{\hbar}}{2\tau}v_i\pi \nu(0)\big(g_{0\bm k,\omega}^r \big)^2\\ );
(8.135)
すなわち の項で、 とすれば、
&math( &\sum_{\bm q_1,\bm q_2}g_{0\bm k,\omega}^rv_i(\bm q_1)g_{0\bm k+\bm q_1,\omega}^rv_i(-\bm q_1)g_{0\bm k,\omega}^rv_i(\bm q_3)g_{0\bm k+\bm q_3,\omega}^rv_i(-\bm q_3)g_{0\bm k,\omega}^r\\ &=n_i^2v_i^4\frac{1}{N^2}\sum_{\bm q_1,\bm q_3}g_{0\bm k,\omega}^r g_{0\bm k+\bm q_1,\omega}^r g_{0\bm k,\omega}^r g_{0\bm k+\bm q_3,\omega}^r g_{0\bm k,\omega}^r\\ &=n_i^2v_i^4\Big(\frac{1}{N}\sum_{\bm k_1}g_{0\bm k+\bm k_1,\omega}^r\Big)^2 \big(g_{0\bm k,\omega}^r\big)^3\\ &=\big(-n_iv_i^2\pi i\nu(0)\big)^2 \big(g_{0\bm k,\omega}^r\big)^3\\ &=\Big(\frac{-i\textcolor{red}{\hbar}}{2\tau}\Big)\big(g_{0\bm k,\omega}^r\big)^3\\);
(8.136)
すなわち の項で、
&math( &\sum_{\bm q_1,\bm q_2,\bm q_3}g_{0\bm k,\omega}^rv_i(\bm q_1)g_{0\bm k+\bm q_1,\omega}^rv_i(\bm q_2)g_{0\bm k+\bm q_1+\bm q_2,\omega}^rv_i(\bm q_3)g_{0\bm k+\bm q_1+\bm q_2+\bm q_3,\omega}^rv_i(-\bm q_1-\bm q_2-\bm q_3)g_{0\bm k,\omega}^r\\ &=n_iv_i^4\frac{1}{N^3}\sum_{\bm q_1,\bm q_2,\bm q_3}g_{0\bm k,\omega}^r g_{0\bm k+\bm q_1,\omega}^r g_{0\bm k+\bm q_1+\bm q_2,\omega}^r g_{0\bm k+\bm q_1+\bm q_2+\bm q_3,\omega}^r g_{0\bm k,\omega}^r\\ &=n_iv_i^4\Big(\frac{1}{N}\sum_{\bm k_1}g_{0\bm k_1,\omega}^r\Big)^3 \big(g_{0\bm k,\omega}^r\big)^2\\ &=n_iv_i^4\big(-\pi i\nu(0)\big)^3 \big(g_{0\bm k,\omega}^r\big)^2\\ &=\frac{i\textcolor{red}{\hbar}}{2\tau}\big(v_i\textcolor{red}{\pi} \nu(0)\big)^2 (g_{0\bm k,\omega}^r\big)^2 );
(8.137)
すなわち の項で、
&math( &\sum_{\bm q_1,\bm q_2}g_{0\bm k,\omega}^rv_i(\bm q_1)g_{0\bm k+\bm q_1,\omega}^rv_i(\bm q_2)g_{0\bm k+\bm q_1+\bm q_2,\omega}^rv_i(-\bm q_2)g_{0\bm k+\bm q_1,\omega}^rv_i(-\bm q_1)g_{0\bm k,\omega}^r\\ &=n_i^2v_i^4\frac{1}{N^2}\sum_{\bm q_1,\bm q_2}g_{0\bm k,\omega}^r g_{0\bm k+\bm q_1,\omega}^r g_{0\bm k+\bm q_1+\bm q_2,\omega}^r g_{0\bm k+\bm q_1,\omega}^r g_{0\bm k,\omega}^r\\ &=n_i^2v_i^4\Big(\frac{1}{N}\sum_{\bm k_1}(g_{0\bm k_1,\omega}^r)^2\Big)\Big(\frac{1}{N}\sum_{\bm k_2}g_{0\bm k_2,\omega}^r\Big) \big(g_{0\bm k,\omega}^r\big)^2\\ &=n_i^2v_i^4\big(\ ?\ \big)\big(-\pi i\nu(0)\big) \big(g_{0\bm k,\omega}^r\big)^2\\ &=n_iv_i^2\big(\ ?\ \big)\big(-\pi i\nu(0)\big) \big(g_{0\bm k,\omega}^r\big)^2\\ &=-\frac{i\hbar}{2\tau}n_iv_i^2\big(\ ?\ \big)\big(g_{0\bm k,\omega}^r\big)^2\\ &=(*) );
の部分は、
&math( &\frac{1}{N}\sum_{\bm k_1}(g_{0\bm k_1,\omega}^r)^2\\ &\sim\nu(0)\int_{-\infty}^\infty d\varepsilon \Big(\frac{1}{-\varepsilon+i0}\Big)^2 &=\nu(0)\int_{-\infty}^\infty d\varepsilon \frac{1}{\varepsilon}\frac{1}{\varepsilon-2i0} &=\nu(0)\int_{-\infty}^\infty d\varepsilon \frac{1}{\varepsilon}\frac{\varepsilon+i0}{\varepsilon^2+(0)^2} );
で、これが
&math( &\frac{1}{N}\sum_{\bm k_1}(g_{0\bm k_1,\omega}^r)^2=-\frac{\pi}{2}i\nu(0)\frac{1}{\varepsilon_F} );
であれば、教科書の通り、
&math( (*)=-\frac{1}{2}\Big(\frac{\hbar}{2\tau}\Big)^2\frac{1}{\varepsilon_F}\big(g_{0\bm k,\omega}^r\big)^2 );
となるけれど、 が出てくる理由など今のところ不明。
δ関数の性質 で予想した値を使うと、 この積分からは (8.123)〜(8.126) と同様に実数部分と虚数部分の両方が出てくるはずで、 ここでの結果のように虚数成分のみにはならない。(8.123)〜(8.126) と異なりここでの計算で 実数成分を無視してはいけないように思うし、そもそも虚数成分でさえも発散しそうに思える。
この点はセミナーの時に教えてもらわないと自分では解決できない感じ。
(8.138)
&math(&\sum_{\bm q_1,\bm q_2}g_{0\bm k,\omega}^rv_i(\bm q_1)g_{0\bm k+\bm q_1,\omega}^rv_i(\bm q_2)g_{0\bm k+\bm q_1+\bm q_2,\omega}^rv_i(-\bm q_1)g_{0\bm k+\bm q_2,\omega}^rv_i(-\bm q_2)g_{0\bm k,\omega}^r\\ &=n_i^2v_i^4\frac{1}{N^2}\sum_{\bm q_1,\bm q_2}g_{0\bm k,\omega}^r g_{0\bm k+\bm q_1,\omega}^r g_{0\bm k+\bm q_1+\bm q_2,\omega}^r g_{0\bm k+\bm q_2,\omega}^r g_{0\bm k,\omega}^r\\ &=n_i^2v_i^4\textcolor{red}{\frac{1}{N^2}}\big(g_{0\bm k,\omega}^r\big)^2 \sum_{\bm k_1,\bm k_2} g_{0\bm k_1,\omega}^r \textcolor{red}{g_{0\bm k_1+\bm k_2-\bm k,\omega}^r g_{0\bm k_2,\omega}^r} \\);
と置いた。
最後の式の と とを入れ替えると教科書の式になるのだけれど、入れ替えて良いのかどうか疑問。 この違いは以下で見るように、近似の元で最終結果には効いてこない。
この次に出てくる説明はいろいろおかしいと思う。たぶん正しいのは以下。
- は 付近でのみ大きな値を取る ← ということか?
- が大きな値を取るのは となるときのみ
-
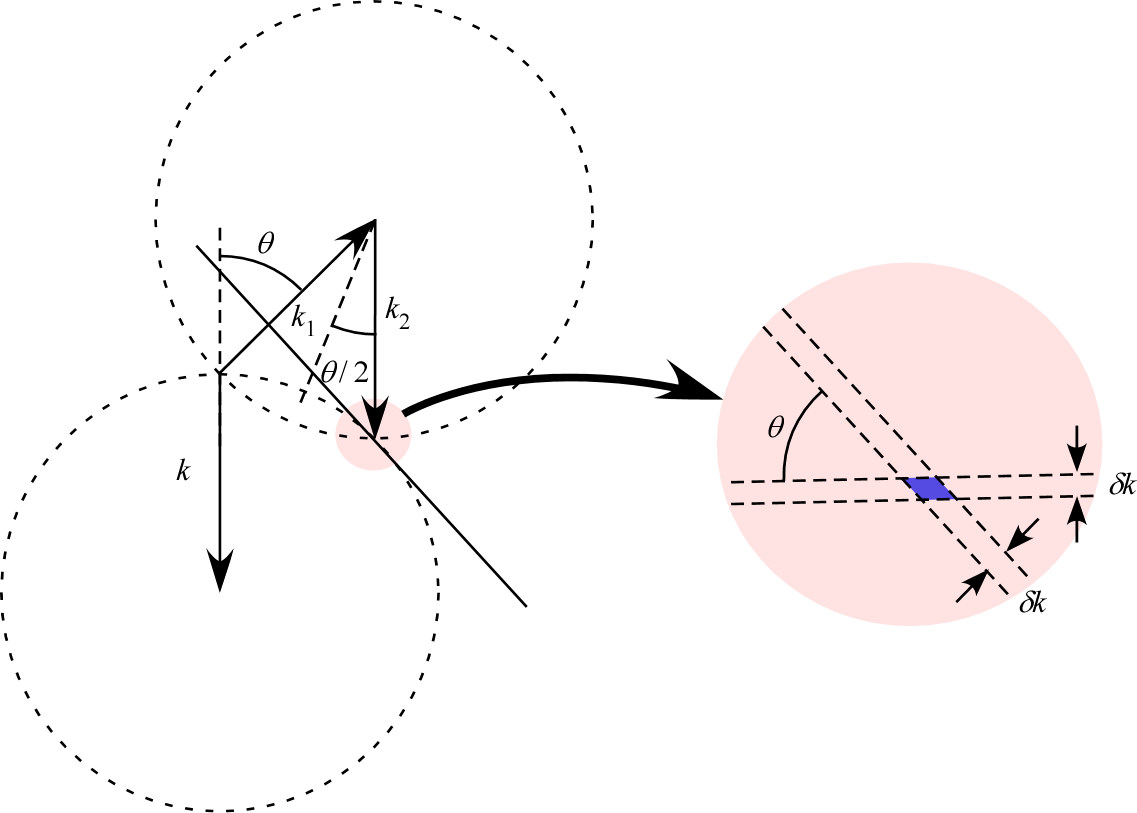
について考えると、
- 与えられた に対して任意の を選ぶことができるが、
- は となる球面上に来るように選ばなければならない
- これは原点を中心とした半径 の球殻と、 を中心とした半径 の球殻との交線上に が来ることと同義である
- フェルミ面のぼやけを 程度と仮定すると、
- を完全に自由に取れば が球殻の体積であるが、
-
のために上記の円弧状の交線に限られると、体積はどれほど減るだろうか?
- と とが為す角を とすると、
- 円弧の半径は で、円周は
- 円弧の太さ(断面積)は
- したがって、円弧の体積は
- この値は で発散するが、このとき の側の選択肢がほぼゼロになるので問題ない
-
が動いたことを想定し、
に対して平均を取ると、
&math(&\frac{1}{4\pi}\int_0^\pi d\theta\int_0^{2\pi}\sin\theta d\psi \frac{2\pi k_F\delta k^2\sin(\theta/2)}{\sin\theta}\\ &=\frac{2\pi k_F\delta k^2}{2}\int_0^\pi d\theta\sin(\theta/2)\\ &=\frac{2\pi k_F\delta k^2}{2}[-2\cos(\theta/2)]_0^\pi\\ &=2\pi k_F\delta k^2);
- したがって、完全に自由に を取ったときに比べて値は だけ小さくなる
- フェルミレベル近傍に於いて より、 となる。
ということで、ちょっと意味は無いけれど本文中の誤植のみ指摘:
閑話休題して、
(8.139)
「自由に取った場合」を考えるには、 を数えるときに が2つ掛かっていることを考慮して (8.137) に帰着することが分かる。
&math( &n_i^2v_i^4\textcolor{red}{\frac{1}{N^2}}\big(g_{0\bm k,\omega}^r\big)^2 \sum_{\bm k_1,\bm k_2} g_{0\bm k_1,\omega}^r g_{0\bm k_2,\omega}^r g_{0\bm k+\bm k_2-\bm k_1,\omega}^r \\ &\sim \left(\frac{\hbar}{4\varepsilon_F\tau}\right)n_i^2v_i^4\textcolor{red}{\frac{1}{N^2}}\big(g_{0\bm k,\omega}^r\big)^2 \sum_{\bm k_1,\bm k_2} g_{0\bm k_1,\omega}^r \big(g_{0\bm k_2,\omega}^r\big)^2 \\ &=-\left(\frac{\hbar}{4\varepsilon_F\tau}\right) \frac{1}{2}\Big(\frac{\hbar}{2\tau}\Big)^2\frac{1}{\varepsilon_F}\big(g_{0\bm k,\omega}^r\big)^2\\ &\propto \frac{\hbar}{\tau}\left(\frac{\hbar}{\varepsilon_F\tau}\right)^2\big(g_{0\bm k,\omega}^r\big)^2 );
各項の大きさを評価するため、 の大きさを評価しておく。
がフェルミエネルギーであることから(実際にはこの分を引いてあるため 0 がフェルミエネルギーである)
&math( &\int_{-\epsilon_F}^0\nu(\varepsilon)d\varepsilon=1\\ &=\int_{-\epsilon_F}^0 d\varepsilon \frac{m^{3/2}a^3}{\sqrt 2\pi^2\hbar^3}\sqrt{\varepsilon+\varepsilon_F}\\ &=\frac{m^{3/2}a^3}{\sqrt 2\pi^2\hbar^3}\int_0^{\epsilon_F} d\varepsilon' \sqrt{\varepsilon'}\\ &=\frac{m^{3/2}a^3}{\sqrt 2\pi^2\hbar^3}\left[\frac{2}{3}\varepsilon'^{3/2}\right]_0^{\epsilon_F}\\ &=\frac{2\varepsilon_F}{3}\cdot\frac{m^{3/2}a^3}{\sqrt 2\pi^2\hbar^3}\sqrt{\varepsilon_F}\\ &=\frac{2\varepsilon_F}{3}\nu(0) );
したがって、
金属であるためには、
が必要である。
&math( &3\pi n_iv_i^2\ll\varepsilon_F^2\\ &(3\pi n_i)^\frac{1}{2}v_i\ll\varepsilon_F\\ );
と書き直せば、これは不純物のポテンシャルがフェルミエネルギーに比べて小さく、 さらに不純物密度が高すぎないことを示している。
これに加えて、
すなわち
を仮定すると、
(8.140)
&math( g_{\bm k,\omega}^r= g_{0\bm k,\omega}^r+\left(-\frac{i\hbar}{2\tau}\right)(g_{0\bm k,\omega}^r)^2 \left[ 1\textcolor{red}{-}i\pi v_i\nu(0)-(\textcolor{red}{\pi}v_i\nu(0))^2
- \frac{i}{4}\frac{\hbar}{\varepsilon_F\tau}+O\left(\frac{\hbar}{\varepsilon_F\tau}\right)^2+\cdots \right]+ \left(-\frac{i\hbar}{2\tau}\right)^2(g_{0\bm k,\omega}^r)^3+\cdots );
の [ ] の中は1を残して消し去ることができる。
同様にして、高次項を評価すれば2次の項やそれ以降にも小さな項が付け加わるが、 上記の2つの条件下ではやはり無視できて、
(8.141)
&math( \frac{g_{\bm k,\omega}^r}{g_{0\bm k,\omega}^r}= 1+\left(-\frac{i\hbar}{2\tau}g_{0\bm k,\omega}^r\right)+ \left(-\frac{i\hbar}{2\tau}g_{0\bm k,\omega}^r\right)^2+\cdots =\frac{1}{1+\frac{i\hbar}{2\tau}g_{0\bm k,\omega}^r} );
&math( g_{\bm k,\omega}^r= \frac{1}{(g_{0\bm k,\omega}^r)^{-1}+\frac{i\hbar}{2\tau}} =\frac{1}{\hbar\omega-\varepsilon_{\bm k}+\frac{i\hbar}{2\tau}} );
となる。
本文中で などと書いてあるが、 これは の間違いか?
結局、元々の偶数次項から出てくる「2次の寄与と同様な物が繰り返される項」、 すなわち となる項が支配的な寄与を及ぼし、他の項は無視できることになる。
(8.142)
&math( g_{\bm k,\omega}^a =\frac{1}{\hbar\omega-\varepsilon_{\bm k}-\frac{i\hbar}{2\tau}} );
不純物散乱がない場合には のために非常に急峻に変化する 関数であったが、不純物散乱によってピーク幅が広がっている、 すなわちフェルミレベルがぼやけている、ということになる。
「自己エネルギー」についてはここだけ読んでもよく分からないので後で勉強が必要。
(8.143)
と置いて、これらを自己エネルギーと呼べば、
(8.144)
&math( g_{\bm k,\omega}^r =\frac{1}{\hbar\omega-\varepsilon_{\bm k}-\Sigma^r} );
&math( g_{\bm k,\omega}^a =\frac{1}{\hbar\omega-\varepsilon_{\bm k}-\Sigma^a} );
の部分が虚数であることが分かりにくい表示になっているので 注意が必要かもしれない。