スピントロニクス理論の基礎/4 のバックアップ(No.5)
更新- バックアップ一覧
- 差分 を表示
- 現在との差分 を表示
- ソース を表示
- スピントロニクス理論の基礎/4 へ行く。
4 強磁性体の微視的記述 †
4-1 強磁性ラグランジアンと磁化の運動 †
(2.12) を極座標表示に直す。
は空間的に大きさは一定で( )、 その方向のみが変化するとすれば、 の方向を表す や を空間座標の関数として、(4.2)
&math( \bm S(\bm r) \equiv S\bm n = \begin{pmatrix} S \sin\theta(\bm r) \cos\phi(\bm r)\\ S\sin\theta(\bm r) \sin\phi(\bm r) \\ S\cos\theta(\bm r) \end{pmatrix} );
と表せる。このとき、
&math( \Delta \theta=\theta(\bm r+\bm a)-\theta(\bm r)=\bm a\cdot \nabla\theta(\bm r) );
&math( \Delta \phi=\phi(\bm r+\bm a)-\phi(\bm r)=\bm a\cdot \nabla\phi(\bm r) );
そして、
のとき
のとき
より、
&math( \sum_{\bm a=a \bm e_x, a\bm e_y, a\bm e_z} &\{\bm S(\bm r+\bm a)-\bm S(\bm r)\}^2\\ &=a^2S^2\{(\nabla\theta)^2+\sin^2\theta(\nabla\phi)^2\}^2 );
したがって、(4.1)
&math( H_J=&\,\frac{J}{2}\sum_{\bm r}\{\nabla \bm S(\bm r)\}^2\\ =&\,\frac{J}{2}\int\frac{d^3r}{a^3}\{\nabla \bm S(\bm r)\}^2\\ =&\,\red{+}\frac{J}{2}\int\frac{d^3r}{a^3}S^2\{(\nabla\theta)^2+\sin^2\theta(\nabla\phi)^2\}^2 );
を得る。(空間的に一様の時に最もエネルギーが低いはずで、教科書の符号は誤り)
磁気異方性 †
(2.12) は物質が等方的な場合の話で、容易軸・困難軸等がある場合には
z軸に向きやすい
や、
y軸に向きにくい
などの項を含める場合もある。
例えば前者の場合が (4.3)
ラグランジアンの導出 †
ハミルトニアンからラグランジアンを求めるには、 スピンを記述する力学変数と、その共役運動量を知る必要がある。
しかしスピンの力学変数 は、半径 の球面上の束縛されているため、 簡単にラグランジアンを求めることができない。
別の言い方をすれば、スピンの量子自由度は SU(2) の交換関係
を満たしており、通常の 通常の 型の交換関係ではないことが 困難の原因となる。
このような場合、簡単にラグランジアンを導出するには経路積分表示をすることになる(らしい)。
そこから求まるのが、(4.5) らしい。
&math( L_S=\int\frac{d^3r}{a^3}\hbar S\dot \phi(\cos\theta-1)-H_S\equiv L_B-H_S );
以下に見るように、スピンのダイナミクスは よりもむしろここで出てくる で規定されるので、本来であれば (4.5) の導出がとても重要なんだけれど・・・ここでは飛ばされている。
運動方程式 †
実際に運動方程式を見てみよう。(4.7)
&math( \frac{d}{dt}\left(\frac{\delta L_S}{\delta \dot \theta}\right)-\frac{\delta L_S}{\delta \theta}=0 );
&math( \frac{d}{dt}\left(\frac{\delta L_S}{\delta \dot \phi}\right)-\frac{\delta L_S}{\delta \phi}=0 );
より、(4.8)
&math( &0-\left(-\hbar S\sin\theta\dot\phi-\frac{\delta H_S}{\delta \theta}\right )=0\\ &\hbar S\sin\theta\dot\phi=-\frac{\delta H_S}{\delta \theta} );
&math( &\frac{d}{dt}(\hbar S(\cos\theta-1))-\frac{\delta H_S}{\delta\phi}=0\\ &\hbar S\sin\theta\dot\theta=-\frac{\delta H_S}{\delta \phi} );
なる、 に対して対称性の良い式を得る。
は汎関数微分を表す。すなわち、 は や の関数であり、 や 自体が の関数である。
言うなれば、 は 座標上のすべての点での 値や 値に依存する多変数関数であり、さらに、 は にも陽に依存している。このような無限個の変数に依存する関数に対する「偏微分」のようなものを書くために汎関数微分が用いられる(そうです)。参照 → http://homepage2.nifty.com/eman/analytic/functional.html
Landau-Lifshitz方程式 †
もう少し見通しを良くするために、ベクトル を用いて書き直す。
&math( \bm S=S\bm n=S\begin{pmatrix}\sin\theta\cos\phi\\ \sin\theta\sin\phi\\ \cos\theta\end{pmatrix} );
より、(4.9), (4,10)
&math( \frac{d\bm S}{dt} &=S\dot\theta\begin{pmatrix}\cos\theta\cos\phi\\ \cos\theta\sin\phi\\ -\sin\theta\end{pmatrix}
- S\dot\phi\begin{pmatrix}-sin\theta\sin\phi\\ \sin\theta\cos\phi\\ 0\end{pmatrix}\\ &\equiv S(\dot\theta\bm e_\theta+\sin\theta\dot\phi\bm e_\phi) );
同様に、
に対して
に対して
ここから、任意の関数 に対して(4.11)
&math( \frac{\delta F}{\delta\theta}=S\left(\bm e_\theta\cdot\frac{\delta F}{\delta\bm S}\right) );
&math( \frac{\delta F}{\delta\phi}=S\sin\theta\left(\bm e_\phi\cdot\frac{\delta F}{\delta\bm S}\right) );
ただし、 は の変化に対する の勾配 の汎関数微分表示である。すなわち、 の変化に対する の変化量が と書けるものとしている。
(4.9) に (4.8) を代入すると、
&math( \hbar \dot{\bm S} &=\left(\frac{1}{\sin\theta}\frac{\delta H_S}{\delta \phi}{\bm e}_\theta-\frac{\delta H_S}{\delta\theta}{\bm e}_\phi\right)\\ &=S\left\{\bm e_\theta\left(\bm e_\phi\cdot\frac{\delta H_S}{\delta\bm S}\right)
- \bm e_\phi\left(\bm e_\theta\cdot\frac{\delta H_S}{\delta\bm S}\right)\right\}\\ );
ベクトル3重積の公式から、一般に
が成り立つので、(4.12)
&math( \hbar \dot{\bm S} &=S\left(\frac{\delta H_S}{\delta\bm S}\times(\bm e_\theta\times\bm e_\phi)\right)\\ &=\frac{\delta H_S}{\delta\bm S}\times \bm S );
ここで、 を用いた。
(4.12) は、ある点 に存在するスピン の運動が、 他のスピン(ここでは隣接するスピン?)の作る に比例する有効磁場の下での歳差運動として記述されることを表している。
ある時刻において、 に存在する有効磁場は(4.13)
と定義される。 は磁気回転比と呼ばれる定数。
これを用いると、(4.14)
となって、一様磁化を持つマクロな強磁性体に対する Landau-Lifshitz 方程式に一致する。
スピンの共役関係 †
(4.5) より、 に共役な変数(運動量) を求めてみる。
ではないのか???
4-2 スピンの Berry 位相項 †
上記の通り、スピン系のラグランジアンの中で が本質的な役割を担う。
これをスピン Berry 位相項と呼ぶ。( の B は Berry の B と思われる)
スピンがゆっくり時間発展するとき、この項によりスピンの波動関数に「位相」が付く・・・ という意味はまだよく分かっていない。
ラグランジアン ( ) の時間積分、作用項を (4.6) の定義に従って計算してみると、
(4.20A)
&math( &\int_{t_0}^{t_1}dt\,L_B\\ &=\int_{t_0}^{t_1}dt\int\frac{d^3r}{a^3}\,\hbar S \dot\phi(\cos\theta-1)\\ &=\int\frac{d^3r}{a^3}\,\hbar S \int_{t_0}^{t_1}dt\, \frac{\PD \phi(\bm r,t)}{\PD t}(\cos\theta(\bm r,t)-1)\\ &=\int\frac{d^3r}{a^3}\,\hbar S \int_{\phi(t_0)}^{\phi(t_1)}\!\! d\phi\, \{\cos\theta(\bm r,t(\phi))-1\}\\ );
となる。さらに
&math( \cos\theta(\bm r,t(\phi))-1=-\int_0^{\theta(\bm r,t(\phi))}d\theta'\,\sin\theta' );
の関係を用いると、
(4.20B)
&math( &\int_{t_0}^{t_1}dt\,L_B\\ &=-\int\frac{d^3r}{a^3}\,\hbar S \int_{\phi(t_0)}^{\phi(t_1)}\!\! d\phi\, \int_0^{\theta(\bm r,t(\phi))}d\theta'\,\sin\theta'\\ );
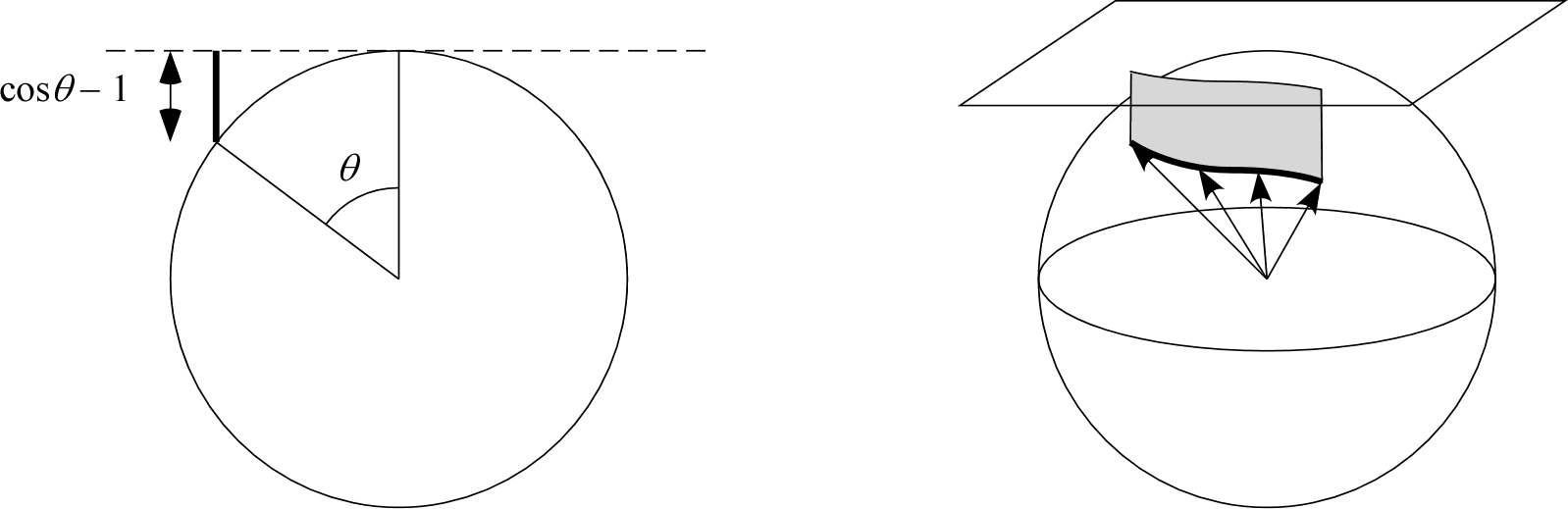
となるが、この式を図4.3左のように図形的に理解したければ、 (4.20A) の方が分かりやすいはずだ。
は上図左のように の方向ベクトル先端から単位球に北極で接する平面に下ろした垂線の足の長さを表している。教科書ではこれが子午線の長さを表しているかの様に書かれているが、その理由はよく分からない。
時刻 と共に が変化すると、この積分値は上図右のように 先端から下ろした垂線が通過する面の面積を表すことに・・・・・あれ、ならないのか。 が面に平行じゃないから簡単には図形で表せないかも?教科書ではこれを北極( )から測った立体角としているが、やはりこれは間違いと感じられる。
また、その後の議論では、 の線に沿って、あるいは の線に沿って、スピンが から まで変化する状況に関して考察されているが、 であるから が時間的に変化しない限り であるため、この議論も意味が分からなかった。
後で文献 [57,58] を当たってみなければ。。。
4-3 スピン系の持つ運動量 †
スピンは角運動量を持つが、通常の運動量を持つか? → YES
まずは一般論から †
一般的に、エネルギーおよび運動量の保存則は系の時間に対する、あるいは空間に対する並進対称性から導かれる。以下にそれを見よう。
系のラグランジアン密度が で表されるとする。このとき系のラグランジアンは、
&math( L(t)\equiv\int d^3r\,\mathcal L(\bm r,t) );
また、系の座標パラメータ を で表す。
は変数 およびその導関数 ただし の関数であるとする。
この場合の古典的な運動方程式は、ラグランジアンの時間積分、すなわちラグランジアン密度の時空積分として定義される作用(action) を極小にするという条件から決まる。
&math( I=\int_{t_1}^{t_2}dt\,L(t)=\int_{t_1}^{t_2}dx_0\int dx_1\int dx_2\int dx_3\,\mathcal L );
すなわち、変数 のいかなる微小変化 に対しても、作用の変化が停留していることになる。
&math( \delta I=\iiiint d^4x\, \frac{\delta I}{\delta \varPsi^\alpha}\delta \varPsi^\alpha=0 );
これが任意の に対して成り立つことから、
が条件となる。上記の通り が と の関数である場合には、
(4.21)
&math( \frac{\delta I}{\delta \varPsi^\alpha}=\frac{\red\PD\mathcal L}{\red\PD\varPsi^\alpha}
- \sum_{\mu=0}^{3}\frac{\red\PD}{\red\PD x_\mu}\left(\frac{\red\PD\mathcal L}{\red\PD (\PD_\mu\varPsi^\alpha)}\right)=0 );
である。左辺は汎関数微分、右辺は通常の偏微分で書かれるのが正しいはず。(汎関数微分については http://homepage2.nifty.com/eman/analytic/functional.html 等を参照)
以降では は を渡る添え字、 は を渡る添え字として、その範囲は省略する。
ここで、エネルギ運動量テンソル を次のように定義すると、 (教科書でこの定義が大幅に間違っている点について本多先生から指摘があった)
(4.22)
&math( T^{\mu\nu}\equiv\red{\sum_\alpha}\,\frac{\red\PD\red{\varPsi^\alpha}}{\red\PD x_\mu}\left(\frac{\red\PD\mathcal L}{\red\PD(\PD_\nu\varPsi^\alpha)}\right)-\delta_{\mu\nu}\red{\mathcal L} );
(4.24)
&math( \sum_\nu\PD_\nu T^{\mu\nu}=&\left[\sum_{\nu,\alpha}\frac{\PD}{\PD x_\nu}\frac{\PD{\varPsi^\alpha}}{\PD x_\mu}\left(\frac{\red\PD\mathcal L}{\red\PD(\PD_\nu\varPsi^\alpha)}\right)\right]-\frac{\PD\mathcal L}{\PD x_\mu}\\ );
(4.25)
&math( \frac{\PD\mathcal L}{\PD x_\mu}=\sum_{\alpha}\left( \frac{\PD\varPsi^\alpha}{\PD x_\mu}\frac{\red\PD\mathcal L}{\red\PD\varPsi^\alpha}+ \sum_{\nu}\frac{\PD^2\varPsi^\alpha}{\PD \red{x_\mu}\PD \red{x_\nu}}\frac{\red\PD\mathcal L}{\red\PD(\PD_\nu\varPsi^\alpha)} \right) );
(4.26)
&math( \frac{\PD\mathcal L}{\PD x_\mu}&=\sum_{\alpha}\left( \frac{\PD\varPsi^\alpha}{\PD x_\mu} \sum_{\mu'}\frac{\PD}{\PD x_{\mu'}}\frac{\PD\mathcal L}{\PD(\PD_{\mu'}\varPsi^\alpha)}+ \sum_{\nu}\frac{\PD^2\varPsi^\alpha}{\PD \red{x_\mu}\PD \red{x_\nu}}\frac{\red\PD\mathcal L}{\red\PD(\PD_\nu\varPsi^\alpha)} \right)\\ &=\sum_{\nu,\alpha}\frac{\PD}{\PD x_\nu}\left(\frac{\PD\varPsi^\alpha}{\PD x_\mu}\frac{\red\PD\mathcal L}{\red\PD(\PD_\nu\varPsi^\alpha)}\right) );
より、
(4.23)
&math( \sum_\nu\PD_\nu T^{\mu\nu}=0 );
を得る。
この式を全空間で積分すれば、
(4.27A)
&math( \int d^3r\sum_\nu\PD_\nu T^{\mu\nu}&=\int d^3r\,\frac{\PD T^{\mu 0}}{\PD t}+\int d^3r\sum_i\frac{\PD}{\PD x_i} T^{\mu i}\\ &=\int d^3r\,\frac{\PD T^{\mu 0}}{\PD t}+\int d^3r\sum_i \nabla_i T^{\mu i} = 0\\ );
(4.27B)
&math( \therefore\int d^3r\,\frac{\PD T^{\mu 0}}{\PD t}=-\int d^3r\sum_i \nabla_i T^{\mu i} );
無限遠では場がないことから右辺はゼロとなり、
(4.27C)
&math( \frac{d}{d t}\int d^3r\,T^{\mu 0}=0 );
すなわちこの左辺の積分は保存量である。
(4.28A)
と置けば、これらがエネルギーおよび運動量を表す。
具体的に書き下せば、
(4.28B)
すなわち、
(4.28C)
となる。
スピン系では †
(4.28C) に (4.5) を代入すると( が に依存しないことから)、
&math( E_S&=\int d^3r\left[\dot\theta\left(\frac{\PD\mathcal L}{\PD\dot\theta}\right)+\dot\phi\left(\frac{\PD\mathcal L}{\PD\dot\phi}\right)-\mathcal L\,\right]\\ &=0+\int\frac{d^3r}{a^3}\dot\phi\hbar S(\cos\theta-1)-L_S\\ &=L_B-L_S\\ &=H_S );
&math( \bm P_S&=\int d^3r\,\left(\bm \nabla\!\theta\,\frac{\PD\mathcal L}{\PD\dot\theta}+\bm \nabla\!\phi\,\frac{\PD\mathcal L}{\PD\dot\phi}\right)\\ &=\int d^3r\,\left(0+\bm \nabla\!\phi\,\frac{\hbar S}{a^3}(\cos\theta-1)\right)\\ &=\int \frac{d^3r}{a^3}\,\hbar S\, (\bm\nabla\!\phi)(\cos\theta-1) );
(4.6) と比較すると運動量は空間方向の Berry 位相になっている(そうだ)。
4-4 局在スピンの緩和 †
(4.14) 式で見たように、スピン位置での有効磁場 がもし時間に依存しなければ、 磁場方向を向いていないスピンは永久に歳差運動を行うことになる。 しかし、実際には徐々に歳差運動が失われ、比較的速やかにスピンは磁場方向を向いて静止する。
この運動は、(4.14) にスピンの速度に比例した大きさ を持つ 「摩擦項」を加えることで記述できる。このときの比例係数 は Gilbert ダンピング定数と呼ばれ、金属磁性体の場合には 0.01 程度の大きさとなる。
(4.31)
まず、右辺から明らかに すなわち である。
したがって、右辺第2項の大きさは
と評価できる。
が小さいことから、 はほぼ に垂直であり、 方向を向く。これが歳差運動成分である。
緩和項はさらにそれに垂直であり、 方向を向く。 これがスピンを磁場方向に向ける成分である。
(4.31) から (4.32) の導出は
&math( &\dot{\bm S}=\gamma\bm B_S\times\bm S-\frac{\alpha}{S}\bm S\times\dot{\bm S}\\ &\bm S\times\dot{\bm S}=\bm S\times(\gamma\bm B_S\times\bm S)-\bm S\times\left(\frac{\alpha}{S}\bm S\times\dot{\bm S}\right)\\ &\dot{\bm S}\cdot(\bm S\times\dot{\bm S})=0=\dot{\bm S}\cdot\left\{S^2\gamma\bm B_S-(\gamma\bm B_S\cdot\bm S)\bm S\right\}+\dot{\bm S}\cdot(\alpha S\dot{\bm S})\\ &S^2\gamma\bm B_S\cdot\dot{\bm S}=-\alpha S\dot{\bm S}^2\\ &\gamma\bm B_S\cdot\dot{\bm S}=\red{\frac{1}{\hbar}}\frac{\delta H_S}{\delta \bm S}\cdot \dot{\bm S}=\red{\frac{1}{\hbar}}\frac{dH_S}{dt}=-\frac{\alpha}{S} \dot{\bm S}^2\\ &\frac{dH_S}{dt}=-\frac{\red{\hbar}\alpha}{S} \dot{\bm S}^2\\ );
途中で、 すなわち を使った。