量子力学Ⅰ/物理量の固有関数 のバックアップ(No.2)

更新

量子力学Ⅰ

概要 †

いくつかの物理量演算子の固有関数は量子力学的にも、数学的にも非常に重要な物となる。

ハミルトニアン †

演習：箱の中の自由粒子 = 実フーリエ級数 †

箱の中の自由粒子に対して、ハミルトニアンの固有関数は正弦波となることを見た。

　 \varphi_n(\bm r)=\sqrt\frac{2}{\,a\,}\sin(n\pi x/a) 　ただし　 n=1,2,3,\dots

この関数系は \varphi(0)=\varphi(a)=0 という境界条件の下で正規直交完全系を為す。

(1) n\ne m のとき、 \int_0^a\varphi_n^*(x)\varphi_m(x)dx=0 を示せ。

(2) n = m のとき、 \int_0^a\varphi_n^*(x)\varphi_m(x)dx=1 を示せ。

(3) 以下、 a=1 とする。

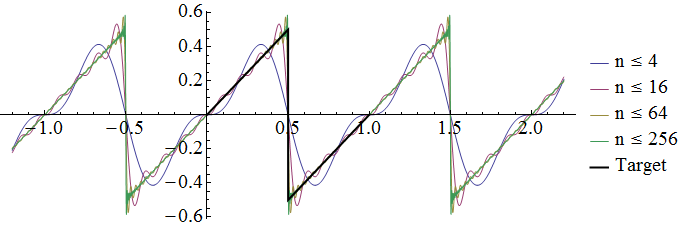
　&math(f(x)=\begin{cases} x&(0<x<1/2)\\ x-1&(1/2<x<1) \end{cases});

を f(x)=\sum_{n=0}^\infty c_n\varphi_n(x) の形に展開した際の係数 c_n を求めよ。

解説 †

(3) の関数は下図で Target として示したように x=1/2 に不連続点を持つが、 このような関数に対しても上記の無限級数は収束する。

この様子を見るために、展開係数を n=4,16,64,256 までで打ち切った場合の関数形を同じグラフに重ねて示した。

sinusoidal-expansion.png

完全な自由粒子 = 複素フーリエ変換 †

運動量の固有関数と同じになる。

運動量 = 複素フーリエ変換 †

位置 = ディラックのデルタ関数 †

角運動量 = 球面調和関数 †

質問・コメント †




Counter: 70760 (from 2010/06/03), today: 28, yesterday: 0