はじめての誤差論
目次 †
概要 †
以下は、筑波大学応用理工学類の1年生向けに開講されている 「物理学実験」という授業のオリエンテーションをかねて 1時間目に学ぶ「誤差論」の部分の教科書原稿です。
歴代の担当者が少しずつ手直ししてきた内容で、 最新版(2014年度時点)はかなりの部分に武内の手が入っています。
物理学実験では確率密度分布や正規分布などを習ったことのない学生向けに 1.5〜2コマ程度で誤差論の概観を把握してもらおうという少し無茶な カリキュラムで教えているのですが、 2年生以降の学生さんが復習するにはちょうど良いかもしれませんので ここに上げておこうと思います。
誤差論 †
長さ、時間、温度など、どんな物理量を測定する場合でも、種々の要因によって測定には不確かさが含まれ、
測定値は真の値に一致しない。この測定値と
(1)
また、誤差と真値との比を相対誤差と呼び、単位の異なる物理量の不確かさを比較したり、乗除算による誤差の
(2)
相対誤差との混同を避けるため、式1で定義される誤差を絶対誤差と呼ぶこともある。
測定値に含まれる誤差の大きさを正しく見積もることは大変重要である。しかし、実際には真の値は分からないから、正確な誤差の大きさも分からない。そこで、誤差を評価するには測定値から真の値を推定し、また、誤差の大きさを推定することになる。
測定値の表し方 †
誤差を評価した後の測定結果は、真値の推定値 と誤差の推定値 を用いて
(3)
のように表す。たとえば、真値の推定値が 27.32、誤差の推定値が 0.02 であれば、
(4)
となる。これを などと書いてしまうと、どの桁に誤差が含まれるかが分かりにくいため、真値と誤差の推定値は表示桁をあわせるべきである。
表示桁を合わせて書けば明らかなように、誤差の推定値に要求される精度は有効数字+1桁〜2桁もあれば十分であり、数桁も求めても無意味である。
測定誤差とその原因 †
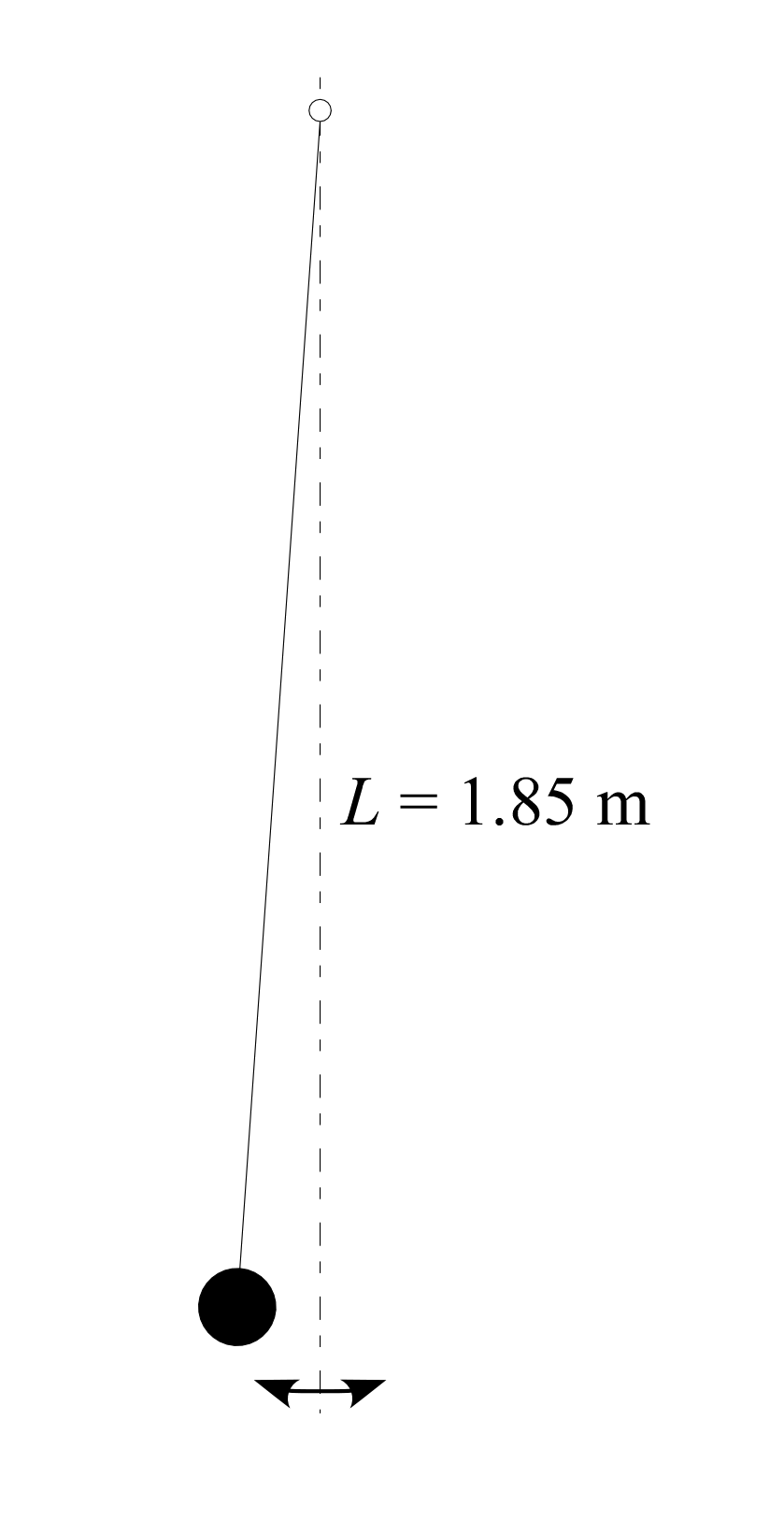
測定誤差はどのような原因によって生じるであろうか。振り子の周期 から重力加速度 を求める実験を例にとって、測定値に含まれる誤差の原因について考えてみよう。
長さ の振り子を、初期角 から振動させる。おもりが最初に最下点を通過したときから測定を始めて、10回振動するのにかかる時間(振動周期の10倍)を、100分の1秒まで測れるストップウォッチで 50 回測定した。得られたデータは次の通りである。(単位は秒)
| 27.26 | 26.99 | 27.06 | 27.18 | 27.25 | 27.27 | 27.34 | 27.27 | 27.22 | 27.25 |
| 27.26 | 27.18 | 27.41 | 27.31 | 27.28 | 27.27 | 27.26 | 27.24 | 27.26 | 27.27 |
| 27.21 | 27.22 | 27.24 | 27.26 | 27.27 | 27.27 | 27.57 | 27.34 | 27.38 | 27.28 |
| 27.27 | 27.44 | 27.35 | 27.28 | 27.18 | 27.22 | 27.26 | 27.37 | 27.24 | 27.43 |
| 27.18 | 27.27 | 27.31 | 27.38 | 27.25 | 27.18 | 27.29 | 27.38 | 27.31 | 27.35 |
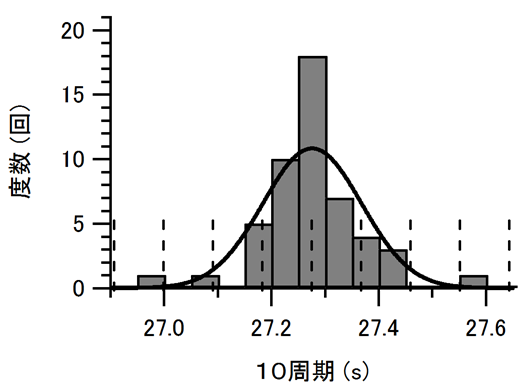
50個の測定値を平均すると27.28秒となるが、個々の測定値は平均値の周りにランダムに分布している。この分布を調べるため、以下にヒストグラムを示した。
ヒストグラムは、日本語で
ヒストグラムによれば、測定値は平均値27.28秒の近くの に集中しており、平均値から離れるに従って度数が減る。平均値のまわりで測定値がばらつくのは、さまざまな誤差が影響しているためである。また一般に、この平均値自体も真の値と完全には一致しない。
誤差の原因として、以下のようなものが考えられる。次にそれぞれを詳細に検討してみよう。
- 初期角が一定でなかった・精確でなかった
- 空気や支点での抵抗により周期が変化した
- ストップウォッチが不正確
- 振動回数の数え間違い
- ストップウォッチを押すときの癖、またはランダムなずれ
原因 1. についての検討 †
一般に振り子の振動周期は初期角(振幅)に依らないとされるが、これは振幅が小さいという仮定を用いた単振動近似の結果である。単振動近似を用いない正確な物理モデルを使うことで、初期角がわずかに異なった際に周期がどれだけ変化するかを数値計算で求められる。 の時の結果を以下に示す。
| 初期角(度) | 10 | 5 | 4 | 3 | 2 | 1 | 0.5 |
| 周期(s) | 2.7352 | 2.7312 | 2.7308 | 2.7304 | 2.7301 | 2.7300 | 2.7300 |
この結果によれば、初期角が を中心に の範囲で変化しても、10周期にかかる時間の違いは100分の1秒以下であり、測定結果のばらつきの原因とは考えられない。
原因 2. についての検討 †
空気抵抗や支点における抵抗を考慮して理論式を解くことができる。抵抗により振幅が減衰し、初期の半分になるまでにかかる時間を とすると、初期角が小さい場合の周期は を減衰定数として、
(5)
となる。ただし、右辺は が に比べて小さいことを仮定して近似した結果である。たとえば、抵抗を大きく見積もって を60秒としても、 に対して、 であるから、 は に比べて1万分の1以下である。したがって、周期を有効数字4桁で測定している場合、 が60秒程度かそれ以上であれば、周期に対する抵抗の影響は無視できる。
原因 3. についての検討 †
一般にはストップウォッチは測定に十分な精度を持つと考えられる。しかし、測定結果がどうしても説明できない場合は本当に正確かどうか調べる必要が出てくる。
原因 4. についての検討 †
周期がおおよそ2.7秒なので、半周期分間違うと誤差は1.4秒程度になる。先の測定例では数え間違いは無いと考えられる。
原因 5. についての検討 †
人間が振り子を目で見てストップウォッチを押す場合、この種の誤差は避けられない。この種の誤差を減らすためには、測定に熟達するか、あるいは測定手段自体を改良する必要がある。
誤差の分類 †
上で見たような各種の誤差は、系統誤差と偶発誤差の2つに大別できる。
系統誤差 †
すべての測定結果に決まった関係で導入される誤差で、繰り返し測定を行えば毎回同じ値の誤差を生じる。系統誤差は、例えば次のような要因によって生じうる。
- 理論(モデル)の誤り(理論誤差)
- 測定器固有の特性(機械誤差)
- 測定者の一定の癖(個人誤差)
上記の例では、原因 1. と関連して振り子を理想的な調和振動子として扱っている点や、原因 2. で抵抗を無視している点が理論誤差であり、原因 3. による誤差が機械誤差、原因 4. の癖に関する部分が個人誤差に相当する。そのほか、振り子の釣り紐の重さを無視していることなども理論誤差である。
系統誤差は測定値をばらつかせるのではなく、平均値をずらす形で測定に影響を与えるため、測定結果から誤差の存在に気づくのが困難な場合が多く、その大きさを評価することも難しい。しかし、誤差の原因が分かれば、測定や解析を改良する事で誤差を避けたり、後で補正することで誤差を完全に取り除くことができる場合もある。
偶発誤差(偶然誤差ともいう) †
偶発的な原因によって測定結果に導入される誤差で、繰り返し測定を行えば毎回異なる値の誤差を生じる。偶発誤差は、次のような要因によって生じる。
- 測定者の過失(過失誤差)
- 測定者のランダムな測定むら、測定器の精度限界(読み取り誤差、必然的偶発誤差)
上記の例では、原因 4. による誤差が過失誤差、原因 5. による誤差が必然的偶発誤差に相当する。
偶発誤差は、系統誤差とは異なり、後から理論的に補正することができないものの、測定を繰り返した際に測定値のばらつきとして目に見える形で現れるため発見が容易であり、以下に示すように統計的な処理を行うことで大きさを評価したり、誤差を小さくすることが可能である。
系統誤差は測定対象や測定環境ごとに個々に検討する必要があり、統一した理論により扱うことが難しいのに対して、偶発誤差についてはそれを扱う統一的な手法が確立されている。
以下、偶発誤差のみ考える †
以下では系統誤差が十分に小さいか、あるいは何らかの方法ですでに取り除かれており、主に必然的偶発誤差が測定精度を決めている場合を考える。また、誤差とは必然的偶発誤差を意味するものとする。
誤差の分布(確率分布) †
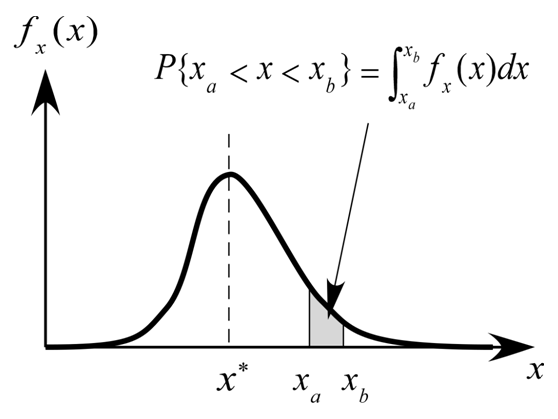
誤差を含む測定では、測定値 は測定ごとに異なる値を取る。誤差論では、この測定値 が、ある確率分布 を持つと仮定する。
確率分布 の意味するところは、一回の測定で が の範囲に入る確率 を、
(6)
として求められるということである。
上図に確率分布の例を示した。多くの場合、 は真値 の周りで大きな値を取り、離れるにしたがって小さくなる。上の定義により、測定値が のある範囲(ここでは )に入る確率は、図のように で定義される面積に等しい。したがって、 が真値の周りで大きな値を取ることは、測定において真値に近い が得られる確率が、真値から遠い が得られる確率に比べて高いことを示している。
の形は測定対象により様々であるが、測定を行えば必ず何らかの値が得られることから、 を全範囲にわたって積分した値は常に1になる。
(7)
また、 の期待値 は次の形で定義される。*1このようにして定義された期待値は、仮想的に測定を無限回繰り返したときに得られる平均値に相当する
(8)
以下では は真値 の周りで平均的に分布しており が と一致する場合を考える。測定条件の設定に誤差が含まれたり、系統誤差が無視できない場合を除いて、妥当な仮定である。
(9)
測定誤差の大きさは の標準偏差 で評価することができる。
(10)
が大きければ真値 から離れた が測定される確率が高く、測定誤差が大きいことになる。
標準偏差がどうしてこのような形で定義されるかに興味のある学生は、 「測定値の真値からのずれ」の期待値を単純に求めてしまうと、
のようにゼロになってしまうことに注意せよ。
期待値がゼロにならないように「ずれの期待値」を定義する方法としては、
のように「ずれの絶対値の期待値」を評価する方法もあるが、「ずれの2乗の期待値」を
として分散と呼び、その平方根を上記のように標準偏差とした方が数学的に扱いやすく、 さまざまな発展がある。このあたりは統計学の教科書を参考にすること。
測定値の統計処理 †
ある測定を行うにあたって、測定値の確率分布 は未知であるから、測定精度を高め、また誤差を評価するためには、同じ測定を多数回行い、それらの値から統計処理によって や を推定することになる。ここでは、 回の測定で測定値 が得られたとしよう。
このとき、真値 の最良推定値は測定値 の平均値 で与えられる。
(11)
測定値 の分散 および標準偏差 は以下のように定義される。
(12)
(13)
の標準偏差 と測定値 の標準偏差 とを区別して考える必要がある。一般に、 が十分に大きいとき、 は に近い値が得られることが期待される。しかし、 が有限の時、 の最良推定値は ではない。正しい推定値は以下の形で与えられる。証明は → はじめての誤差論/真値と標準偏差の推定
(14)
中心極限定理 †
式11から真値を、式14から確率分布の標準偏差を推定する事ができた。多数回の測定から推定した は、個々の測定で得られる に比べ、より真値 に近い値であることが期待される。しかし、いくら測定回数を増やしても誤差をゼロにする事はできない。つまり、平均値 自体もある確率分布 に従う。では、 に含まれる誤差はどのように推定すればよいだろうか?
中心極限定理によれば、測定回数 が大きいとき、 の確率分布 は元の確率分布 の形によらず、
(15)
の形に近づく。この右辺はガウス関数(ガウシアン)、あるいは正規分布関数と呼ばれ、この分布を正規分布と呼ぶ(式の上ではごちゃごちゃしていて、とても難しそうに見えるのだが、 を縦横に引き延ばしたり縮めたりずらしたりしただけのものなので恐れないように)。 は の期待値であるが、 の期待値も同じ値となる。一方、 は の標準偏差を与えるが、これは の標準偏差 を用いて
(16)
と表せる。すなわち、 は と同じ値を中心として、 の幅を持つ関数となる。確率分布関数の幅が狭くなることは誤差が小さくなることを表すから、 回の測定の平均値を取ることで、偶発誤差を1回の測定の にできると覚えると良い。
標準誤差 †
式14と式16より、多数回の測定から式11を使って求めた平均値 に含まれる誤差は、
(17)
と推定でき、測定結果を式3にならって次のように書ける。
(18)
推定した測定誤差を を用いて表すとき、これを標準誤差と呼ぶ。先の振り子の測定例では、 、 、 であるから、標準誤差 となる。
(19)
別の表記法として、
(20)
という表し方もよく用いられる。
誤差推定の意味 †
ここまで「誤差の推定値」という言葉を正確に定義せずに用いてきた。正規分布では期待値からどんなにかけ離れた値を取る確率もゼロではない。つまり、運が悪ければ極端に真値からかけ離れた値が得られることもある。つまり「誤差の最大値」は存在しない。一方で、測定値の周りにある幅を持った領域を取れば、真値がその範囲に入る確率を予想する事ができる。正規分布は、
(21)
となる性質があるため、得られた推定値 が真値 の周りの の範囲に入る確率、つまり、実際の誤差が より小さくなる確率は約 68.3% でしかない。逆に言えば、31.7% の確率で、実際の誤差はこれより大きくなる。
範囲をこれより広く取り、平均値から や の範囲を考えれば、測定点が範囲に入る確率が高くなる。正規分布で値が $\pm 2\sigma$、$\pm 3\sigma$ に入る確率はそれぞれ約95.5%、約99.7%の確率である。目的によっては、誤差の推定方法を明記した上で測定誤差を や で表すことも行われる。
このように、測定データに付けられた誤差範囲は、必ずその範囲に真の値があると主張するものではない。あくまで統計的に誤差の大きさを評価した物である事を覚えておく必要がある。また、上記の 68.3% などという値は $\bar x$ が分散 を持つ正規分布と見なせる場合の話であり、正確な検定等をする場合には、サンプル数が有限であることや $\sigma_{\bar x}'$ が $\sigma_{\bar x}^\ast$ の推定値でしかないことなどを考慮する必要がある。詳しくは別途、区間推定や検定に関して学んで欲しい。
間接測定量の測定精度 †
長さや時間のように、直接測定できる物理量を直接測定量という。対して、直接測定量の関数として求められる量を間接測定量という。上の例では、振り子の長さ、重さ、10周期などが直接測定量であり、それらの値を使って計算で求める重力加速度や1周期が間接測定量である。後述の誤差
振り子の振幅が小さいときに成り立つ関係式
(22)
より、
(23)
と書ける。このとき、誤差伝播の式(付録の式E.4)から、最大誤差を次の形で書ける。
(24)
数学では は定数で誤差はないが、実際の計算では無理数 をある実数で近似するため、丸め誤差 が生じてしまう。
それでは、重力加速度 が か かを区別するためには、 , , にどの程度の精度が必要であろうか。この2つの値を実験的に区別するには、およそ とする必要がある。式14の右辺に出てくる誤差はそれぞれ独立だから、少なくとも右辺の各項を 0.001 よりも小さくする必要がある。この条件は、それぞれ以下の制限を与える。
(25)
(26)
(27)
したがって、 については 3.14 としたのでは不十分であり、少なくとも 3.1416 として計算する必要がある。また、振り子の長さ については 1 mm 程度の精度で測定しなければならない。周期 については、先の測定例における標準誤差は 0.0013 (s) であるから、上記の精度を満足している。しかし、もし測定回数が10回であるとしたら、標準誤差が 0.0029 (s) となり、精度が足りない。
有効数字 †
測定で得られた数値は誤差を伴っているから、値をノートに書き留める際や、その値を用いて計算を行う場合には有効数字に注意を払う必要がある。
加減算の場合 †
加減算の場合は絶対誤差が問題になる。例えば、高さ (物差しで計測)の台の上に、厚みが (ノギスで計測)の鉄板を載せ、さらにその上に高さが (マイクロメーターで計測)の物体を立てた時の合計の高さを求める場合を考える。
(28)
この場合、読み取り精度の低い 30.1 や 12.25 の表示されていない下位桁(小数点以下第2、第3位)は、ゼロが入っているのではなく、その桁の値は分からないのであるから、左側の様に計算しても意味がない。そこで、右側に示したように他の数値を四捨五入した上で小数点以下2桁まで取って計算を行い、最後に四捨五入して最も精度の低い値に合わせて小数点以下1桁にするのが正しい計算方法である。
加減算では計算の前後で有効桁数が変化しうる。例えば、4.148 と 8.412 を加えれば 12.560 で、有効桁数は4から5へ増加する。一方で、1.423 から 1.389 を引けば 0.034 で、有効桁数は4から2へ激減する。後者のように、絶対値のほとんど等しい2つの数値の加減算により、有効桁数が減少してしまうことを
複雑な数値計算を行う際には、計算順序を工夫するなど桁落ちによる精度の低下を防ぐ手立てを講じなければならない場面が多く存在し、長年の研究によりノウハウが蓄積されている。特に数値計算で行列演算を行う場合には、線形代数の教科書にあるような手順をそのままプログラムにしたのでは桁落ちのために誤差の大きな結果が得られてしまう危険がある。実績のある数値演算ライブラリを、その特性を理解した上で用いることが必要となる。
乗除算の場合 †
乗除算の場合は、次の誤差の伝播で詳しく述べるように、各測定値に対する測定精度の割合、つまり、相対誤差が問題になる。有効桁数は相対誤差の概算値を与えるため、簡単には最も小さな有効桁数に合わせて計算結果を四捨五入することで、正しい取り扱いができる。
例えば、質量 102.456 gで、縦、横、長さがそれぞれ 14.15 mm, 10.264 mm, 70.2 mm の棒の密度を求める場合を考える。質量、縦、横、長さの数値の有効数字はそれぞれ、6桁、4桁、5桁、3桁である(小数点以下の桁数と混同しないこと)。この場合、最も小さい有効数字は3桁であるから、有効数字が3桁より大きい数値については四捨五入して3桁より1桁多い4桁にして計算を行い、最後に四捨五入して有効数字3桁の密度を得る。
(29)
有効数字と相対誤差 †
有効数字2桁の数値の相対誤差は何%であるか?
は を有効数字2桁で評価した物であるが、これは であることを示しているから、相対誤差は であると言える。
一方、 はやはり を有効数字2桁で評価した物であるが、これは であることを示しているから、相対誤差は である。
このように同じ有効数字2桁の数値でも、最上位の桁が 1 に近い場合と 9 に近い場合とで相対誤差は大きく異なる。有効数字はあくまで相対誤差をおおざっぱに評価する目安にしかならないため、その有効性を過信してはならない。
誤差の伝播 †
長さや時間のように直接測定できる物理量を直接測定量という。一方、直接測定量の関数として求められる量を間接測定量という。直接測定量の誤差が間接測定量に誤差を生じることを示して誤差の伝播という。いま、間接測定量 が直接測定量 の関数として、
(30)
のように表されているとする。 の誤差 が十分小さい場合には、 を真値のまわりで Taylor 展開し、2次以上の項を無視する事により、 の誤差 は次の様に表せる。
(31)
一般の場合 †
上式から、
(32)
が常に成り立つので、この式の右辺から間接測定量 の最大誤差を見積もる事ができる。
特に、
が
のように直接測定量の
(33)
この式で、各項に含まれる などの形は相対誤差を表しており、乗除算の誤差伝播に相対誤差による評価、あるいは簡単には有効数字による評価が適している事が分かる。
全ての直接測定量の誤差が偶然誤差である場合 †
この場合、 などのように、異なる誤差の積の期待値はゼロになる。従って、誤差の二乗の期待値を求めることによって、次式が得られる。
(34)
ここで、 は、各物理量の標準誤差である。特に、 が のように直接測定量の冪乗の積の形で表される場合には、この両辺を で割ることにより、次の式が得られる。
(35)
このように、すべての誤差を偶発誤差であると仮定すれば、間接測定値の偶発誤差を最大値ではなく期待値で評価することが可能である。
質問・コメント †
"最良推定値" †
()
"最良推定値"の"最良"には語弊があると思いました。
相対誤差幅について †
学生? ()
加減算で測定値が桁落ちし、有効数字が1桁になったのですがこの値を乗除算に使うときは、最終的に計算結果は、有効数字1桁の値にすれば良いのですか?
- もし途中で1桁になってしまったのであれば最終結果の有効数字も1桁とせざるを得ないですが、現実の問題ではそれで「良い」かと言われればダメな場合が多いでしょうね。測定方法や計算方法を工夫して精度を上げられないか検討することが必要なのではないかと思います。 -- 武内(管理人)?
すべての誤差を正規分布に従う偶発誤差であると仮定すれば、について †
otnotskt? ()
また, 「すべての誤差を正規分布に従う偶発誤差であると仮定すれば、間接測定値の偶発誤差を最大値ではなく期待値で評価することが可能である」とのことですが, 「正規分布」は不要ではないでしょうか...?
「有効数字はあくまで相対誤差をおおざっぱに評価する目安にしかならないため、その有効性を過信してはならない」というのはまさしくその通りと思い, 意を強くしました。ありがとうございます。
- おっしゃる通りですね。「正規分布」の語を削除しました。 -- 武内(管理人)?
x=1.0は0.95<x<1.05であることを示している, について †
otnotskt? ()
有効数字について, x=1.0は0.95<x<1.05であることを示している, とのことですが, 1.0は「四捨五入して1.0になる量」と, 「1.0を中心として不確かさが0.1のオーダーである量」という2通りの解釈ができ, 前者ならたしかに0.95<x<1.05ですが, 後者なら0.90<x<1.10であっても0.80<x<1.20であってもxは有効数字で表すなら1.0になるのではないでしょうか...? 多くの誤差論や物理学実験のテキストは前者が前提のようで, 後者については考えられていないように思うのですが, 誤差を含んだデータの扱いでは、後者もありえると思うのです。以前からちょっと疑問に思っております。ご教示頂けますと幸いです。
- コメントありがとうございます。丸め誤差が主な誤差なら 0.95 < x < 1.05 だが、その他の誤差が主である場合には「不確かさが0.1のオーダー」という程度の意味しか持たない。また、測定値に関しては丸め誤差が主でも、それを使って有効数字を使った大雑把な誤差評価のまま間接測定量を求めれば、その結果についてはやはり「不確かさが0.1のオーダー」という程度の意味しか持たない。確かにその通りだと思います。どう改定するか考えることにいたします。 -- 武内(管理人)?
誤差伝搬について †
yuki? ()
武内様
記事拝見させていただきました。ありがとうございます。
誤差伝搬に関して2点質問させていただきます。
(質問1)
直接測定で得られた測定値の平均をm、誤差を1σとした場合、推測される母平均μは68 %の確率で(m-σ)<=μ<=(m+σ)に存在すると思います。また、複数の直接測定で得られた誤差1σの測定値から求まる間接測定値の誤差は誤差伝搬で求められると思います。
ここで本題の質問ですが、間接測定値の平均をm'とし誤差伝搬で求めた誤差をeとした場合、母平均μ'は68 %の確率で(m'-e)<=μ'<=(m'+e)に存在するとみてよろしいのでしょうか?
(質問2)
また、例えばt分布で間接測定値の誤差を95 %信頼区間とした場合の値としたとき、間接測定値の平均をm'とし誤差伝搬で求めた誤差をeとした場合、母平均μ'は95 %の確率で(m'-e)<=μ'<=(m'+e)に存在するとみてよろしいのでしょうか?
お時間があればご回答よろしくお願い致します。
無題 †
()
レポートの参考にさせていただきました。
匿名が多いネットの中で実名でやってらっしゃる方の情報は信頼できるので助かります。
ありがとうございます。
お世話になりました、ご多忙中に失礼。 †
中平 耕一郎? ()
測量誤差の処理法 やっと一通り目を通しました、
パラパラとですが、なんでこんなに難しいの、
高校の時確率統計をさぼった罰かなと、
思いましたが、”今回これが成り立つことは証明しないが”、
なので、言葉を覚えて登場人物が増えていくみたいですが、
読み進んでもいいよまだ入門だから、ということで、
読み進むことはしました、読み直すべきか、次の本に進むか悩んでいます。
初めての誤差論 †
中平 耕一郎? ()
ご多忙中に失礼します。
”初めての誤差論”見ました、誤差論について何かいい本を紹介お願いできないでしょうか。
当方、確率・統計はほとんど覚えていませんので、
高校程度の確率統計
大学での、確率統計
そして、誤差論
について何冊でもいいので、ご紹介切望しております。
- コメントありがとうございます。
あまり多くの本に目を通しているわけではないため、自信を持ってお勧めできるわけでもないのですが、私の知っている本ということで以下を挙げさせていただきます。
「確率統計」の専門書を読もうとすると、始めに出てくる「確率変数」の定義からすでに素人を寄せ付けない印象で、数学的な厳密さを求めて書かれた物は特に読みづらいのではないかと思います。 そのように取っつきにくい確率論の初歩について、数学的な厳密性をできるかぎり排除せず、しかも分かりやすく説明している本として 「数学ガール(乱択アルゴリズム)」 があります。 その気になれば高校生でも楽しんで読めるように書かれていて、確率変数や標本空間、確率分布について一通りのことを学べます。
誤差や検定については、東大出版会の 「自然科学の統計学」 が詳しいです。同じシリーズで 「統計学入門 (基礎統計学) 」 もあります。この2冊を理解した暁にはデータ解析の専門家になれそうなくらいの分量がありますので、必要な部分を選んで学ぶような使い方になるのかもしれません。
参考になれば幸いです。-- 武内(管理人)? - ありがとうございました -- 中平 耕一郎?
- ありがとうございました。あれから -- 中平 耕一郎?
- 日本測量協会の測量誤差の処理法読みました。誤差論への違和感が和らいだ感じがあります -- 中平耕一郎ご多忙中を失礼します?
添付ファイル: