スピントロニクス理論の基礎/5-3

更新

[前の章へ] <<<<　 スピントロニクス理論の基礎（目次）　>>>> [次の章へ]

5-3 ゼロモード†

(5.12) 式の固有値方程式から得た (5.13), (5.15) の固有関数を用いて ゆらぎ \tilde\eta を展開し、その係数を \eta_i とする。

(5.18)

\tilde\eta(\bm r,t)=\frac{1}{2}\eta_0(t)\varphi_0(z)+\sum_k\eta_k(t)\varphi_k(z)

これを (5.11) に代入すると、ラグランジアンを \eta_i を変数として表せる。

(5.11)

L_S=-\hbar S\int\frac{d^3r}{a^3}\left(\bar{\tilde\eta}\dot{\tilde\eta}-\dot{\bar{\tilde\eta}}\tilde\eta\right)-2KS^2\left\{\lambda^2\nabla\bar{\tilde\eta}\nabla\tilde\eta+\left(1-\frac{2}{\cosh^2 u}\right)\tilde{\bar\eta}\tilde\eta\right\}\\

を、

&\int \frac{d^3r}{a^3} \bar{\tilde\eta}\dot{\tilde\eta}\\ &=\frac{A}{a^3}\int dz \left(\frac{1}{2}\bar\eta_0(t)\bar\varphi_0(z)+\sum_k\bar\eta_k(t)\bar\varphi_k(z)\right) \left(\frac{1}{2}\dot\eta_0(t)\varphi_0(z)+\sum_k\dot\eta_k(t)\varphi_k(z)\right)\\ &=\frac{A}{a^3}\left(2\lambda\bar\eta_0\dot\eta_0+\sum_{k',k}\bar\eta_{k'}\dot\eta_k\delta(k'-k)\right)

&\int \frac{d^3r}{a^3}\left\{\lambda^2\nabla\bar{\tilde\eta}\nabla\tilde\eta+\left(1-\frac{2}{\cosh^2 u}\right)\bar{\tilde\eta}\tilde\eta\right\}\\ &=\frac{A}{a^3}\int dz\left\{\lambda^2\nabla_z\bar{\tilde\eta}\nabla_z\tilde\eta+\left(1-\frac{2}{\cosh^2 u}\right)\bar{\tilde\eta}\tilde\eta\right\}\\ &=\frac{A}{a^3}\int dz\left\{-\lambda^2\bar{\tilde\eta}\nabla_z^2\tilde\eta+\left(1-\frac{2}{\cosh^2 u}\right)\bar{\tilde\eta}\tilde\eta\right\}\\ &=\frac{A}{a^3}\int dz \bar{\tilde\eta}\left\{-\lambda^2\nabla_z^2+\left(1-\frac{2}{\cosh^2 u}\right)\right\}\tilde\eta\\ &=\frac{A}{a^3}\int dz \left(\frac{1}{2}\bar\eta_0(t)\bar\varphi_0(z)+\sum_k\bar\eta_k(t)\bar\varphi_k(z)\right) \left(\frac{0}{2}\eta_0(t)\varphi_0(z)+\sum_k\omega_k\eta_k(t)\varphi_k(z)\right)\\ &=\frac{A}{a^3} \sum_{k',k}\omega_k\bar\eta_{{k'}}\eta_k{\delta(k'-k)}\\

などに注意して展開すると、

(5.19)

L_S=N_w\left[\frac{i\hbar S}{4}(\bar\eta_0\dot\eta_0-\dot{\bar\eta}_0\eta_0)+ \red{\frac{1}{2\lambda}}\sum_{\red{k'},k}\big\{i\hbar S(\bar\eta_{\red{k'}}\dot\eta_k-\dot{\bar\eta}_{\red{k'}}\eta_k)-2KS^2\omega_k\bar\eta_{\red{k'}}\eta_k\big\}\red{\delta(k'-k)}\right]

となる気がする？ただし、 N_w\equiv 2\lambda A/a^3 は (5.8) ですでに出てきたがここで初めて定義される定数で、磁壁を構成しているスピンの総数である（ A は系の断面積）

N_w に含まれる 2\lambda は \varphi_0 が正規化されていなかったために現れた定数なので、正規化されてた \varphi_k からは出てこない。そのため全体を N_w で括ると上記の \red{1/2\lambda} が現れてしまう。

そもそも、(5.14) から (5.17) あたりでは k は連続だったのに、 (5.18) の展開で k を整数に限っているのがおかしい。 \delta(k'-k) は次元を持つので、これを無視してしまうと次元すら狂ってしまう。

(5.18)'

\tilde\eta(\bm r,t)=\frac{1}{2}\eta_0(t)\varphi_0(z)+\red{2\lambda\int dk}\eta_k(t)\varphi_k(z)

とすれば、

(5.19)'

L_S=N_w\left[\frac{i\hbar S}{4}(\bar\eta_0\dot\eta_0-\dot{\bar\eta}_0\eta_0)+ \red{2\lambda\int dk}\big\{i\hbar S(\bar\eta_k\dot\eta_k-\dot{\bar\eta}_k\eta_k)-2KS^2\omega_k|\eta_k|^2\big\}\right]

となって、これなら次元も問題ない。

ただ、これ以降の話が全部 \sum_k で書かれているので、 果たして上記の解釈が正しいのかどうか、あまり自信を持てない・・・

スピン・スピン相互作用はどこへ行ったのか？†

(5.19)' を見ると、スピン・スピン相互作用を表す J が顕わに現れず、 一見すると、容易軸異方性 K だけで書けているように見えてしまう。

ではスピン・スピン相互作用がまったく効いていないのかというと そう言うわけではなくて、教科書で落ちていた、積分に掛かる \red{2\lambda} の部分、および、 \omega_k に含まれる \lambda 経由で J の効果が現れる。

特に、 \lambda K=\sqrt{JK} なので、 K と J は同じくらい含まれていると言って良いのかもしれない。

θとの関係†

(5.4) に (5.18)' を代入すると、

(5.20)

&\xi=\exp\left\{-u+i\phi_0+2\cosh u\left[\frac{1}{2}\eta_0\varphi_0+\red{2\lambda\int dk}\eta_k\varphi_k\right]\right\}\\ &\red{=}\exp\left\{-\frac{z-X}{\lambda}+i\phi_0+\eta_0+2\cosh u\left[\red{2\lambda\int dk}\eta_k\varphi_k\right]\right\}\\ &\red{=}\exp\left\{-\frac{z-(X+\lambda\mathrm{Re}[\eta_0])}{\lambda}+i(\phi_0+\mathrm{Im}[\eta_0])+2\cosh u\ \red{2\lambda\int dk}\eta_k\varphi_k\right\}\\

となって、普通に (5.20) が得られそうに思うのだが、 教科書では何故か等号が \simeq になっている。 どこかに近似が入っている？？？

(5.20) から、 \varphi_0 の励起モードは、 係数 \eta_0 の実部が X を、虚部が \phi_0 を、 それぞれシフトすることに対応している。

(5.21)

X(t)=X+\lambda\mathrm{Re}\eta_0(t)

\phi_0(t)=\phi_0+\mathrm{Im}\eta_0(t)

ゼロモードの存在により、これら X(t) および \phi_0(t) 自体が力学変数に昇格することになる。

励起モードの直交性 (5.16) により、ラグランジアンはこれら X(t), \phi_0(t) による部分と、それ以外の励起モード \eta_k による部分とに分離できる。

\eta_0=\frac{X(t)-X}{\lambda}+i\left(\phi_0(t)-\phi_0\right)

&\bar\eta_0\dot\eta_0-\dot{\bar\eta}_0\eta_0\\ &= \left\{\frac{X(t)-X}{\lambda}-i\left(\phi_0(t)-\phi_0\right)\right\} \left\{\frac{\dot X(t)}{\lambda}+i\dot\phi_0(t)\right\} - \left\{\frac{\dot X(t)}{\lambda}-i\dot\phi_0(t)\right\} \left\{\frac{X(t)-X}{\lambda}+i\left(\phi_0(t)-\phi_0\right)\right\}\\ &= \left\{\frac{X(t)}{\lambda}-i\phi_0(t)\right\} \left\{\frac{\dot X(t)}{\lambda}+i\dot\phi_0(t)\right\} - \left\{\frac{\dot X(t)}{\lambda}-i\dot\phi_0(t)\right\} \left\{\frac{X(t)}{\lambda}+i\phi_0(t)\right\}\\ &=\frac{2i}{\lambda}\left\{X(t)\dot\phi_0(t)-\dot X(t)\phi_0(t)\right\}

途中で時間に対する全微分となる項 ( 定数×時間微分 となる項) は落とした。

(5.23)

L_w^{(0)}=\frac{\hbar N_wS}{2\lambda}(\dot X\phi_0-X\dot\phi_0)

L_{sw}=\red{2\lambda}N_w\red{\int dk}\big\{i\hbar S(\bar\eta_k\dot\eta_k-\dot{\bar\eta}_k\eta_k)-2KS^2\omega_k\bar|\eta_k|^2\big\}

以上の結果から、磁壁の位置 X と回転位相 \phi_0 は力学変数として振る舞うことが裏付けられた。これらの変数は「集団座標」である。

これらを含んだ形で書くと、5-2 で見た関係式は

(5.25)

\cos\theta=\tanh\frac{z-X(t)}{\lambda}

\sin\theta=\frac{1}{\cosh\frac{z-X(t)}{\lambda}}

\phi=\phi_0(t)

と表せる。

量子論†

経路積分の復習 を参照。

ラグランジアンを (5.26) のように経路積分の位相に直す際、 上記リンク先では \exp \frac{i}{\red \hbar}\int dt \mathcal L とされていたが、 教科書では \red{1/\hbar} の係数がない。

このあたりの流儀はまだよく分かっていないが、 L がエネルギーの次元を持っていることを考えると、 1/\hbar は恐らく必須。

(5.26) から (5.27) へのくだりは個人的な勉強不足でついて行けてないのだが、 この部分ではとりあえず飛ばしていっても何とかなりそう？ （基本的な量子力学を復習し直さないと・・・）

外部磁場の効果†

(5.23) から運動方程式を求めると、

\frac{d}{dt}\left(\frac{\PD L_S}{\PD \dot X}\right)=\frac{\PD L_S}{\PD X}

\dot \phi_0=-\dot \phi_0

\dot \phi_0=0

そして、

\frac{d}{dt}\left(\frac{\PD L_S}{\PD \dot \phi_0}\right)=\frac{\PD L_S}{\PD \phi_0}

-\dot X=\dot X

\dot X=0

となって、何ら意味のある解は得られない。

例えばこの系の容易軸方向( z 軸方向)に外部磁場がかかると状況は変化し、 外力により磁壁が駆動される。

ただしそのようにスピンが運動する状況を記述するには、 (4.33) で導入した運動方程式の「緩和項」を考慮しなければならない。

(4.33) の緩和項を変数変換すると、(5.25) より \frac{d}{dt}\sin\theta=\dot\theta\cos\theta=-\frac{\dot X\sinh\frac{z-X}{\lambda}}{\lambda\cosh^2\frac{z-X}{\lambda}} =-\frac{\dot X}{\lambda}\cos\theta\sin\theta

\dot\theta=-\frac{\dot X}{\lambda}\sin\theta

\dot\phi=\dot\phi_0

(5.28)

&W_S=\int\frac{d^3r}{a^3}\frac{\hbar\alpha}{2S}\dot{\bm S^2}\\ &=\frac{\hbar SA\alpha}{2a^2}\int\frac{dz}{a} (\dot\theta^2+\sin^2\theta\dot\phi^2)\\ &=\frac{\hbar SA\alpha}{2a^2}\int\frac{dz}{a} \sin^2\theta\left(\frac{\dot X^2}{\lambda^2}+\dot\phi_0^2\right)\\ &=\frac{\hbar SA\alpha}{2a^2}\left(\frac{\dot X^2}{\lambda^2}+\dot\phi_0^2\right)\int\frac{dz}{a} \frac{1}{\cosh^2\frac{z-X}{\lambda}}\\ &=\frac{\hbar SA\alpha}{2a^2}\left(\frac{\dot X^2}{\lambda^2}+\dot\phi_0^2\right)(2\lambda)\\ &=\frac{\hbar S\alpha}{2}\left(\frac{\dot X^2}{\lambda^2}+\dot\phi_0^2\right)N_w\\

閑話休題して外部磁場との相互作用を考える。

局在スピンと外部磁場との相互作用は、

(5.29)

H_B=\int\frac{d^3r}{a^3}\hbar\gamma \bm B\cdot\bm S

エネルギーは \bm S と \bm B とが同じ向きを向く時に最大となる。

これは、電子の電荷が負であるために磁化 \bm M=-\frac{\hbar\gamma}{a^3}\bm S が局在スピン \bm S と反対方向を向くためである。 局在スピン \bm S と \bm B とが同じ向きを向く時、 磁化 \bm M と \bm B とは逆向きになり、エネルギーが高くなる。

\bm B//\bm e_z かつ S_z=S\cos\theta 、そして (5.25) を用いれば、

\bm B\cdot \bm S=BS\cos\theta=BS\tanh\frac{z-X(t)}{\lambda}

より、

(5.29)

H_B&=\hbar\gamma BS\int\frac{d^3r}{a^3}\tanh\frac{z-X(t)}{\lambda}\\ &=\frac{\hbar\gamma}{a^3} BSA\int dz\tanh\frac{z-X(t)}{\lambda}\\

z に関する積分範囲はこれまで (-\infty,\infty) とされていて、 それを使って部分積分なんかもしてきた気がするのだけれど、ここでは突如 [-L/2,L/2] として系のサイズ L を考えてしまう。 L\gg\lambda である限り問題は起きなさそうだけれど、話の流れとしてはちょっと乱暴。。。

(5.30)

H_B&=\frac{\hbar\gamma}{a^3} BSA\int_{-L/2}^{L/2} dz\tanh\frac{z-X(t)}{\lambda}\\ &=\frac{\hbar\gamma}{a^3} BSA\int_{-L/2}^{L/2} dz\lambda\frac{\frac{1}{\lambda}\sinh\frac{z-X(t)}{\lambda}}{\cosh\frac{z-X(t)}{\lambda}}\\ &=\frac{\hbar\gamma\lambda}{a^3} BSA\int_{-L/2}^{L/2} dz\frac{\left(\cosh\frac{z-X(t)}{\lambda}\right)'}{\cosh\frac{z-X(t)}{\lambda}}\\ &=\frac{\hbar\gamma\lambda}{a^3} BSA\left[\ln \big(\cosh\frac{z-X(t)}{\lambda}\big)\right]_{-L/2}^{L/2}\\ &=\frac{\hbar\gamma\lambda}{a^3} BSA\left[\ln \big(e^{\frac{z-X(t)}{\lambda}}+e^{-\frac{z-X(t)}{\lambda}}\big)-\ln 2\right]_{-L/2}^{L/2}\\ &=\frac{\hbar\gamma\lambda}{a^3} BSA\left[\ln \big(e^{\frac{L/2-X(t)}{\lambda}}+e^{-\frac{L/2-X(t)}{\lambda}}\big)-\ln \big(e^{\frac{-L/2-X(t)}{\lambda}}+e^{-\frac{-L/2-X(t)}{\lambda}}\big)\right]\\ &=\frac{\hbar\gamma\lambda}{a^3} BSA\ln \left[\frac{e^{\frac{L/2-X(t)}{\lambda}}+e^{-\frac{L/2-X(t)}{\lambda}}}{e^{\frac{-L/2-X(t)}{\lambda}}+e^{-\frac{-L/2-X(t)}{\lambda}}}\right]\\ &=\frac{\hbar\gamma\lambda}{a^3} BSA\ln \left[\frac{1+e^{-\frac{L-2X(t)}{\lambda}}}{\red{e^{\frac{-L}{\lambda}}+e^{\frac{2X(t)}{\lambda}}}}\right]\\ &=\frac{\hbar\gamma\lambda}{a^3} BSA\ln \left[e^{\frac{-2X(t)}{\lambda}}\frac{1+e^{-\frac{L-2X(t)}{\lambda}}}{1+e^{\frac{-L-2X(t)}{\lambda}}}\right]\\ &=\frac{\hbar\gamma\lambda}{a^3} BSA \left[\frac{-2X(t)}{\lambda}+\ln\left\{\big(1+e^{\frac{-L+2X(t)}{\lambda}}\big)\big(1-e^{\frac{-L-2X(t)}{\lambda}}+\dots\big)\right\}\right]\\ &=\frac{\hbar\gamma\lambda}{a^3} BSA \left[\frac{-2X(t)}{\lambda}+\ln\left\{\big(1+e^{\frac{-L}{\lambda}}(e^{\frac{2X(t)}{\lambda}}-e^{\frac{-2X(t)}{\lambda}})-\dots\big)\right\}\right]\\ &=\frac{\hbar\gamma\lambda}{a^3} BSA \left[\frac{-2X(t)}{\lambda}+e^{\frac{-L}{\lambda}}(e^{\frac{2X(t)}{\lambda}}-e^{\frac{-2X(t)}{\lambda}})+\dots\right]\\ &=-\hbar N_wS\gamma B\frac{X(t)}{\lambda}+O(e^\frac{-L}{\lambda})

途中赤にした部分、教科書の２行目に当たるところは分母がおかしいと思う。
それと最終結果で教科書には const. という項が出てくるけれど、 そんな項は現れない気がする？
（ X=0 と置けば \tanh\frac{z}{\lambda} は奇関数で、 積分値がゼロになるのは明らか）

この結果から、容易軸方向の磁場は磁壁にポテンシャル勾配、すなわち力を与えることが分かる。

・・・実はこの内容は、もっとずっと簡単に得られる話。
磁壁が \Delta X 動けば、 \frac{A\Delta X}{a^3} 分のスピンが向きを変えるので、 この値に \hbar \gamma B を掛ければ、他に定数項が生じる可能性だけ残して (5.30) が得られる。上記のようにちゃんと積分すると、「定数項が生じないこと」を 確認できるが、const. を付けてしまうと元も子もない感じが。

O(e^\frac{-L}{\lambda}) は系が有限な長さを持っているための効果で、 L が十分に長く、端で \bm S が完全に容易軸方向を向いていると見なせる限り無視できる。

これを自由な磁壁のラグランジアン (5.23) に加えることで、

(5.31)

L_w^B\equiv L_w^{(0)}-H_B=\frac{\hbar N_wS}{\lambda}\left(\dot X\phi_0+\gamma BX\right)

このラグランジアンから緩和入りの運動方程式を求めると、

(5.32)

\frac{\red\PD}{\red\PD X}L_w^B-\frac{d}{dt}\frac{\red\PD}{\red\PD \dot X}L_w^B=-\frac{\red\PD W_S}{\red\PD\dot X}

\frac{\hbar N_wS}{\lambda}\left(\gamma B-\dot\phi_0\right)=\frac{\alpha N_w\hbar S}{2} \frac{2\dot X}{\lambda^2}

\gamma B-\dot\phi_0=\alpha \frac{\dot X}{\lambda}

\frac{\red\PD}{\red\PD \phi_0}L_w^B-\frac{d}{dt}\frac{\red\PD}{\red\PD \dot \phi_0}L_w^B=-\frac{\red\PD W_S}{\red\PD\dot \phi_0}

\frac{\hbar N_wS}{\lambda}\dot X=\frac{\alpha N_w\hbar S}{2} 2\dot\phi_0

\frac{1}{\lambda}\dot X=\alpha\dot\phi_0

（ X や \phi は単なる変数なので、汎関数微分で書くのはおかしい）
これを \dot X,\dot \phi_0 について解けば、

(5.33)

\dot X/\lambda=\alpha(-\alpha\dot X/\lambda+\gamma B)

\frac{\dot X}{\lambda}=\frac{\alpha}{1+\alpha^2}\gamma B

\dot\phi_0+\alpha(\alpha\dot\phi_0)=\gamma B

\dot\phi_0=\frac{1}{1+\alpha^2}\gamma B

として、 X,\phi_0 ともに等速度運動を行うことが分かる。
特にこのとき、運動の速度は磁場由来の外力と摩擦力とが釣り合う条件で決まっており、 摩擦力が本質的な役割を担っている。

等速運動が唯一の解？？？†

速度に比例する散逸項を持つ運動を普通に思い浮かべると、 始め静止していた物体に外力が掛かると徐々に速度を増して、 最終的に外力と摩擦力が釣り合う速度に漸近することになる。

しかしここで出てきた解はそのような加速度運動を許しておらず、 「常に」一定速度で動くという解になっている。

たとえ時刻ゼロで磁壁が静止していたとしても、 外場を与えた瞬間に等速運動するというのがこの解。

そんなことがあり得るだろうか？

そんなことがあり得る理由は、 以下に見るとおり、上で求めた解は外場の中で磁壁が回転しながら、 緩和項のおかげで徐々に徐々に平行移動するという運動を表しており、 緩和項自体が運動の原動力となっているところにある。

この状況は外場による運動を緩和項が抑えているという通常の状況とは大きく異なっている。

5-5 で見るとおり、今の系に困難軸異方性を持ち込んだ場合には 磁壁が「質量」を持つように振る舞うが、 容易軸異方性のみを考えた今の系では磁壁は質量を持つような振る舞いを見せないということになる。

摩擦力の役割†

摩擦力に対する \dot X および \dot \phi_0 の関係は、

外部磁場と摩擦.png

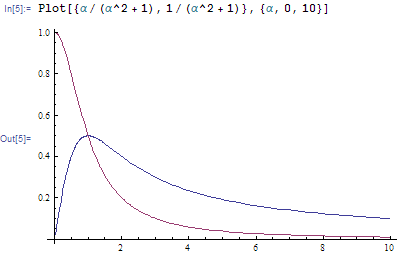
となっていて、

移動速度 \dot X の摩擦係数依存性は

  • 摩擦がないとき速度 0
  • \alpha=1 で最大値 \frac{1}{2}\lambda\gamma B
  • その後 1/\alpha で減衰する
  • 実際の系では \alpha\ll 1 なので、摩擦が大きければ大きいほど磁壁の移動速度が上がることになる

ちょっと考えると摩擦がないときに速度が 0 になるのが不思議だが・・・
\dot X が小さくなる代わりに \dot \phi が大きくなっているところが重要なはず。

すなわち、摩擦が小さいときには「平行移動」が小さい代わりに「回転」が速くなる。

平行移動すると系はポテンシャルからエネルギーを得るが、 等速運動をしているときには得たエネルギーとちょうどおなじだけ散逸でエネルギーを失う。

摩擦が小さいときには平行移動の速度が小さくても、 その分ポテンシャルから得るエネルギーは小さく、 また、回転運動による散逸は大きくなるため、つじつまが合う。

試みに、単位時間あたりに散逸するエネルギーを求めてみよう。

抵抗力は散逸関数の微分に変位速度を掛けて求まる。、

\frac{\PD W_S}{\PD \dot X}\dot X+\frac{\PD W_S}{\PD \dot\phi_0}\dot\phi_0&= \alpha N_w\hbar S\left(\frac{\dot X^2}{\lambda^2}+\dot\phi_0^2\right)\\ &=N_w\hbar S(\gamma B)^2\left[\alpha\left(\frac{\alpha}{1+\alpha^2}\right)^2+\alpha\left(\frac{1}{1+\alpha^2}\right)^2\right]\\ &=N_w\hbar S(\gamma B)^2\frac{\alpha}{1+\alpha^2}

一方、磁壁が動くことにより系が得るエネルギーは

-\frac{\PD H_B}{\PD X}\dot X &=\hbar N_wS\gamma B\frac{\dot X}{\lambda}\\ &=\hbar N_wS(\gamma B)^2\frac{\alpha}{1+\alpha^2}\\

等速運動で運動エネルギーが変化しないのは、このように両者が釣り合っているため。

\dot X 由来と \dot\phi_0 由来、また、合計の散逸の大きさを比べてみると 次のようになる。

外部磁場と摩擦2.png

\alpha がゼロに近いところでは、速度が遅くなる分、 ポテンシャルから得られるエネルギー（合計の散逸に等しい）は小さくなる。

そこでは \dot X 由来の散逸に比べて \dot\phi_0 由来の散逸が非常に大きくなるため、 \alpha\rightarrow 0 の極限では並進速度が得られず磁壁は停止する。

なぜ摩擦が無い時「回転」するのか？†

(4.14) でやったように、個々のスピンの運動は、 スピン位置での有効磁場の周りを歳差運動するか、 あるいは有効磁場の方向かその逆を向いて静止するかである。

静止磁壁構造が静止しているのは、すべてのスピンの位置で、 それぞれのスピンが感じる有効磁場の方向にスピンが静止しているため。

そこに外場を掛けると、磁壁から遠いところではスピンは容易軸方向、 すなわち外場方向と平行・反平行なので静止したままだが、 磁壁内部では有効磁場の方向が変化してしまうため、 それぞれのスピンは有効磁場の周りを回転する回転運動を始める。

摩擦があるおかげで平行移動が生じる†

摩擦が無ければこの回転は止まることなく、一定の周期で回り続けることになり、 磁壁位置はいつまで経っても変わらない。

しかし摩擦があると、スピンは徐々に回転運動量を減らして有効磁場の方向に揃っていき、 その分だけ磁壁が平行移動する。

その意味で、今考えている系では磁壁の平行移動は摩擦があって初めて生じる現象であると言える。

上で見たように摩擦力が大きい極限 ( \alpha>1 ) では平行移動の摩擦力によって速度が抑えられることになるが、 現実にそこまで大きな摩擦力が生じることはないため、 通常、摩擦が大きければ大きいほど平行移動速度が速くなると考えて良い（のだと思う）。

教科書では「緩和項 \alpha の存在が本質的となっている」とさらっと書いてあるが、 「緩和項がなければ平行移動は生じない」という意味と読み取りたいところ。

(5.31) はどこから来たのだっけ？†

&L_w^B\equiv L_w^{(0)}-H_B=\frac{\hbar N_wS}{2\lambda}\left(\red{\dot X\phi_0-X\dot\phi_0}+2\gamma BX\right)\\ &\frac{\red\PD}{\red\PD X}L_w^B-\frac{d}{dt}\frac{\red\PD}{\red\PD \dot X}L_w^B=-\frac{\red\PD W_S}{\red\PD\dot X}\\ &\frac{\hbar N_wS}{2\lambda}\left(-\dot\phi_0+2\gamma B-\dot\phi_0\right)=\frac{\alpha N_w\hbar S}{2} \frac{2\dot X}{\lambda^2}\\ &\gamma B-\dot\phi_0=\alpha \frac{\dot X}{\lambda}\\ &\frac{\hbar N_wS}{\lambda}\left(\gamma B-\dot\phi_0\right)=\frac{\alpha N_w\hbar S}{2} \frac{2\dot X}{\lambda^2}\\ &\frac{\red\PD}{\red\PD \phi_0}L_w^B-\frac{d}{dt}\frac{\red\PD}{\red\PD \dot \phi_0}L_w^B=-\frac{\red\PD W_S}{\red\PD\dot \phi_0}\\ &\frac{\hbar N_wS}{2\lambda}\left(\dot X+\dot X\right)=\frac{\alpha N_w\hbar S}{2} 2\dot\phi_0\\ &\frac{\dot X}{\lambda}=\alpha\dot\phi_0\\

ここは問題ないみたい。

質問・コメント†




添付ファイル: file外部磁場と摩擦2.png 1284件 [詳細] file外部磁場と摩擦.png 1256件 [詳細]
Counter: 6397 (from 2010/06/03), today: 3, yesterday: 3